基于过期信道状态信息的无线隐蔽通信性能研究
马煜
(陕西中医药大学信息化建设管理处,陕西咸阳 712046)
隐蔽通信[1-2]作为一种新的安全范式,不同于传统加密技术或物理层安全只保护传输内容,其还保护了传输过程本身[3-5]。随着物联网的蓬勃发展[6-7],最近的研究者们探索了更复杂网络级通信系统下的隐蔽性能。当通信场景中存在多对用户时,用户之间不可避免的会产生干扰,这时提升隐蔽性能的最好做法是将干扰视为噪声[8-9]。为此有学者提出识别网络中的最佳路径的算法,进而实现最大隐蔽吞吐量或最小端到端延迟[10-11]。
目前,关于隐蔽通信的理论研究均基于一个理想的假设,即各通信节点可以获得完美的信道状态信息[12](Channel State Information,CSI)。由于CSI 提取过程的复杂性,各通信节点往往会得到一个过期的CSI[13-14]。该文研究了过期CSI 下两跳隐蔽通信系统在经典速率控制方案(Rate-Control Transmission,RCT)下的传输隐蔽通信性能。
1 无线隐蔽通信性能分析模型
该文考虑了一种由源节点、放大转发中继节点和目的节点组成的无线两跳中继传输模型。其中,每个节点只配备一根天线并且在半双工的模式下运转,因此,同一个节点同一时刻只能发送或者是接收信息。另外,假设源节点与目的节点之间的距离较远且信道衰落严重,所以源节点必须借助中继节点来转发公开信息。然而中继节点在转发公开信息的同时,还私自向目的节点发送隐蔽信息,因此中继节点发送隐蔽信息时必须对抗来自源节点的监测。考虑到对隐蔽传输最苛刻的情况,即源节点这个监测者可以采用最优检测阈值使得监测错误概率最低。因此,该文分别分析了速率控制方案下的隐蔽性能,推导了RCT方案下检测错误率[15](Detection Error Probability,DEP)和隐蔽速率[16](Covert Rate,CR)的闭式表达式。
1.1 传输条件分析
当事件A0发生时,为了保证合法公开信息xs的传输速率Ra固定,中继节点在满足最大传输功率的约束下,需要调整xs的传输功率使信道容量Ca等于传输速率Ra。因为假如Ca大于传输速率,多余的容量将被闲置,这是对能量的一种浪费;假如Ca小于Ra,便会发生传输中断。
在两跳传输系统中,Ca与目的节点处SINR 的关系如式(1)所示:
1.2 速率控制方案下成功传输隐蔽信息的概率
1.3 检测错误概率
为了得到DEP 的闭式表达式,首先推导了如下引理描述误报率和漏检率。
引理1:在中继节点采用RCT 方案的情况下,源节点处设置不同的检测阈值对应的误报率如式(4)所示:
漏检率公式(5)所示:
引理2:对于该文所考虑的过期CSI 系统,源节点处的DEP 如式(6)所示:
源节点作为监测者,需要设置一个最优的检测阈值τ使得DEP 最小。假设源节点可以找到并采用了最优的检测阈值,这对中继节点处要进行的隐蔽通信来说是最坏的情况,为此提出如下定理来描述最小DEP。
引理3:当源节点处采用最优检测阈值τ*时,对应的最小DEP 如式(7)所示:
1.4 隐蔽速率
隐蔽速率(Covert Rate,CR)是在较长一段时间内,从中继节点到目的节点进行隐蔽通信的平均速率,而非瞬时值。CR 是衡量隐蔽通信性能的一项重要指标。
定理3:对于RCT 方案,在考虑过期CSI 的情况下,中继节点可以实现的CR 如式(8)所示:
只有当事件A1发生时,中继节点才传输隐蔽信息,所以计算CR 时,需要考虑那些所有保证事件A1发生的信道情况。
1.5 隐蔽性约束下的最优隐蔽速率
检测阈值τ和设计参数Qc是DEP 和CR 的两个重要影响因素,其中,τ由源节点决定,Qc由中继节点决定。中继节点希望通过调整Qc使得CR 尽量大,但是提高CR 的代价增加了通信过程暴露的可能性,即降低了DEP。采用RCT 方案进行隐蔽传输,考虑对于隐蔽传输最差的情况,隐蔽通信在速率方面满足一定条件时,即CR 大于给定阈值ε时,需要设置最优的Qc来得到最大DEP,如式(9)所示:
1.6 隐蔽速率约束下的最优隐蔽性
可以看出CR 不是Qc的单调函数,CR 随着Qc的增加而增加,但是随着Qc的增加而减小。采用RCT 方案进行隐蔽传输,考虑对于隐蔽传输最差的情况,在隐蔽性满足一定条件时,即DEP 大于给定阈值ε时,设置最优的Qc来得到最大的CR,如式(10)所示:
其中,约束条件表示最优检测阈值对应的最小DEP 大于给定阈值。类似地,式(10)所描述的最优化问题也可以通过数值搜索的方法求解,并将求得的最优设计参数Qc记作最大隐蔽速率记作CR*。
2 实验设计与评估
2.1 实验参数
在实验设计中,仿真过程中各参数默认值如下:η=0.5,信道增益系数hsr=1,hrd=1,源节点的AWGN噪声=0 dB,源节点的发射功率Ps=13 dB,信道无关误差ωsr=0.05,ωrd=0.05。
2.2 RCT方案下的检测错误概率分析
该节探索了在RCT 方案下检测阈值对DEP 的影响,其中,在RCT 方案下不同的CSI 相关系数和中继节点设计参数配置下,DEP 随检测阈值的变化如图1所示。
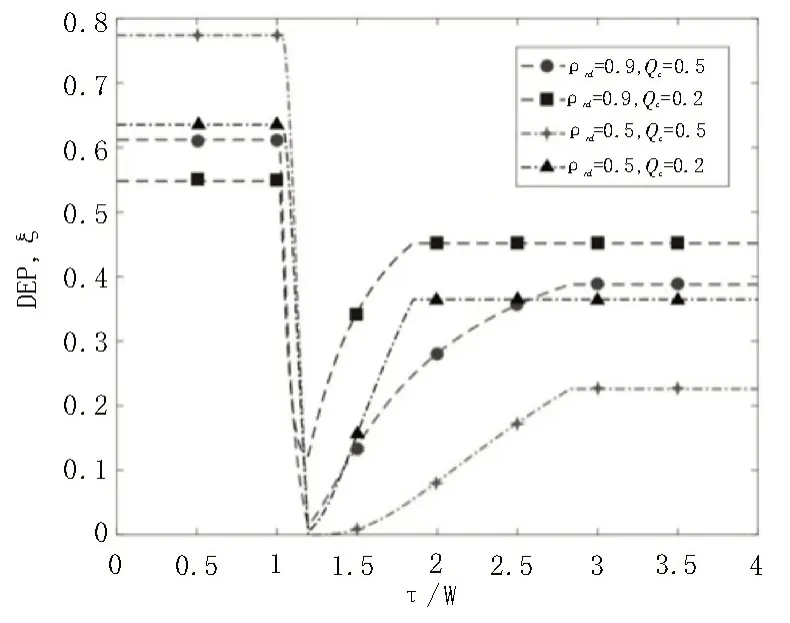
图1 DEP随检测阈值的变化
可以看到在给定的CSI 相关系数和中继节点设计参数配置下,DEP 的曲线分割为4 段。比如圆点标注这条ρrd=0.9,QC=0.5 的曲线,当τ∈[0,1]时≥τ,ξ是一个定值,对应第一个分段;当τ∈[1,1.4] 时,μ1≥τ>,ξ随着τ的增加而减小,对应第二个分段;当τ∈(1.4,2.8]时,μ2≥τ>μ1,ξ随着τ的增加而增加,对应第三个分段;当τ>2.8 时,τ>μ2,ξ是一个定值,对应第四个分段。注意到当τ∈(1,1.4]时,ξ有一个最小值,其实无论ρrd和Qc取值如何,当μ2≥τ>μ1时,ξ总是存在一个最小值。
为了探究合法信息的传输速率Ra对最小DEP的影响,绘制在RCT 方案下ξ*关于Ra的变化图如图2 所示。对于固定的Qc或Pc,较大的ρrd会造成较大的ξ*,这是由于较大的ρrd代表较小程度的CSI 时延,有利于中继节点去分析监测者处的配置。另一方面,对于固定的ρrd,较大的Qc或Pc会导致较小的ξ*,这是因为Qc或Pc的增大意味着隐蔽信息的传输功率增大,导致隐蔽通信过程更容易暴露给监测者。
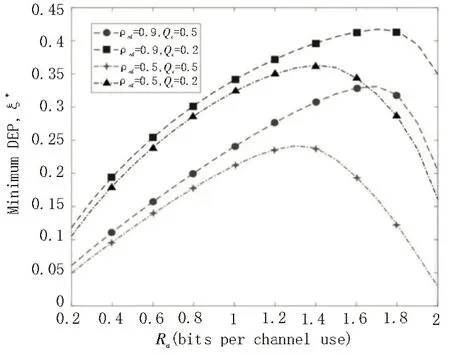
图2 RCT方案下的最小检测错误概率
2.3 RCT方案下的隐蔽速率分析
以上是站在监测者的角度对隐蔽性进行了数值分析,下文将站在隐蔽传输者即中继节点的角度分析隐蔽传输速率。如图3 所示,随着Pc的增加,CR 先增加到一个最大值,然后减小。这是因为CR 是隐蔽信息的瞬时传输速率CR 和成功传输概率的综合测度,Pc对CR 的影响是两方面的。一方面,较大的Pc导致较大的CR;另一方面,Pc越大,越小。这意味着CR和之间的权衡导致了CR的单峰行为。

图3 RCT方案下的隐蔽速率
3 结束语
该文分析了各通信节点在只能得到过期CSI 的情况下,两跳通信系统的隐蔽性能。通过建立系统模型、推导包括DEP 和CR 的隐蔽性能的精确表达式,建立了具有代表性的数学理论模型来刻画过期CSI对隐蔽性能的影响。在此基础上进一步提出RCT方案,并解决了具有实际意义的问题,以揭示隐蔽性和隐蔽传输速率之间的关系。

