边破坏对多智能体系统能控性的影响
肖朋朋,纪志坚
(1.青岛大学 自动化学院,山东青岛 266071;2.山东省工业控制重点实验室,山东青岛 266071)
随着社会的发展和科技的进步,国内外众多学者对多智能体系统的研究逐步深入,网络拓扑为研究多智能体系统提供了一种分析工具。近年来,多智能体系统不仅在控制领域,在无人机编队等领域[1-8]也进行了深入研究。
能控性概念是上个世纪60 年代由卡尔曼首次提出,2004 年能控性的概念被引入到多智能体的研究当中。近些年,多智能体系统研究取得了显著的成就,如自适应控制[9-11]、博弈控制[12-14]、切换系统[15]等都已应用于多智能体系统中。一类边集失效对复杂网络能控性的影响已经有过讨论[16],但不同类型的边失效对多智能体系统能控性的影响,以及对拉普拉斯矩阵秩的影响,目前还没有给出确切的结论。因此,为了解决此问题,将系统中的边进行分类,并从理论层面给出不同类型的边失效对系统能控性影响的确切结论。文中提出了一种边的分类方式,将多智能体系统中的边分为三种类型,边组合分为四种组合类型,并提供了一种辨识边类型的算法,给出了不同类型的边失效后系统能控性的变化规律。同时,为了保证边失效后的系统是能控的,给出了领导者的选择方法,最后通过实例验证了结论。
1 预备知识
1.1 图论知识
对于含有N个节点的多智能体系统G(A)=(V,E,A),其中V={v1,v2,…,vN} 表示系统的节点集,E={e1,e2,…,eN}表示系统的边集,A=[aij]∈RN×N表示加权邻接矩阵,aij表示节点j对节点i的影响程度,若无特殊说明,aij=1。文中不考虑存在自环的情况,即(vi,vi)∉E。Ni={j∈V∣(j,i)∈E}表示节点i的邻居集合。在有向图G中,对于不同的节点i、j,都有一条从i开始到j结束的定向路径,则称图G为强连通图。di=||Ni表示节点i的度,有向图G的度矩阵为D(G)=diag(d1,d2,…,dN)。拉普拉斯矩阵(Laplacian matrix)是相较于度矩阵的另一种表达图中顶点关系的矩阵,拉普拉斯矩阵可以用L(G)=D(G)-A(G)表示。
1.2 数学符号
R表示实数集,Rn表示n维实向量空间。XY表示属于X但不属于Y的集合,I为单位矩阵,O表示文中合适维度的零矩阵,ϕ表示空集。
1.3 系统模型
其中,L∈RN×N为拉普拉斯矩阵,B∈RN×P为外部控制输入矩阵。
对于线性时不变系统(1),若存在一个分段连续的输入u(t)能够在有限时间[t0,tf]内使得系统从任意初始状态转移到任意终止状态,则称此系统的状态是完全能控的。可以通过能控性判据来判断系统是否是能控的,即系统完全能控的充分必要条件是矩阵C=[B,LB,…LN-1B] 满秩,即rankC=N。此时,我们称该系统是完全能控的。
定义1对于有向图G的一个子图G′,如果G′为单向强连通环图,且对于任意j∈V/V′,i∈V′,都有(i,j)∉E,强连通子图G′整体只有单个输入,这种结构称为InSCC。在文中将InSCC 结构外且没有入度的节点作为初始节点,即节点1 为初始节点,如图1所示。
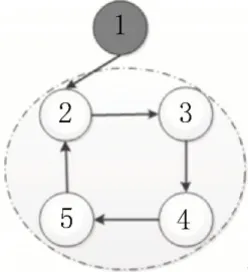
图1 InSCC结构
2 多智能体系统中边的分类辨识
在含有InSCC 结构的多智能体系统中,边失效后,系统的能控性怎样变化以及如何再次选择领导者保证系统能控,都是十分有意义的问题。
2.1 多智能体系统中边的分类
含有InSCC 结构的多智能体系统通常由节点和有向边组成,其中节点存在三种类型,边也存在三种类型。
2.1.1 边的分类
类型1:如图2(a)所示,对于多智能体系统中的一条边,如边(v1→v2),如果和初始节点相连,则这条边为关键边,记作xK。
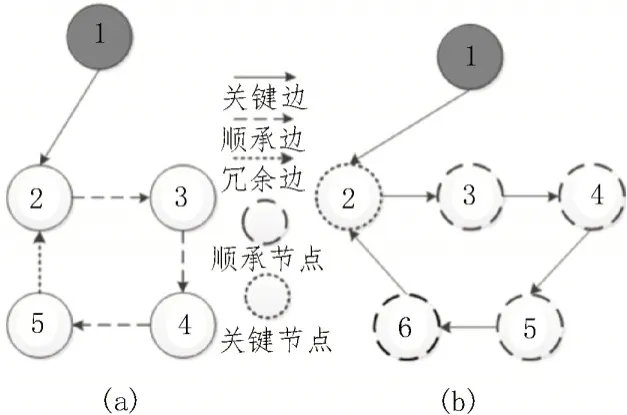
图2 节点和边在网络中的关系
类型2:如图2(a)所示,对于多智能体系统中的一条边,如边(v2→v3)或(v3→v4),如果一条边由关键节点指向顺承节点或者由顺承节点指向顺承节点,则这条边为顺承边,记作xF。
类型3:如图2(a)所示,对于系统中的一条边,如边(v6→v2),如果一条边由顺承节点指向关键节点,则这条边为冗余边,记作xR。
2.1.2 节点分类
类型1:如图2(b)所示,对于多智能体系统中的一个节点,独立于InSCC 结构外且没有入度的节点作为初始节点,如节点1。
类型2:如图2(b)所示,对于多智能体系统中的一个节点,和初始节点相连的边指向的节点为关键节点,如节点2。
类型3:如图2(b)所示,对于多智能体系统中的一个节点,顺承边指向的节点为顺承节点,如节点3、4、5 和6。
2.2 多智能体系统中边组合失效类型
根据节点和边的类型,对不同边的组合进行分类,每个组合有且仅有两条边。
类型1:关键边和顺承边遭到破坏而失效,则失效组合为关键边-顺承边组合,记xK-F。
类型2:关键边和冗余边遭到破坏而失效,则失效组合为关键边-冗余边组合,记xK-R。
类型3:顺承边和顺承边遭到破坏而失效,则失效组合为顺承边-顺承边组合,记xF-F。
类型4:顺承边和冗余边遭到破坏而失效,则失效组合为顺承边-冗余边组合,记xF-R。
2.3 边组合的辨识算法
为了更好地探究边失效对多智能体系统能控性的影响,需要找出多智能体系统中边的类型,下面给出多智能体系统中边的辨识算法,具体步骤如下:
Step1:遍历多智能体系统中的所有节点,如果存在一条边(vi→vj),其中节点vi为初始节点,那么由节点vi指出的边为关键边。
Step2:遍历多智能体系统中的所有节点,如果存在一条边(vi→vj),其中节点vi为关键节点或者为顺承节点,节点vj为顺承节点,那么由节点vi指向节点vj的边为顺承边。
Step3:遍历多智能体系统中的所有节点,如果存在一条边(vi→vj),其中节点vi为顺承节点,节点vj为关键节点,那么由节点vi指向节点vj的边为冗余边。
Step4:搜寻第一条与初始节点相连接的边为关键边,如果第二条边是从关键节点或顺承节点vj出发,到顺承节点vj+1结束,边(vj→vj+1)为顺承边,则找出关键边-顺承边组合xK-F,否则进行下一步。
Step5:搜寻第一条与初始节点相连接的边为关键边,如果第二条边是从顺承节点vj出发,到关键节点vj+1结束,边(vj→vj+1)为冗余边,找出关键边-冗余边组合xK-R。
Step6:搜寻第一条边从关键节点或顺承节点vi出发,到顺承节点vi+1结束,边(vi→vi+1)为顺承边,如果第二条边是从关键节点或顺承节点vj出发,到顺承节点vj+1结束,边(vj→vj+1) 为顺承边,那么边(vi→vi+1)与边(vj→vj+1)的组合为顺承边-顺承边组合xF-F,否则进行下一步。
Step7:搜寻第一条边从关键节点或顺承节点vi出发,到顺承节点vi+1结束,边(vi→vi+1)为顺承边,如果第二条边是从顺承节点vj出发,到关键节点vj+1结束,边(vj→vj+1)为冗余边,那么边(vi→vi+1)与边(vj→vj+1)的组合为顺承边-冗余边组合xF-R。
3 边失效对多智能体系统能控性影响
定理1 对于含有N个节点的多智能体系统,其中含有n个不同的InSCC 结构。
1)当失效n条关键边时,多智能体系统的能控子空间维数降低。rank(LK)=N-n-1,LK为丢失关键边后的拉普拉斯矩阵。保证丢失n条关键边后的多智能体系统是能控的,需要选择初始节点和n个关键节点为领导者。
2)当失效n条顺承边时,多智能体系统的能控子空间维数降低。其中每个InSCC 结构失去一条顺承边,rank(LF)=N-n-1,LF为丢失顺承边后的拉普拉斯矩阵。保证丢失n条顺承边后的多智能体系统是能控的,需要对初始节点和n个失效顺承边指向的顺承节点施加外部控制输入。
3)当失效n条冗余边时,多智能体系统的能控性保持不变,对应的拉普拉斯矩阵LR的秩不变。当选择初始节点为领导者时,多智能体系统能控性保持不变。
证明:1)当n条关键边失效时,其所对应的拉普拉斯矩阵为:
因为系统含有n个不同的InSCC,所以矩阵LKi的维数不相同。接下来计算在矩阵LK的特征值中零特征值的重数:
其中,LK0=0,每个|λI-LKi|中存在一个特征值λ=0,所以在LK的特征值中,λ=0 的重数为n+1,即rank(LK)=N-n-1。
当选择初始节点为领导者时,关键边失效后的系统存在N-1 个输入不可达节点,系统的能控子空间维数降低。根据InSCC 结构的特性,当多智能体系统中所有的节点输入可达时,系统能控。保证丢失n条关键边后的多智能体系统是能控的,选择输入矩阵B=[bK0,bK1,…,bKn],其 中bK0=[1,0,…,0]T,bKi=[0,…,?,…,?]T,bKi∈RN×1,i∈{1,2,…,n} 。当在关键节点施加外部控制时,?=1,否则?=0,此时丢失关键边后的系统所有节点是输入可达的,系统能控。
2)当n条顺承边失效时,其中每个InSCC 结构失去一条顺承边。根据拉普拉斯矩阵行和为零的性质,拉普拉斯矩阵LF中出现n+1 个全零行,丢失n条顺承边后的拉普拉斯矩阵LF的秩减少n,因此有rank(LF)=N-n-1。保证丢失n条顺承边后的多智能体系统是能控的,则需要选择输入矩阵B=[bF0,bF1,…,bFn],其中bF0=[1,0,…,0]T,bFi=[0,…,*,…,*]T,bFi∈RN×1,i∈{1,2,…,n} 。当对失效顺承边指向的顺承节点施加外部控制输入时,*=1,否则*=0,此时系统能控。
3)当n条冗余边失效时,拉普拉斯矩阵LR中仍有N-1 线性无关的行向量,LR与冗余边失效前的拉普拉斯矩阵具有相同的秩。当选择初始节点为领导者时,系统中不存在输入不可达节点。因此,冗余边丢失前后多智能体系统能控性保持不变。
定理2对于一个含有N个节点的多智能体系统,其中含有n个不同InSCC 结构,InSCC 结构中节点数k≥3 。当丢失n组顺承边—顺承边组合(xF-F)时,每个InSCC 中丢失一组xF-F,多智能体系统的能控子空间维数降低。rank(LF-F)=N-2n-1,LF-F为丢失xF-F后的拉普拉斯矩阵。保证丢失n组xF-F后系统能控,则对初始节点和失效顺承边指向的顺承节点施加外部控制输入。
证明:对于只含有n个不同InSCC 的多智能体系统,InSCC 结构中节点数k≥3。当n组边组合xF-F失效时,其中每个InSCC 结构失去一组xF-F,根据拉普拉斯矩阵行和为零的性质,拉普拉斯矩阵LF-F中出现2n+1 个全零行。在LF-F的特征值中,特征值λ=0 的重数为2n+1,rank(LF-F)=N-2n-1。当选择初始节点为领导者时,边组合xF-F失效后的多智能体系统存在输入不可达节点,多智能体系统的能控子空间维数降低。保证丢失n条边组合xF-F后的多智能体系统是能控的,则需要选择输入矩阵B=[bF0,bF1,…,bF2n],其 中bF0=[1,0,…,0]T,bFi=[0,…,*,…,*]T,bFi∈RN×1,i∈{1,2,…,2n}。当对失效顺承边指向的顺承节点施加外部控制输入时,*=1,否则*=0,此时系统能控。
4 实例验证
图3(a)所示为只含有一个InSCC 的多智能体系统,系统的拉普拉斯矩阵为:

图3 只含有一个InSCC的多智能体系统中不同类型边失效
rank(L)=5。
1)当丢失一条关键边后,如图3(b)所示,系统的拉普拉斯矩阵为:
rank(LK)=4,关键边失效后系统的拉普拉斯矩阵的秩减少1。保证丢失关键边后的系统是能控的,则需要选择初始节点和关键节点为领导者,即选择输入矩阵BK,此时,根据系统能控性判据可知系统能控。
2)当丢失一条顺承边后,如图3(c)所示,系统的拉普拉斯矩阵为:
rank(LF)=4,顺承边失效后多智能体系统的拉普拉斯矩阵的秩减少1。保证丢失顺承边后的多智能体系统是能控的,则需要对初始节点和失效顺承边指向的那个顺承节点施加外部控制输入,即选择输入矩阵BF,此时,根据系统能控性判据可知系统能控。
3)当丢失1 条冗余边后,如图3(d)所示,拉普拉斯矩阵LR为:
其中,存在五个线性无关的行向量,因此LR与冗余边失效前的拉普拉斯矩阵L具有相同的秩。当选择初始节点为领导者时,系统中不存在输入不可达节点,因此,冗余边丢失前后多智能体系统能控性保持不变。
5 结论
文中研究了只含有InSCC 的多智能体系统在遭受攻击或破坏后,不同类型的边失效对网络能控性的影响。当关键边和顺承边失效时,系统拉普拉斯矩阵的秩减少,多智能体系统的能控子空间维数降低;当冗余边失效时,系统拉普拉斯矩阵的秩不发生改变,多智能体系统的能控性保持不变;当边组合xF-F失效时,系统拉普拉斯矩阵的秩减少,多智能体系统的能控子空间维数降低。同时,为了保证不同类型边以及边组合失效后的多智能体系统是能控的,给出了领导者的选择方法。

