基于改进FCM 算法的电力数据异常检测方法

王 璞，谢晓娜

（1.国能大渡河流域水电开发有限公司，四川成都 610041；2.成都信息工程大学自动化学院，四川成都 610225）

电力系统中通过各种智能设备采集的数据蕴藏着许多与系统运行状态有关的信息。但是实际运行中由于受到多种环境因素干扰，数据存在一定的误差或异常，影响了系统状态估计的准确性。文献[1]指出现有电力异常数据检测方法主要是基于状态估计计算的传统方法和基于数据挖掘的非传统方法，如基于神经网络[2-4]、聚类分析[5-8]及间歇统计[9]等方法。其中，基于聚类分析的检测方法在准确度、稳定性及聚类效果方面表现较好，得到了广泛应用。文献[5]提出了一种基于改进K-means 算法的电力数据异常检测方法。文献[10]提出了一种将PFCM 算法和改进粒子群优化算法相结合的电力大数据异常检测方法。

为解决FCM 算法易受噪声数据影响及初始化敏感的问题，提出一种基于改进FCM 算法的电力异常数据检测方法。首先基于距离测度的公理化定义给出一个新的距离测度计算公式，在此基础上提出一种改进的FCM 算法，并采用萤火虫算法[11](Firefly Algorithm，FA)对FCM 算法的初始化聚类中心进行优化，再依据3σ原理提出了异常数据检测方法，最后通过对比实验，对该方法的有效性进行验证。

1 相关工作

1.1 FCM算法

FCM 是通过构建目标函数来获得数据分类结果的一种求解算法[12]。对于给定数据集X={x1,x2,…,xn}，其中xi为含有d个属性的数据对象(1 ≤i≤n)，划分数据集为c个类簇(2 ≤c≤n-1)，聚类中心为V=(v1,v2,…vc)，其优化目标函数为：

式中，μij为每个样本隶属于类簇的程度；dij为每个样本到聚类中心的欧氏距离；m为模糊指数，一般取值为2。利用拉格朗日乘子法得到隶属度μij和聚类中心vj的更新式为：

1.2 萤火虫算法

萤火虫算法(AF)受自然界中萤火虫相互吸引而移动的启发实现解空间搜索，从而得到最优解。萤火虫间相互吸引主要取决于亮度和吸引度两个因素，较亮的萤火虫吸引较暗的萤火虫向其移动，最终导致所有萤火虫都趋向最亮的萤火虫，其所在位置就是解空间中最优的位置。在FA 目标优化问题求解时，萤火虫的亮度通常直接由给定问题的目标函数决定，吸引度和位置的定义[13]如下。

定义1萤火虫i与j之间的吸引度为：

式中，β0是最大吸引度，γ是光吸收因子，rij是两只萤火虫之间的欧氏距离。

定义2萤火虫i向萤火虫j移动的位置为：

式中，si、sj分别表示萤火虫i、j在解空间所处的位置；α表示步长因子，可设为[0,1]的常数；εi为服从均匀分布的随机数。

2 新型距离测度

距离测度用于衡量各个样本之间的相似程度，包括欧氏距离、曼哈顿距离和切比雪夫距离等。其中欧氏距离只考虑数据点之间的局部一致性特征，忽略了全局一致性特征[14]，为此存在无法准确刻画现实世界中含噪数据复杂结构的问题。考虑方差是一个衡量数据集分散程度的度量，下面引入方差改进欧氏距离，在距离测度的公理化定义下，提出一种新的距离测度计算公式。

定义3给定数据集X={x1,x2,…,xn}，其距离测度需要满足以下四个基本性质：

1）非负性：d(xi,xj)≥0；

2）自反性：当且仅当xi=xj时，d(xi,xj)=0；

3）对称性：d(xi,xj)=d(xj,xi)；

4）直递性：d(xi,xk)+d(xk,xj)≥d(xi,xj)。

定义4给定数据集X={x1,x2,…,xn}，其中xi是包含d个属性的数据对象(1 ≤i≤n)，其改进的距离测度定义为：

定理1由式（6）确定的距离测度满足定义3 给出的四个公理性条件。

3 文中算法

3.1 改进目标函数

聚类利用距离度量建立相似性矩阵来计算样本之间的相似度，从而确定样本的所属类别，因此选择合适的距离度量直接影响了FCM 算法的聚类性能。通常FCM 算法选择欧氏距离，而欧氏距离无法准确刻画复杂数据结构的限制，导致FCM 算法在实际应用中处理含噪或异常值的数据集时往往无法得到较佳的聚类结果。为了增强FCM 算法的噪声鲁棒性，根据新型距离测度建立相似度矩阵，提出一种改进FCM 算法，使得目标函数不仅反映样本之间的相似程度，还反映样本集全局的分散程度，表示如下：

通过求解偏导数得到隶属度μij和聚类中心vj分别为：

由此，在目标函数最小化过程中，利用式（9）和（10）对隶属度矩阵和聚类中心进行更新，然后获得最优解，最终依据最大隶属度值确定样本其所属的类别。

3.2 引入萤火虫算法

以往FCM 算法采用梯度下降方法寻找最优解。若初始值选择不当则会使算法陷入局部最优，进而影响FCM 算法的聚类结果。考虑萤火虫算法与粒子群算法和遗传算法相比在全局寻优方面更具有优势，文中在文献[15]的基础上，利用萤火虫算法对聚类中心进行优化，然后再将所获得的聚类中心作为聚类算法初始值进行聚类。具体思路：每一只萤火虫代表一个聚类中心，它的位置向量用聚类中心矩阵来表示，利用聚类算法的目标函数给出萤火虫的亮度公式为：

可见，萤火虫亮度与目标函数成反比，萤火虫的亮度越高表明目标函数越小，则其所在位置越好。

3.3 算法描述

基于上述讨论，文中首先利用萤火虫算法寻优获得最优聚类中心，然后将其作为聚类算法的聚类中心初始值进行聚类，最终获得最优划分和聚类结果。文中算法流程图如图1 所示。

图1 算法流程图

4 实验与结果分析

4.1 加噪人工数据集的测试

图2 给出了FCM 算法、PSO-PFCM[10]算法和文中算法对含噪数据集聚类所得的隶属度，可见，对于前面300 个数据点，三种算法所得的类别划分结果与数据集的实际分布情况一致，表明三种算法都能获得数据正确的划分结果。但进一步观察，图2(c)中数据样本对归属类的隶属度值更高，反之则更低，表明文中算法的类别之间划分更加清晰，聚类效果更好；同时，后100 个噪声点的隶属度均更小，与前面数据样本的隶属度变化规律截然不同，表明噪声对文中算法聚类过程的影响极小，可以忽略噪声带来的干扰，具有更强的噪声鲁棒性。

图2 三种算法的隶属度对比

4.2 电力异常数据检测

选取某水电厂2022 年5 月的真实发电量数据进行电力异常数据检测实验，采样频率为1 次/h，共155条发电量曲线。发电机的超负荷运行或发电机振动失步等不可预知因素导致测量数据含有误差，为此，各个机组的发电量曲线分布特性各不相同。首先采用各条曲线的最大值和最小值对数据进行归一化处理，然后采用FCM 算法和文中算法将155 条发电量曲线划分为五类，提取各个类别曲线及其对应的特征曲线，结果如图3 所示。从图3 可见，文中方法提取的聚类中心曲线与发电量曲线的形态更加一致，尤其在曲线趋势变化较大时，文中算法的聚类中心幅值明显与发电量更接近。

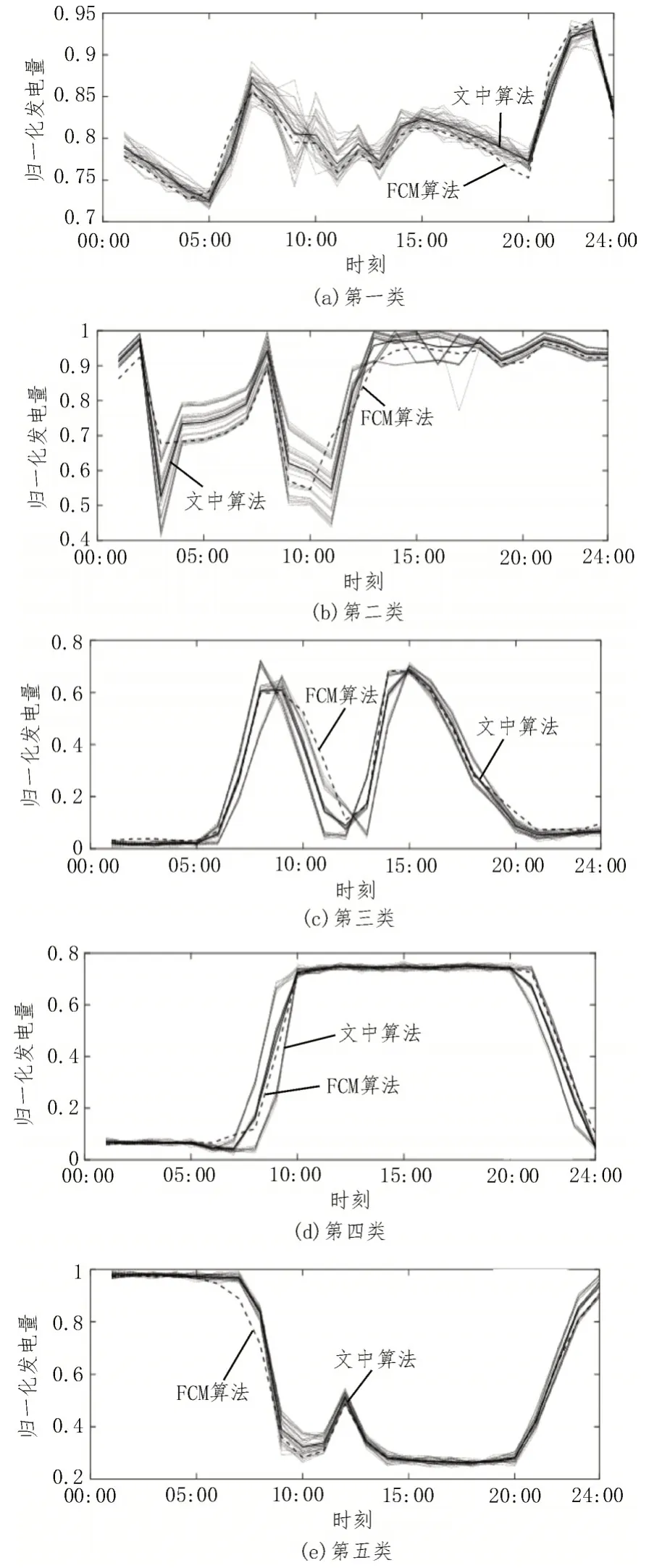
图3 两种算法聚类结果对比

在获得发电量曲线分类结果与精确提取各类特征曲线的基础上，文中依据3σ原理对异常数据进行检测，所得的部分异常数据如表1 所示。可见，该方法能够准确地检测出电力数据异常值。

表1 部分异常数据

5 结论

文中提出了一种基于改进FCM 算法的电力异常数据检测方法，克服了FCM 算法因采用欧氏距离而对噪声数据敏感和易陷入局部最优的不足。实验结果表明文中算法所获得的聚类结果类别划分更清晰、噪声鲁棒性更强，并且能够准确检测出电力异常数据。后续将利用更多聚类有效性指标来进一步分析文中算法性能，并结合特征提取方法应用于高维电力数据的异常检测。