让转化思想在数学课堂中落地生根

杨丽娟

摘 要：文章以专题“圆中角的转化”的课堂教学为例，说明如何在数学课堂教学中渗透转化思想——巧设情境，增强转化的意识；知识回顾，寻找转化的中介；解决问题，获得转化的方法。以此使学生理解转化的作用，领会数学思想的重要性。

关键词：数学思想；转化意识；转化中介；转化方法

美国教育心理学家布鲁纳指出：掌握基本的数学思想，能使数学更易于理解和记忆。数学思想是数学的灵魂和精髓，领会科学的数学思想对提升思维品质、促进终身学习具有十分重要的意义［1］。

转化也称化归，是一种常用的数学思想，是在研究和解决有关数学问题时采用某种手段将问题进行变换、转化，进而解决问题的一种思维策略。其实质就是在已有知识的基础上，利用各种变换解决问题。在教学中，教师可适当地挖掘教学内容中蕴含的转化思想，并逐步实现渗透和应用。本文以数学专题“圆中角的转化”的课堂教学为例，说明如何从增强转化意识、寻找转化中介、获得转化方法三方面着手，帮助学生理解转化思想。

一、巧设情境，增强转化意识

圆是重要的基本图形，在长期的探索与研究中，人们发现了许多圆的相关性质。同时，角是图形的重要元素，很多较为复杂的图形都涉及角。圆锥曲线是初中阶段的难点知识，学生在初次接触时容易感到困难。而圆的特征赋予角极强的活性，如果将圆中的角进行灵活转化，许多难题便能迎刃而解。教师可以在教学中创设有趣的问题情境，让学生在解决问题的过程中感受转化思想、增强转化意识。

情境引入：

如图1，在“世界杯”足球预选赛中，甲带球向对方球门PQ进攻。当他带球冲到A点时，同伴乙已经助攻冲到B点。现有两种射门方式：第一种，甲直接射门；第二种，甲将球传给乙，由乙射门。仅从射门角度考虑，应选择哪种射门方式？为什么？

分析：仅从射门角度考虑射门方式即比较∠A与∠B的大小。连接PD，根据同弧所对的圆周角相等，发现∠PDQ=∠B，而∠PDQ是△PAD的外角，∠PDQ＞∠A，于是∠B＞∠A。因此，由乙在點B处射门有利。

如果连接QC，同样可以得出答案。

设计意图：添加辅助线，就是利用同弧所对的圆周角相等，将∠B转化到∠PDQ，从而实现∠A与∠B的大小比较。这一问题情境可以让学生意识到圆内角转化的重要性，产生探究转化思想的内需。

二、知识回顾，寻找转化中介

中介是指在不同事物或同一事物内部对立两极之间起居间联系作用的部分。要进行圆中角的转化，就要寻找转化的中介。

例：如图2-1，点A、B、C在⊙O上。

问题1：你找到了哪些与⊙O有关的角？这些角之间有怎样的数量关系？

分析：利用圆心角的度数与它所对的弧的度数相等，得∠BOC=100°，利用圆周角的度数等于它所对的弧上圆心角度数的一半，得∠BAC=50°；利用等边对等角，由半径OB=OC，得∠OBC=∠OCB=40°。由此获得转化中介——半径，实现边角转化。

分析：利用同弧或等弧所对的圆周角相等，由∠BAC=50°得∠BDC=50°。由此强调转化中介——弧，说明位置变化，数量关系不变。

分析：利用圆内接四边形的对角互补，由∠BAC= 50°，得∠BEC=130°，进而得∠BEF =50°，因此∠BEF=∠BAC，说明圆内接四边形的外角等于它的内对角。由此获得转化中介——圆的内接四边形，实现圆外角与圆内角的转化。

分析：利用切线的性质，得∠OCG=∠OCH= 90°；利用余角的性质，由∠OCB=40°得∠BCH= 50°，因此∠BCH=∠BAC。由此获得转化中介——切线，实现弦切角与圆内角的转化。

设计意图：以一道操作题引出问题串，使图形由浅入深。在保证学生思维连贯的前提下，通过动手动脑，既对圆中角的相关知识进行了回顾，又探索获得了圆中角转化的中介，为利用转化思想解决数学问题做好铺垫。

三、解决问题，获得转化方法

转化的方法灵活多样，既与实际问题的内容和特点有关，也与学生的认知结构有关。对于圆中角的转化，在解决问题的过程中通过体验获得方法，不仅可以丰富经验积累，还能提升数学素养。

（一）通过热身练习，直接发现，应用转化

教师可以设计一组简单练习，直接利用转化中介解决问题，使学生加深对转化中介的掌握，巩固对圆中角的转化的理解及应用。学生经历思考、交流，认知会更深刻。

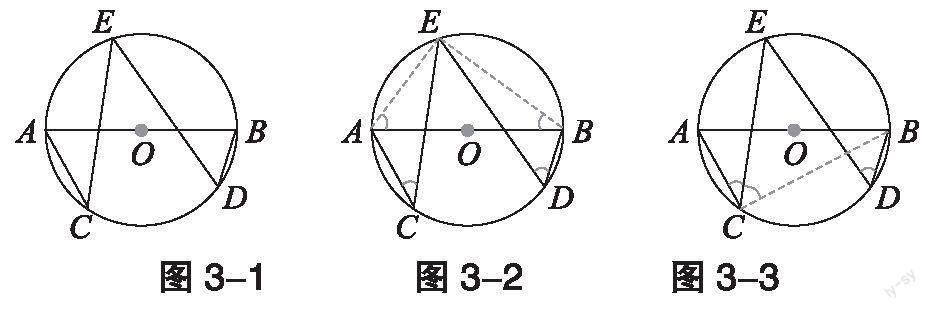
练习1：如图3-1，AB是⊙O的直径，C、D、E都是⊙O上的点，则∠C+∠D= 。

方法1——由弧看角

方法2——由角看弧

设计意图：由弧看角，直接进行圆周角之间的等量转化，学生容易想到。由角看弧，将圆周角转化到圆弧上，实现抽象到直观的转变，非常简洁。

练习2：已知四边形ABCD是⊙O的内接四边形，若∠A∶∠B∶∠C=4∶3∶5，则∠D的度数是（ ）

A.60° B.80° C.100° D.120°

设计意图：利用圆的内接四边形对角互补，求∠D的度数，直接转化到∠B。由已知条件可知∠A=80°，∠B=60°，∠C=100°，因此∠D=120°。

练习3：如图4，四边形ABCD是⊙O的内接四边形，AD与BC的延长线交于点E，BA与CD的延长线交于点F，若∠DCE=80°，∠F=25°，那么∠EDC的度数为 。

方法1：由已知条件∠DCE=80°，∠F=25°，可知∠B=55°，利用圆的内接四边形的外角等于它的内对角，则∠EDC=∠B=55°。

方法2：利用圆的内接四边形的外角等于它的内对角，由∠DCE=80°，知∠DAB=∠DCE=80°，于是∠FDA=55°，因此∠FDA的对顶角∠EDC=55°。

设计意图：两种方法都利用“圆的内接四边形的外角等于它的内对角”的性质，将圆外角转化为圆内角来解决问题。方法1综合考虑两个已知条件，思路相对简洁。

（二）借助难点突破，添线构造，获得转化

可以设计有难度的练习，引导学生利用圆中角的转化方法进行添线，构造转化中介。学生经历实践探索，对获得的数学经验进行反思，能够掌握解题策略，有效突破教学重难点。

A.120° B.130° C.140° D.150°

分析：如图5-2，连接AC，利用直径BC构造直角∠BAC。在Rt△ABC中，由三角函数可知∠B=30°，于是得到∠D=150°。

设计意图：利用直径构造直角，借助直角三角形实现边角转化。

练习5：如图6-1，PA是⊙O的切线，切点为A，PO的延长线交⊙O于点B，连接AB。若∠P=40°，则∠B的度数为（ ）

A.20° B.25° C.40° D.50°

分析：如图6-2，连接OA，利用切线PA构造直角∠PAO。在Rt△PAO中，由∠P=40°得到∠POA=50°，从而求得∠B=25°。

设计意图：利用切线构造直角，借助直角三角形的两个锐角互余，实现圆中角的转化。

练习6：如图7-1，已知AB是⊙O的直径，C为⊙O上一点，CD⊥AB于点D，E是OB上一点，CE、AG交于点F。求证△ACG∽△AFC。

分析：题目已经满足一对公共角相等的条件，即∠CAG=∠FAC。因为已知条件不涉及两三角形的边长，所以考虑借助圆中角的转化，再求证一对角相等，从而证得两三角形相似。

方法1：利用同弧，构造等角。如图7-2，连接BC，得∠B=∠F；由直径AB知∠ACB=90°。∵CD⊥AB，∴∠ADC=90°。由同角的余角相等，得到∠B=∠ACD，因而∠F=∠ACD，证得结论。

设计意图：方法2通过添加辅助线，构造垂径定理基本图形，由垂径定理得到等弧。由等弧得到等角，进行圆中角的转化，有利于学生将陌生图形转变为自己熟悉的图形。

练习7：如图8-1，已知AB=AC=AD，∠CBD=2∠BDC，∠BAC=44°，则∠CAD的度数为（ ）

A.68° B.88° C.90° D.112°

设计意图：有些图形问题虽然从表面上看与圆无关，但若能发现其中共圆的点、隐含的圆，就能运用圆中角的转化解决问题，让问题实现从复杂到简单、从隐性到显性的转变。

结语

文中以圆中角的转化为例，让学生掌握如何应用转化思想解决问题，感受转化的作用，即化抽象为直观、化生疏为熟悉、化复杂为简单、化隐性为显性，进而领会数学思想，提升数学素养。

［参考文献］

王永春.小学数学与數学思想方法［M］.上海：华东师范大学出版社，2014.