冲压空气涡轮气动设计及其规律研究

唐宜文,钟易成

(南京航空航天大学能源与动力学院,江苏 南京 210016)

飞机飞行过程中常会遇到一些复杂的事件导致发动机空中熄火,无法继续为飞机提供电力支持。为了提高飞机飞行的安全性,目前世界上大部分主流民航客机都安装了冲压空气涡轮(RAT)系统[1]。RAT系统在飞机上的应用已有较长的历史,应用效果很好。据统计,从20世纪80年代到21世纪初,全球有十几起飞行事故在RAT系统的帮助下顺利解决,因此深入研究RAT叶片设计对于航空事业的发展有着重要的意义[2]。现代风力机叶片设计大多数都是基于叶素-动量理论,叶素理论是Drzewiwcki在19世纪末提出的,并且W.Froude对叶素理论进行了归纳。Wilson、Walker和Lissaman等人在1974年完成了相关的FORTRAN程序编制工作,对叶素理论做出了细致、系统的阐述和论证。一直以来,风力机的设计者广泛采用这种方法并在这个方法的基础上做出各种改进[3-6]。

对冲压空气涡轮进行传统的气动分析需要花费大量的时间,同时也需要研究人员具备很高的专业素质和丰富的经验。本文采用计算流体力学(CFD)仿真的方法,通过解析N-S方程得到流场各处的数值。相比较传统的气动分析方法而言,CFD仿真方法可以有效地在短时间内得到流场参数,为研究人员提供参考,极大地缩短研发周期,节省研发成本[7-8]。

1 冲压空气涡轮气动外形设计

基于叶素-动量理论的Wilson设计法是目前最常用的方法,在小型叶片设计中应用较多。

1.1 叶素-动量定理

由动量理论可得:

dT=4πρV2a(1-a)rdr

(1)

dM=4πρΩVb(1-a)r3dr

(2)

式中:T为力矩,ρ为密度,V为来流速度,a为轴向诱导因子,r为叶片叶高,M为转矩,Ω为角速度,b为切向诱导因子。

由叶素理论可得:

(3)

(4)

式中:B为叶片数目,Cn为法向力系数,c为弦长,Ct为切向力系数。

由式(1)～式(4)可以得出:

(5)

(6)

其中:

式中:φ为气流倾角,σ为弦长实度。

Wilson设计理论与传统的叶素-动量理论不同,Wilson设计法充分考虑了叶尖漩涡对诱导速度的影响,通过引入叶尖损失修正因子弥补叶素-动量理论的不足。Wilson修正方法的表达式为:

(7)

本文采用Wilson设计法对叶片进行气动设计,并对建模方法进行编程以实现参数化设计。

1.2 冲压空气涡轮设计流程

冲压空气涡轮设计流程如图1所示。先由动量理论计算冲压空气涡轮整体性能,再由叶素理论沿叶高计算各个微元段在最佳气流倾角设计下的安装角和弦长。将各个微元段的性能沿叶高积分,最后得到冲压空气涡轮的整体性能。将调整过弦长和安装角的叶片模型输出,通过软件进行三维建模,再通过CFD进行仿真。

图1 冲压空气涡轮设计流程图

1.3 设计条件及设计结果

本文设置的算例转速为8 000 r/min,叶片数为2,设计叶片截面数为3(分别为ARA-D6%、ARA-D10%、ARA-D13%,根据Profili软件可以得到翼型做功较大的最佳气流倾角分别为5°、6°、9°),微元截面数设置为11。

根据设计参数,得到最佳的冲压空气涡轮参数为:流量21.26 kg/s,叶尖速比3.50,输出功率53.43 kW,推力112.17 kg,风能利用系数0.511,推力系数0.84,轴向诱导因子0.328,切向诱导因子0.051。计算得到冲压空气涡轮不同叶高下对应的弦长与安装角,见表1。

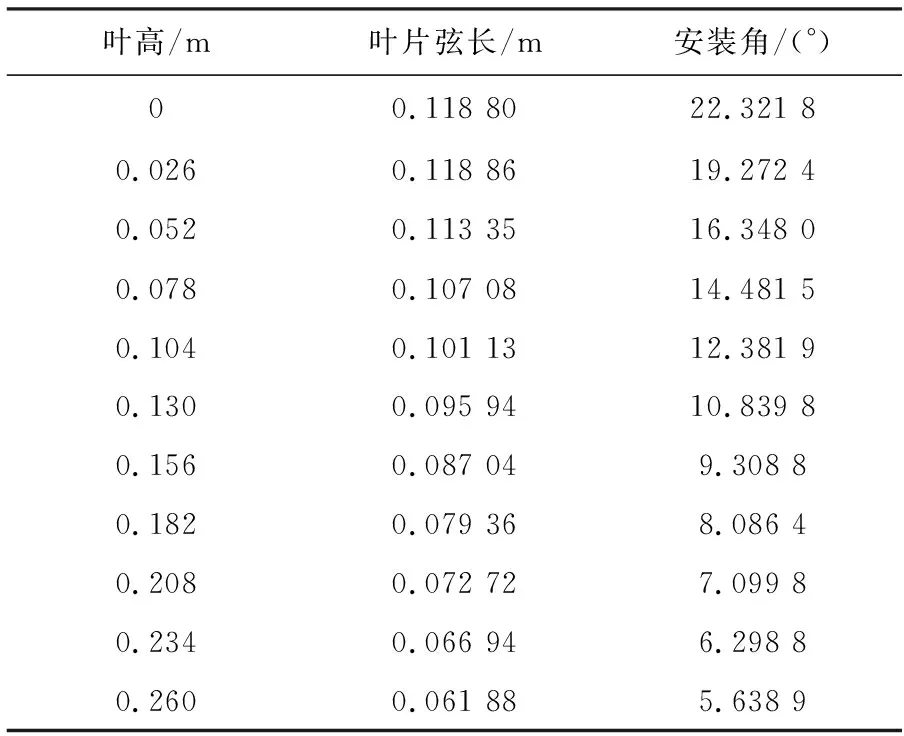
表1 叶片叶高与对应位置翼型弦长

2 模型及网格

将叶片模型与轮毂模型合并得到完整的冲压空气涡轮模型,如图2所示。

图2 冲压空气涡轮模型

三维网格划分采用结构化网格,网格模型分为内、外两个流场单独划分,内流场与外流场之间设置交界面。外流场网格数为60万,内流场网格数为220万,如图3、4所示。

图3 远场网格图

图4 内流场叶片及轮毂处网格图

3 仿真结果及分析

3.1 不同来流速度下的最佳安装角

在定转速下分析不同安装角下不同来流速度时的冲压空气涡轮输出功率。来流速度分别为80、110、140、170、200 m/s,安装角分别为22°、28°、34°、40°、46°、52°,运用CFD-Post计算叶片扭矩,换算成叶片输出功率及功率系数。绘制不同来流速度、相同安装角与输出功率曲线图,不同安装角、相同来流速度与输出功率曲线图。

图5为转速为8 000 r/min条件下的来流速度与冲压空气涡轮输出功率曲线图,由图可以看出,6种安装角下冲压空气涡轮输出功率都随着来流速度的增加而增加。安装角为22°～34°、来流速度在110 m/s以上时,冲压空气涡轮输出功率均大于40 kW;在来流速度大于140 m/s时,只要攻角小于52°,输出功率都超过40 kW。在58°攻角下,功率出现负值,这是因为此时冲压空气涡轮因攻角过大而出现大面积的流动分离,导致驱动叶片做的功不及维持冲压空气涡轮以额定功率旋转所需的功。

图5 不同来流速度、安装角与输出功率曲线图

图6所示为转速为8 000 r/min条件下冲压空气涡轮输出功率随安装角变化的曲线图。由图可以看出,在来流速度一定的情况下,冲压空气涡轮输出功率随着安装角的增加而增加,到达一定值后,再随着安装角的增加而减小,因此存在一个最佳的安装角使得冲压空气涡轮在该来流速度下输出功率最大,气动性能最佳。来流速度较小时,对应的使风轮做功最大的安装角较小;来流速度较大时,对应的使风轮做功最大的安装角较大。通常情况下,飞机上的冲压空气涡轮都带有安装角自动调节装置,可以使叶片安装角随来流速度的变化而变化,以保证冲压空气涡轮输出的功率处于最佳状态。

图6 安装角与输出功率曲线图

3.2 偏航角对冲压空气涡轮性能影响

偏航风向固定,风向与转轴保持在偏航角为γ,假设通过冲压空气涡轮圆盘的质量流量的变化率乘以冲压空气涡轮平面的速度变化率等于轴向上动量的变化率,则可以得到:

F=ρAdU∞(cosγ-a)2aU∞

(8)

式中:F为冲压空气涡轮轴向推力,Ad为冲压空气涡轮圆盘面积,U∞为来流速度。

此时,推力系数CT为:

CT=4a(cosγ-a)

(9)

冲压空气涡轮盘产生的功率为:

FU∞(cosγ-a)

功率系数Cp为:

Cp=4a(cosγ-a)2

(10)

CFD计算值与cos3γ评价法则评价值对比结果见表2。当偏航角为15°时,冲压空气涡轮功率减小了约10%,cos315°计算值为0.901,即功率损失为10%;当偏航角为30°时,冲压空气涡轮的功率减小了33%～40%,cos330°计算值为0.649,即功率损失为35%;当偏航角为45°时,冲压空气涡轮功率减小了60%～75%。这是因为偏航角过大时流动分离严重,扭矩减小,导致功率下降。由以上分析可知,当偏航角小于15°时,可以较好地预测冲压空气涡轮的功率,随着偏航角的增加,这种方法不再适用。

4 结论

本文采用软件编程实现冲压空气涡轮气动设计,通过CFD对冲压空气涡轮性能进行仿真,得到以下结论:

1)采用Wilson设计方法设计出的冲压空气涡轮在性能较高。

2)每一来流速度都对应一个最佳的安装角使冲压空气涡轮的输出功率最大,越高的来流速度对应的最佳安装角越大。

3)随着偏航角增加,冲压空气涡轮的性能下降。在偏航角小于15°时,冲压空气涡轮性能下降规律满足cos3γ评价法则,但是随着偏航角的增大,这个法则不再适用。