平面向量的极化恒等式解题研究

刘胜男

⦿ 哈尔滨师范大学教师教育学院

高考对于向量部分知识点的考查中,数量积运算占比极大,解决平面向量数量积问题主要有公式法和坐标法这两种常规方法.本文中介绍一种新的解法,利用极化恒等式解决一般方法不容易计算的数量积问题,特别在“求取值范围”问题中有着广泛应用.“极化恒等式”这一内容源自大学数学“泛函分析”,它表明数量积可以由它诱导出的范数来表示,把极化恒等式降维至二维平面,则可以非常巧妙地建立起向量数量积与向量模长之间的联系,即仅用向量模长表示向量的数量积,从而实现向量和几何、向量和代数的精妙结合.

1 极化恒等式

极化恒等式标准形式:对于两个非零向量a,b,有

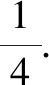
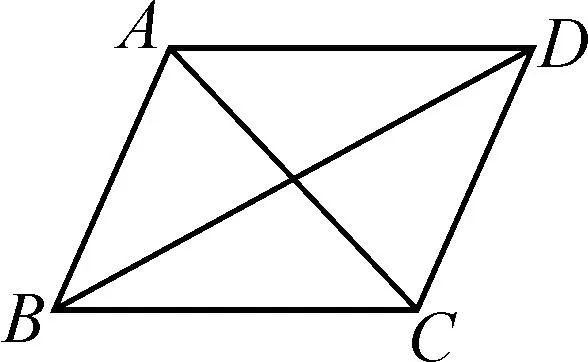
图1

推广1如图1,在ABCD中,有

在平行四边形中,可以用它来解决一些与数量积范围或最值相关的问题,同时保留了更直观的几何意义.当然,也可以在三角形中构造极化恒等式,这也是极化恒等式的第二个推广.

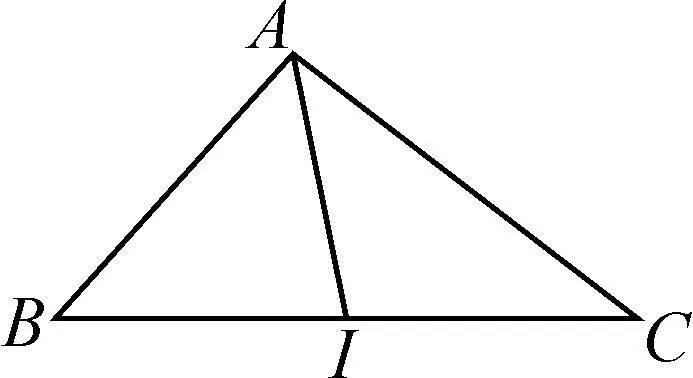
图2

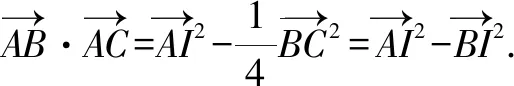
2 极化恒等式的优越性

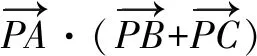
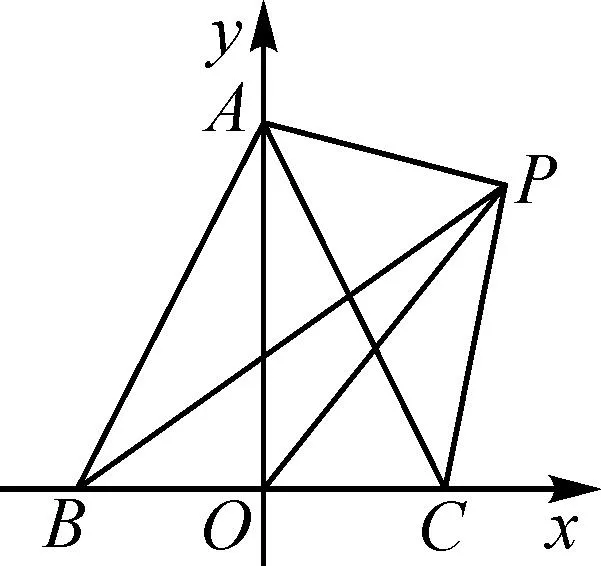
图3

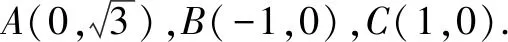
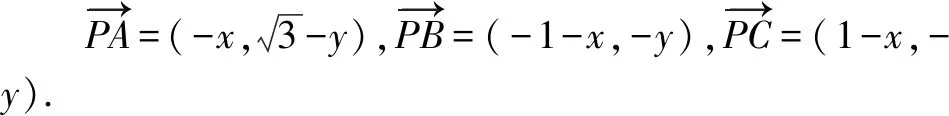
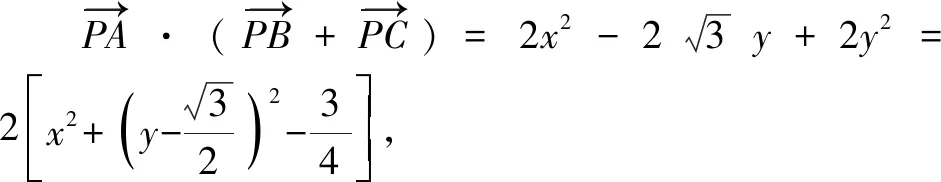
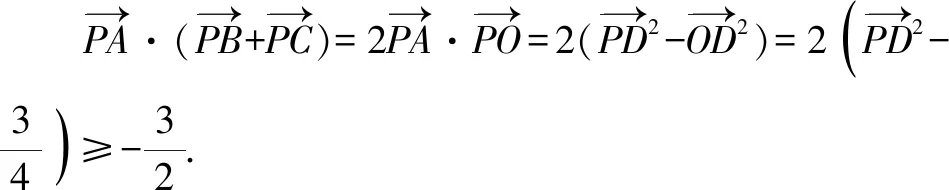
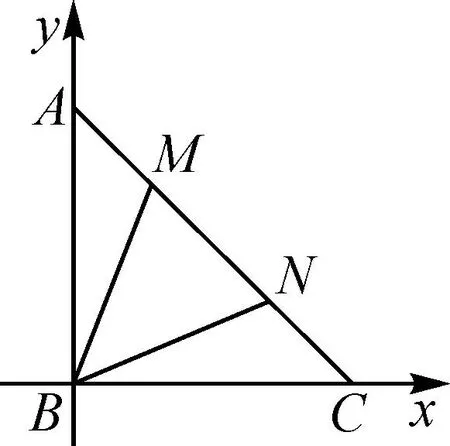
图4

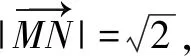
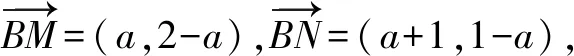
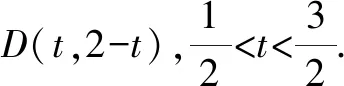
点评：从例1及其变式的解法可以发现,使用常规坐标法步骤繁琐,在计算上花费时间较长,还可能会由于疏忽导致做错,而采用极化恒等式法,只需找到三角形边的中点,可以代入公式,题目便迎刃而解.把平面向量数量积这种抽象的问题转变为代数问题进行求解,可以简化计算.解法2体现出极化恒等式在计算向量的数量积中的优越性.

3 极化恒等式的应用举例

题型1：定值问题.

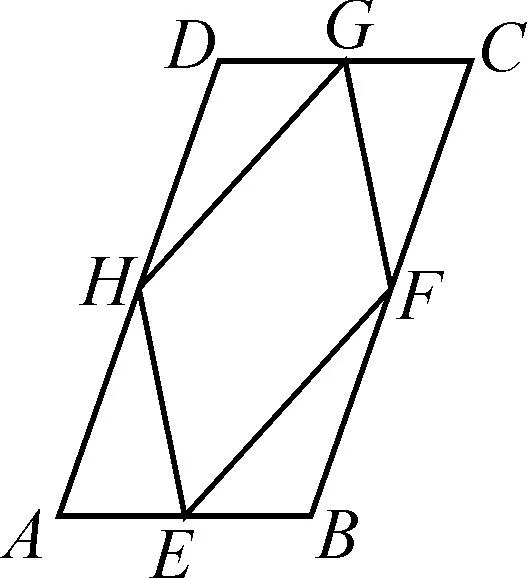
图5

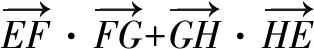
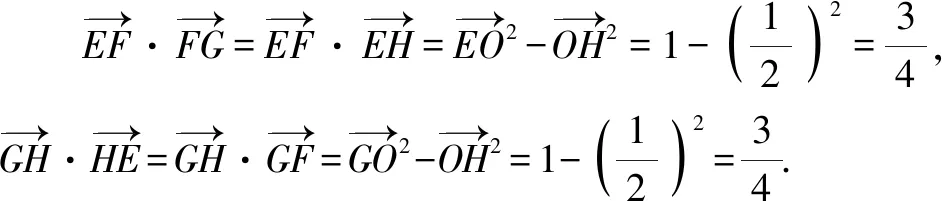
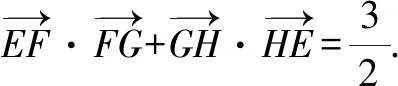
题型2：范围问题.

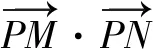
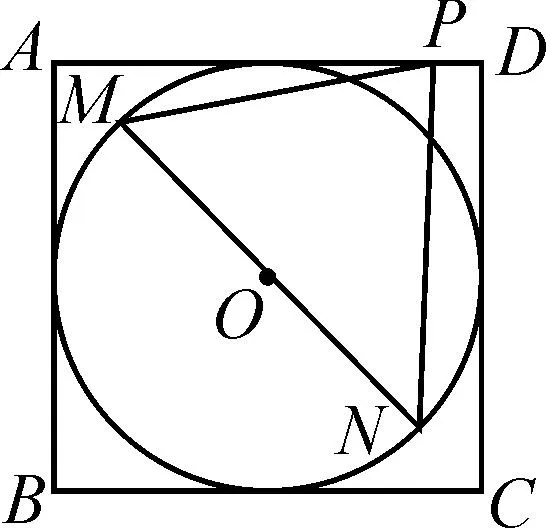
图6

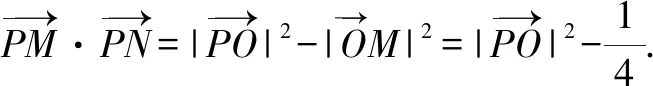
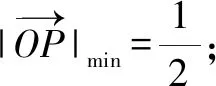
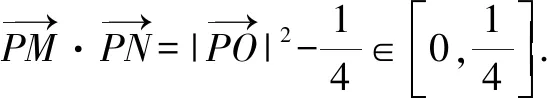
题型3：求参问题.

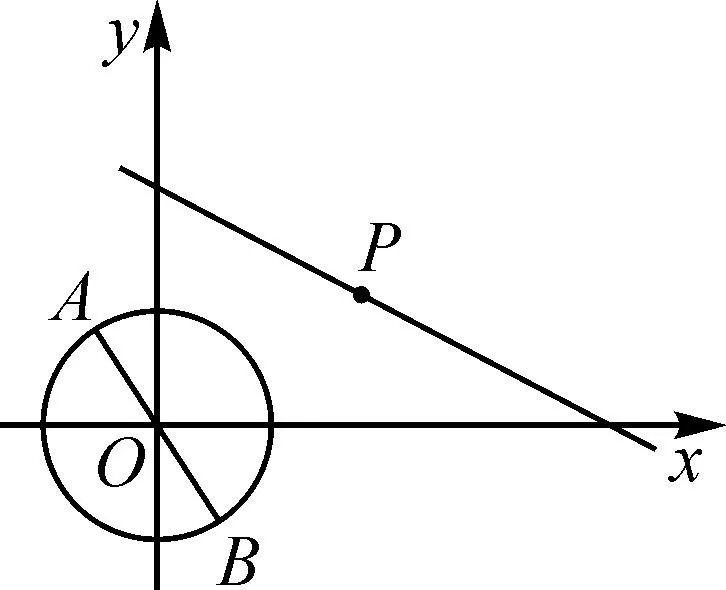
图7

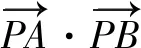
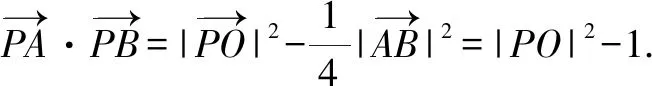
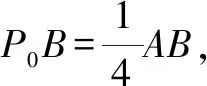
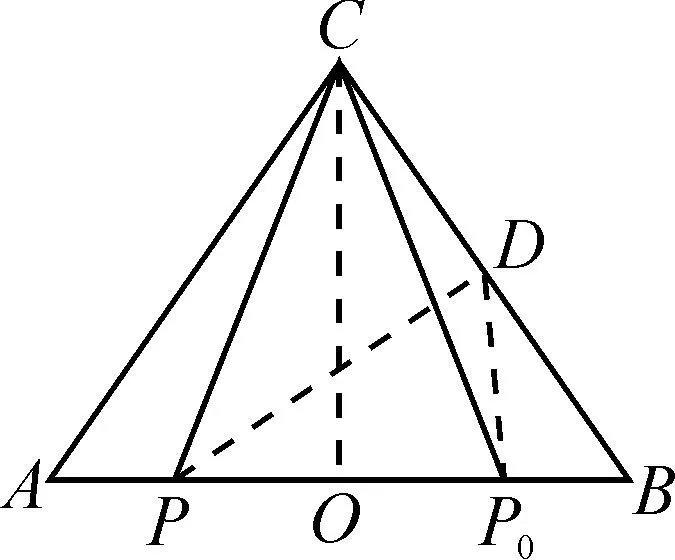
图8

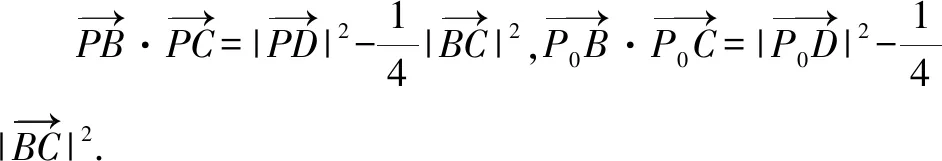
4 总结

数学解题不是简单的做题训练,它更像是知识的再创造.解题是学习数学的重要一环,学会了解题意味着学生不仅具备了解决新问题的能力,同时也培养了他们的逻辑思维、创造性思维和问题解决的技能.利用极化恒等式可以求数量积的值、界定数量积的取值范围、探求数量积的最值、处理长度问题,以及解决一些综合性问题.因此,教师站在更高层面,为学生讲解一类新的解题模型是有必要的[1].