高中数学课堂“问题串”的设计
——以“平面向量基本定理”教学为例
隗雪娜
⦿ 哈尔滨师范大学教师教育学院
“疑是思之始,学之端.”疑问是思考的开始,也是学问的开始.教师想要上好一堂高效生动的数学课就要设置有效的问题,以问题来驱动学生学习,培养学生的探索精神,提高学生分析和解决问题的能力.然而有效的数学课堂并不是用简单的几个问题来填充就可以的,而是需要一系列的问题串,并且问题和问题之间有着逻辑关系等要求,引导学生步步深入,逐步习得知识,学生会有种豁然开朗的成就感.
1 “问题串”设计基本理念
问题串主要是指在一定的主题内围绕特定目标,按一定逻辑关系等设计出一系列问题,这些问题不能少于3个,并且利用这些问题能有效开展教学.每组问题串都有各自的目的,都是为教学目标服务.问题串的设计要打破传统教学中随意将问题抛出的现象,并由此营造出有序高效的学习氛围.问题串教学并不是教师的舞台,而是学生作为主体施展聪明智慧、努力探索的舞台,是教师通过提出一个又一个问题引发学生思考、层层递进习得知识的过程.
问题串有着双重作用.一方面,教师可以对本节课有一个整体的把握.教师设计本节课首先要明白教学目标是什么,然后根据教学目标设计一系列有逻辑、螺旋上升式的问题串,同时对本节课的重点有一个清晰的认知.另一方面,能让学生的思维能力等得到发展.通过教师抛出的一个又一个问题,学生一步一个脚印地完成学习目标,提高思维水平,培养问题意识,提升发现问题、提出问题、分析问题、解决问题的能力.除此之外,问题串教学往往会涉及小组讨论、师生合作等活动,这也会调动学生探索的积极性,培养学生的动手操作能力以及数学表达能力,变被动学习为主动学习,在解决问题的同时既获取了知识又提升了数学素养.
2 “问题串”的设计要求
2.1 “问题串”要围绕教学目标
教学目标既是教学的起点,也是教学的终点.教师在进行教学设计时要精准分析教学目标,并有针对性地设计问题,将教学内容分成一个或多个核心内容,并相应地设计一组或多组彼此紧密联系的问题串.学生在探索、解决问题的过程中,逐一理解知识点,在课堂互动中加深对数学概念、定理等的理解,在头脑中对知识进行系统建构,将新知识纳入到自己的认知结构中,实现从细节到整体的转变,并最终达到教学目标的要求.
2.2 “问题串”要立足于学生认知
首先,根据维果斯基的最近发展区理论,教师在设计问题串时,应当充分了解学生的认知水平.问题串要符合学生的认知水平,设置的问题过易或过难都会使学生失去学习激情;设置的问题要符合学生的最近发展区,让学生蹦一蹦可以够得到,这样会激发学生的学习兴趣和继续探索的热情,并且在解决问题的过程中能感受到探索的快乐和成功的喜悦,进一步培养分析和解决问题的能力.
其次,关注学生的认知水平以及最近发展区,也是将传统的以教师为中心的教学转变为以学生为中心的教学.教师在设计教学和实施教学的过程中要时刻关注学生的学习情况和状态,努力通过问题串驱动学生学习,促进他们进入最佳的思维状态,化被动学习为主动学习.
2.3 “问题串”要具有目的性
教师设计问题串需要经过深思熟虑,在认真研究教材、课标的基础上进行设计.问题串中的每个问题都有其存在的意义,并不是突发奇想随意提出来的.因此,教师要明确每个问题的目的是为了唤起学生的回忆,或是激发学生的学习兴趣,又或是引导学生深入思考等,要在课堂上逐步提出问题,让学生在一个个问题解决的过程中理解并掌握本节课的教学重点和难点.
2.4 “问题串”要具有层次性
问题串起着引导课堂教学的作用,因此问题串的设置要有一定的层次性.问题的设置应由浅入深、由表及里、循序渐进、螺旋式上升,一步步引导学生深入思考.由于学生的水平不尽相同,因此在设置问题时要考虑到学生的个体差异性,问题设置需分层次,小梯度,尽量满足所有学生的学习需求.比如,对于学生来说有一定难度的知识,可以将复杂问题分解,从学生的原有认知水平出发,考虑学生最近发展区,设置几个由浅到深的问题,最终引领学生习得知识.在一个个梯度问题的解决中,激发学生继续探索的兴趣,拓展思维的广度和深度.
2.5 “问题串”要具有逻辑性
教师利用问题串来驱动学生的思维,在设计时要考虑学生的思维逻辑和知识逻辑.问题不是随意提出的,而是教师精心将教学内容的知识点利用问题串联起来,在学生学完本节课回顾所学内容时,能说出本节课知识点的脉络,由此及彼、触类旁通.这不仅能培养学生严密的思维逻辑,还可以使学生养成良好的思维习惯.
2.6 “问题串”要体现启发性
根据启发性教学原则,教师在教学过程中要注意时时刻刻启发学生.教师要把握好问题串的呈现方式,如果简单直白地提出问题,而不考虑学生,那将毫无意义.通过一个个问题,将学生引入问题情境,并在问题情境中沉浸,主动解决一个个问题,在问题探究中认知、理解、掌握数学知识,并有效汲取和内化知识,进而启发学生独立思考、判断的能力,提高教学效果.
3 “问题串”教学案例分析
3.1 创设情境
经过前面的学习,我们知道平面内的向量是无穷多的.那么,能否仅用几个“基础”向量而将所有的平面向量表示出来呢?最少需要几个“基础”向量才能表示所有的平面向量呢?
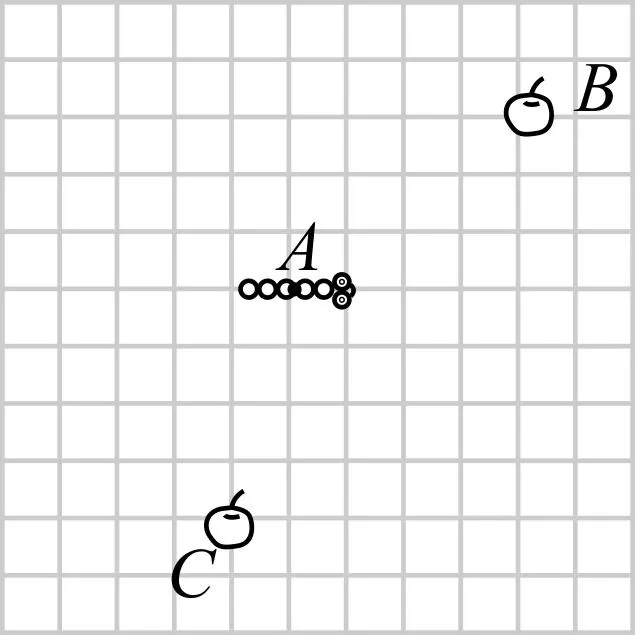
图1
问题1贪吃蛇通过在屏幕上下左右四个方向移动就可以吃到屏幕上任意一点处的食物.如图1,贪吃蛇在A处想要吃到B处和C处的苹果,那它可以怎样行动?行动路径唯一吗?试各举出其中一种行动路径.
3.2 探究“基础”向量

图2
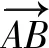
问题3想要表示平面内的任意向量,需要几个“基础”向量?
问题4这4个向量就是我们所需要数量最少的“基础向量”吗?这四个向量是否有内在联系,可以帮助我们减少“基础”向量的个数吗?
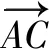
追问:两个“基础”向量一定垂直吗?
设计意图:引入向量,让学生发现数学知识与我们的生活息息相关,激发学生的学习热情.利用问题串的形式,引导学生发现“基础”向量的个数,一步步探究,为后面学生理解平面向量基本定理作辅垫,培养严密的思维习惯,拓展思维的广度和深度.
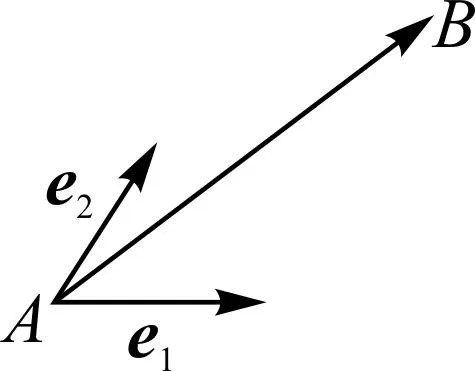
图3
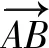
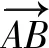
问题7是不是所有的平面向量均可以用e1,e2来表示?
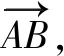
设计意图:遵循知识的逻辑和学生原有的认知水平,一个个问题让学生直观感受平面内任意一个向量都可以用两个不共线向量表示出来,加深对定理的探究,学生的思维能够一直保持活跃,教师更能够有效教学.
问题8经过前面的探索,我们发现两个向量e1,e2就可以将平面内任意一个向量表示出来.那么,任意两个向量均满足要求吗?如果两向量共线还可以吗?
预设学生回答:如果两个向量共线,只能表示与这两向量共线的向量,而不能表示平面内所有的向量.
问题9这样,我们所研究的“基础”向量就减少到两个不共线的向量.请问,可以用一个非零向量来表示平面内的所有向量吗?
预设学生回答:1个非零向量只能表示与之平行的向量,而不能表示平面内所有的向量.
综上,我们发现最“基础”的向量就是两个不共线向量,用这两个不共线的向量可以将平面内的任意向量a表示为a=λ1e1+λ2e2.其中称e1,e2为基底.
设计意图:教师在教学中充分调动学生的积极性,培养学生的归纳能力和数学表达能力.学生通过问题的逐个击破,对所得到的结论印象更加深刻.
3.3 探究定理
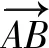
预设学生回答:基底不一样,基底有无数对.
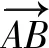
问题11当给定a和一组基底e1,e2,a=λ1e1+λ2e2这种表示唯一吗?
师生活动:师生共同利用“反证法”证明λ1,λ2的唯一性.
这是从代数的角度证明λ1,λ2的唯一性,那么能否从形的角度进行证明呢?大家课后进行思考并操作.
设计意图:引导学生动手操作判断基底的不唯一性以及验证λ1,λ2的唯一性,让学生直观感受到数学的严谨性和魅力,培养从多方面分析、解决问题的能力和动手操作能力.
学生试着总结平面向量基本定理:
如果e1,e2是同一平面内的两个不共线向量,那么对于这一平面内的任一向量a,有且只有一对实数λ1,λ2,使a=λ1e1+λ2e2.
设计意图:层层深入引导学生探索,从简单到复杂,从特殊到一般,让学生亲身经历定理的发生、形成过程,并体会探索问题的思路.
3.4 总结提升
大家回忆一下本节课学到了什么呢?
(1)平面向量基本定理的内容;
(2)平面向量基本定理可以联系物理学中力的分解模型来理解,它说明在同一平面内任一向量都可以表示为不共线的两个向量的线性组合,其本质是一个向量在其他两个向量方向上的分解.
4 教学启示
教师是用教材教,而不是教教材.教师在认真备课后,不必就课论课,可以将本节课内容与前面所学习的知识建立联系,像“串糖葫芦”一样设置问题串,一个接一个地引导学生进入学习状态,调动学生的积极性与学习热情.问题串的目的性可以引导学生去发现、分析、解决问题,养成问题意识,建立数学思维,能够深入问题内部,进而在主观能动性的驱使下“可持续”地解决问题.
将问题串应用到实际课堂中,要注意灵活性.因为学生的思维很活跃,所以在教学过程中应根据探求需要及时调整问题串,使得学生的思维连贯,“上台阶”似地一步步达成学习目标.教师要注意给学生留思考时间,不要被问题串困住,而是运用问题串带动学生积极思考,让学生主动进行探究,获得更多的成功体验.教师在进行问题串教学时,不能每节课都套用一个模板,要及时反思,不断精进问题串的设置,根据课型选择适合的问题串,不断提高问题串的质量.Z

