基于离散面阵的超大规模MIMO近场性能分析

易文慧,王 者,肖华华,章嘉懿

(1.北京交通大学 电子信息工程学院,北京 100044;2.中兴通讯股份有限公司,广东 深圳 518057)

0 引言

下一代移动通信网络在低接入延迟、高传输数据速率和低误码率等方面的需求越来越高。作为潜在的新一代通信技术之一,超大规模多输入多输出(Extremely Large-scale Multiple Input Multiple Output,XL-MIMO)技术凭借其提供的高频谱效率、高能量效率和海量接入能力而受到工业界和学术界的广泛关注。XL-MIMO技术与传统的大规模多输入多输出(massive Multiple-Input Multiple-Output,mMIMO)技术相比,在信号传输过程中带来了新的近场球面波传播特性,亟需采用改进的近场信号处理算法,从而提高频谱效率和空间自由度[1]。

从mMIMO到XL-MIMO不仅意味着天线数量的增加,还意味着电磁场结构的根本变化。电磁波的辐射场可以分为远场区域和近场区域。文献[2]对XL-MIMO远场信道和近场信道进行了比较,揭示了二者的差异性。由于毫米波(millimeter Wave,mmWave)和太赫兹(Terahertz,THz)提供的丰富高频带宽,信号的穿透损耗较低频时更加严重,所以覆盖范围缩小,且信号传输的衍射效应可以忽略,因此自由空间中XL-MIMO的近场传输以视距(Line of Sight,LoS)传输为主[3]。

信道容量是研究XL-MIMO性能的一项重要性能指标。文献[4]提出了注水算法对每个数据流进行最优功率分配,进而推导出了XL-MIMO系统的信道容量与天线阵列中天线数之间的关系。但是,对于近场的LoS XL-MIMO系统,由于其信道矩阵的稀疏性,无法进一步简化为精确的解析解。

为了计算出XL-MIMO信道容量的解析表达式,文献[5]提出可以利用有效自由度(Effective Degrees of Freedom,EDoF)的概念来描述系统信道容量。文献[6]在此基础上提出了一种新的方法,推导出了基于均匀线性阵列(Uniform Linear Array,ULA)的系统信道容量解析表达式。文献[7]对基于均匀环形阵列(Uniform Circular Array,UCA)和ULA的系统EDoF和信道容量进行了比较分析。

在现有研究中,XL-MIMO系统的EDoF和信道容量解析表达式的推导大多考虑基于ULA的系统,没有对基于均匀平面阵列(Uniform Planar Array,UPA)的系统进行拓展。但是事实上近些年来UPA的XL-MIMO也被认为是一个有前途的方案,这类系统大多是在发射端和接收端配备一个矩形或者正方形的平面,天线元件沿着平面的水平和垂直方向密集排列[8]。因此,为了更好地研究基于UPA的XL-MIMO系统的物理实现和对其进行性能分析,本文针对基于UPA的下行近场XL-MIMO系统,首先推导了EDoF的解析表达式,该表达式描述了等效单输入单输出(Single-Input Single-Output,SISO)通道的数量;然后利用推导出的EDoF得到信道容量的解析表达式;最后通过仿真结果对XL-MIMO系统性能进行了评估。数值结果证明了解析表达式的正确性。同时,仿真结果证明随着通信距离的增加,EDoF和信道容量降低,并且随着面阵天线数量的增加和天线间距的减小,离散面阵下的EDoF会趋近于定值。

1 信道模型

如图1所示,在下行XL-MIMO系统中,发射机和接收机都装配了UPA,发射机的其中一个顶点位于三维平面R3的原点,发射机的天线阵列与接收机的天线阵列均垂直于xoy平面且互相平行[9-10]。

图1 信道模型示意图Fig.1 Schematic of the channel model

发射机天线阵列尺寸为Lt×Lv,Lt表示发射阵列水平宽度,Lv表示发射阵列垂直高度,发射机天线数量为M=Nt×Nv,每一行有数量为Nt的天线,每一列有数量为Nv的天线。接收机天线阵列尺寸为Lr×Lh,Lr表示接收阵列水平宽度,Lh表示接收阵列垂直高度,接收机天线数量为N=Nr×Nh,每一行有数量为Nr的天线,每一列有数量为Nh的天线[11]。假设天线之间的间隔均相等,q表示天线之间的间隔,le表示每个天线的孔径长度,其中le∈(0,q]。

对于发射面,M个天线被均匀部署在面积为Lt×Lv的平面上,这些天线按m∈[1,M]逐行进行索引,因此图1中发射机第m个天线的位置rtm∈R3表示为[12-13]：

rtm=[0,i(m)q,j(m)q]T,

(1)

式中:i(m)=mod(m-1,Nt),j(m)=(m-1)/Nt」分别表示第m个天线在发射面上的水平索引和垂直索引。需要注意的是,[.]T表示向量的转置,mod(.,.)表示模量操作,.」表示向下取整操作。

同理,可得到接收机第n个天线的位置rrn∈R3表示:

rrn=[xr,yr+t(n)q,zr+k(n)q]T,

(2)

式中:t(n)=mod(n-1,Nr),k(n)=(n-1)/Nr」。

发射机与接收机之间的信道矩阵H∈CN×M表示为[14]：

(3)

式中:Gn,m为发射机的第m个天线与接收机的第n个天线在单位区域内的信道增益。用λ表示信号波长,在自由空间内,Gn,m可以表示为[15-16]：

(4)

(5)

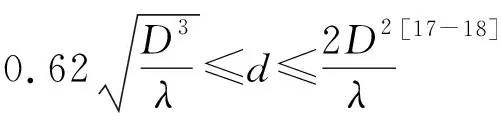
信道相关矩阵R∈CM×M可以表示为[19]：

R=HHH,

(6)

式中:(·)H表示矩阵的共轭转置操作。

文献[4]中基于注水算法得到系统信道容量的表达式:

(7)

在近场中,由于球形波的影响,H的奇异值相互变化,可以利用EDoF的概念来表示系统的容量:

(8)

式中:‖H‖F=tr(R)表示总信道功率,tr(.)表示求矩阵的迹,‖.‖F表示求矩阵的F-范数,ε为EDoF可以表示如下[20]。

(9)

2 有效自由度和信道容量分析

为了计算EDoF的解析表达式,首先需要对信道相关矩阵R进行表示,将式(4)代入式(7)中,可以得到:

(10)

因此可以得到:

(11)

(12)

将式(11)和式(12)代入式(9),EDoF的表达式可以表示为:

(13)

从式(10)中可以得到:

(14)

式中:

(15)

(16)

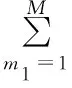
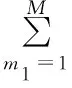
(17)

将式(2)和式(3)代入式(17),因在辐射近场中,发射机和接收机间的距离远大于天线阵列尺寸,可得:

(18)

将式(2)、式(3)和式(16)代入式(11),可得到:

(19)

将式(18)和式(19)代入式(13),可得近场LoS环境下基于UPA的XL-MIMO系统EDoF的解析表达式:

(20)

式中:q=Lr/Nr。

经过EDoF解析表达式的计算,可以得到基于UPA的XL-MIMO在近场环境下信道容量的解析表达式;

(21)

将式(11)和式(20)代入式(21),可以得到:

(22)

式中:

3 仿真分析

本节通过仿真结果来验证前文中的分析结果,并且说明基于UPA的XL-MIMO的近场特性。考虑频率f=28 GHz,N0=-60 dBm,le=(1/16)λ,yr=0,P=10 dBm,发射面与接收面的天线数量和面阵尺寸均相等。涉及的仿真参数如表1所示。

表1 仿真参数Tab.1 Simulation parameters

图2为发射面与接收面中心相对高度h=|zr|不同的情况下EDoF随天线数量的变化曲线,验证了近场中基于UPA的XL-MIMO系统EDoF解析表达式的准确性。设置发射面和接收面均为边长为80λ的正方形平面,两平面的水平距离为10 m,保证发射天线与接收天线之间的距离在辐射近场的范围内。图中的折线表示不同相对高度下式(9)的仿真曲线,黑色圆点表示EDoF解析表达式的仿真结果。通过图2可以发现,随着天线数的增加,基于UPA的XL-MIMO系统的EDoF不断增加,最终会发生收敛,且高度h越大时,收敛的EDoF数值更小。

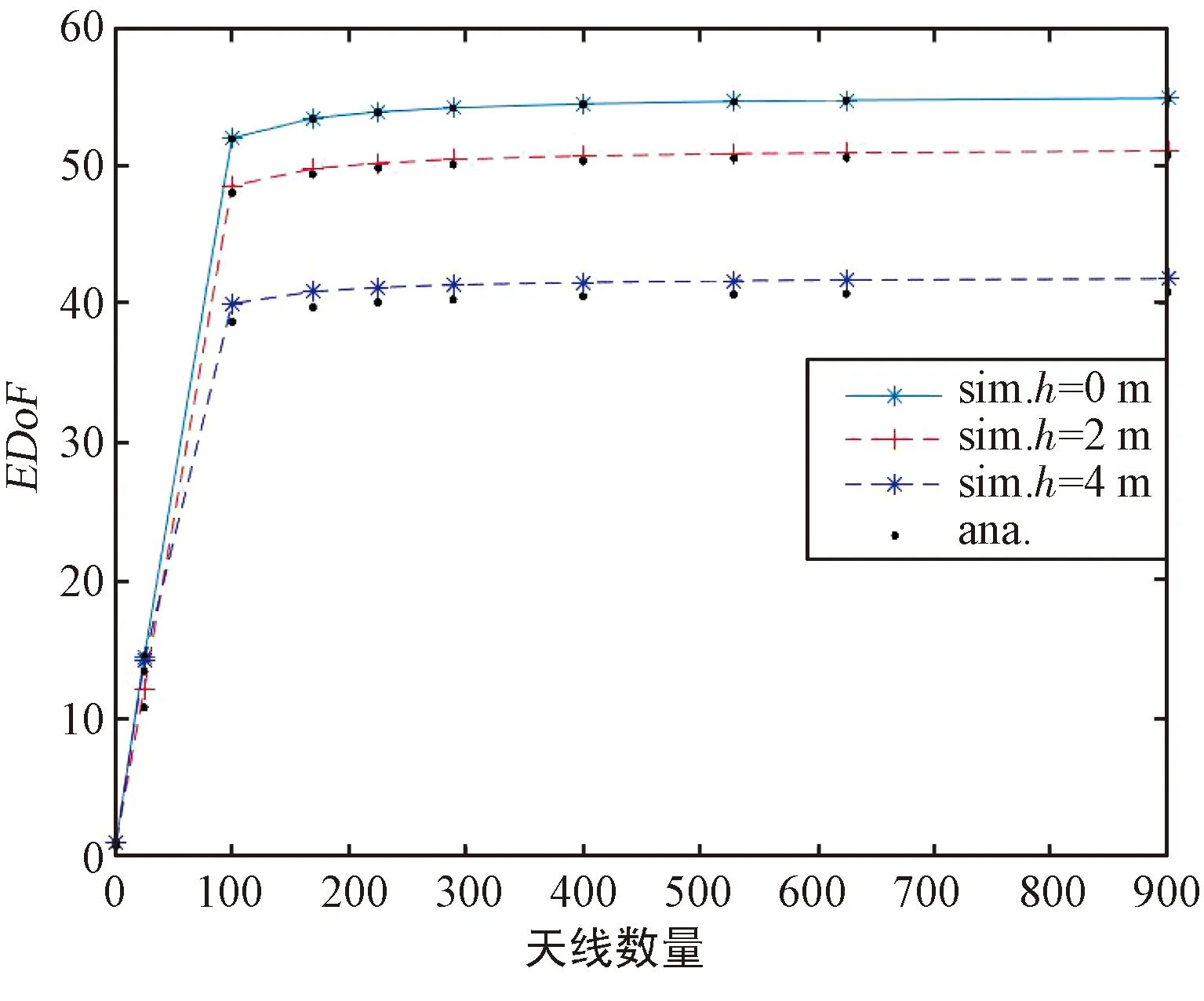
图2 收发面相对高度不同情况下EDoF随天线数量的变化曲线Fig.2 Variation curve of EDoF with the number of antennas for different relative heights of transmitting and receiving surfaces

图3为发射面与接收面水平距离d=|xr|不同的情况下EDoF随天线数量的变化曲线,同样验证了近场中基于UPA的XL-MIMO系统EDoF解析表达式的准确性。设置发射面和接收面均为边长为80λ的正方形平面,两平面中心在同一水平面上,保证发射天线与接收天线之间的距离在辐射近场的范围内。图中的折线表示不同水平距离d下式(9)的仿真曲线,黑色圆点表示EDoF解析表达式的仿真结果。由图3可以看出,随着天线数的增加,基于UPA的XL-MIMO系统的EDoF不断增加,最终会发生收敛,且水平距离d越大时,收敛的EDoF数值更小。

图3 收发面水平距离不同的情况下EDoF随天线数量的变化曲线Fig.3 Variation curve of EDoF with the number of antennas for different horizontal distances between the transmitting and receiving surfaces

图4为发射面与接收面天线面阵尺寸不同的情况下EDoF随天线数量的变化曲线,验证了近场中基于UPA的XL-MIMO系统EDoF解析表达式的准确性。设置发射面和接收面中心在同一水平面上,且收发面之间的水平距离为15 m。图中的折线表示不同面阵尺寸下式(9)的仿真曲线,黑色圆点表示EDoF解析表达式的仿真结果。由图4可知,随着天线数的增加,基于UPA的XL-MIMO系统的EDoF不断增加,最终会发生收敛,通过比较三种面阵尺寸下的EDoF变化情况,可以发现天线阵列尺寸越大,EDoF的收敛速度越慢,且收敛的数值越大。

图4 收发面中天线面阵尺寸不同的情况下EDoF随天线数量的变化曲线Fig.4 Variation curves of EDoF with the number of antennas for different antenna array sizes in the transceiver plane

图5为信道容量随水平距离d=|xr|的变化曲线,验证了近场中基于UPA的XL-MIMO系统信道容量解析表达式的准确性。设置发射面和接收面中心在同一水平面上,且收发面之间的距离始终在辐射近场内,天线阵列尺寸为65λ×65λ,收发面上均匀设置数量为169的天线。图中的蓝色折线表示式(7)的仿真结果,红色折线表示式(22)的仿真结果,黑色圆点表示由EDoF表示的信道容量解析表达式的仿真结果。通过图5可以发现,随着收发面间水平距离的增加,基于UPA的XL-MIMO系统的信道容量不断减少,且信道容量减少的速度不断放缓,另外,仿真曲线很好地验证了文献[5]中的结论,即虽然基于EDoF的信道容量在某些距离上不能准确地拟合式(7),但是基于EDoF的信道容量表达式更易于处理,且在一定误差范围内能够用来描述信道容量。

图5 信道容量随水平距离的变化曲线Fig.5 Variation curve of channel capacity with horizontal distance

4 结束语

针对基于UPA的近场XL-MIMO系统,本文提出了一种易于分析处理的EDoF计算方法。首先完成了适用于辐射近场的EDoF和信道容量解析表达式的推导,并对解析表达式的求解过程进行了详细的描述。然后完成了对基于UPA的XL-MIMO系统中EDoF和信道容量的仿真,以及对所求解析表达式的仿真。仿真结果验证了解析表达式求解的准确性,针对通信距离和天线阵列大小等关键因素对XL-MIMO近场通信性能的影响机理进行了分析。