氢基竖炉反应器还原域数值模拟研究*
曹玲玲,王宇飞,龙 俊,吉 林,韩骁阳,侯晓川
(1 浙江新时代中能科技股份有限公司,浙江 绍兴 312369;2 江苏大学材料科学与工程学院,江苏 镇江 212013)
中国的钢铁产业是继煤电产业之后我国的第二大CO2排放源,在当今发展低碳经济的迫切形势下,为实现我国“30·60”、“双碳”目标,亟需开发绿色冶金新技术,实现钢铁产业减碳转型[1]。目前,国内外冶金领域均提出了涵盖氢冶金的战略规划,包括欧洲的ULCOS、瑞典的HYBRT、日本的COURSE50项目以及我国的中晋矿业等,以氢代碳的已经逐渐发展成为钢铁企业实现绿色低碳可持续发展的有效途径之一[2]。其中,氢基竖炉已成为目前涉及氢冶金工艺的研发的热点与焦点,广受国内外学者关注[3-5]。
典型气基竖炉反应器内以“对流移动床”的方式工作,但炉内物理能与化学能利用的极度不匹配。针对上述问题,对竖炉反应器还原区域传输特性展开了相关研究,旨在通过上述研究,为氢基竖炉反应器的设计和操作优化提供参考。
1 理论基础与模型建立
1.1 竖炉反应器内反应基础
铁在自然界中多以铁氧化物的形式存在,为了得到可供使用的铁,气基竖炉直接还原铁由气体还原剂还原固态铁矿石。铁氧化物的还原是逐级反应进行的,CO和H2分别作为还原气时的还原过程如下:
(1)CO还原铁氧化物
T>843 K时:
第一阶段 Fe2O3到Fe3O4的反应
3Fe2O3+CO=2Fe3O4+CO2
(1)
第二阶段Fe3O4到FeO的反应
Fe3O4+CO=3FeO+CO2
(2)
第三阶段FeO到Fe的反应
FeO+CO=Fe+CO2
(3)
(2)H2还原铁氧化物
T>843 K时:
第一阶段 Fe2O3到Fe3O4的反应
3Fe2O3+H2=2Fe3O4+H2O
(4)
第二阶段Fe3O4到FeO的反应
Fe3O4+H2=3FeO+H2O
(5)
第三阶段FeO到Fe的反应
FeO+H2=Fe+H2O
(6)
1.2 模型建立
在理论分析的基础之上,本文采用ANSYS商务软件对气基竖炉还原段进行模拟,其模型示意图如图1所示,为简化计算过程,采取二维轴对称模型对气基竖炉还原段进行模拟研究,并进行如下假设:
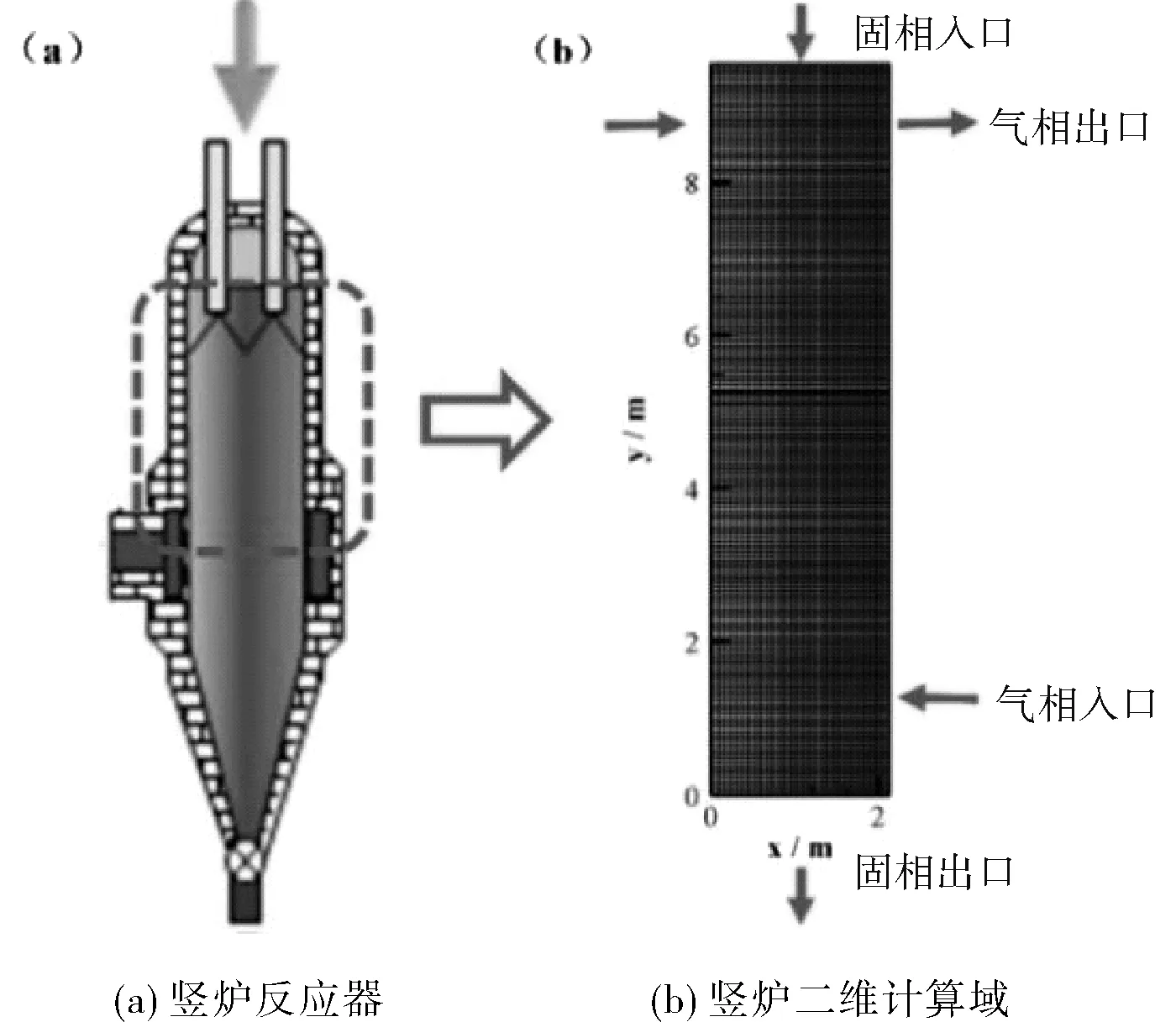
图1 气基竖炉模型图
(1)还原段内物料简化为多孔介质;
(2)铁矿石球团简化为Fe2O3,铁矿石在竖炉内成活塞流匀速下降;
(3)忽略竖炉内温度对还原气体与物料参数的影响;
(4)忽略壁面效应对还原气的影响;
(5)忽略固体炉料间传热,仅考虑气相与固相间的传热;
(6)模拟过程仅考虑物料与还原气的直接化学反应。
1.2.1 基本控制方程
在上述假设基础之上,模拟计算过程遵循的基本方程包括:连续性方程、质量守恒方程、能量守恒方程、动量方程、组分传输方程以及化学反应[6]。对于化学反应的热效应,模拟计算过程中,化学反应热以源项的形式加入能量方程中,化学反应速率常数由Arrhenius公式确定,确定不同阶段表观频率因子和表观活化能。
1.2.2 边界条件
(1)固体计算区域条件:铁矿石球团的初始温度为300 K,还原段的物料设置为多孔介质[7],孔隙率为0.3,黏性阻力系数为1.52×108 m-2,惯性阻力系数为16 963 m-1;
(2)入口边界条件:气体入口边界采用速度入口,速度为5.5 m/s;
(3)出口边界条件:气体出口边界条件设压力出口;
(4)对称边界条件:计算域采用二维轴对称模型;
(5)壁面边界条件:无滑移速度边界条件;竖炉的壁面与还原气的对流换热边界条件为;忽略壁面热量损失。
1.2.3 基本参数
本文选取Gilmore厂的Midrex竖炉反应器(美国俄勒冈州波特兰市)为模拟研究对象[8],涉及基本参数如表1所示。

表1 模型几何参数
1.2.4 数值求解
竖炉几何模型在ANSYS ICEM中建立,将计算域划分为边长2 cm的正方形网格,网格数量为51 516。数值求解过程在ANSYS Fluent中进行,采用瞬态求解器求解,动量方程与能量方程的离散方式采用二阶差分格式,流动模型采用k-ε湍流模型,组分传输方程中设定化学反应,残差精度控制在10-3范围内。在上述模型建立的基础之上,模型的准确性通过实际生产数据进行了验证[8]。
2 结果与讨论
2.1 还原需气量分析
本文以还原1 t直接还原铁(DRI)为例子,分别对还原剂为纯CO、CO∶H2=1∶1、CO∶H2=1∶1.5以及纯H2条件的化学平衡需气量进行计算,在1 093 K时不同还原剂条件下还原气热平衡需气体量依次为:1 666.16 Nm3/t DRI、1 668.42 Nm3/t DRI、1 669.45 Nm3/t DRI以及1 670.47 Nm3/t DRI,化学平衡需气量依次为:1 269.56 Nm3/t DRI、1 205.43 Nm3/t DRI、 1 193.41 Nm3/t DRI以及1 139.99 Nm3/t DRI。
由计算结果可知,在气基竖炉直接还原中,不同还原剂条件下,热平衡与化学平衡需气量均为V化 在氢气竖炉中,当氢气从竖炉的入口进入后,会由于竖炉内部的构造和气体流动的规律,沿径向向上流动。这个过程中,氢气具有初始的动能,但是由于与固体物料之间的摩擦力等因素,其动能会逐渐转化为轴向速度,并逐渐向竖炉炉顶出口转向。在上述过程中,气体在竖直方向上的流速比在水平方向上的流速快得多,因此在竖炉上升的过程中会产生弯曲,最终形成L型流线的形态,如图2所示。 图2 氢气竖炉内气相流线图 同时,气相速度随着径向距离变化速率分布如图3所示,随着径向距离的增加,由竖炉侧壁方向向竖炉中心移动,气相速度沿内径向逐渐衰减,在距离竖炉中心约1.25 m处趋于稳定状态,因此,可推断在氢气竖炉中心附近存在一定的气流迟滞域。 图3 气相速度随着径向距离变化 温度对氢气竖炉反应器内传输行为有重要影响,尤其对于还原反应动力学而言,其限制性环节与温度分布紧密相关。因此,在上述运动规律基础之上,本文对竖炉还原区内温度分布进行了模拟研究。图4显示了竖炉还原域在0.5 h后的温度分布情况。初始阶段,竖炉还原域内的铁矿石球团为常温状态。如图4所示,高温还原气体进入竖炉还原域后,最高温度出现在底部,而顶部的温度最低。在竖炉还原域中心位置,温度梯度高于炉壁,即中心位置的温度变化更大。 图5显示了氢气竖炉高度方向温度随时间的变化过程,由图5可知,在气固传热和还原反应共同作用下,4 h时还原段温度分布达到稳态,稳态时边缘和心部的温度略有差别,还原段高0~8 m内炉料温度趋于1 073 K,与还原气进口温度趋于一致仅在离顶部炉料进口0~2 m内存在较大温度梯度,这是由于还原区上部不断加入的低温炉料所引起的。 本文通过对气基竖炉反应器还原域复杂行为其进行了探究,主要结论如下: (1)还原剂为纯CO、CO∶H2=1∶1、CO∶H2=1∶1.5以及纯H2条件下热平衡需气量依次为:1 666.16 Nm3/t DRI、 1 668.42 Nm3/t DRI、1 669.45 Nm3/t DRI以及1 670.47 Nm3/t DRI,化学平衡需气量依次为:1 269.56 Nm3/t DRI、1 205.43 Nm3/t DRI、1 193.41 Nm3/t DRI以及1 139.99 Nm3/t DRI,热平衡是气基竖炉内实际需气量的限制环节,打破还原气物理热的限制,降低气体需求量,是实现富氢气基竖炉能量高效利用的关键。 (2)氢气竖炉内还原气由入口进入竖炉内,沿径向流动的同时会将初始动能迅速转化为轴向速度,从而逐渐转向竖炉炉顶出口,形成L型流线。气相速度沿内径向逐渐衰减,在距离竖炉中心位置约1.25 m处趋于稳定状态,在氢气竖炉中心附近存在一定的气流迟滞域。 (3)高温还原气体进入竖炉还原域后,最高温度出现在底部,且还原域中心位置存在较大的温度梯度,在气固传热和还原反应共同作用下,还原段高0~8 m内炉料温度趋于稳定。2.2 反应器内还原气运动规律


2.3 还原域内温度分布
3 结 论

