考虑缩尺效应对堆石料颗粒破碎影响的压缩试验研究

卿 云,马爱娟,2,杨少博,2,邱珍锋,2,邓文杰

(1.重庆交通大学 国家内河航道整治工程技术研究中心,重庆 400074; 2.重庆交通大学 水工建筑物健康诊断技术重庆市高校工程研究中心,重庆 400074; 3.重庆川东南工程勘察设计院有限公司,重庆 400038)

0 引 言

堆石料因其具有抗剪强度高、造价低廉、沉陷变形小等特点,多用于土石坝、道路、港口等填方工程中。在坝体高应力条件下,材料容易发生颗粒破碎,使内部的填充关系和局部强度发生改变,造成沉降变形。堆石料的压缩性和颗粒破碎特性的研究通常是借助室内试验完成,受限于室内试验机容许的试样直径,需要对现场填料进行缩尺后才能用于室内试验研究,而试样直径、缩尺方法等发生变化都会对试验结果产生影响。

缩尺方法的改变是通过调整土样中粗、细颗粒的充填关系来影响试样整体的强度和变形特性。傅华等[1]对不同缩尺方法的试样开展了室内三轴试验,发现等量替代法缩尺的级配不均匀系数最大、渗透系数最大,相似级配法缩尺的试样破坏峰值最大、渗透系数最小,混合法缩尺的试样抗剪强度最大、渗透系数介于其它2种方法之间。王思睿等[2]对一组花岗岩材料经4种缩尺方法处理后的试样进行了相对密度试验,研究发现,缩尺方法对试样密度影响显著,4种方法缩尺后替代料密度由大到小分别为:相似级配法、剔除法、混合法、等量替代法。左永振等[3]研究发现试样最大干密度与替代料最大粒径之间呈一种非线性关系,最大粒径由20 mm增至40 mm时,试样最大干密度变化幅度大于最大粒径由40 mm增至60 mm时最大干密度的变化幅度。朱俊高等[4]用混合法得到级配最大粒径为60 mm和20 mm的2组试样,开展了三轴剪切试验,研究发现试样最大粒径与弹性模量和内摩擦角呈正相关,与峰值偏应力呈负相关。

对于同一种试验土料,由试验尺寸之间的差异导致测得的强度指标、变形特性的不同称之为尺寸效应。马刚等[5]用3种不同尺寸(300、400、500 mm)的数值试样,模拟堆石料室内试验三轴加载的过程,同一围压下的3组试样的应力-应变曲线有明显偏移,初始切线模量与试样直径呈正相关,峰值强度与试样直径呈负相关。孔宪京等[6]利用不同型号的设备构建了一个用于研究堆石料尺寸效应的试验平台,试样直径跨度从100 ～1 000 mm,总结大量试样研究成果发现,同种堆石料的尺寸效应在不同围压下表现出的规律不完全相同。

目前对堆石料的缩尺效应研究成果对于开展缩尺效应对颗粒破碎特性的影响研究具有较好的借鉴意义,但是不同学者就尺寸效应对堆石料力学特性的影响规律尚未达成一致的看法,有必要进行深入的探讨。本文从缩尺方法、试样最大粒径及试样直径等方面开展研究缩尺效应对压缩参数、颗粒破碎的影响。

1 试验材料和试验方法

试验所用堆石料为重庆市巫山县庙堂水库主堆石区微风化灰岩料,母岩为弱风化中厚层块状泥晶生物灰岩,成分主要以碳酸盐为主,含少量白云岩,原岩抗压强度为61.16 MPa,颗粒相对密度ρr为2.72。压缩模量为104.2 MPa,含水量为0.05%。原级配最大粒径为600 mm,级配曲线见图1。侧限压缩试验采用的仪器是重庆交通大学与江苏永昌科教仪器制造有限公司联合研制的三联式单向压缩试验仪,位移传感器精度0.001 mm,竖向应力通过组合不同的砝码施加,最大应力为2.0 MPa。侧限压缩试验采用直径为100、150、200 mm的压缩桶,控制高宽比为1。试验采用分级加载的方式,调节砝码控制加载等级为50、100、200、400、800、1 600 kPa,当试样在某一压力等级下的每小时变形量不超过0.005 mm时视为变形稳定,变形稳定后加载至下一压力等级。待最后一个压力等级加载结束后对试样进行筛分试验。

图1 级配曲线

控制试样最大粒径为20 mm时,试样缩尺方法采用混合法和相似级配法,相似级配法缩尺后的级配为级配1,其中控制混合法中的缩尺比为3、5、7、9,对应级配2—级配5。控制缩尺方法相同,试样最大粒径为40、20、10 mm,对应级配6、级配4、级配7。缩尺后各级配曲线见图1。结合研究目的制定具体试验方案见表1,每种级配的特征参数见表2。

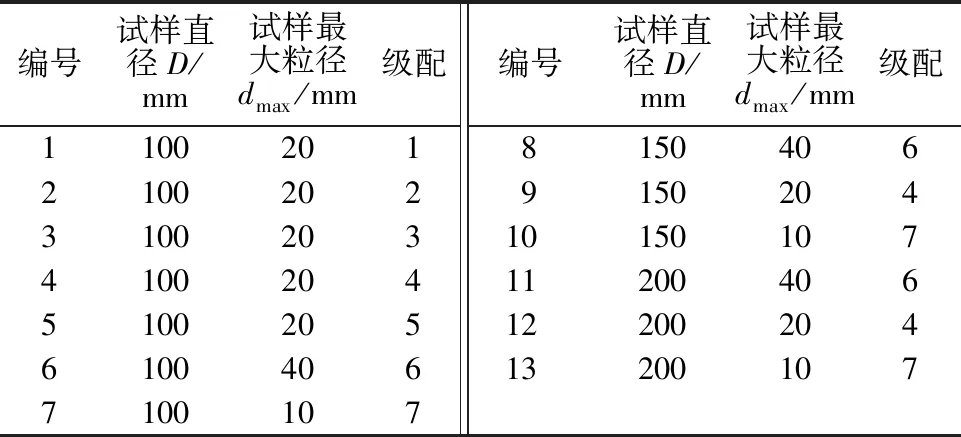
表1 试验方案

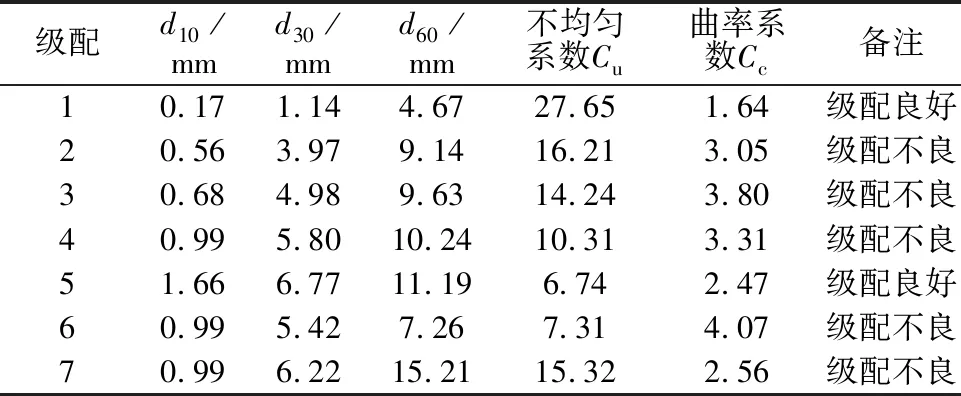
表2 各级配特征参数

2 缩尺效应对堆石料压缩特性的影响

2.1 缩尺方法对堆石料压缩特性的影响

P5含量指的是级配中>5 mm颗粒物的百分含量,在研究中常将其称为粗颗粒含量。马捷等[7]对级配最大粒径相同、级配组成不同的若干组粗粒土试样开展了压缩试验,研究了压缩系数对P5含量影响的变化规律。蔡国军等[8]研究了不同级配条件下土石混合体的强度特性,内摩擦角随着P5含量的增大呈现先增大后减小的趋势。结合相关研究发现,在级配最大粒径相同的条件下,P5含量能够反映级配曲线的部分特征,因此将P5含量作为级配曲线的一个特征因子,对通过不同缩尺方法得到的试样压缩性进行讨论。

图2为试样直径为100 mm时的土体e-p关系曲线图,试样直径为150、200 mm时所呈现的变化趋势与之相同。根据压缩系数的定义可知,土体e-p曲线上某一点的斜率能够反映此处土体沉降的速率,由此评价土的压缩性能。由于土的压缩曲线在使用函数描述方面还存在一些关键问题,在工程运用中,通常用曲线上临近两点割线的斜率近似表示这一段土体的压缩速率。用这种方法求得的不同压力级别下的压缩系数和P5含量关系曲线如图3所示。

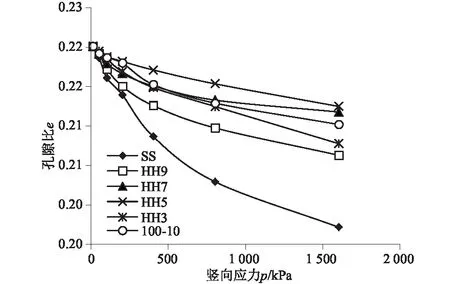
注:SS表示缩尺方法为相似级配法;HHx表示混合法,其中x为缩尺倍数;100-10表示试样直径为100 mm,试样最大粒径为10 mm。

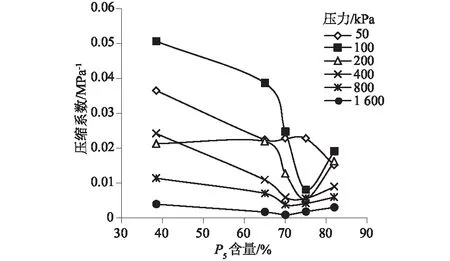
图3 压缩系数与P5含量关系曲线

由图3可得,试样的压缩系数与P5含量之间存在一定的关系:在同一压力等级下,压缩系数随着粗颗粒含量的增加大致呈现“V”型发展趋势,即压缩系数在本文研究的压力范围内存在一个最小值。压力等级为100 kPa时,曲线上压缩系数的最小值在P5含量75%处,随着压力等级的提高,曲线上压缩系数的最小值向P5含量减小的方向发生偏移。竖向压力提高至1 600 kPa时,压缩系数在P5含量70%处取得最小值。此外,压缩系数与P5含量关系曲线的斜率表示压缩系数随着粗颗粒含量变化的速率,据此将压缩曲线划分为3个阶段。第一阶段在100 kPa压力等级时,压缩系数在P5含量由40%增值60%的过程中下降缓慢。第二阶段在P5含量由60%增至75%的过程中,压缩系数的变化速率较前一阶段大幅上升。第三阶段在P5含量由75%继续增大时,为压缩系数回升阶段,曲线的斜率与第二阶段斜率的绝对值接近。这一现象同样受到竖向压力的影响,第一、二阶段曲线斜率的差值随着竖向压力的提高而减小,竖向压力1 600 kPa时,压缩系数和P5含量关系曲线演化为一条关于轴线P5含量为70%对称的折线。

级配中的粗颗粒在试样中承担骨架作用,细颗粒填充于骨架间的空隙中,从而形成一个试样整体。在粗颗粒含量增加的过程中,试样中的细颗粒含量逐渐填充骨架间的空隙部分,直到细颗粒能够完全填充粗颗粒空隙,试样整体达到最密实的状态[9-10]。在这个过程中,越来越多的细颗粒参与到骨架的构成中来,而颗粒的抗拉强度随着粒径的减小而增大,因此骨架中细颗粒含量的增加可以提高试样整体抵抗变形的能力,对应图3中P5含量增加时,压缩系数与P5含量关系曲线首先出现下降的趋势,在达到试样最密实状态时,变形量相应达到最小值。继续增大粗颗粒料的含量,细颗粒料不足以填充这种空隙,导致填充效果下降,对应图3曲线中的上升部分,P5含量>75%时,试样的竖向变形随着粗颗粒含量的增加呈增大趋势。当压力等级较低时,外部荷载不能克服颗粒间的摩擦阻力,产生的竖向变形量较小且不随颗粒级配的改变产生大范围的波动。

2.2 试样最大粒径对堆石料压缩特性的影响

将150-10、150-20、150-40(150表示试样直径为150 mm,10、20、40表示试样最大粒径(mm))试验组数据绘于试样最大粒径-压缩系数坐标系中,如图4所示。

图4 压缩系数与试样最大粒径关系曲线

根据图4可知,在试样直径为150 mm的试验组中,竖向压力为50 kPa时,压缩系数随试样最大粒径的波动较大,其余竖向压力等级下,堆石料的压缩系数随着试样最大粒径的增大呈规律性的变化。当试样最大粒径由10 mm增大至20 mm时,不同竖向压力下的压缩系数有不同程度的上升,当试样最大粒径由20 mm增至40 mm时,竖向压力1 600 kPa条件下,压缩系数呈减小趋势,其余竖向压力下压缩系数呈上升趋势。若以试样最大粒径-压缩系数曲线斜率的大小表示压缩系数受试样最大粒径的影响程度。从总体上看,试样最大粒径10 ～20 mm段,压缩系数受试样最大粒径的影响较大,试样最大粒径20 ～40 mm段,压缩系数受试样最大粒径的影响较小。

2.3 试样直径对堆石料压缩特性的影响

分析最大粒径为20 mm时的3组数据,得到试样的压缩系数随着试样直径的变化趋势,如图5。

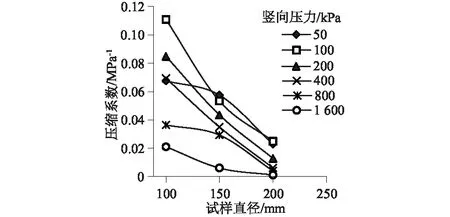
图5 压缩系数与试样直径关系曲线

根据图5可知,当试样级配曲线相同时,随着试样直径的增加,压缩系数随之发生显著变化。试样最大粒径相同的条件下,均表现出压缩系数随着试样直径的增大而减小的趋势。当dmax=20 mm时,不同竖向压力下试样直径与压缩系数近似线性函数关系,且直线斜率随着竖向压力的上升而降低。当dmax=20 mm时,除了竖向压力为50 kPa和800 kPa的情况,试样直径由100 mm增至150 mm压缩系数的减小量要高于试样直径由150 mm增至200 mm压缩系数的减小量。认为在试验研究的尺寸范围内,压缩系数的变化率随着试样直径的增大而降低。陈坚等[11]在研究了径-径比对灰岩颗粒料干密度的影响后发现,当径-径比>6.8时,干密度随着径-径比的增大趋于稳定,当径-径比<6.8时,干密度随着径-径比的增大显著增大。在上述试验组中,试样直径由100 mm增至200 mm的过程中,对应径-径比由5增至10。当径-径比由5增至6.8时,试样干密度的变化幅度较大,压缩系数随之发生明显变化,当径-径比由6.8增至10时,试样干密度趋于稳定,压缩系数的变化速率低于前一阶段。

3 缩尺效应对堆石料颗粒破碎的影响

3.1 粗颗粒含量P5对堆石料颗粒破碎的影响

材料的颗粒破碎指标按照其计算方法可以分为三类:第一类是以单个或多个特征粒径的变化来反映颗粒破碎程度,第二类是以各粒组破碎前后质量的变化表示颗粒破碎程度,第三类是定义与级配曲线相关的破碎势,通过研究破碎前后级配曲线的变化求出颗粒的破碎耗能,以此计算破碎率。其中由Hardin[12]提出的基于破碎势建立的颗粒破碎指标Br被广大学者证实能够很好地描述材料的颗粒破碎过程。按照Hardin等人的理论,大粒径的颗粒最后都会破碎成d=0.074 mm的细颗粒。EINAV[13]等则认为颗粒破碎的过程存在一个限度,发生破碎后的级配曲线趋向于一个极限级配,以极限级配曲线作为计算破碎势能的积分上限更符合实际的颗粒破碎情况,基于此提出了颗粒破碎率BE。郭万里等[14]认为BE描述颗粒破碎程度的实质是颗粒发生破碎消耗的势能与一个同量纲的定值相除,得到了修正后的颗粒破碎指标相对破碎率BW。

(1)

式中:Sa为初始级配曲线与试验后级配曲线围成的面积;Sb为初始级配曲线与d=dmax和横坐标轴围成的面积。

颗粒的相对破碎率随着竖向荷载的增大而增加,并且增长速度随着竖向荷载的增大而减缓。刘萌成等[15]研究了珊瑚礁钙质砂侧限压缩下的颗粒破碎特性,颗粒相对破碎率与竖向荷载间的关系颗粒用幂函数表示为

(2)

式中:b1、c1为相关参数;σv为竖向荷载;Pa为标准大气压,公式拟合情况见图6。

经试验结果得到P5含量与b1、c1的关系如图7所示。

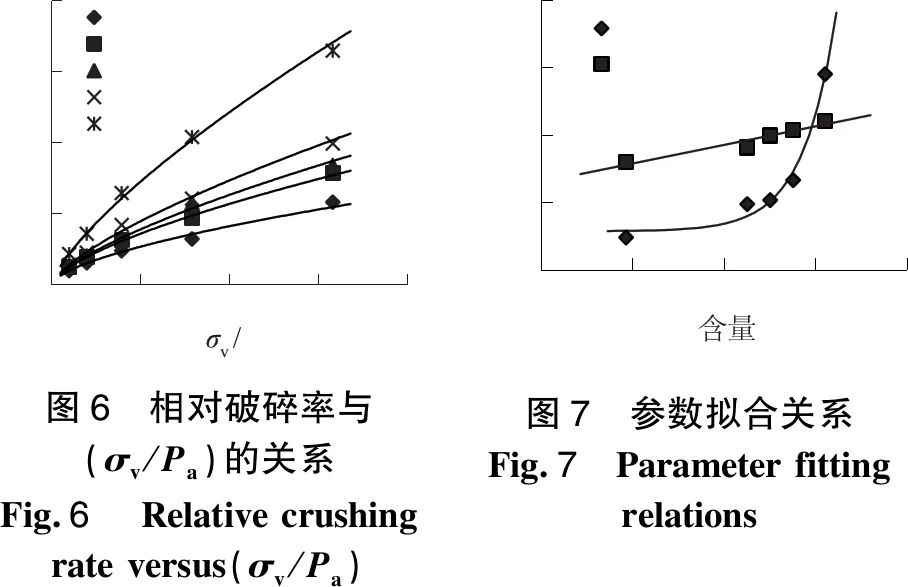
由图7可知b1与P5呈指数关系,c1与P5含量呈线性关系,拟合式如下:

b1=d1ef1P5+g1;

(3)

c1=h1P5+j1。

(4)

式中:d1、f1、g1为拟合参数,R2=0.966;h1、j1为拟合参数,R2=0.927。将式(3)和式(4)代入式(2)中,可得考虑缩尺方法对粗颗粒含量影响的颗粒破碎率演化方程为

(5)

式中d1、f1、g1、h1、j1为拟合参数,取值同上。

3.2 试样最大粒径对颗粒破碎的影响

以试样最大粒径dmax为横坐标,相对破碎率BW为纵坐标,得到相对颗粒破碎率与试样最大粒径的关系曲线(图8)。

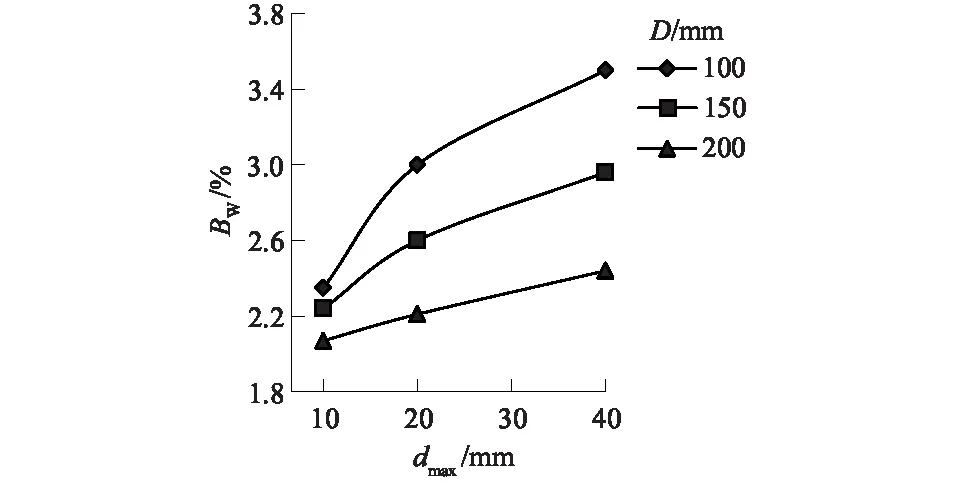
图8 相对破碎率与试样最大粒径关系

根据图8可知,试样的相对破碎率与试样最大粒径有关,随着试样最大粒径的增大,试样的相对破碎率相应也随之增大。本文进行试样最大粒径对堆石料压缩特性的影响时保证了制样方法相同,即均采用混合法,先将原级配等比例缩尺后根据最大粒径的不同再进行等量替代。由相对破碎率BW的定义可知,级配曲线与最大粒径线和坐标横轴所围成的面积表示颗粒破碎的势能。随着级配曲线中最大粒径的增加,围成的面积也相应地增大,即具有更高的破碎势能,容易发生颗粒破碎,相较于小粒径颗粒,大粒径颗粒更易发生颗粒破碎。图8中曲线的斜率表示相对破碎率随着最大粒径变化速率的快慢,显然,在试样直径为100 mm时,相对破碎率随着试样最大粒径增大的变化速度较快,随着试样直径的增大,破碎率-试样最大粒径曲线的斜率有所降低,表示随着试样直径的增大,试样最大粒径对相对破碎率的影响减弱。

3.3 试样直径对颗粒破碎的影响

同样的,以试样直径D为横坐标,相对破碎率BW为纵坐标,得到相对破碎率随着试样直径的变化曲线,如图9。

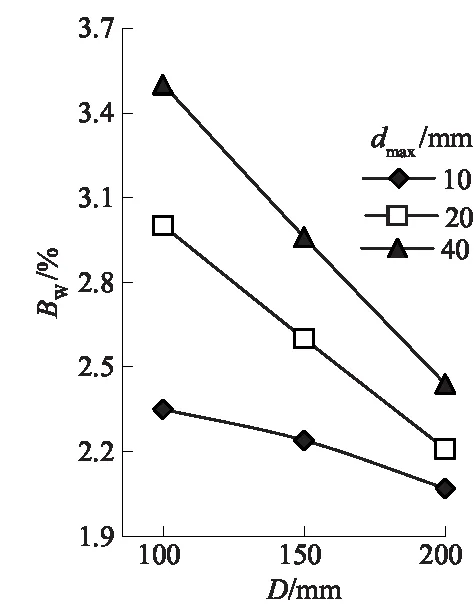
图9 相对破碎率与试样直径关系

根据图9可知,试样的相对破碎率与试样直径有关,当试样最大粒径相同时,相对破碎率随着试样直径的增大而减小。朱俊高等[16]研究了试样直径对粗粒土三轴剪切特性的影响后发现,试样最大粒径相同的条件下,小直径试样的体积应变和颗粒破碎率都低于大尺寸试样,产生这种差异的原因是试样的加载方式不同。三轴剪切试验时,不同尺寸试样的端部约束条件不同,并且大尺寸试样在制样过程相较小尺寸试样更容易产生不均匀区,使局部区域的强度不能完全发挥,导致颗粒破碎,压缩变形量增大。侧限压缩试验限制了试样在侧方向上的变形,与三轴加载相比没有围压σ3这一影响条件,弱化了试样直径对端部约束的影响。正是因为侧限压缩试验只反映在竖向加载方向上的变形,侧壁与试样的接触情况成为影响变形的主要条件,随着试样直径的增大,更多的颗粒与侧壁接触,侧壁摩擦增大。在竖向压力相同时,因为侧壁摩擦的存在,小尺寸试样的有效竖向压力大于大尺寸试样,表现为随着试样直径的增大,相对破碎率减小。关于由试样直径增大引起的产生不均匀区的可能性增大的问题,可以通过开展平行试验取平均值,从而将误差控制在一定的范围内。

将以上数据置于ORIGIN软件中拟合得到三维曲面图,如图10。

图10 相对破碎率曲面

由图8和图9可知,相对破碎率与试样最大粒径之间呈对数函数关系,与试样直径之间也呈对数关系,据此可以将相对破碎率BW表示为试样最大粒径dmax和试样直径D构成的函数,BW=f(dmax,D)。经拟合得到曲面的函数表达式为

BW=b2lnDlndmax+ln(dmaxc2Dd2)+f2。

(6)

式中:b2、c2、d2、f2为拟合参数,b2取-0.809,c2取4.559,d2取1.409,f2取-6.021。

3.4 缩尺效应对颗粒破碎影响的讨论

根据图10可知,在试样直径和试验最大粒径构成的坐标系中,相对破碎率为一个空间曲面,由式(5)可得,在试样直径和试样最大粒径不变时,试样的相对破碎率随着竖向荷载的增加而单调递增。图10为竖向荷载为1 600 kPa时对应的颗粒破碎曲面,荷载低于1 600 kPa的颗粒破碎曲面在上述曲面的下方,且随着竖向荷载的减小而朝着原点方向移动,同样的,荷载高于1 600 kPa的颗粒破碎曲面在上述曲面的上方。为了使式(6)能够反映竖向压力对颗粒破碎率的影响,结合式(5)对其进行修正

BW=b2lnDlndmax+ln(dmaxc2Dd2)+

(7)

于际都等[17]利用染色石膏颗粒研究散粒材料的颗粒破碎规律,对不同初始级配的试样开展侧限压缩试验,按照式(5)计算800 kPa和1 600 kPa时的颗粒破碎率BW为2.474%和4.971%。将dmax、D、σa代入式(7)中,得到颗粒破碎率理论计算值为2.302%和4.702%。比较可得,理论计算值低于实测值,但总体相差不大。魏浩等[18]对5种不同级配的粗粒料利用大型压缩试验仪开展了压缩破碎特性试验,试样直径为Φ300 mm×150 mm,最大荷载为2 000 kN。原文中试样5对应的试样最大粒径为20 mm,且试样级配与本文中级配3相似,若将D=300 mm,dmax=20 mm代入式(7)中,计算得到竖向荷载为2 000 kPa时的相对破碎率为3.21%,原文中竖向荷载为2 000 kPa时的颗粒破碎率BW为5.02%。

式(7)是根据式(6)在竖直方向平移得到的,即认为不同竖向压力条件下,试样直径和试样最大粒径对颗粒破碎的影响规律是一致的。由上述验证结果可知,式(7)仅在试样直径和试样最大粒径一定范围内适用,超出这一范围后对颗粒破碎描述的准确性下降,说明不同压力条件下,试样直径和试样最大粒径对颗粒破碎的影响存在差异。在讨论式(6)对不同压力等级的适用性时,需要从参数b2、c2、d2入手,分别研究压力等级与试样直径、压力等级与试样最大粒径对颗粒破碎的共同作用。研究不同压力等级下,试样直径和试样最大粒径对颗粒破碎的影响涉及大量的试验组,工作量较大,本文并未涉及相关研究,仍需要进一步开展试验研究。

4 结 论

通过对不同缩尺方法、不同试样最大粒径、不同试样直径的试样开展侧限压缩试验和颗粒筛分试验,研究了尺寸效应对堆石料压缩特性和颗粒破碎特性的影响。

(1)堆石料的压缩系数受缩尺方法影响显著,不同缩尺方法导致试样中粗颗粒含量发生变化,压缩系数随着粗颗粒含量的上升呈先降低后增加的趋势。压缩系数随着试样最大粒径的增加而增大,随着试样直径的增大而降低。

(2)堆石料的相对颗粒破碎率随着试样中粗颗粒含量的上升而增大,可以用幂函数描述两者间的对应关系。颗粒破碎率随着试样最大粒径的增大而增大,随着试样直径的增大而减小。在缩尺方法相同时,相对破碎率与试样最大粒径和试样直径间的关系可以表示为一个空间曲面。讨论了空间曲面表达式对不同压力等级下颗粒破碎程度的适用性,在试样直径和最大粒径超出一定范围后对颗粒破碎描述的准确性下降,需要进一步开展试验研究。