HBV模型在玛纳斯河流域的适用性

张海川,尤 洋,乔长录,王 斌

(1.石河子大学 水利建筑工程学院,新疆 石河子 832000;2.现代节水灌溉兵团重点实验室,新疆 石河子 832000;3.第八师石河子市水利工程管理服务中心,新疆 石河子 832000)

0 引 言

在我国西北干旱区,以新疆天山北坡河流为代表的流域,山区的冰雪融水和降雨是山前平原径流的主要来源,占年径流量的80%以上,冰雪融水的补给比例可达36%[1]。因此,冰雪融水和降雨对当地人民的生产、生活以及环境有着决定性的作用[2]。在天山的高寒地区,由于地形条件复杂,流域内水文气象监测站点稀少,难以取得气象要素的时空变化特征[3]。尽管部分学者进行了相关研究,但是受基础数据的限制,对该地区水文规律的认识依然不足。

水文模型是探究水文规律的有力工具[4]。对于融雪径流模拟,国内外应用比较广泛的有SWAT(Soil and Water Assessment Tool)模型[5-7]、HBV(Hydrologiska Byråns Vattenbalansavdelning)模型和SRM(Snowmelt Runoff Model)[8-10]等,其中HBV模型与SRM都具有所需驱动数据少、模拟效果好的优点,适用于资料稀缺流域的融雪径流模拟[11-12]。HBV模型是瑞典气象和水文局(Swedish Meteorological and Hydrological Institute,SMHI)针对瑞典寒区流域开发的半分布式水文预报模型,在融雪对径流补给作用明显的流域有较强的适用性[13],在国内外均取得了良好的应用效果。Montero等[14]运用HBV模型对土耳其的Karasu流域以及德国的Nahe和Main流域的径流进行模拟,研究发现多源气象资料可用于驱动HBV模型。谷一等[15]对不同降雨数据资料条件下HBV模型在逊毕拉河流域的适用性进行了评价,结果表明:4个典型流域率定期和验证期的NSE(Nash-Sutcliffe Efficiency)系数多在0.6以上,HBV模型在逊毕拉河流域的适用性较好。高胖胖[16]耦合多气候情景(Multi-Global Climate Models,MGCM)和HBV模型,分析气候变化对阿姆河流域未来径流变化的影响。研究表明该模型不仅能减少由全球气候模式(Global Climate Model,GCM)的异质性带来的不确定性,而且适用于分析以冰川和融雪产流为主的阿姆河流域的径流变化。

SRM是一种基于度日因子的概念性水文模型,主要用于模拟预报以融雪径流为主的山区流域日径流过程。该模型在新疆天山地区以及玛纳斯河流域已有广泛的应用。穆艾塔尔·赛地等[1]利用SRM对天山北坡的乌鲁木齐河、奎屯河和玛纳斯河的融雪径流进行了模拟,并对模拟结果和模型有效性进行了检验,结果表明3个流域相关系数R2平均值和径流体积差Dv平均值分别为0.78和9.19%,SRM在新疆天山北坡山区流域的径流模拟中具有良好的适用性;张璞等[17]使用中国气象局T213数值产品驱动SRM对玛纳斯河流域2004年的春季融雪径流进行了预报,结果表明流域3 d径流量预报评价指标相关系数R2=0.87,径流体积差Dv=-4.9%,达到了较好的预报效果。

HBV模型相较SRM无需流域每日积雪覆盖率数据进行驱动,更适用于无资料地区的径流模拟,且其包含的土壤水分模块相比SRM能更全面地反映流域真实产汇流情形。但相对于SRM的广泛应用,HBV模型在新疆天山地区应用较少,所以本文通过对比分析HBV模型和SRM在资料稀缺的玛纳斯河流域的径流模拟效果,研究HBV模型在新疆天山北坡山区流域的适用性,以期为中国西北高寒区流域径流模拟提供一定参考。

1 研究区概况与数据来源

1.1 研究区概况

本文研究区域为新疆玛纳斯河流域肯斯瓦特水文站以上流域,玛纳斯河流域地处85°01′E—86°32′E,43°07′N—45°21′N,南起依连哈比尔尕山,北接古尔班通古特沙漠,西临巴音沟河,东至塔西河,汇集了包括清水河等在内的十多条支流。玛纳斯河是流域内最大的一条河流,全长约324 km[18]。肯斯瓦特水文站测站海拔900 m,是玛纳斯河流域的出山口控制站,控制流域面积4 637 km2[19],该站多年平均气温6.4 ℃,多年平均降水量为340.8 mm。

1.2 数据来源

针对研究区域,收集研究所需的气象、水文、数字高程模型(Digital Elevation Model,DEM)和积雪数据等。

(1)气象数据。研究区内没有传统气象站点,肯斯瓦特水文站作为研究区内唯一的位于流域出山口的控制站,海拔为900 m,远低于研究区3 254 m的平均海拔。由于垂直气候带的作用,水文站的气象数据无法直接用于中高海拔山区的径流模拟,研究区缺乏必要的历史气象资料[20],所以本文使用的降水和气温数据分别为中国气象数据网(https:∥data.cma.cn)公布的中国地面降水日值0.5°×0.5°格点数据集(V2.0)(以下简称降水格点数据集)、中国地面气温日值0.5°×0.5°格点数据集(V2.0)(以下简称气温格点数据集)。数据集是基于我国2 472个气象站的气象数据,运用地理空间技术与薄盘样条插值法,得到分辨率均为0.5°×0.5°的降水和气温数据集[21],相比众多全球范围的降水与气温数据,该数据集对中国地区更有针对性。数据集经验证与误差分析,质量状况良好[22-23]。潜在蒸散发数据采用中国科学院地理科学与资源研究所地球数据科学与共享研究室提供的全球0.5°逐月潜在蒸散发数据集(2000—2013年)。

(2)流量数据。本文所用到的肯斯瓦特水文站流量数据来自石河子市水利工程管理服务中心,选取2000—2013年实测日平均流量数据,多年平均径流量及各月平均流量用于径流模拟的校准。

(3)DEM数据。选用来自地理空间数据云平台(http:∥www.gscloud.cn)分辨率为90 m×90 m的SRTM_DEM数据进行地理信息的提取。

(4)积雪数据。数据采用国家冰川冻土沙漠科学数据中心(http:∥www.ncdc.ac.cn)提供的2000—2013年MODIS(Moderate-resolution Imaging Spectroradiometer)北半球逐日无云二值积雪产品。该产品利用每日积雪分类产品数据MOD10A1、MYD10A1和AMSR-E每日雪水当量产品数据,运用最大积雪面积融合法,得到分辨率为500 m×500 m北半球逐日无云二值积雪图像。对合成的最终逐日积雪图像精度分析表明,陆地和积雪分类一致性分别为92%和87.1%,总体分类精度达到90.7%[24]。

2 模型构建及气象数据处理

2.1 积雪与径流相关性分析

通过ArcGIS软件先对2000—2013年逐日积雪影像进行裁剪,再对研究区逐日积雪覆盖面积进行叠加,得到多年月平均积雪覆盖面积变化过程(图1)。通过分析2000—2013年多年月平均积雪覆盖率与多年月平均流量的变化过程(图2(a))以及相关关系(图2(b)),研究玛纳斯河流域积雪与径流的相关性。

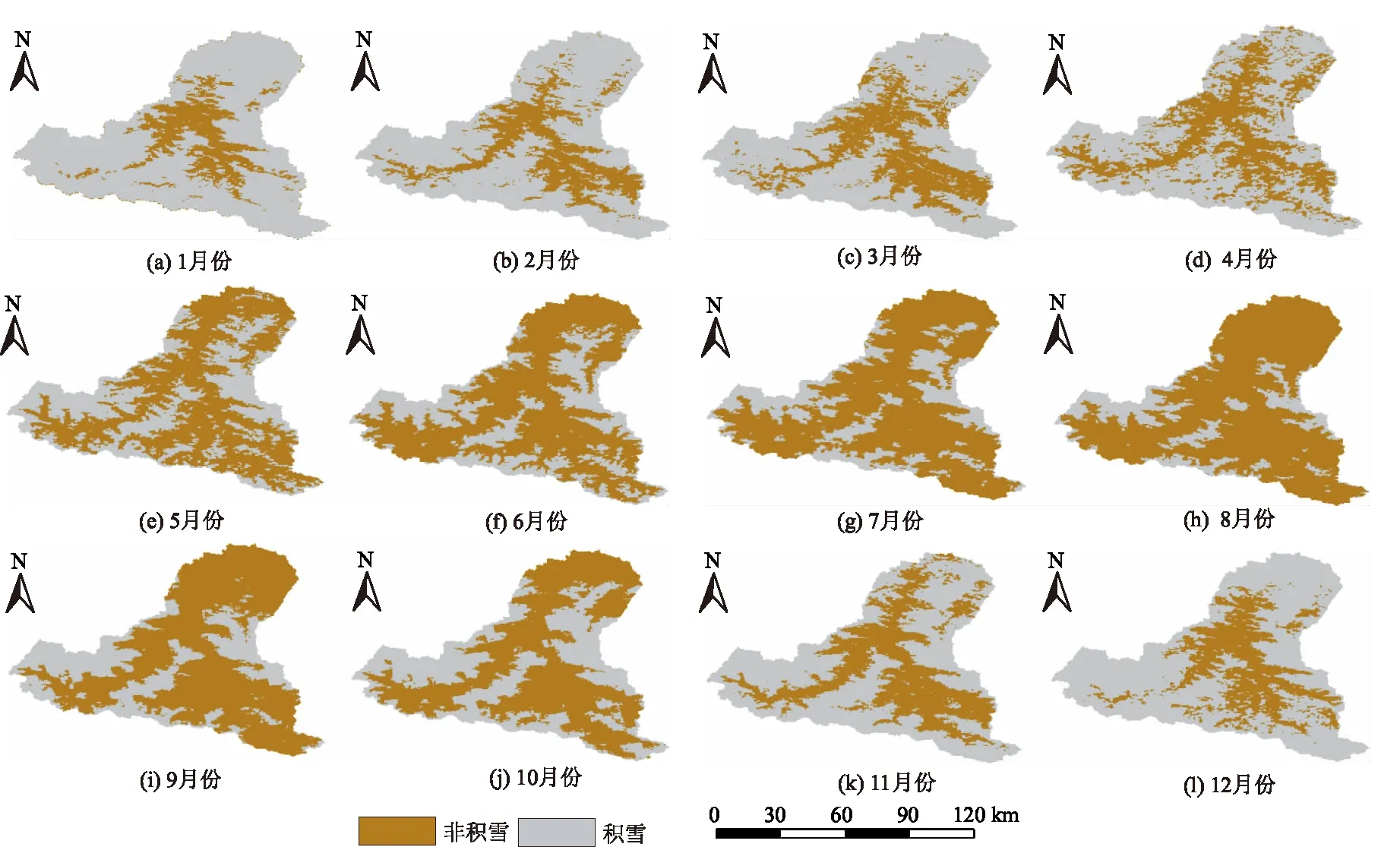
图1 2000—2013年多年月平均积雪覆盖面积变化过程

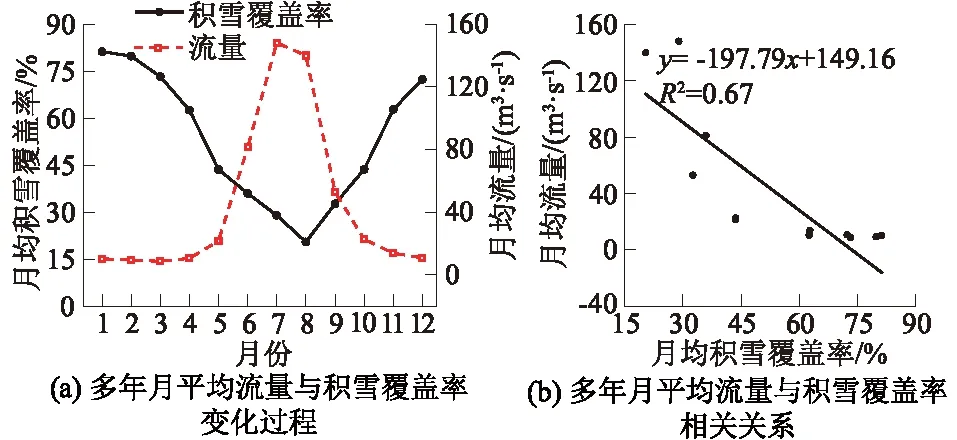
图2 2000—2013年多年月平均流量与积雪覆盖率变化过程和多年月平均流量与积雪覆盖率相关关系

从图1和图2(a)可以看出研究区从3月份开始快速融雪,到8月份积雪覆盖面积达到最小,最小积雪覆盖率为20.5%,除了高海拔区域的常年积雪,其它区域基本不存在积雪。9月份随着山区温度降低,积雪面积开始增加,到次年1月份达到最大,最大积雪覆盖率为81.2%。由图2可知,积雪覆盖率和多年月平均流量呈负相关,多年月平均流量在7、8月份达到峰值,而此时积雪面积为最低值,从11月份到次年4月份的非汛期,积雪覆盖率在62.5%以上。月平均积雪覆盖率与流量的相关系数R2=0.67,表明玛纳斯河流域积雪融水对径流的补给作用明显。流域水文条件决定了以融雪径流模拟为主的HBV模型和SRM模型可以在该流域应用。

2.2 模型构建

2.2.1 HBV模型构建

HBV模型以降水、气温、径流和潜在蒸散发作为基本输入值,主要由融雪模块、土壤水分模块、产流模块和汇流模块4部分组成。HBV模型采用水量平衡原理,其定义的水量平衡方程式为

(1)

式中:P为降水量(mm);R为径流量(mm);E为蒸散发量(mm);SC为积雪覆盖量(mm);SW为土壤含水量(mm);UZ为浅层地下水量(mm);LZ为深层地下水量(mm);Lakes为流域所有水体的水量(mm)。

在HBV模型的流域设置中,可以将流域分为不同的子流域,分别计算每个子流域的日径流量,再将各个子流域产生的日径流量进行叠加。使用ArcGIS软件中的水文分析工具结合研究区的DEM数据,将研究区分为17个子流域(图3),并提取出每个子流域中心点的经纬度和海拔数据(表1)。由于玛纳斯河上游山区面积较小,各子流域几何中心点具有一定代表性[25],因此本文以子流域几何中心点的气象数据代表相应子流域的气象数据。

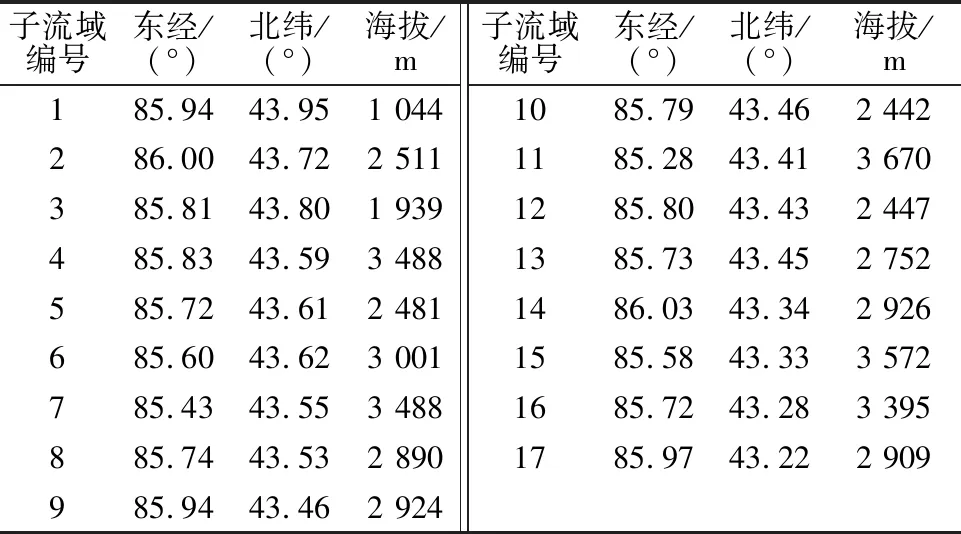
表1 各子流域中心点数据

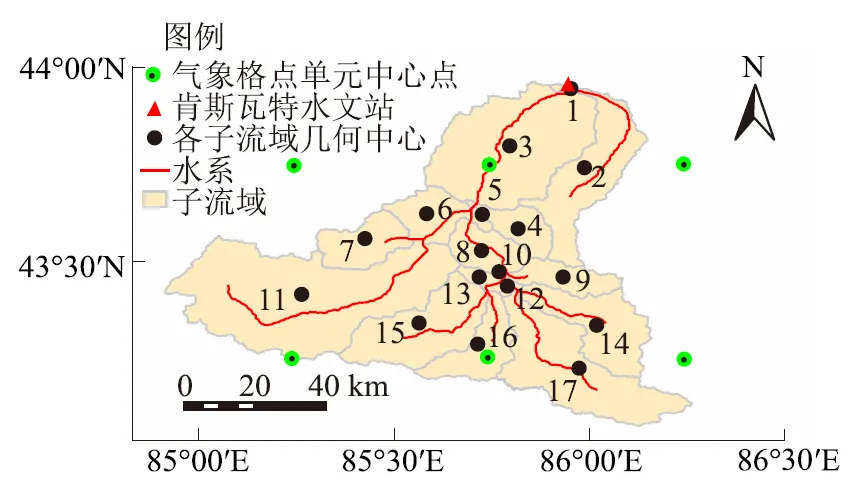
图3 子流域和气象格点示意图

2.2.2 SRM模型构建

SRM模型的基本输入变量为日降水量、日气温、和日积雪覆盖率,原理是分别计算每天的融雪和降水量,得到逐日流量,产流计算公式为

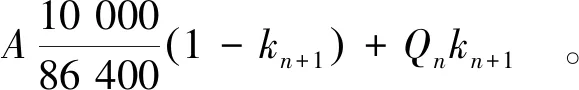
(2)

式中:Q为日平均流量(m3/s);CRN和CSN分别为降雨径流系数和融雪径流系数;P为日降雨量(cm);α为度日因子(cm/(℃·d));T和ΔT分别为气温度日因子数和气温递减值度日因子数(℃·d);S为积雪覆盖率;A为流域分带面积(km2);k为径流退水系数;10 000/86 400为单位换算系数;下标n和n+1分别代表第n日和第n+1日。

根据SRM模型使用手册,当流域海拔超过500 m时,需要对流域进行分区处理,分别计算每个分区的日径流量,再将各个分区产生的日径流量进行叠加,研究区的海拔范围为857～5 135 m,按照每隔500 m为1个分区,将其划分为8个分区(表2)。

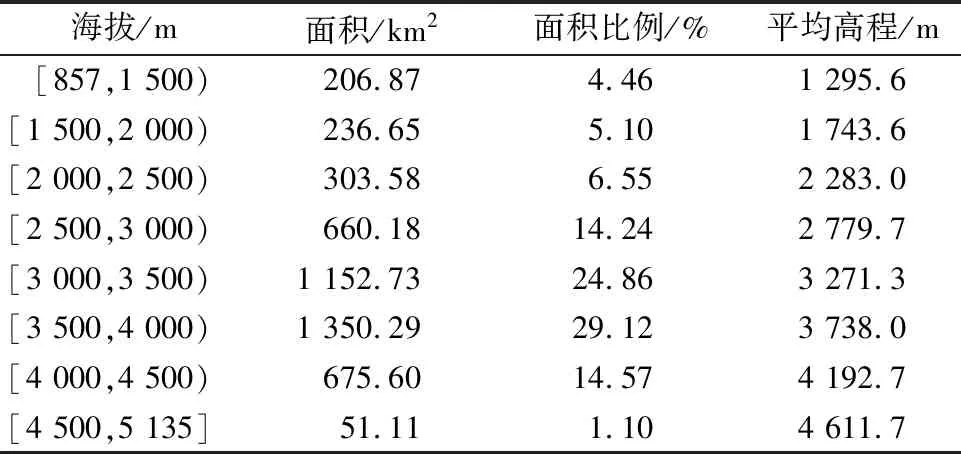
表2 研究区各海拔分区范围、面积及平均高程

2.2.3 模型评价指标

本文选取Nash-Sutcliffe系数NSE、相对均方根误差(RMSE-observations Standard Deviation Ratio,RSR)和百分比偏差(Percentage Bias,PBIAS)为模型适用性评价指标。NSE系数有NSE和lg(NSE)2种,NSE对峰值流量更敏感,lg(NSE)对低流量更为敏感[26]。Singh等[27]提出的RSR表示模拟值与相应实测值的离散程度,RSR由实测值标准差(Standard Deviation,STDEVobs)将均方根误差(Root Mean Square Error,RMSE)标准化得到。PBIAS表示模拟值的平均趋势相对实测值平均趋势的偏离程度[28]。计算公式分别为:

(3)

lg(NSE)=

(4)

(6)

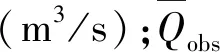
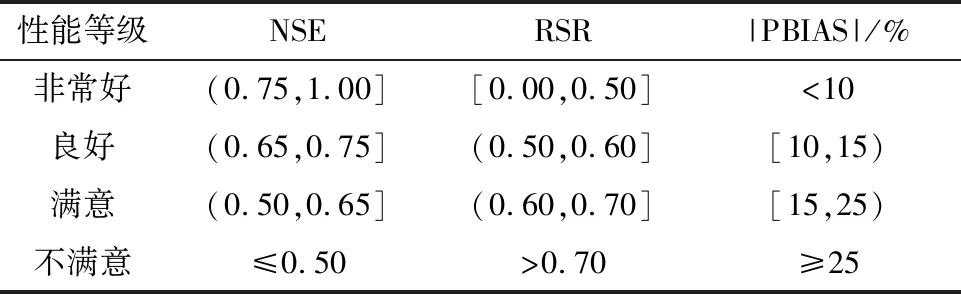
表3 评价指标性能等级分类标准

2.3 降水与气温数据空间插值

为揭示降水和气温格点数据的空间分布情况,本文基于气象格点2000—2013年多年平均降水和气温数据,采用ArcGIS软件地统计分析模块中考虑DEM高程数据的协同克里金插值法得到研究区多年平均降水量(图4(a))和气温(图4(b))的空间分布数据。

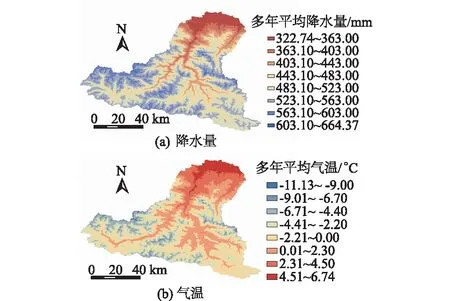
图4 研究区多年平均降水量空间分布和多年平均气温空间分布

从图4可知,研究区降水量从东北到西南方向随高程递增,从流域出山口到高山区,降水量由322.74 mm增加到664.37 mm;气温从东北到西南方向随高程递减,从流域出山口到高山区,气温由6.74 ℃降低到-11.13 ℃,研究区多年平均降水和气温空间分布情况与有关学者研究结果[31-32]基本一致。有关研究表明研究区多年平均降水量500 mm[33],多年平均气温-2 ℃[34],对空间分布数据计算得到研究区多年平均降水量473.56 mm、多年平均气温-1.63 ℃,格点数据集对研究区的降水存在低估,对气温存在高估。

为增强气象格点数据的空间代表性,削弱中高海拔垂直气候带的影响,本文利用各子流域中心点的经纬度由空间分布提取出各点的多年平均降水和气温数据,利用气象格点和子流域中心点的多年平均降水和气温数据,参考先前学者的研究[35-37],计算出各海拔区的降水每百米增加值(Precipitation Correction Altitude-gradient,PCALT(mm/hm))和气温每百米降低值(Temperature Correction Altitude-gradient,TCALT(℃/hm)),见表4。根据式(7)和式(8)分别对SRM不同海拔区和HBV模型处于不同海拔区的子流域中心点的日平均降水和气温数据分梯度进行修正,修正数据对于SRM作为对应海拔区的气象数据输入模型,对于HBV模型作为对应子流域的气象数据输入到模型子流域文件中。

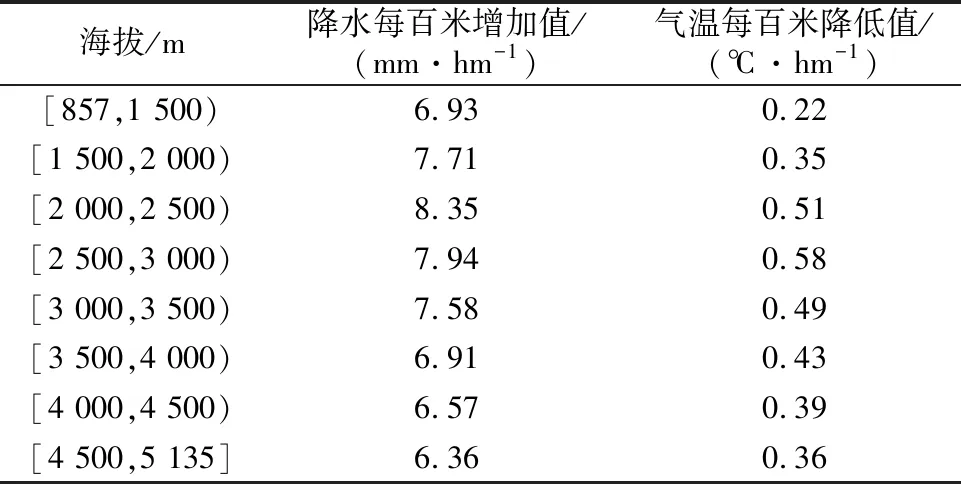
表4 各海拔区降水和气温每百米变化梯度

(7)

(8)

式中:h为各分区平均海拔或各子流域中心点海拔(m);h0为气象格点相应的海拔(m);P(h)和P0分别为相应海拔处的降水量(mm);T(h)和T0分别为相应海拔处的气温(℃)。

3 结果与分析

3.1 模型参数率定结果

HBV模型主要有15个参数,为了更有针对性地调整参数,需要对参数进行敏感性分析。本文首先利用蒙特卡罗模拟(Monte Carlo Simulation)对参数自动率定,再根据参数的实际物理意义和敏感性,将不敏感的参数调整到合理范围内,选取较敏感的10个参数采用遗传算法多次迭代运算得到参数最佳值(表5)。SRM在玛纳斯河流域应用广泛,本文参考穆艾塔尔·赛地[1]、王晓杰等[38]、宁理科等[39]对SRM在玛纳斯河流域的应用研究,确定出SRM参数率定的范围(表5),并在模拟过程中根据模拟效果在给定范围内进行调整,其中退水系数公式为

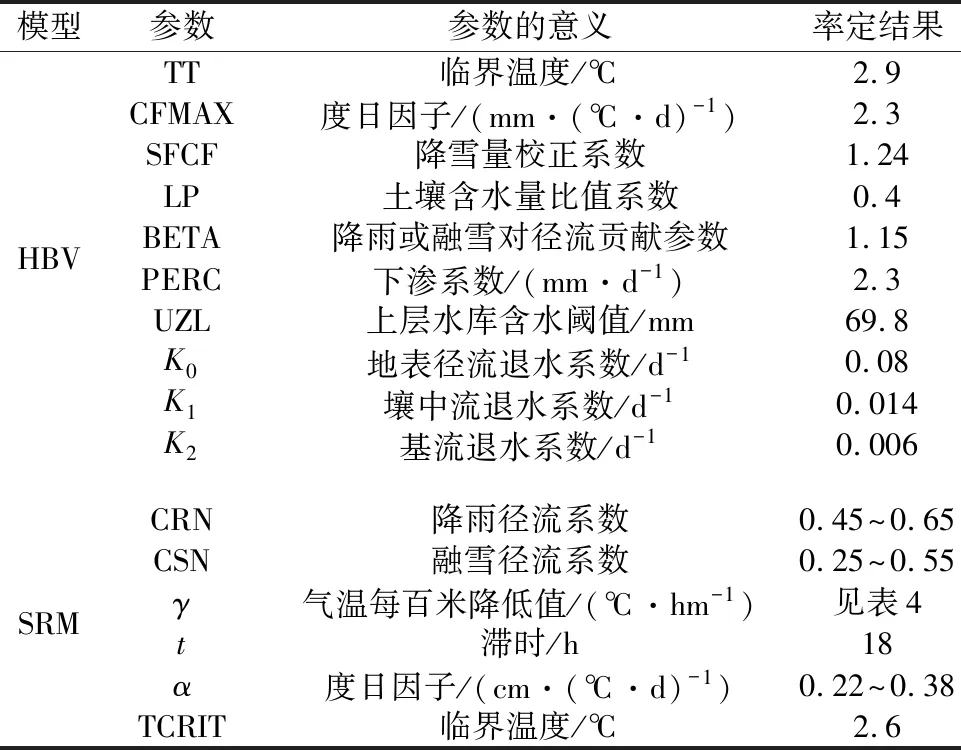
表5 模型参数率定结果

(9)

式中:Qn为第n日平均流量;kn+1为第n+1日退水系数。

3.2 径流模拟结果对比分析

为验证HBV模型在玛纳斯河流域的适用性,本文分别运用HBV模型和SRM对研究区2000—2013年日尺度和月尺度径流过程进行模拟,并对模拟结果进行对比分析,依据肯斯瓦特水文站2000—2013年实测流量数据对模型进行校准,其中2000—2010年为率定期,2011—2013年为验证期,径流过程模拟如图5所示,模型模拟与实测日平均流量散点图如图6所示。

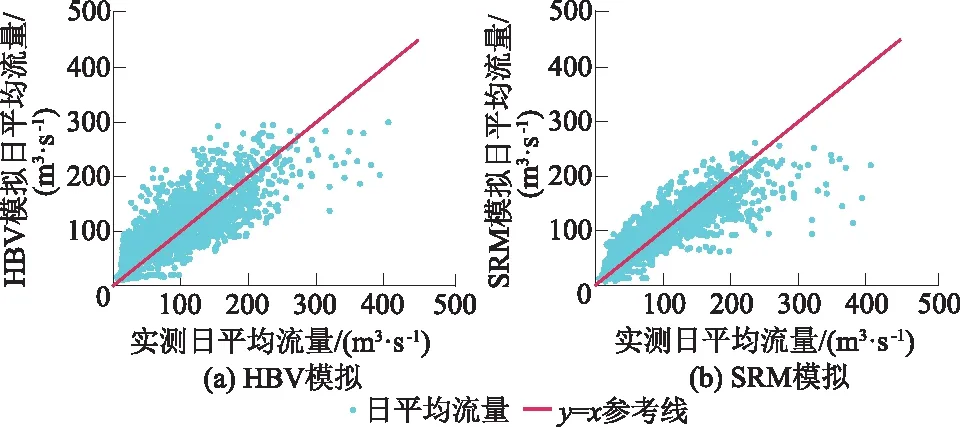
图6 模型模拟与实测日平均流量散点图

对HBV模型和SRM日尺度的径流过程模拟效果(图5(a))进行对比分析。流域每一年中最大的洪水过程均出现在夏季汛期,且往往起涨迅速,洪峰陡峭。HBV模型对于汛期洪峰的模拟效果相比SRM更好,但两个模型对洪峰流量的模拟值都普遍偏小,可能的原因是HBV模型在对气象数据进行插值时将流域分为17个子流域,而SRM仅将流域分为8个海拔区,HBV模型更能反映中高山区的垂直气候带差异和研究区降水和气温分布的空间异质性,且HBV模型包含的土壤水分模块参数包括土壤含水量比值系数(Least Potential Soil Evapotranspiration Coefficient,LP)和降雨或融雪对径流贡献参数(Soil Moisture Bands Empirical Threshold Parameters,BETA)等,能计算出前期土壤含水量和降雨或融雪在径流量的占比,从而对夏季汛期以降雨和积雪融水混合补给为主的洪峰流量模拟效果更好。由于研究区内无气象站点,且位于中高山区,地势起伏大,模型并没全面考虑研究区的地形变化,在对气象数据进行插值时仅考虑了海拔因素,忽略了其它地理要素的影响,使得降水格点数据插值时存在低估,导致2个模型对洪峰的模拟值比实测值偏低。在后续的研究中,为减小夏季汛期洪水模拟的误差,可以根据坡度、坡向等因素,对气象数据的插值进行修正。

对比分析月尺度的径流过程模拟效果(图5(b))表明,玛纳斯河径流年内分配很不均衡,流量从每年5月份开始迅速增长,至7、8月份达到峰值,从9月份开始迅速跌落,然后从10月份至次年4月份流量基本维持在较低水平。从2个模型的模拟效果来看,HBV模型基本能反映出流域实际月尺度的径流变化过程,但对于冬季至翌年春季以融雪补给为主的径流过程模拟比SRM偏高,原因可能是高山区流域地形复杂,缺少可利用的流域水文地质实测数据,进而缺乏对流域地下水在空间和时间分布状况的认识,HBV模型产流模块的下渗系数(Percolation to Lower Zone,PERC)、上层水库含水阈值(Upper Zone Water Content Limit,UZL)等参数被设置为常数,整个流域被视为相同的下渗和持水特性,导致流量的模拟值相比实测值存在偏差。

为直观表明HBV模型和SRM与实测径流在不同流量区间的模拟效果,分别作2000—2013年HBV模拟和SRM模拟与实测日平均流量散点图(图6),分析两模型在不同流量区间的模拟效果可知,SRM在10～150 m3/s流量区间,模拟与实测流量集中分布在y=x参考线的临近区域,模拟与实测流量基本一致;当实测流量较高(200 m3/s以上流量区间),模拟流量明显偏低,这与HBV模型相比效果较差,可能是由于SRM输入数据有流域每日积雪覆盖率,模型参数主要与温度相关,相比HBV模型更侧重受温度影响较大的融雪补给径流计算,而对降雨径流的计算比较简化,导致流域在7、8月份汛期融雪补给径流作用较小、降雨补给径流作用较大情况下,SRM相比HBV模型不能较好地模拟实际峰值流量。

3.3 径流模拟结果评价

根据表6两模型模拟结果和各评价指标含义,对比NSE和lg(NSE)指标可知,HBV模型相比SRM在高流量处,模拟值与实测值的一致性更好,在低流量处则较差;RSR指标反映出HBV模型的模拟值与实测值的偏差比SRM更小,整体拟合程度更高;2种模型的PBIAS都为负值,说明模拟值的平均值均比实测值偏高,SRM模拟值与实测值的平均趋势比HBV模型更加吻合。整体参照表3评价等级分类标准,以评价指标中最低的性能评价等级作为模型总体的评价等级,HBV模型和SRM的2个时间尺度径流模拟效果评价等级都为“良好”,2个模型在玛纳斯河流域的径流模拟均具有较好的适用性。

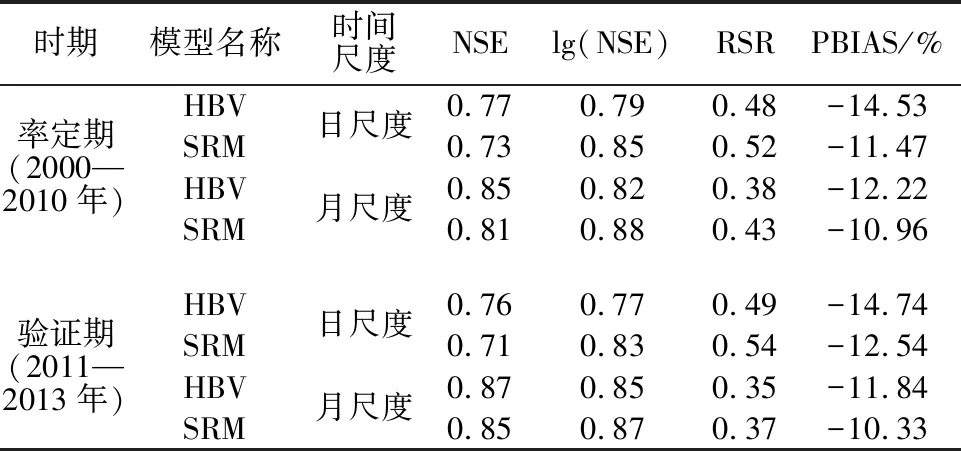
表6 2000—2013年的径流模拟结果评价指标值

4 结 论

本文通过中国地面日值降水和气温格点数据集驱动HBV模型与SRM,对比分析2个模型在资料稀缺的玛纳斯河流域融雪径流的模拟效果,研究HBV模型在新疆天山北坡山区流域的适用性,得出以下结论:

(1)利用北半球逐日无云二值积雪产品得到研究区多年月平均积雪覆盖面积变化过程,1月份积雪覆盖率最大(81.2%), 8月份最小(20.5%)。多年月平均积雪覆盖率与多年月平均流量呈负相关,决定系数R2=0.67,玛纳斯河流域积雪融水对径流的补给作用明显。

(2)基于降水和气温格点数据集经空间插值得到的研究区多年平均降水和气温的空间分布,能基本反映流域的垂直气候差异性,与相关研究结果一致,相对于研究区域内仅有的肯斯瓦特水文站实测气象数据在空间上更有代表性,对于玛纳斯河流域缺乏气象资料的高山区,数据集可作为径流模拟的输入数据。由于新疆天山地区气象站点稀疏,基于气象站点插值的降水和气温格点数据集的空间分辨率和准确性需要进一步提升。

(3)HBV模型和SRM在流域日尺度和月尺度径流过程的模拟效果评价等级均为良好,两个模型在玛纳斯河流域的径流模拟均具有较好的适用性。HBV模型相较SRM无需输入流域每日积雪覆盖率数据,其对融雪和降雨混合补给的洪峰流量模拟效果更好,整体的模拟值与实测值偏差更小。HBV模型总体相比SRM在缺乏水文气象资料的玛纳斯河流域有更好的适用性。