弹性参数变异下孔径变形法地应力测试实践

赵顺利,邓伟杰,郭 冲,杜卫长,高慧民

(1.江河安澜工程咨询有限公司,郑州 450003; 2.黄河勘测规划设计研究院有限公司,郑州 450003)

0 引 言

地应力是赋存在岩体内的天然应力,对于工程勘察、设计、施工具有重要意义[1-2]。为准确获取工程区域的应力状态,以地应力测量、计算、反演等为代表的一系列技术手段被陆续提出[3]。由于地应力赋存条件的复杂性,地应力原位测量依旧是工程中获取准确应力状态的主要手段。

目前工程实践中较为成熟的地应力原位测试方法主要包含应力解除法和水压致裂法,2种测试方法互有优劣,从三维地应力测量的准确性和可靠性上而言,应力解除法更有优势[4]。

具体到应力解除法,目前工程实践中的计算方法以岩体各向同性的假设为基础,但是各向同性的假设在弹性参数变异明显的裂隙发育地区表现出一定的局限性。对于具体的工程设计而言,岩体的弹性参数变异特征对岩体稳定性分析具有重要的意义[5],地应力测试的准确性则更为关键[6-7],亟需发展裂隙发育区弹性参数变异条件下的地应力计算模型[8]。

为了解决应力解除法地应力计算过程中的三维地应力计算问题,基于横向各向异性的理论模型得到一定的发展。如何江达等[9]根据弹性理论中的复变函数方法,推导了三维地应力计算公式;田鹤等[10]则进一步建立了横向各向异性岩体的弹性参数预测模型。但是横向各向异性的地应力计算模型尚不能满足工程需求,韩昌瑞等[11]发展了正交各向异性岩体的二维解析模型,推导了孔径变形法的孔径径向位移公式。但是目前的研究中,针对弹性参数变异的工程实践较少,尤其是对于裂隙发育导致的弹性参数变异,构建地应力计算模型时,应考虑到测试数据的筛选和弹性参数获取的难易程度,以便进一步提升应力解除法地应力测试结果的准确性和可靠性。

基于此,以应力解除法中的孔径变形法为基础,构建适用于裂隙发育区弹性参数变异条件下的三维地应力计算模型,建立测试数据的筛选原则,并通过具体的工程实践,开展了弹性参数的选取工作,结合水压致裂测试成果和地形地貌分析,验证了三维地应力计算模型的合理性。

1 裂隙发育区孔径变形法测试

1.1 孔径变形法地应力测试步骤

孔径变形法属于应力解除法的一种,是目前最好的测试方法之一,在国内外的工程实践中应用广泛[12-13]。具体测试是通过测量应力解除前后的孔径变形,结合钻孔岩芯弹性参数,计算测试区域的三维地应力张量。

区域的三维地应力通常包含6个独立参量,一般情况下需要3个不同方向的钻孔测试数据完成计算。工程实践中多采用3孔交汇的布置方式,钻孔间的夹角为45°左右,钻孔间距在满足仪器操作的情况下尽可能接近。对于裂隙发育区的孔径变形法测试,三维地应力计算所需的独立方程数量和常规方法一致,因此在准确确定弹性参数的情况下,钻孔的要求可按照上述要求执行,也可适当增加钻孔数量和测试段数量。

具体到单一钻孔,测试主要步骤如图1所示。通过大口径钻头钻进至预定位置,通过孔底磨平及钻导向孔后,经小口径钻头钻进测试孔,保证大小孔同轴。安装孔径变形计并将导线引出后,通过大口径钻头逐级钻进,记录不同钻进深度处的应力解除造成的孔径变形,待孔径变形读数稳定后或钻进至一定深度后,停止读数及钻进[4]。

图1 孔径变形法地应力测试步骤

此次孔径变形计采用的是36-2型变形计,内部结构如图2所示。孔径变形计共分布有4对触头,相邻触头夹角为45°,单次测量最多可获得4个有效测量数据。

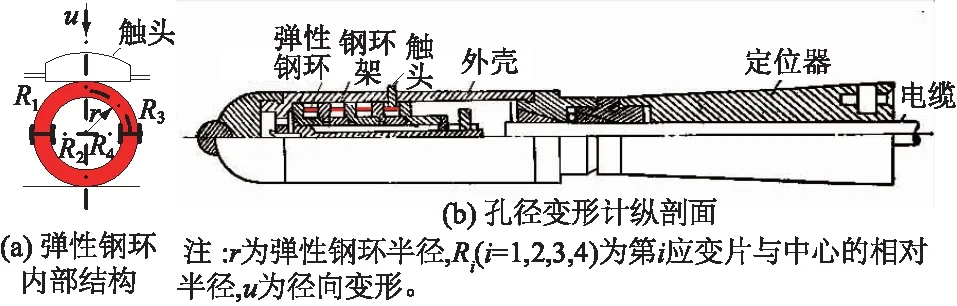
图2 孔径变形计结构

1.2 弹性参数变异条件下的三维地应力计算

各向同性的假设下,孔径变形法地应力测试中的孔径变形与三维地应力的关系可用式(1)表示。

E(uij/d)=Ak1σx+Ak2σy+Ak3σz+Ak4τxy+

Ak5τyz+Ak6τzx。

(1)

式中:E为测试区域钻孔岩芯弹性模量;uij为变形计第i个钻孔第j对触头测的孔径变形;d为测试孔孔径;Ak1、Ak2、…、Ak6为方程应力系数,k=4(i-1)+j(j=1～4);σx、σy、σz、τxy、τyz、τzx为大地坐标系O-xyz下的应力分量,其中z轴铅锤向上为正,x轴正北向为正,y轴方向由右手系确定。

对于裂隙发育区,各向同性的假设通常无法满足,对于不同测试段而言,其弹性参数通常也不一致。具体实践中,测得每个测试段的弹性参数通常较为困难,且会增加计算的复杂度,因此取每个钻孔中岩芯的弹性参数一致,不同钻孔间的弹性模量不一致,在能满足弹性参数变异假设的前提下,保证应力计算的简便性。

对于第i个钻孔而言,应力解除过程中,考虑到岩芯与钻孔轴线平行方向可以自由变形,计算模型采用平面应力假定,孔径变形与钻孔坐标系O-xiyizi下的地应力参量σxi、σyi、σzi、τxiyi的关系如式(2)所示。

cos2θj(σxi-σyi+2tan2θjτxiyi) 。

(2)

式中:Ei为测试区域第i个钻孔岩芯弹性模量;μi为测试区域第i个钻孔岩芯泊松比;θj为钻孔坐标系下,第j对触头与xi正向夹角。钻孔坐标系中zi轴与钻孔轴向平行,指向孔口为正;xi轴水平向;yi轴按右手系确定,上半空间为正,具体如图3所示。

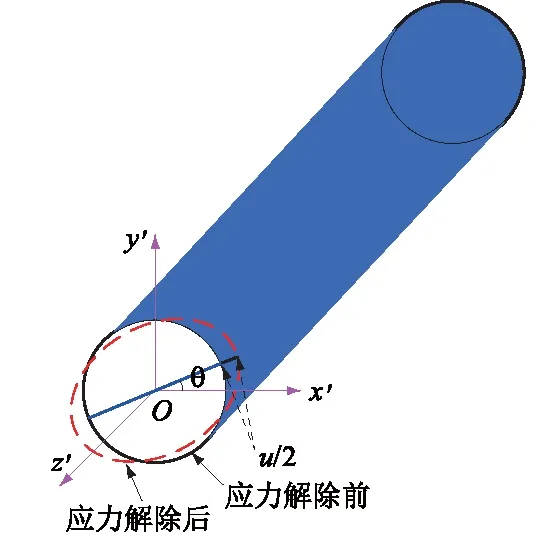
图3 钻孔坐标系

对比式(1)和式(2),孔径变形的表达式主要区别在于应力坐标的差异。其中大地坐标系和钻孔坐标系的相互联系如图4所示。图4中αi为钻孔倾角,仰角为正;βi为钻孔水平面投影方位角。根据上述参数可求得2个坐标系的各轴的方向余弦。结合三维地应力的转轴公式,将钻孔坐标系下的应力参量用大地坐标系下应力参量表示,代入式(2)中,可求得式(1)中的应力方程系数Ak1、Ak2、…、Ak6。

图4 钻孔坐标系与大地坐标系

单一钻孔中的独立方程最多为3个,为求解三维地应力,三孔交汇钻孔至少需要9个方程,由于应力的关联性,联立方程的秩为6,满足6个独立应力分量的求解条件。在弹性参数变异的条件下,第i个钻孔的弹性模量为Ei,测试孔径均为d,将式(1)、式(2)改写为矩阵形式如式(3)所示。

[EiU]/d=[A][σ] 。

(3)

式中[U]、[A]、[σ]分别为孔径变形、应力系数和应力张量矩阵。式(3)的详细展开式如式(4)所示。

(4)

为保证三维地应力的计算精度,单一钻孔的测试数据通常>3组,式(4)中获得的方程组数均>6。因此需要通过矩阵最小二乘法原理,求解三维地应力的张量的最优解,矩阵最小二乘法方程如式(5)所示。

(5)

1.3 裂隙发育区的测试数据筛选

裂隙发育区的孔径变形法测试过程中,受裂隙和结构面的影响,钻孔中孔径变形计触头的测试数据并非完全适用,直接按照推导的弹性参数变异条件下三维地应力计算公式进行计算时,则容易出现较大偏差。

因此在进行计算之前,必须进行测试数据的筛选。结合工程实践经验,总结了如下3个测试数据的筛选原则。

(1)结合取出的岩芯段,分析裂隙发育和结构面贯穿情况。由于孔径变形法基于平面应力假设,因此一对触头间的岩体未出现明显的裂隙或结构面,则对应触头的数据可以保留。由图2所示,触头的直径一般情况下均<5 mm,因此触头确定的平面为一窄平面,对裂隙发育区局部完整岩块具有较高的适用性。

(2)检查解除过程中测试数据是否满足或接近解除深度h与释放应变ε典型曲线形式。h-ε典型曲线可划分为4个阶段,根据不同阶段的孔径大小特征,典型的曲线类型如图5所示。相关研究表明,对于高应力区,应力解除过程中,岩芯未发生明显破坏时,其h-ε典型曲线依旧满足图5的规律[14],但是由于高应力区的复杂性,解除岩块出现较大塑性变形时,孔径变形法将不再适用。测试曲线与典型曲线形式差距较大的数据应舍去。

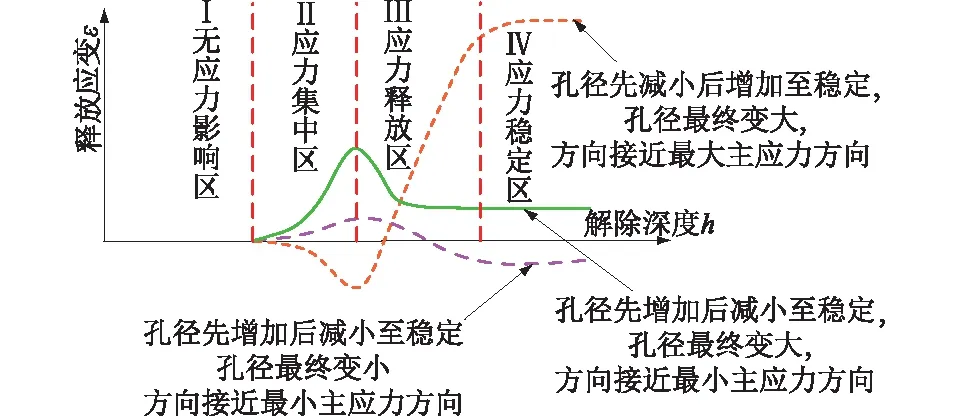
图5 解除深度与释放应变的典型关系曲线

(3)前2个原则初步筛选后,将剩余的钢环结果进行拟合处理。对于同一个钻孔中的所有测试数据,式(2)可以改写成式(6)的形式,即在同一钻孔中的钢环变形与2倍的钢环角度呈正余弦关系,设置对应正余弦函数表达式,通过计算机进行最小二乘法拟合处理,将离散的点进行剔除。

uij=a+bcos(2θj+c) 。

(6)

式中a、b、c为待定系数。

2 工程应用

结合裂隙发育区的弹性参数变异特点,在理论推导和工程实践的基础上,建立了弹性参数变异条件下孔径变形法三维地应力计算模型和测试数据的筛选原则,为进一步验证方法的有效性,结合实际的工程实例进行验证。

2.1 工程概况

工程实例为九峰山抽水蓄能电站工程,工程位于河南省辉县市,站址区位于太行山区,属于中低山地貌类型,区内岸坡陡峻,局部近直立,河谷断面大致呈“U”型;坝址区出露地层岩性为第四系覆盖层和寒武系灰岩、页岩中元古界汝阳群砂岩及太古界片麻岩,库坝区两岸基岩基本裸露,第四系覆盖层主要分布于山坡和沟谷内,上库右岸及下库河床覆盖层较厚,其他位置零星分布。

根据工程勘察需求,下库区域的地下厂房PD06探洞内开展了1组孔径变形法的地应力测试工作。下库库区出露基岩为太古界片麻岩和中元古界巨厚层石英砂岩,岩体为整体块状结构,岩体强度较高。片麻岩局部发育云母富集形成的软弱夹层,库区发育多条断层,局部节理裂隙发育,地质构造以北东向为主。

具体的孔径变形法测试位置及断面情况如图6所示。测试位置位于地下厂房洞中,岩性为太古界片麻岩,质地坚硬,发育一定量的岩脉,节理和结构面发育,出现明显的弹性参数变异现象,因此基于各向同性假设的试验方法不再适用。

图6 孔径变形法地应力测试断面

按照3个测试数据的筛选原则确定的试验数据如表1所示,绘制钢环变形与2倍钢环角度关系曲线,并用正余弦函数进行拟合,具体如图7所示。通过图7可以发现,筛选的测试数据基本上位于拟合函数上下,数据可以进行三维地应力的计算。

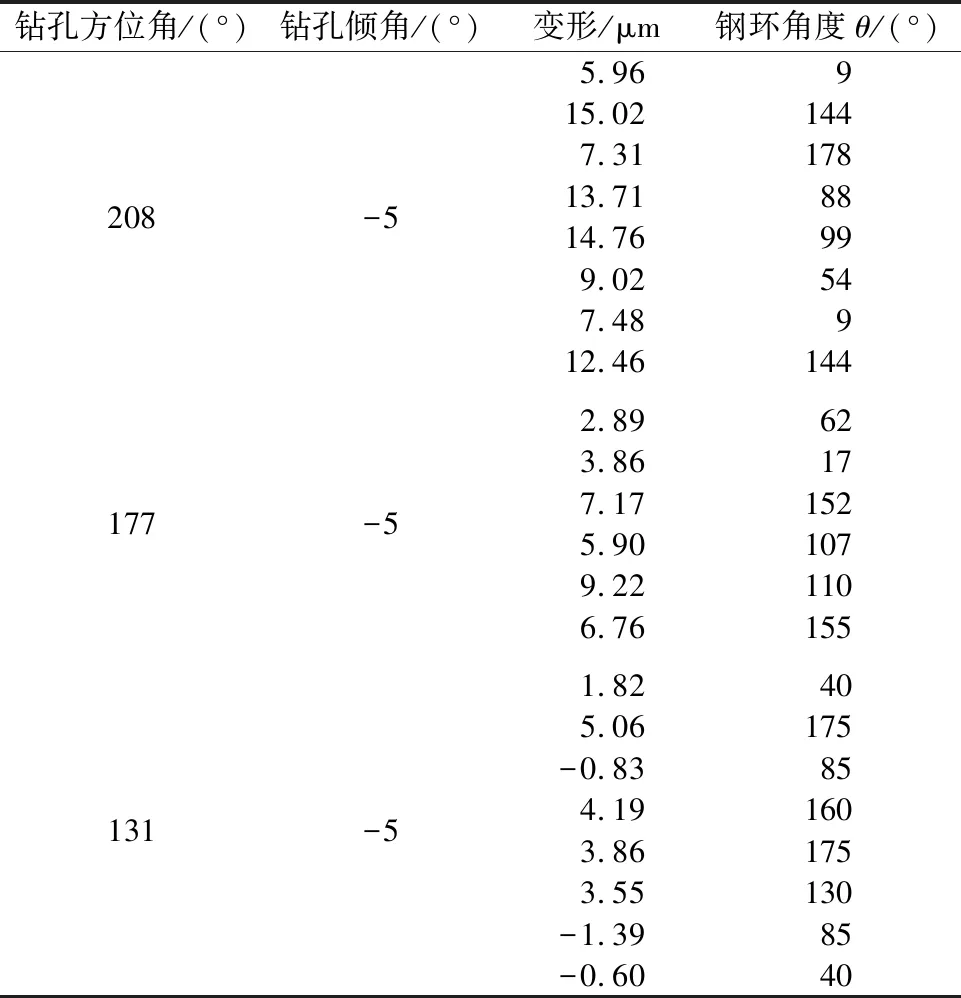
表1 三维地应力计算数据

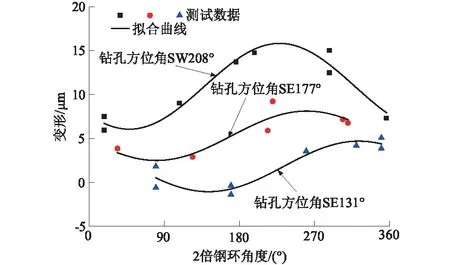
图7 钢环变形与2倍钢环角度关系曲线

2.2 弹性参数选取

由式(5)可知,为了正确地计算三维地应力状态,需进行弹性参数选取。不同于考虑库区岩体宏观尺度的地应力计算,应力解除法的钻孔岩芯尺寸为岩块,变形和应力的关系均是岩块尺度,因此在孔径变形法的分析中,通常做法是采用岩块参数[4]。

为了更准确地获得弹性参数指标,通过围压器进行弹性模量测试,围压器的结构原理如图8所示,即通过取出的带有孔径变形计的完整岩芯放入围压器中,经橡皮囊均匀地在测试岩芯四周施加一定围压,测读压力和孔径变形计的读数,因为应力解除过程是卸压的过程,采用围压卸载过程的应力变形关系进行弹性模量的计算。此次围压施加最高为10 MPa。由于孔径变形法只能测试径向变形,此次的泊松比μ测试通过室内的单轴压缩变形获得。具体的弹性参数如表2所示。由表2的测试结果可以发现,此次测试的岩芯弹性参数变异较为明显。

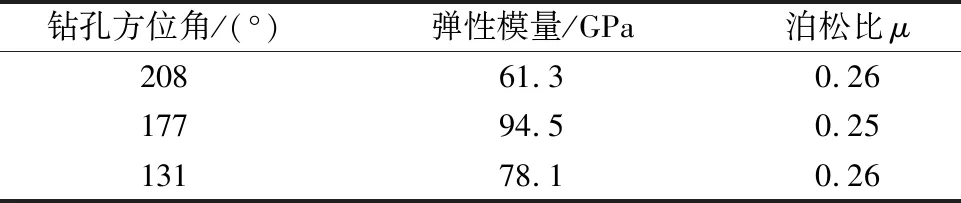
表2 弹性参数

图8 围压器的结构原理

2.3 试验成果分析

根据表1、表2的测试数据,通过MATLAB软件按照式(5)进行编程计算,最终计算的测试断面的三维地应力状态如表3所示。

表3 三维地应力计算

为进一步验证弹性参数变异条件下的三维地应力计算模型的合理性,结合测试断面附近的区域应力场特征、水压致裂测试成果和地形地貌特征进行进一步的分析。

大量的现场试验结果表明,我国地应力场的最大水平主应力方向有较明显的分区特征[15]。研究区隶属于东北—华北应力区,基于震源机制解的统计结果表明,东北—华北应力区最大水平主应力方位的分布比较集中,主要是近EW向和NEE向,表明该应力区构造应力场在水平方向上的主要特征是近EW—NEE向的挤压。工程区的最大主应力方向近EW向,与区域的应力特征相符。

PD06探洞在XCFZK01、XCFZK02和XCFZK03钻孔开展了水压致裂地应力测试工作,钻孔位置如图6所示。水压致裂测得最大水平主应力方向为N64°E—N77°E附近,最大水平主应力σ1、最小水平主应力σ2与测试深度H的拟合曲线表达式如式(7)所示。

(7)

式(7)表明,在测试范围内,最大水平主应力和最小水平主应力随测试深度呈现略微增大的趋势。

水压致裂地应力测试得到的应力数据反映的是钻孔横截面上的平面应力状态,并非是三维地应力,因此为了进行对比,将表3中的三维地应力在水平面上进行投影,投影后的结果与水压致裂测试成果对比,如表4所示。

表4 孔径变形法与水压致裂测试成果对比

从表4可知,孔径变形法测得三维地应力在水平方向上的投影得到的最大水平主应力基本上与水压致裂测试结果一致。水压致裂法地应力测试中,如果与钻孔轴向相同的方向上应力为主应力之一,则水压致裂测试得到的平面最大主应力方向基本可以反映工程区域的最大挤压方向,反之,水压致裂地应力测试在反映应力空间状态时则具有较大的局限性。

从量值水平而言,孔径变形法测试得到的量值略低于水压致裂测试成果。在裂隙发育区,由于原生裂隙和结构面的存在,水压致裂得到的压裂缝可能会偏离截面最大主应力方向,得到的测试数据存在偏大的可能,但是对于工程而言,是偏安全的。综合考虑裂隙发育区的弹性参数变异特征和数据综合筛选原则,此次孔径变形法基本上避免了原生裂隙和结构面对测试数据的不良影响,测试成果相对可靠。2种方法在原理上的差异,导致应力出现略微差异,但是对工程而言,都是可靠的。

地应力测试断面在整个工程纵剖面上的位置如图9所示,将最大主应力绘制到图9中,可以发现,最大主应力挤压方向与地形地貌特征也较为吻合。

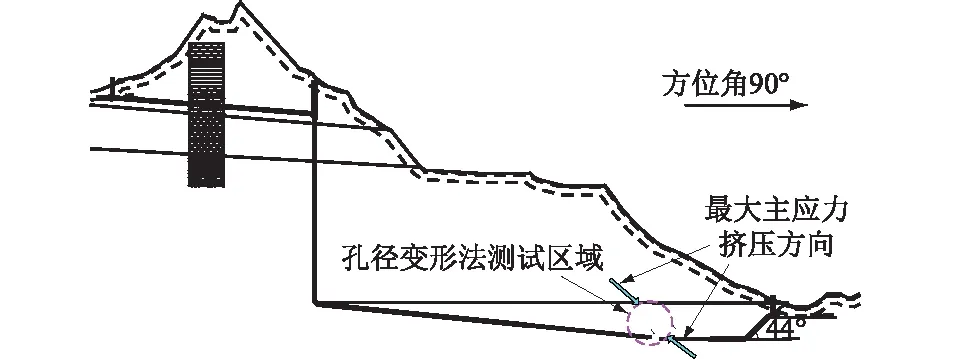
图9 工程纵剖面

通过弹性参数变异条件下的三维地应力计算模型得出的应力结果与区域应力场特征、水压致裂测试成果、地形地貌特征的综合对比可以发现,不同的结果可以相互印证,进一步表明了弹性参数变异条件下的三维地应力计算模型的合理性。

3 弹性参数对应力结果的影响

3.1 泊松比对应力结果的影响

从三维地应力计算公式可以看出,三维地应力计算精度依赖于弹性参数的选取。

具体到泊松比时,Hakala等[16]进行孔壁应变法地应力测试工程实践研究,结果表明泊松比对计算结果为中等影响,对应力量值方面的影响约有20%～60%,对应力方向则几乎无影响。值得注意的是,Hakala等[16]的研究存在一定的夸大,其泊松比的取值范围为0.1～0.35,实际测试中,一定量的试验不会导致泊松比大比例的偏差。对于孔壁应变法而言,泊松比在三维地应力计算公式中一般为1次幂,孔径变形法中泊松比多为2次幂。为进一步研究孔径变形法的影响,通过地下厂房测试区域的地应力测试数据,以表2中泊松比为基准,取±50%的偏差(方位角208°和131°的钻孔泊松比范围为0.13～0.39;方位角177°的钻孔泊松比范围为0.125～0.375),分别计算泊松比对主应力量值、方位、倾角的影响。

主应力量值的偏差如图10所示,泊松比的偏差对主应力量值影响较小,在泊松比50%的偏差下,最大主应力量值偏差≤10%,远小于Hakala等[16]的研究结论。

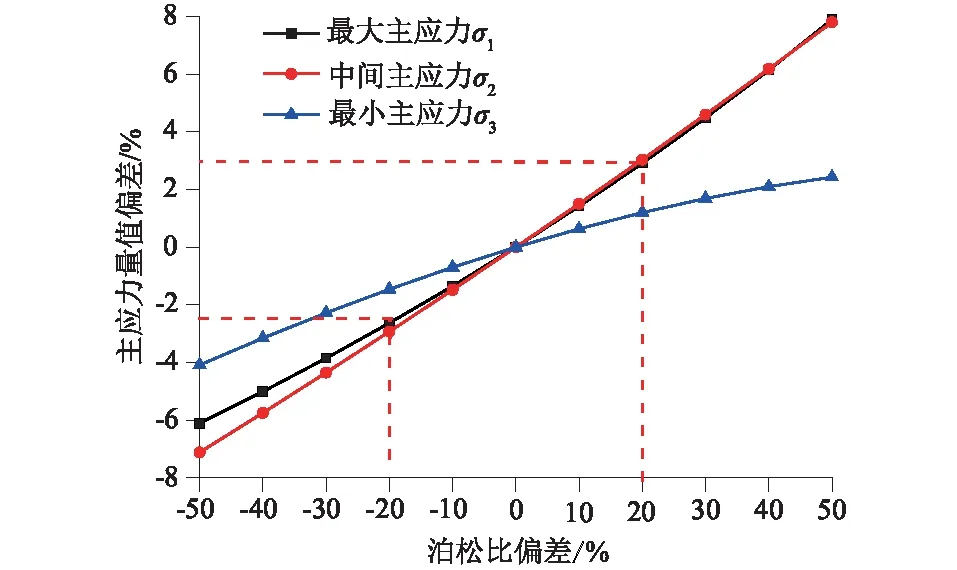
图10 泊松比对主应力量值的影响

为使三维地应力方位、倾角可视化,采用下极点的全空间赤平投影技术,原理如图11所示[17]。可视化后的主应力方位、倾角如图12所示。由图12可知,泊松比对最小主应力的方位影响最大,相差约5°左右,对中间主应力的方位影响最小,相差约3°;泊松比对中间主应力的倾角影响最大,相差约5°,对最大主应力的倾角影响最小,相差约1°。

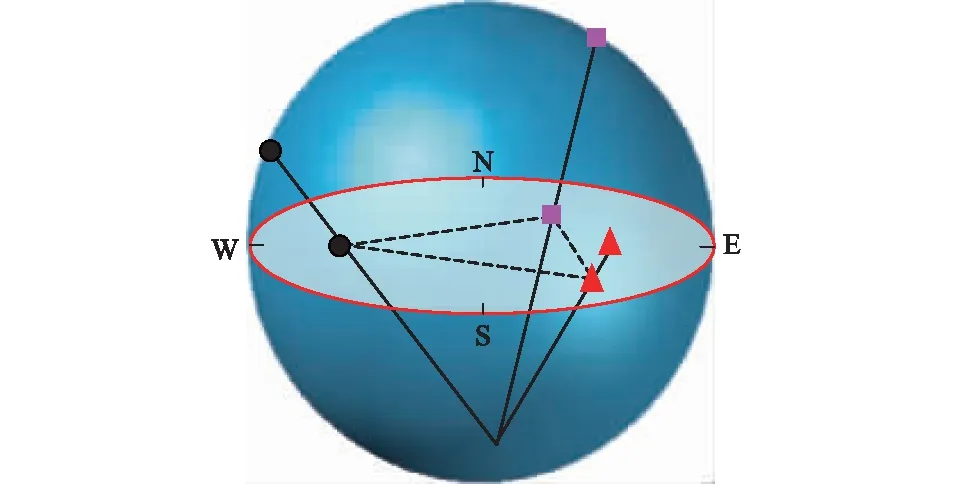
图11 下极点全空间赤平投影技术原理

图12 泊松比对主应力方位、倾角的影响

实际情况中,泊松比的试验偏差通常不会太大,结合理论计算,泊松比对主应力的计算结果影响较小。

3.2 弹性模量对应力结果的影响

对于各向同性的岩体而言,由式(5)可以发现,弹性模量E对三维地应力计算结果量值呈正比例影响,对应力方向、倾角无影响。

此次测试中可以明显发现,弹性模量的弹性参数变异明显,为进一步研究弹性模量对应力结果的影响,通过地下厂房测试区域的地应力测试数据,以表2中弹性模量为基准,方位角131°钻孔的弹性模量78.1 GPa为各向同性条件下的弹性模量,其他2个钻孔弹性模量向各向同性状态下偏离时为正向偏离,通过式(8)定义偏离度PL。

(8)

式中:Eh为偏离后弹性模量;E0为初始弹性模量;Ea为各向同性条件下的弹性模量。

使方位角208°和177°的钻孔岩芯弹性模量按照一样的偏离度向各向同性方向正偏离,偏离度PL分别取20%、40%、60%、80%和100%。分别计算弹性模量对主应力量值、方位、倾角的影响。

主应力量值的偏差如图13所示,弹性模量的偏差对主应力量值影响较大,在实际的弹性参数变异弹性模量状态向各向同性状态过渡时,中间主应力的偏差最大,达到40%左右;最小主应力的偏差最小,最大值不超过3%。

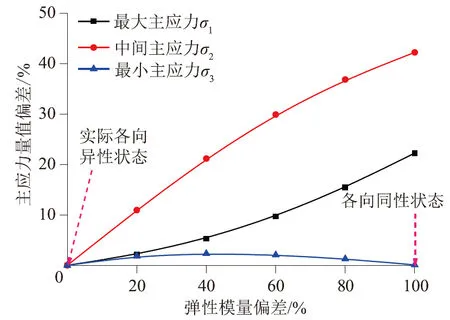
图13 弹性模量对主应力量值的影响

基于赤平投影技术可视化后的主应力方位、倾角如图14所示。由图14可知,弹性模量偏差对最大主应力的方位影响最大,相差约40°,对中间主应力的方位影响最小,相差约20°;弹性模量偏差对中间主应力的倾角影响最大,相差约20°,对最小主应力的倾角影响最小,相差约5°。

图14 弹性模量对主应力方位、倾角的影响

通过上述研究可发现,对于弹性参数变异明显的地区,如果不考虑弹性模量的弹性参数变异,则孔径变形法地应力测试的计算结果会出现较大偏差。在裂隙发育地区,通过工程实践表明,提出的弹性参数变异条件下三维地应力计算模型可达到较好的效果。

但是针对弹性参数的分析过程可以发现,提出的计算模型均是建立在线弹性的基础上的,事实上,高应力区或者强卸荷区,通常存在塑性变形或者孔壁破坏,此时基于线弹性的理论和方法将不再适用。

4 结 论

结合裂隙发育区的孔径变形法测试特点,构建了弹性参数变异条件下的孔径变形法三维地应力计算模型,并提出了测试数据的筛选原则,通过具体的工程实践,验证了计算模型的合理性。通过研究得到如下结论:

(1)具体的工程应用表明,裂隙发育区弹性参数变异条件下孔径变形法三维地应力计算模型的分析结果和水压致裂测试方法、地形地貌特征得出的结论较为一致。

(2) 孔径变形法和水压致裂法存在原理上的差异,表现在应力量值方面存在一定的偏差,对于工程而言,2种方法都是可靠的。水压致裂法主要测定平面应力,在三维地应力计算方面,应力解除法更有优势。

(3) 结合工程实践经验和平面应力假设,总结的3个测试数据的筛选原则可以一定程度上剔除离散的应力数据,具有较强的工程实用价值。

(4)对于孔径变形法而言,泊松比的偏离对三维地应力的计算结果影响较小,弹性模量的偏离则会明显影响地应力的量值、方位和倾角,在具体的弹性参数选取时,应重点关注弹性模量的准确性。