RCA（1）时间序列模型均值变点的在线监测

贾伟亚，魏岳嵩，徐建中

（1.亳州学院 教育系，安徽 亳州 236800；2.淮北师范大学 数学科学学院，安徽 淮北 235000；3.亳州学院 电子与信息工程系，安徽 亳州 236800）

0 引言

变点问题起源于质量控制领域，由于生产线中产出的产品总存在不合格产品，为保证产品质量，需将不合格产品及时抽出，不合格品出现的时刻就是变化点，这便产生对变点的研究。随着变点问题研究的深入，其研究方法和分析模型也相应多样化，从而被广泛应用到金融、工业、医学和水文等领域。如谭长春等［1］应用变点检测分析金融传染问题；周佳琪等［2］利用变点模型分析房地产价格的影响因素；尚云艳等［3］和仲建兰等［4］应用变点模型研究控制图的问题；张羽等［5］和张清杰等［6］在研究水文问题中应用变点分析法。

变点的在线监测问题是指在已有模型基础上对新观察数据进行在线监测，直到出现变点才停止［7］。许天明等［8］研究AR（p）（p阶自回归）模型中存在一个均值变点的估计问题；胡尧等［9］研究方差非参数回归模型中均值与方差双重变点的估计；朱慧敏等［10］研究方差变点模型CUSUM（Cumulative Sum）型估计量的相合性；胡丹青等［11］研究线性回归模型多结构变点检测方法；李美琪等［12］研究线性回归模型中相依数据的多结构变点问题。Gombay等［13］引入有效得分向量，将变点的在线监测问题推广到AR（p）（p阶自回归）模型中。薛义新等［14］对自回归模型参数变点进行分析，构造残差累积和监测统计量，给出监测统计量的极限性。齐培艳等［15］研究多项式回归模型中系数变点的在线监测问题。Na等［16］讨论变系数和变方差的在线监测问题。Qin等［17］研究线性过程方差变点估计强相合性。Aue等［18］对RCA（1）时间序列模型均值变点的监测统计量进行分析研究，得到统计量的极限分布性质。Li等［19］引入波动监测程序对RCA（p）模型中参数变点进行在线监测分析研究。窗宽参数在高频数据波动率和短期负荷区间预测等分析中均有应用［20-21］。在变点问题的研究中，刘维奇等［22］对多元时间序列均值向量变点进行研究，引入窗宽参数构造残差累积和统计量对均值变点进行在线监测。陈占寿等［23］和李佛晓等［24］通过引入窗宽参数分别对线性回归模型和自回归模型的参数变点进行修正后的在线监测。在变点的在线监测过程中，窗宽参数对变点监测运行时间有着重要的影响，故可通过引入窗宽参数来调整运行时间。

本文对RCA时间序列模型的均值变点进行研究，在模型中引入窗宽参数，并插入窗宽参数的一致估计，用来调整监测的起始时刻，以此来提高变点分析检验势，缩短监测平均运行时间，给出一种改进变点监测方法。给出监测统计量在原假设和备择假设下的极限分布以及其后验检验，并对极限分布和后验检验进行证明，得出极限分布的一致性，以及后验检验提高检验准确率的有效性。数据模拟结果表明，可根据变点出现时刻与监测起始时刻的远近选取适当的窗宽参数，以缩短平均运行长度，达到更有效检验效果，并通过后验检验对历史样本数据稳定性进行分析，提高模型检验准确性。

1 模型假设

设随机变量{Xn} 是一阶随机系数自回归时间序列模型，满足下列等式

这里Z 表示任意正整数，φ是待估系数，{bn} 和{en} 分别是白噪声序列，且满足如下条件

这里条件（i）保证{Xn} 的严平稳性，条件（ii）是{Xn} 二阶平稳性充要条件。考虑随机变量的均值模型

这里{ }Xn是RCA（1）时间序列模型。假设历史数据前m个观测样本是没有变化的，检验如下假设H0:Δm=0，H1:Δm≠0。当 |Q(m,k,h) |第一次超过g(m,k,h)时，拒绝H0并停止。因此，定义如下停止时刻

这里infϕ=∞，Q(m,k,h)，g(m,k,h)分别表示累积和监测统计量和边界函数，定义为

引理1（RCA（1）时间序列的强不变性） 令{ }Xn是满足式（1）中条件（i）和（ii）的RCA（1）时间序列，则存在k ＞2，使得。然后，存在一个维纳过程{W(t)}t≥0，使得

这里t→∞，v ＞2，St=X1+X2+…+Xt，且令

证明 类似文献［16］中5.1对定理2.1的证明方法可证得。

由于上述统计量中的参数σs未知，便需引入另一个合适估测参数来代替方差参数σ2s，为此通过RCA（1）时间序列模型参数一致估计引入参数估计，其中m∈N。

引理2 随机变量{Xn} 是满足式（1）中条件（i）和（ii）的RCA（1）时间序列，对任意m∈N，令和分别是参数φ，σ2和ω2的弱一致估计，有

其中m→∞，→P表示依概率收敛，是的弱一致估计。

证明 结合引理1，由可测映射定理和弱一致收敛原理可证。

2 极限分布定理

定理1 令{Xn} 是满足式（1）中条件（i）和（ii）的RCA（1）时间序列，则存在k ＞2，使得＜∞和E|φ+b1|k ＜1，则存在一个维纳过程{Wˉ(t)}t∈[0,1]，使得在假设H0下有

证明 由引理1和引理2，对任意k∈N 和，当m→∞时，有

和

又因为

其中m→∞，证明得

其中m→∞。令，其中维纳分布和m是独立的，得

其中=D表示等号两边函数分布相同。{W(t)} 和{W(t)} 是2个相互独立的维纳过程，由

和

其中0 ≤t＜∞, →D表示依分布收敛。{Wˉ(t)}是一个维纳过程，可得

结论得证。

证明 由文献［15］中定理2，类似得证。

3 后验检验

令Y1,Y2,…,Ym是随机变量观测值，考虑均值模型

这里{Xn} 是RCA（1）时间序列模型。应用基于固定数据m个观测值的监测程序代替时间序列模型体系，检测平均假设变化，假设H0:Δm=0，H1:Δm≠0，k*＜m，构造累积和检验统计量

其中m→∞，σ̑S,m定义在式（8）中。

证明 由引理1和引理2，存在一个维纳过程{W(t)} ，且v ＞2 时，有

其中k→∞。因此

其中m→∞，则

其中m→∞。最后，由模型变换可得，其中{B(t)}t∈[0,1]表示布朗桥，类似①的证明，可得②也成立。

定理4 令{Xn} 表示满足式（1）中的条件（i）和（ii）的RCA（1）时间序列，存在k ＞2，使得E|e1|k ＜∞和E|φ+b1|k ＜1，有

证明 令k̑=m+k*，其中k*表示变点发生的时刻，由式（22）的累积和统计量的假设

4 模拟计算

4.1 模型检验模拟

应用python软件对模型进行数据模拟检验，主要通过检测统计量经验水平、检验的势和平均运行长度来说明模型优越性。表1是用5 000个服从标准正态分布的历史样本和10 000个检测样本经过10 000次循环得到的部分临界值表cα(γ)。基于边界函数

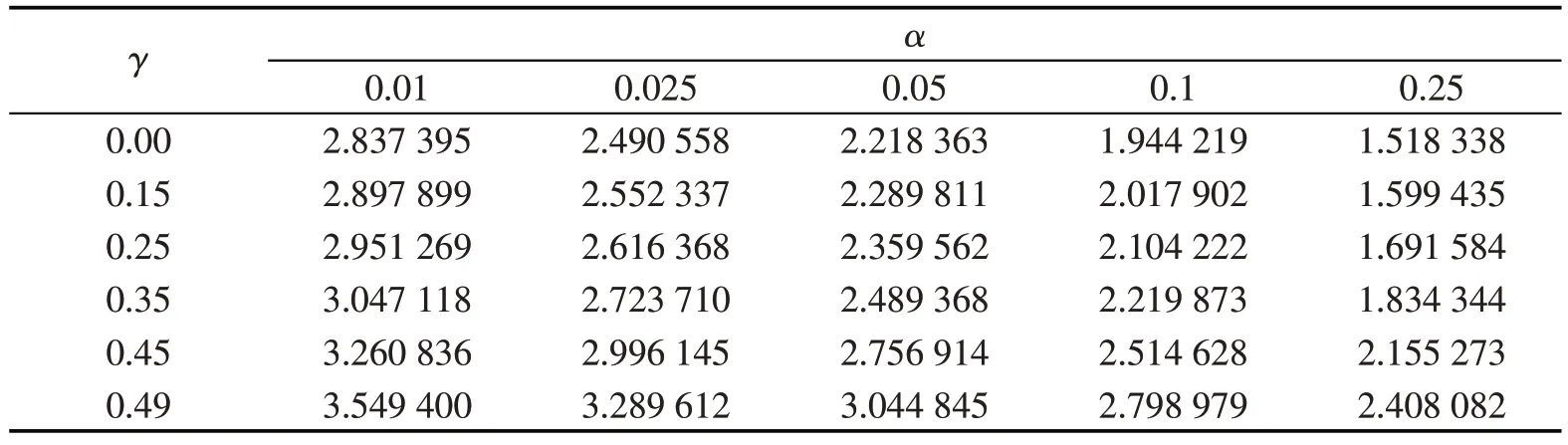
表1 不同的检验水平α 和γ 的临界值

令参数γ=0.00、0.15、0.25、0.35、0.45、0.49，显著性水平α=0.01、0.025、0.05、0.1、0.25，可以由公式得到对于不同的检验水平α和γ的临界值，如表1所示。

表2是由定理1经过2 500次模拟得到的经验水平。采用数据生成模型Xn=(φ+bn)Xn-1+en（n∈Z），其中φ=0,w2=0.5,σ2=0.5。取历史样本量m=200、500，并且令窗宽参数h=0.0、0.1、0.2、0.3、0.4、0.5，边界函数中参数γ=0.00、0.25、0.45，检验水平α=0.05，检测样本量q=m,q=2m,q=4m。由表2可以看出，当历史样本量m和窗宽h不变时，检测样本量q和参数γ在逐渐增大的时候检验势也在逐渐增大，即误报率在逐渐增大。当历史样本数据m在逐渐增大时，保持其他3个变量相同时的经验水平值基本呈现减少趋势。当γ=0.25，m=200，q=m，h=0.4；γ=0.25，m=500，q=2m，h=0.5 和γ=0.45，m=500，q=4m，h=0 时，统计量的模拟值和显著性水平更接近，但是在其他给定参数下，两者有一定的偏差。

表2 经验水平

表3和表4分别是检验势和平均运行长度。在数据生成模型中取k=0.1q和k=0.5q时加入变点，将均值在k处由0变到1，测试监测统计量，得到检验势和平均运行长度。取历史样本量m=200，监测样本量q=m，窗宽参数h=0.0、0.1、0.2、0.3、0.4、0.5，边界函数中的参数γ=0.00、0.25、0.45，比较参数γ和窗宽h变化时监测统计量检验势和平均运行长度变化。由表3 和表4 可以看出，当k=0.1q时，在不同γ和h取值下，检验势基本相同，但是随着h的增大，平均运行长度有所减小。当k=0.5q时，随着h的增大，检验势逐渐提高，平均运行长度逐渐减小。故在进行变点分析时，选取合适参数进行检验可以有效降低误差，提高检验的准确性。与不加窗宽参数h原模型进行对比分析，加入窗宽参数后效果更显著。

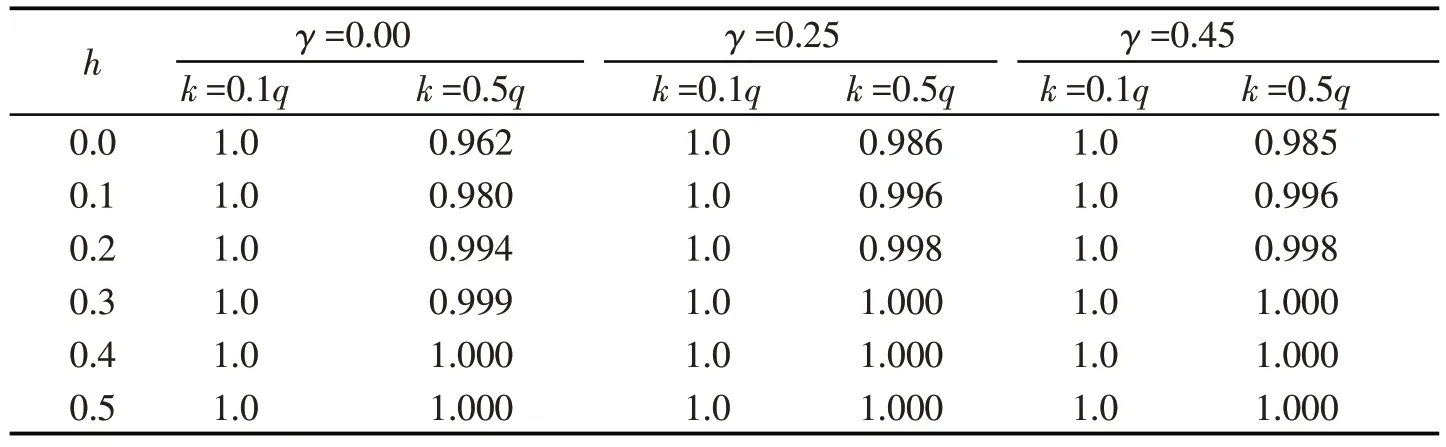
表3 检验势

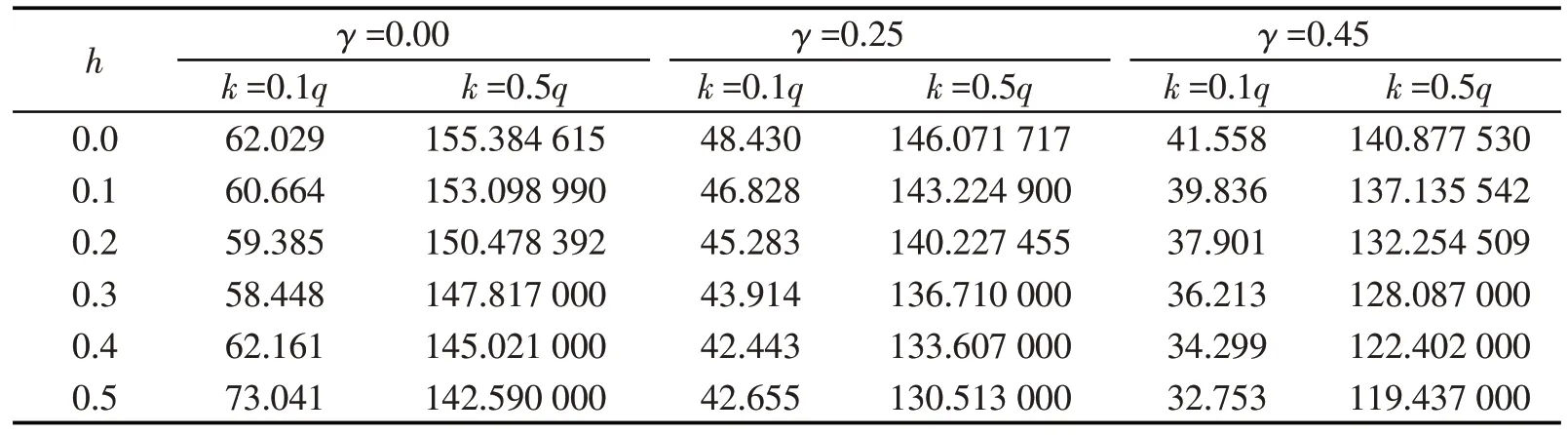
表4 平均运行长度

由表1～4综合分析可得，引进窗宽参数以后，能够调整监测起始时刻，提高检验势，缩短平均运行长度，特别是在变点出现较晚时，效果更加显著。在进行变点实际分析时，可根据变点与监测起始时刻距离选取合适γ和h。

表1～4中参数α,γ,h选取受监测样本量和历史样本量影响而会有所不同。如文献［7］所给边界函数以及参数γ取值接近于0时，监测方法过于保守，使得监测样本量相对较小时，会降低监测功效。实际变点监测问题中，监测过程迟早要结束，所以当监测样本量相对于历史样本量较小时，可取较大γ值，反之可取较小γ值，从而使经验水平接近于给定检验水平。

4.2 后验检验模拟

由于模型监测中用到历史数据，即监测中前m个数据是给定的，由上面对经验水平表、检验势和平均运行长度分析可知，历史样本量m对检测结果有重要影响，并且前m个历史数据也有存在变点可能，若存在变点则影响更大。故利用python 软件对历史样本数据进行检验，通过后验检验判别前m个历史样本是否存在变化。

表5 是基于定理3 经过1 000 次模拟得到的后验检验表。数据生成采用模型1 ≤n≤m。取历史样本量m=200、500，并且令窗宽参数h=0.0、0.1、0.2、0.3、0.4、0.5，边界函数中的参数γ=0.00、0.25、0.45。

表5 后验检验势

由表5可以看出，当历史样本量m和参数γ固定时，检验势随着窗宽参数h增大逐渐增大。当历史样本量m和窗宽参数h固定时，检验势随着参数γ的增大逐渐增大。但当窗宽参数h和参数γ固定时，检验势随着历史样本量m的增大呈现增大或者减小变化。并且当γ=0.45,m=200,h=0.3 和γ=0.45,m=500,h=0.3 时，统计量的模拟值和显著水平更为接近。综上，给定不同的参数值对分析结果有一定影响，并且本次模拟给定的前m个历史样本数据基本符合要求，可有效降低原模型检验错误率。故对于此类模型检验问题，可通过进行后验检验判断历史数据稳定性，以提高模型检验准确度。

5 结论

本文给出改进变点监测方法，用于RCA（1）时间序列模型均值变点监测。通过在模型中引入窗宽参数，用来调整监测起始时刻，以此来提高变点分析检验势，缩短监测平均运行时间。给出监测统计量在原假设和备择假设下的极限分布以及其后验检验，并对极限分布和后验检验进行证明，得出极限分布的一致性。数据模拟结果表明，可根据变点出现时刻与监测起始时刻远近选取适当窗宽参数，以缩短平均运行长度，达到更有效的检验效果，并通过后验检验对历史样本数据稳定性进行分析，以提高模型检验准确性。