双罗马控制数的界

张 宁，叶淼林，肖凤茹①

（安庆师范大学 数理学院，安徽 安庆 246133）

0 引言

近年来，随着应用数学广泛发展，控制的实际应用问题备受关注，如国际象棋问题、军事防御问题等［1-2］。控制理论作为图论研究的一个重要领域，可用来刻画图的若干性质，在不同条件下，控制衍生出的形式各有不同，如：符号控制［3］、意大利控制［4］、罗马控制［5］、双罗马控制［6］等。图的双罗马控制是图论研究领域的热点话题之一，涌现出许多丰富的结论和成果［7-10］，使控制领域逐步成为体系完整、内容充实的重要分支。

双罗马控制是在罗马控制的基础上进一步完善得到。罗马帝国的城市中，如果一个没有军团保护的城市被攻击，则该城市必须在至少一个驻扎着2个军团的城市附近，这样2个军团中一个可以被派去保卫被攻击的城市，受保卫罗马帝国的防御策略影响，在文献［2］中，Stewart最先定义和讨论罗马控制，该控制严重增加国防开支，故需要一个更有效精简的控制策略，随即引入双罗马控制。文献［6］通过改进罗马防御战略，首次给出双罗马控制数学定义，建立双罗马控制数与控制数、罗马控制数之间的关系，并根据图G的阶数，给出连通图G的双罗马控制数的上界，刻画达到这个上界的图类。文献［11］计算出路和圈的双罗马控制数的精确值，证明二部图和弦图相关的决策问题是np完备的，部分回答文献［6］中的开放问题。文献［12］给出的上下界。文献［13］确定一些特殊图的双罗马控制数，描述具有特定双罗马控制数的图。文献［14］继续讨论得出的上界和下界。文献［15］利用最小度、顶点数、周长及围长等图论参数，研究给出双罗马控制数的若干上下界。

在此基础上，本文继续研究双罗马控制数的相关性质与结论。首先考虑具有函数的图G，给出赋值为2的顶点个数满足的条件，并得到树T中叶子点和支撑点的1个赋值特点。随后引入参数：最大度、意大利控制数、最小覆盖数、打包数、3-彩虹控制数［16］，将参数的特性与双罗马控制结合，给出双罗马控制数的几个界限，拓展双罗马控制的结论，完善控制理论结构体系，丰富代数图论中对于双罗马控制研究。

1 预备知识

本文研究有限无向的简单图，设G的顶点集为V(G)，边集为E(G)，简记为G=(V,E)。G的阶 |V|和边数 |E|分别用n和m表示。对于顶点v∈V，开邻域N(v)={u∈V:uv∈E} ，闭邻域N[v]=N(v)⋃{v} 。顶点v的度degG(v)=|N(v)|，图G的最大度为Δ(G)，最小度为δ(G)，度为0的点称为孤立点。图G的分支数用w(G)表示，若G的分支数只有1个，即w(G)=1，则称图G是连通的，否则称G是不连通的。度为1的点称为叶子点，与叶子点相邻的点称为支撑点，记L(G)为G中所有叶子点构成的集合，记S(G)为G中所有支撑点构成的集合。如果V(H)⊆V(G)，E(H)⊆E(G)，则称H是G的子图，满足V(H)=V(G)的子图H称为G的生成子图。无圈的连通图称为树，若G的生成子图是树TG，则称TG为G的生成树。顶点数为n的路记作Pn，长为n的圈记作Cn。

设M⊆E(G)，对任意的e1,e2∈M，均有e1和e2不相邻，则称M为图G的匹配。若G不存在匹配M′，使得 |M′|＞|M|，则称M为G的最大匹配。最大匹配的基数称为最大匹配数，记作α(G)。设K⊆V(G)，若G的每条边都至少有1 个顶点在K中，则称K为图G的1 个覆盖。若G不存在覆盖K′，使得|K′|＜|K|，则称K为G的最小覆盖。最小覆盖的基数称为最小覆盖数，记作β(G)。设R⊆V(G)，如果对于任意不同的2个顶点x,y∈R，均有N[x] ⋂N[y] =∅，则称R是图G的1个打包集。若G不存在打包集R′，使得 |R′|＞|R|，则称R为G的最大打包集。最大打包集的基数称为打包数，记作ρ(G)。

本文主要运用几个控制函数及与之对应的控制数概念，定义如下：

定义1［3］设S⊆V是G的1个顶点子集，如果S的闭邻域满足N[S]=V，则S中的点控制G，称S为G的控制集。进一步，如果不存在G的控制集S′，使得 |S′|＜|S|，则S是图G的最小控制集，S中的顶点个数称为控制数，记作γ(G)，S称为G的γ-集。

定义2［4］设函数f:V(G)→{0 ,1,2} ，Vi={v∈V|f(v)=i} ，i=0,1,2 ，对于任意的v∈V，使得如果f(v)=0，则v必须有1个邻点在V2中，或者至少有2个邻点在V1中，则称f是V到{0 ,1,2} 的意大利控制函数或者罗马{2 }-控制函数，简记为IDFf。函数f:V(G)→{0, 1,2} 和顶点V的划分(V0,V1,V2)间存在一个一一对应关系，记作。意大利控制函数f的权表示所有顶点的赋值之和，即，如果不存在G的意大利控制函数f′，使得ω(f′)＜ω(f)，则ω(f)称为图G的意大利控制数，记作γ{R2}(G)，f称为G的γ{R2}(G)-函数。

定义3［6］设函数f:V(G)→{0 ,1,2,3} ，Vi={v∈V|f(v)=i}，i=0,1,2,3，对于任意的v∈V，使得：

（1）如果f(v)=0，则顶点v必须至少存在2个邻点在V2中，或者存在1个邻点在V3中；

（2）如果f(v)=1，则顶点v必须至少存在1个邻点在V2⋃V3中。

则f称为图G的双罗马控制函数，简记为DRDFf。f:V→{0 ,1,2,3} 和顶点V的划分(V0,V1,V2,V3)间存在一个一一对应关系，记作。双罗马控制函数的权，如果不存在G的双罗马控制函数f′，使得ω(f′)＜ω(f)，则ω(f)称为图G的双罗马控制数，记作γdR(G)，f称为G的γdR(G)-函数。

引理1［6］图G中，存在1个权为γdR(G)的双罗马控制函数f，使得赋值为1的顶点集为空集。

2 主要结果

首先给出具有γdR(G)-函数的图G中顶点集的性质，并给出树T中叶子点和支撑点的一个赋值特点。

性质1 设G是1个图，对于任意的γdR(G)-函数

证明 由定义得：V2f⋃V3f是G的1个控制集，且V2f⋂V3f=∅，则

性质2 设T是n阶树，n≥3，则：

证明 （1）Δ≤2，此时图G为路或者圈。

情况1G=Pn

恰好有1个邻点在R中，R中的每个点至少有δ个邻点在A中，因此δ|R|≤ |A|，则

定义f:V(G)→{0 ,1,2,3} ，使得

显然f是G的DRDF，所以

定理4 设G是一个连通图，阶数为n，边数为m，则对于G的生成树TG有γdR(G)≥γdR(TG)-m+n-1。

证明 如果G是一棵树，m=n-1，结论显然成立。如果G不是一棵树，设C是G中的一个圈，f是G的γdR(G)-函数，因为在C中至少有1个点赋值为0，记作v，即f(v)=0，考虑以下2种情况：

情况1 在C中，记与v相邻的其中1 点为w，且f(w)=0，此时设G′=G-vw，定义G′的DRDFg:V(G)→{0 ,1,2,3} ，g(x)=f(x)，∀x∈V。

情况2 在C中，记与v相邻的2 个点为w,z，且w,z赋值为2 或3，此时设G′=G-vz，定义G′的DRDFg:V(G)→{0 ,1,2,3} ，使得

因 此 构 造 出1 个 图G′ ，令G′ 中 包 含 圈 的 个 数 为|C(G′) |，G中 包 含 圈 的 个 数 为|C(G)|，则|C(G′) |≤|C(G)|-1，且对于情况1、情况2 均有ω(g)≤ω(f)+1，重复上述构造G′的步骤，可得到图G的一个生成树TG，使得

化简得γdR(G)≥γdR(TG)-m+n-1。

根据3-彩虹控制函数的定义，g是图G的3RDF，则

证明 设Hf的顶点划分π(Hf)={S1,S2,…,St} ，如果Hf是二部图，则 |Xf|=0，由断言1知结论成立。

假设Hf不是二部图，则t≥3。定义函数g:V(G)→2{1,2,3}，使得：

显然g是图G的3RDF，且

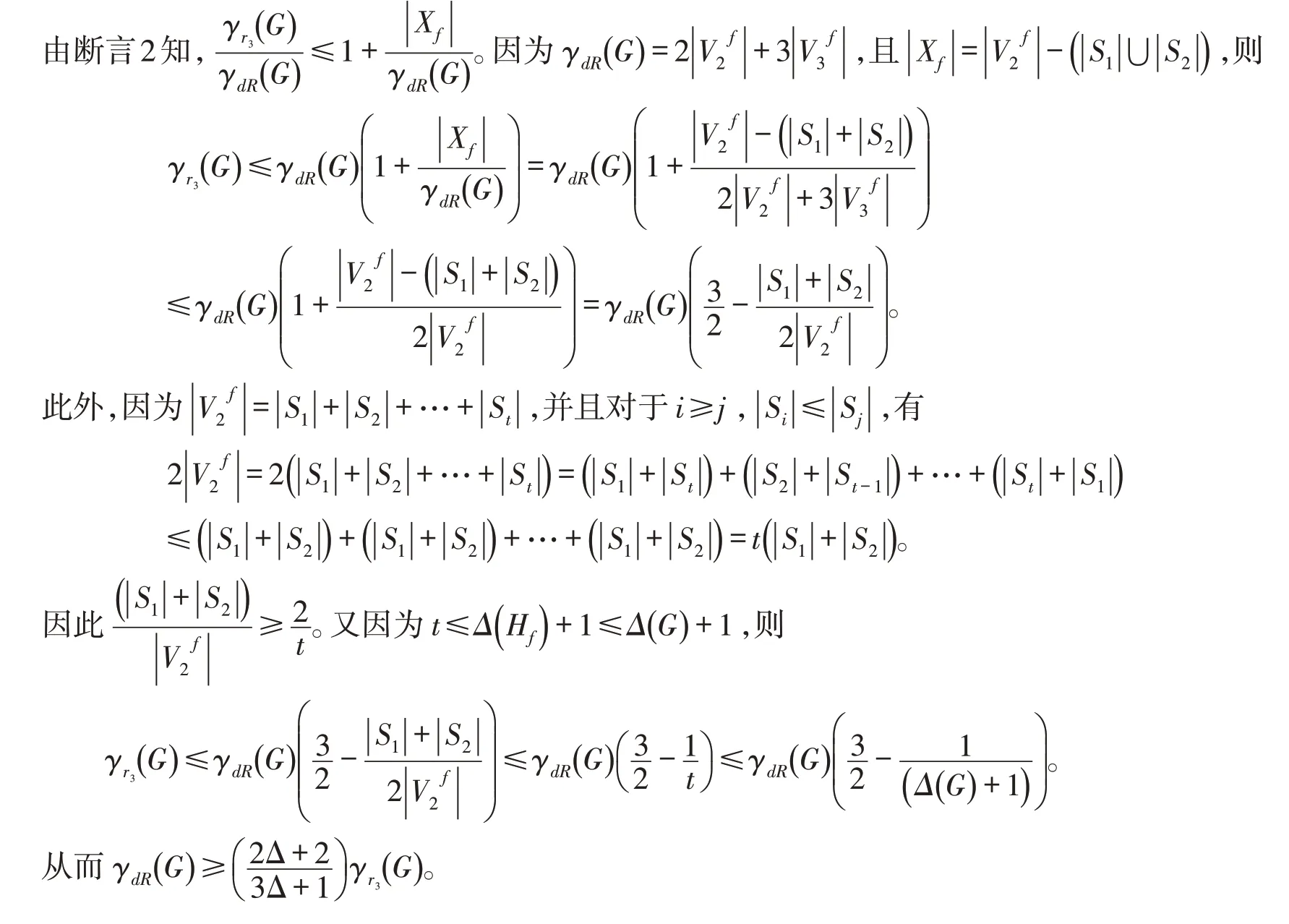
3 结语

双罗马控制在刻画图的性质方面存在重要研究意义和价值，文章依据双罗马控制数的定义，描述其与图论几个重要参数之间的关系，比较双罗马控制数与这些参数之间的大小，充实图的双罗马控制理论，如何说明这些界在什么条件达到等号成立的情况，需要继续深入探索，对研究极图方面有推广作用。