基于Q-learning的轻量化填充结构3D打印路径规划*

徐文鹏，王东晓，付林朋，张 鹏，侯守明，曾艳阳

（河南理工大学计算机科学与技术学院，河南 焦作 454000）

0 引 言

3D打印又称增材制造（additive manufacturing，AM），是一种快速成型的加工技术［1］。本文针对一种由点、线、面到体的扫描成型方式研究，3D 打印完整流程包括生成3D模型、数据格式转换、切片计算、打印路径规划、3D 打印实体5个步骤［2～4］。其中，打印路径规划是一个重要的研究工作。

简单的轻量化填充结构，如横截面图案为三角形、四边形、六边形等。这些轻量化填充结构［5］存在大量的孔洞，孔洞虽然能够节省3D 打印的制造时间和打印耗材，但也会导致打印过程中打印头出现过多的转弯和启停动作，产生空行程，影响打印时间和成型质量等问题。如何在保证顺利打印模型填充轻量化结构的前提下，通过寻找良好的路径规划达到最大程度地提升打印效率有着重要的研究意义。

目前传统的3D 打印路径规划算法主要有平行扫描［6］、轮廓扫描［7］、空间填充曲线扫描［8，9］等。在此基础上，Dreifus G等人［10］提出了一种专门用于制造晶格结构的路径规划策略，利用中国邮递员问题优化打印头在给定网格上的运动，使打印总时间最小化。Gupta P等人［11］提出一个3D打印的计算框架，用于识别打印每一层填充晶格的连续工具路径。

强化学习在许多方面［12～14］取得了较好的进展。杨德成等人［15］提出了一种基于遗传算法的智能子区域路径规划算法，先对零件切片进行分区填充，再将各个子分区的连接看作旅行商问题（travelling salesman problem，TSP）进行最优路径的求解。王祎等人［16］提出一种基于Q学习的薄壁结构3D打印路径规划方法，通过设计约束条件，寻找出打印最优路径规划方案，打印薄壁结构模型上的表现优于传统路径规划方法。但是该算法目前适用于各层切片相同的薄壁结构。

针对上述问题，本文将Q-learning 算法在薄壁模型中的应用推广到填充轻量化结构的一般模型。并经实验结果证明本文算法不仅可以用于薄壁结构的路径规划，也可以很好地应用在各层切片不同模型中。

1 基于Q-learning算法的打印路径规划

1.1 核心思想

本文方法是由2 个Q-learning算法构成。对于一个实体3D打印机喷头，当它执行转弯动作时，由一个Q-learning算法的智能体Acorner（简称Ac）表示。当它执行启停动作时，则由另一个Q-learning 算法的智能体Aup（简称Au）表示。Ac学习转弯动作策略，使打印头在转弯时，尽可能沿直线方向移动。Au则学习启停动作策略，使打印头尽可能连续地挤料。二者学习过程遵循强化学习的基本思想，待2个智能体学习结束后，Ac输出最大转弯累计奖励值的子路径，Au则将多个上述最优子路径用获取最大总奖励值的方式连接，以形成整个切片的给定条件下的最优打印路径。

1.2 预处理

对一般的空心模型内部若采用截面为三角形的轻量化结构进行填充，经分层处理后，得到切片集合。由于模型内部填充线是由多条直线段组成的，导致打印头必须在每一条填充线打印结束后抬起，再移动至下一条填充线的初始打印点开始打印下一条路径，这个过程会产生空行程，增加打印时间。

为了解决上述问题，将上述直线段进行合理连接，从而增强打印路径的连续性。将切片填充线与轮廓线的交点作为结点，填充线作为边，构成一个无向图G，这样切片的几何信息便保存在图G中。为了使打印路径的连续性最大化，并且使材料消耗最少，可在2 个相邻奇度点之间添加边。但在轮廓线凹进去的地方添加直线会破坏成型件的外观。因此，需要在轮廓线凹进去的地方沿着轮廓线添加曲线段边。连接相邻奇度点之间的边有沿轮廓线顺时针方向和逆时针方向2种构建方式，分别计算上述2 种方式所建立边的总长度，选择较小值的构建方法并执行。

1.3 寻找给定条件下的最优路径

Q-learning算法核心是构建马尔可夫决策过程（Markov decision process，MDP）数学模型，需要对智能体的三要素：状态、动作、奖励进行设定，先要对Ac的MDP 进行构建。2个智能体将切片作为环境，切片环境中的打印结点代表打印头所处的位置，故将2个智能体的状态s设定为结点。打印头转弯时在与当前位置相邻的点中选择一个待打印的点，而启停时将在整个切片中选择。因此，打印头转弯和启停动作的结果都是选择下一个打印位置，结点也可表示2个智能体的动作a。此外，将已访问结点进行标记并置于列表L中，当智能体选择一个动作抵达新状态时，可依据L是否包含此新状态，判定待执行动作是否合法，避免打印头重复打印同一路径。

在打印过程中，若打印头转弯，则会降低移动速度，并且转弯的角度越大，速度减小值就越大。因此，转弯动作的奖励Rc显然是一个与转弯角度相关的负奖励。为了让Ac尽可能多地访问图G中的结点，并使路径连续性最大化，增加一个常数π使负奖励值转化为正奖励值，同时也有效保存了奖励值区分度。打印头选择奖励值较大的动作，其转弯的角度就较小。结点间位置关系如图1，转弯动作的奖励Rc的函数表示见式（1）

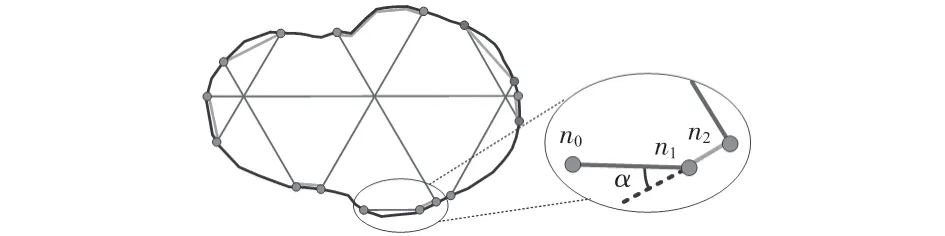
图1 结点间的位置关系

打印头当前位置为结点n1，n0是其上一个访问节点，选择下一个动作a到节点n2，其中，α 为向量n0n1与向量n1n2的夹角。

Ac的动作选择策略使用ε-greed函数，以ε的概率选择随机动作，即随机选择一个相邻的打印点；以1-ε的概率选择贪心动作，即选择奖励值最大的相邻打印点。由于ε 与Ac已学习的次数呈负相关，因此Ac学习的次数越多，打印头选择贪心动作的概率越大。构建Ac的动作价值函数Qc（s，a），其定义为Ac从当前状态仅执行贪心动作得到累计奖励的折扣值。它记录着学习过程中所有的路径策略，所以，Ac的学习过程即Qc（s，a）更新值过程，更新方式如下

式中 ¯s为新状态，¯a为¯s的贪心动作，γ为折扣因子。

由贝尔曼方程可知，Qc（s，a）迭代多次后，会收敛于一稳定函数（s，a），它便是Ac学习到的最终转弯策略，可根据定义得到一条最大累积转弯奖励值的路径Ps，并且这条路径一定是连续的。

接下来是对Au的MDP进行构建。打印头执行过多的启停动作会产生空行程，也会增加打印时间。为了使打印头尽可能少地执行启停动作，可将启停动作设定为负奖励值。同时，为了表明不同启停动作的劣势影响程度，本文使用空行程前后2个节点之间的欧氏距离作为判定标准。除此之外，打印头还要考虑以落下结点为起始点的最大累积转弯奖励值路径，不可忽略后续可达的最大转弯累积奖励。Au的奖励设定如下

式中 Dist（s，¯s）为打印头停止点和开启点之间的欧氏距离，¯s为新状态，¯a为¯s的贪心动作，λ 为调节因子。λ 用于调整Ac转弯奖励值与Au启停奖励值的相对大小，根据打印机的机械性能设定。

Au的动作选择策略也使用ε-greed 函数，动作概率与Ac的设定一致，随机动作为随机选择切片中一个未访问的打印点，贪心动作为选择一个最大奖励值未访问的打印点。构建Au的动作价值函数Qu（s，a），它的定义为Au从当前状态执行转弯和启停的贪心组合策略得到累计奖励的折扣值。更新方式如下

式中sn为沿着新状态¯s的P¯s所到达的下一个状态，¯a为sn的贪心动作。

同理，Qu（s，a）迭代多次后收敛于（s，a）。它是Ac和Au学习成果的归并。Au将多个Ac输出的最优子路径片段合理连接，得到整个切片的最优打印路径，并储存在（s，a）中。

具体算法流程如下：1）构建并初始化Ac和Au的动作价值函数及初始状态s；2）使用ε-greed贪心策略获取动作a；3）据动作a到达新状态¯s，计算Ps和得到sn；4）据式（4）更新Qu（s，a）；5）更新状态s；6）重复步骤（2）～步骤（5）至Qu（s，a）收敛；7）得到最优打印路径。

2 实验结果

以熔融沉积成型（fused deposition modeling，FDM）技术举例说明，所有实验均在CPU 为Intel®CoreTMi5-9400F 2.90 GHz、内存为16 GB的Windows10 电脑上进行编译。本文算法的程序由Python编程语言实现，在百度AI Studio提供的云平台3进行编译和调试。选用FDM 打印机打印模型，打印机的型号为MakerBot Replicator 2，打印材料为PLA，材料直径为1.75 mm。2 个Q-learning 中的ε 均设置为0.5，式（1）～式（4）中参数取值：λ ＝1.0，γ ＝1.0。

2.1 薄壁模型

针对2个复杂程度不同的薄壁模型，将王祎等人提出的Q-path算法［16］和本文算法在转弯次数和启停次数两方面做对比实验。薄壁模型的复杂程度N是由正方形数量表示的，如图2所示。

图2 2 种复杂程度的薄壁模型

2种算法对不同复杂程度的薄壁模型统计结果如图3所示。Q-path算法与本文算法在转弯次数相差很小，这表明二者所得到的路径规划在转弯次数均已达到最优结果。但在启停动作中，相较于固定选择距离最近结点的Q-path算法，本文算法对于结点选择策略具有整体性的考虑，能对较优的结点作出选择。算法思想是将转弯和启停2个动作分解并分别用Q-learning学习。

图3 2 种算法在不同复杂程度薄壁模型中的对比

2.2 轻量化填充模型内部对比

对一般的空心模型内部进行三角形填充，填充密度为5%，层高设置为0.2 mm。实际打印中，一方面要减少轮廓打印的影响，另一方面考虑到模型打印效率和成型精度。统一将内部路径打印速度设置为4 200 mm／min，轮廓打印速度设置为1200 mm／min，空行程的速度设置为9000 mm／min，与Slic3r软件和Cura软件做对比实验。

实验分别打印了Bunny、Buddha head、Kitten、Totoro、Lobster 5个模型的横截面进行展示，如图4 所示。根据这5组模型实体截面打印效果，可以看出，Slic3r 软件和Cura软件打印模型内部有明显由空行程产生的拉丝现象以及材料堆积。本文方法在路径规划时减少了打印头的启停次数，降低了打印过程中模型内部产生空行程带来的影响。

图4 实体截面（左：本文算法，中：Slic3r软件，右：Cura软件）

2.3 打印结果

由表1和表2 统计结果可以得出，5 个实验模型使用本文算法与Slic3r软件和Cura软件规划的路径相比，打印头转弯个数减少率均达到10%以上。打印过程中启停次数减少百分比均为80%以上，这表明本文算法在路径规划过程中有效地降低了打印头执行转弯和启停动作的次数。

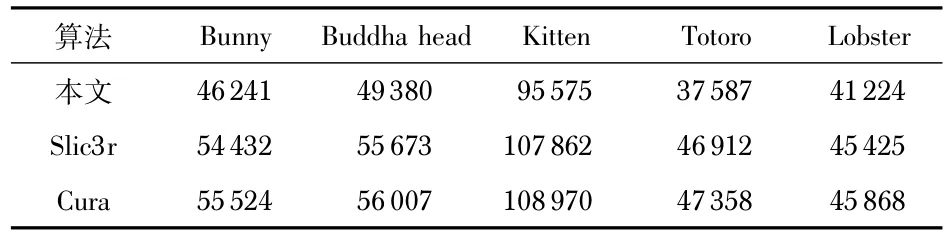
表1 转弯次数

表2 启停次数

Slic3r软件和Cura 软件都是沿着轮廓添加的曲线，本文算法会选择性地沿轮廓添加曲线；其次，3 种算法路径规划中转弯动作、启停结点的选择不同，导致添加的路径长度是不同的，进一步使打印模型的耗材总长度也不同。由实验数据表3可知，本文算法打印模型所用材料长度要小于Slic3r软件和Cura软件。由于Slic3r软件规划路径打印头的启停次数多于Cura 软件，所以耗材长度相对较少。综上，本文算法在保证路径具有最大连续性的前提下，使用打印耗材最少。

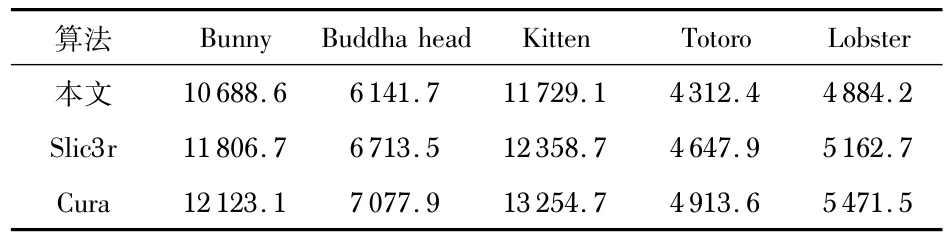
表3 3 种算法耗材长度对比mm

由表4 可以看出，实验中的模型打印总时间与Slic3r软件相比，本文方法规划的路径效率提升均超过10%；与Cura软件相比，前4个模型提升效率也达到了10%以上；只有Lobster 模型效率提升较低，由于Lobster 模型上部爪子部位基本没有内部填充，只是打印外部轮廓，存在较多无法避免的空行程，节省时间的效果不明显。

表4 模型打印时间min

3 结 论

本文针对3D 打印路径规划问题，基于Q-learning 算法，把打印头视为智能体，寻找给定条件下的最优路径。该算法设置约束条件以此优化打印性能，把填充轻量化结构的模型所有层作为一个整体，使用Q-learning 算法寻找模型切片在约束条件下的最优路径规划方案。根据打印实验结果，与现有的商业软件Slic3r 和Cura 相比，该方法可以减少打印头的转弯和启停次数，有效提升了打印效率。