直击本质 触类旁通
刘静

本章内容与实际问题紧密相连,因此问题的背景会千变万化,问题的表述也会千差万别。但面对实际情境,我们只要抓住本质,便能将知识迁移到不同的问题中,做到举一反三,触类旁通。
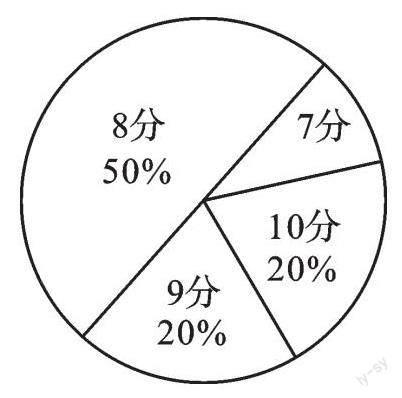
情境:某校七、八年级开展了一次实践活动,对学生的活动情况按10分制进行评分,成绩(单位:分)均为不低于6的整数。现从这两个年级各随机抽取10名学生的活动成绩作为样本进行整理,并绘制统计图表,部分信息如下:
问题1:样本中,七年级学生的活动成绩为7分的有几人?
【解析】由扇形统计图可得成绩为7分的学生数:10×(1-50%-20%-20%)=1。
問题2:你可以从哪些角度分析这组数据?
【解析】可以分析这组数据的集中趋势。因为一个数出现的次数或者这个数所占的百分比都可以表达这个数的重要程度——“权”,所以可以这样理解:扇形统计图中的百分数是对应分数的“权”,则平均成绩为:7×10%+8×50%+9×20%+10×20%=8.5(分)。将这组数据按从小到大顺序排列,因为共有10个数据,第5和第6个数据都是8,所以中位数为[8+82]=8。10个数据中,8出现5次,出现的次数最多,所以众数是8。当然,我们从扇形统计图中也能直观地看到8占50%,权重最大,所以众数为8。
问题3:如果七年级共900人,你能估计全年级的情况吗?
【解析】用样本的平均数、中位数、众数可以估计总体的相关情况。
问题4:若小明记录数据时,误将一个8分写成9分,这对这组数据的集中趋势会产生哪些影响?
【解析】这组新数据的平均数比原数据的平均数大,新数据的中位数变大为8.5,众数不变。
情境:再看八年级10名学生活动成绩统计表:
已知八年级10名学生活动成绩的中位数为8.5分。
问题5:求a、b。
【解析】将八年级10名学生的活动成绩按从小到大顺序排列,它的中位数是第5和第6个数的平均数,由此可知这两个数的和为8.5×2=17=8+9,所以第5、第6个数据分别为8、9,则成绩为8分的有2人,成绩为9分的有3人,即a=2,b=3。
问题6:若七、八年级各增加一个学生成绩:8分,那么这两组数据的平均数、中位数、众数会发生改变吗?若想要七年级(八年级)学生成绩的中位数(平均数或众数)不改变,你觉得添加一个成绩可以是多少?
【解析】两组数据的平均数都变小。七年级组的中位数不变,八年级组的中位数变为8。七年级组众数不变,而八年级组的众数变为8和9。若添加的数使得排序后“中间”的数不变,那么中位数不改变;若添加与平均数相同的数据,那么平均数不改变;若添加的数使得出现次数最多的数不变,那么众数不变。
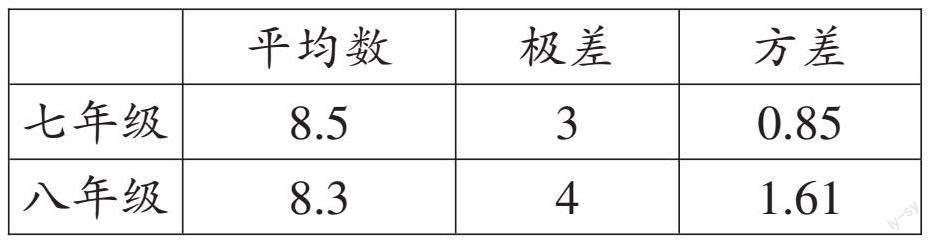
问题7:对七、八年级的成绩,说说你的想法。
【解析】可以用极差和方差描述数据的离散程度。
由此可知七年级的极差、方差较小,数据更稳定,学生成绩相对集中。
问题8:还有没有其他角度分析数据呢?
【解析】比如,活动成绩不低于9分为“优秀”,那么七年级的优秀率为[2+210]×100%=40%,八年级的优秀率为[3+210]×100%=50%。从这个角度可以说明八年级优秀率更高。
(作者单位:江苏省南菁高级中学实验学校)

