数据时代,你准备好了吗?
姜鸿雁

随着互联网时代的到来,历史的车轮轰轰烈烈地“滚进”了数据时代。数据影响着人们每天的衣食住行,我们该如何面对这些数据呢?现从一个简单的问题说起。
A市体育局对甲、乙两名运动员进行一段时间集训,会根据训练情况,及时调整训练方向,以便挑选更优秀的选手参加省赛。小明的爸爸是他们的射击教练,他与小明交流如何进行最后阶段的训练。正在上九年级的小明运用所学的统计知识提出了他的观点,我们一起去看看。
一、收集整理数据
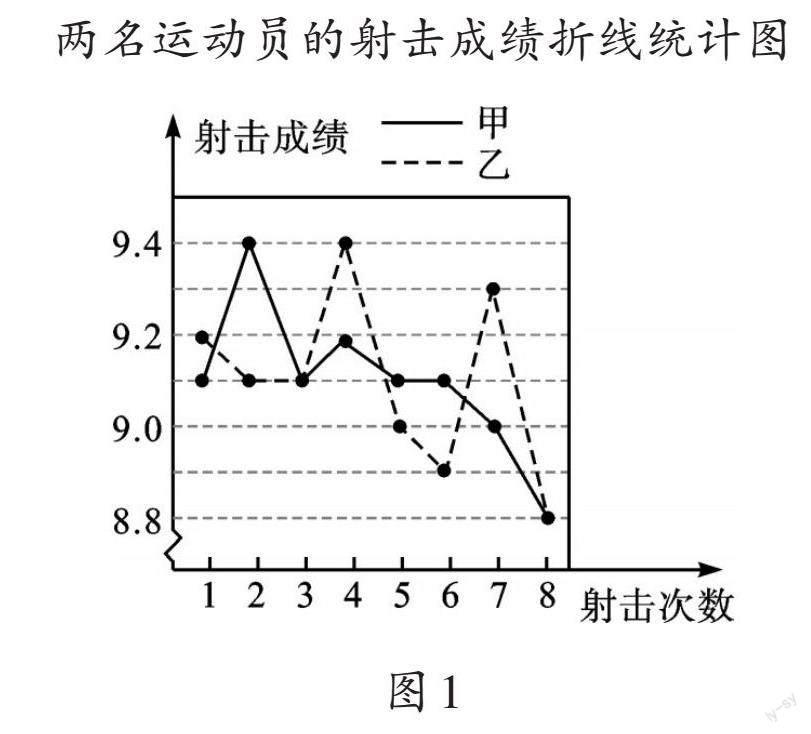
在同等条件下,小明的爸爸对甲、乙两名运动员集训一段时间后的成绩做记录,重点分析他们最近的8次射击成绩(单位:环)。小明建议爸爸用折线统计图整理这8次成绩(如图1)。你認为小明可能给爸爸提出哪些建议和意见呢?
二、分析数据
先了解两名运动员的平均射击水平。分别计算他们的平均成绩:[x]甲=(9.1+9.4+9.1+9.2+9.1+9.1+9.0+8.8)÷8=9.1(环),同理,[x]乙=9.1(环)。此外,我们还有另外两种计算平均数的方法。同学们可以阅读本期第43页的《分析数据,用数据说话》一文,再回来思考。
从平均成绩看,两名运动员的平均水平相当,选谁呢?我们知道,当一组数据中出现“极端”值时,平均数并不能较好地反映一组数据的“集中趋势”,可以刻画一组数据“集中趋势”的还有众数、中位数。两名运动员多数情况下的射击成绩(众数)也均为9.1;如果把成绩按从小到大的顺序排列,可得射击的“中等水平”(中位数),发现中位数仍均为9.1!难道两名运动员的射击水平没有差异?
除平均水平外,临场稳定发挥,也是一名优秀运动员应具备的心理素质,所以我们还得看射击成绩的波动大小,也就是“离散程度”。“离散程度”常用极差和方差来刻画,其中极差只关注最大值与最小值,方差则关注每一个数。我们发现,甲、乙成绩的极差相同,那么,算方差更为合适。因为[s2甲]=0.025,[s2乙]=0.035,所以甲发挥得比乙更稳定一些。
三、作出抉择
小明还认为,可以通过折线统计图直观地看出甲的波动相对小一些。因此,在统计学中,我们同样能够感受到“数形结合”的力量。至此,小明的建议是选择甲参赛更稳妥。
作为经验丰富的教练,小明的爸爸仔细观察折线统计图,有不同于小明的观点:甲总体水平不错且相对稳定,但随着集训时间的推移,后期状态下降态势比较明显,可能心理压力大,影响发挥;乙的射击水平确有波动,但总体呈上升趋势,因此,乙存在较大的“可塑性”和“爆发力”,这也是一名运动员重要的参赛素质。在所剩不多的集训时间内,爸爸将针对两名运动员的实际情况,为运动员“量身定制”训练方案,以便更合理地确定参赛选手。
四、 数学原理
同学们,统计学研究的对象是数据,通过对两组各8个数据的分析,我们不难总结出研究本章知识的流程,如图2:
大数据时代已经到来,如果面对成百上千甚至更多的数据,我们将如何收集、整理并科学分析数据呢?同学们,更多的统计知识等待我们去学习、思考并应用,你准备好了吗?
(作者单位:江苏省无锡市蠡园中学)

