列表格与画树状图怎么选

刘玉兵

在学习“等可能条件下的概率”这一章节时，你是否为选择画树状图还是选择列表格而纠结困扰过？下面，我们就结合几道例题一起感受该如何选择。

一、如果试验结果分为两步，并且所有等可能的结果数较少时

例1 扬州是个好地方，有着丰富的旅游资源。某天甲、乙两人来扬州旅游，两人分别从A、B、C三个景点中随机选择一个景点游览。请用画树状图或列表的方法，求甲、乙两人中至少有一人选择C景点的概率。

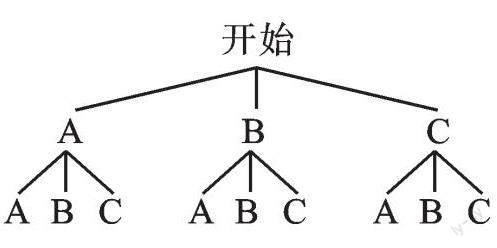
【解析】根据题意，画树状图如下：

或列表格如下：

由树状图或表格可知共有9种等可能的结果，其中甲、乙两人中至少有一人选择C景点的情况有5种，所以甲、乙两人中至少有一人选择C景点的概率是[59]。

二、 如果试验结果分为两步，并且所有等可能的结果数较大时

例2 （苏科版数学九年级上册第139页第8题）抛掷一枚质地均匀的骰子2次，朝上一面的点数之和可能有哪些？它们是等可能的吗？点数之和为8的概率是多少？点数之和为多少时概率最大？

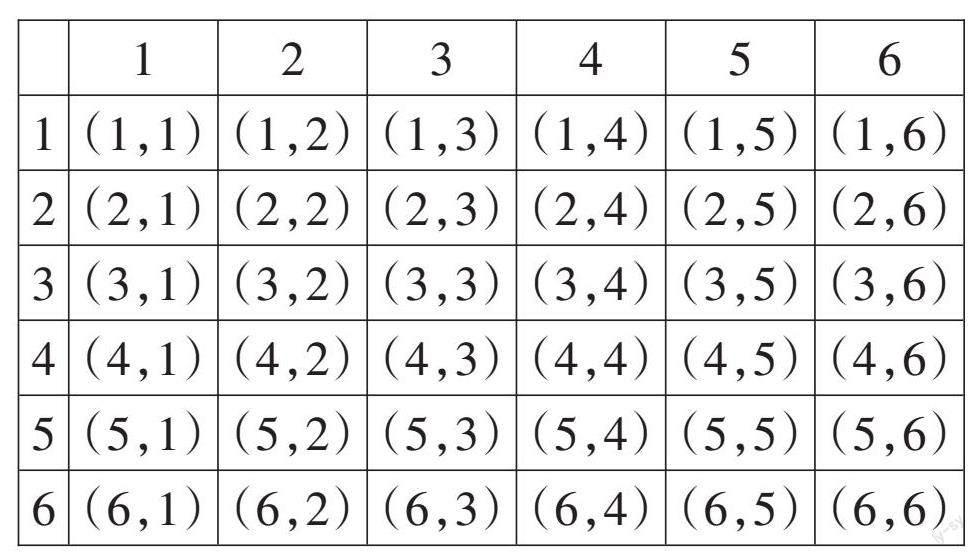
【解析】用表格列出所有可能出现的结果：

朝上一面的点数之和的结果可能有：2，3，4，5，6，7，8，9，10，11，12，它们不是等可能的。在所有可能出现的结果中，出现点数之和为8的结果共有5种，因此P（点数之和为8）=[536]。点数之和为7的概率最大，P（点数之和为7）=[636]=[16]。

这道题也可以利用树状图来找出所有等可能的结果，但较为烦琐，没有表格明了。

三、如果试验结果分为三步及以上时

例3 （苏科版数学九年级上册第139页第9题）小明每天骑自行车上学，都要通过安装有红、绿灯的3个十字路口。假设每个路口红灯和绿灯亮的时间相同，小明从家到学校，通过这3个十字路口时至少遇到1次紅灯的概率是多少？没有遇到红灯的概率是多少？

【解析】用树状图列出所有等可能出现的结果：

所以P（经过3个十字路口至少遇到1次红灯）=[78]，P（经过3个十字路口没有遇到红灯）=[18]。

此题试验分三步，画树状图比较方便，若列表格则比较困难。

看完上面的介绍，想必同学们对如何选择已有所感悟。请同学们尝试做一做以下练习：

1.现有A、B、C三个不透明的盒子，A盒中装有红、黄、蓝球各1个，B盒中装有红、黄球各1个，C盒中装有红、蓝球各1个，这些球除颜色外都相同。现分别从A、B、C三个盒子中任意摸出一个球，摸出的三个球中至少有一个是红球的概率是。

2.把标有号码1、2、3、4、5的5个乒乓球放在一个箱子中，摇匀后，从中任意取一个，记下号码后放回摇匀，再从中任意取一个，则两个号码之和大于2的概率是。

（作者单位：南京师范大学第二附属初级中学）