融入新时代中国精神的高职应用专业教改实践

苏丹

摘 要：为了适应时代的发展需要，以及中国特色社会主义建设的战略需要，高职应用数学教学与新时代中国精神相融合刻不容缓。根据高职应用数学课程中的实际情况，从教学内容、学情分析、教学目标、教学过程和教学评价等方面，探讨了在数学课程中融入“中国精神”的课程思政教学设计的结构框架，并给出导数与两个“中国速度”案例教学课程思政的可行性。

关键词：中国精神； 数学育人；导数与中国速度

中图分类号：F27     文献标识码：A      doi：10.19311/j.cnki.16723198.2023.24.030

人无精神则不立，国无精神则不强。“中国精神”就是以爱国主义为核心的民族精神，以改革创新为核心的时代精神。如果能把“中国精神”融入高数的教学中，不仅有利于让学生培养爱国情怀、民族自豪感，而且能提高学生学习高数的兴趣。因此，通过讲述导数与“中国速度”的实际案例，在课程教学中渗透思政教育，使思政教育与专业知识传授有机融合，挖掘高等数学中相关思政元素对于培养学生正确的世界观、人生观和价值观具有重要意义，从而让学生更有信心应用数学解决其他专业的实际问题，更有利于发挥课堂思政的育人功能。

百年大计，教育为本。课程思政不仅是一种教学理念，更是一种教育方法。课程思政教学是将思想政治元素融入到各门课程中去，使各类课程与思想政治课共同发挥育人作用，最终实现立德树人的目的。以逻辑推理为主的“硬核”的数学课程，就很难和思政教学浑然一体。所以，我们在教学实践中要潜移默化地将“中国精神”渗透到高等数学的教育实践之中，充分运用鲜活的资料，开展教学思政探索。近年来，已有大量文献表明高职应用数学基础课程思政的实践和探索正在进行，如：陈亮探讨了将高职数学与中国传统文化进行融合，实现学生的素质教育和综合能力；赵永辉论述了通过应用数学典型情境中的数学之美使学生认识到数学的实用价值；王慧等提出在数学分析课程中融入课程思政的途径。本文将从以下几个方面探讨高职应用数学课程思政的结构框架。

1 教学内容

微积分内容是理工类专业学生进行专业学习的重要工具和基础。而导数概念是微积分的重要部分，其概念虽然比较难理解，却非常有用，是学习其他各类学科的重要辅助工具，对学生后期发展有极大的作用。

该课程设计目的是通过深入剖析学校思政教育活动的具体实践，并结合导数定义在思想教育活动中3个恰当的时间节点上，不着痕迹地渗透“中国精神”。首先，感受和认识“中国速度”。其次，用发展的唯物主义观点“看”数学。最后，学会学以致用来完成“互动接收”。

2 学情分析

学习本课程前需掌握函数的概念、极限的概念与思想，以及在初高中就学过的计算平均速度、圆的切线等知识，从而为本节课的学习奠定基础。由于导数的概念比较抽象，直接给出导数定义是不可行的。因此，在教学前，先让学生自行查找和上传“中国速度”的相关视频，调动学生的学习兴趣。并将学生熟悉的短跑飞人苏炳添和中国复兴号的视频背后的实际数学问题—瞬时速度和曲线切线，作为“中国精神”融入数学案例教学过程的典型代表。引导学生对以上的两个“中国速度”的案例进行观察、归纳，总结出它们的共同特性，最后教师抽象概括出导数的概念，让学生体会“中国速度”背后的“中国精神”，使学生充分树立对“改革创新是新时代的迫切要求”的科学认识，增强责任感、夯实创新基础，大胆投身改革创新实践。

3 教学目标

从认识上，通过对两个“中国速度”的案例剖析，可以经历从平均变化率转换到瞬时变化率的过程，从而掌握了导数定义的实际背景，并明白了瞬时变化率就是导数。在能力上，学会使用逼近方法、类比方法；学会解决其他专业的实际问题，例如化工专业中的瞬时反应速率、用料最节省等实际应用问题。在素质上，培养学生敢于突破自我的拼搏精神；培养学生的爱国情怀、民族自豪感。在教学过程中，选出两个有代表性的“中国速度”的视频，进行案例教学，引导学生观察、思考，并尝试进行归纳总结两个案例中的共同特征，从而引导学生攻克导数概念的重、难点。

4 教学过程

4.1 课前云端预知

在课堂教学前，教师可在职教云平台发起实验任务，以“中国速度”为关键词，搜索相关视频并上传到智慧职教平台。引导学生搜集相关资料，并思考以下的两个问题。

（1）运动员苏炳添在百米比赛时，某时刻的瞬时速度如何求？

（2）当中国名片复兴号在行驶转弯时，要使中国高铁复兴号安全稳定地运行，转弯设计会涉及到切线斜率问题，切线的斜率怎么解决？

通过创设问题情景，提升学生对中国科技发展的关注，增强学生的民族自豪感和爱国情怀。

4.2 课中案例驱动

线下课程在多媒体教室进行，从大家上传到职教云平台有关“中国速度”的视频中，选出2个具有代表性的案例：“奥运英雄”—苏炳添和“中国名片”—复兴号，进行下面的案例教学。

案例1“奥运英雄”——苏炳添

2020年东京奥运会的男子个人百米淘汰赛上，运动员苏炳添以9秒83的速度突破亚洲纪录，成为第一个进入奥运会男子“飞人”决赛的中国人。也是电子计时时代第一位闯入奥运百米决赛的亚洲选手！通过观看奥运英雄苏炳添百米比赛视频，让学生体会努力拼搏，不给自己的人生设限，努力挖掘自身潜力，敢于突破自我的拼搏精神。案例教学中融入“中国速度”，同时也增强学生的爱国情怀和民族自豪感。

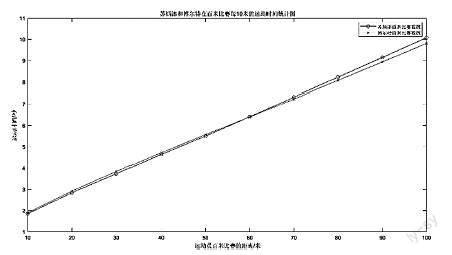
如何求解奥运英雄蘇炳添在百米比赛时，某时刻的瞬时速度？我们可以根据2016年里约奥运会，我国运动员苏炳添和牙买加运动员博尔特百米比赛的数据，进行分析。通过从国际田径业余联合会（IAAF）官方网站上获取的这两名选手参赛视频，利用Dartfish软件，为他们的前10秒做了报秒计算，并通过Matlab等软件制绘出了他们的折线对比图（见下图）。

由此，可以看出，运动员苏炳添在前1/3段路程中，比运动员博尔特运动得快；博尔特在后2/3段路程中，比苏炳添运动得快。我们通常用平均速度来比较运动员运动的快慢。这就给出一个求解思路，若要求解变速直线运动的瞬时速度问题，可以引导学生通过平均速度来求解，也就是用已知的知识来探究未知的知识。求苏炳添在某时刻的瞬时速度，把运动员苏炳添看作是一个质点，设质点做变速直线运动，其位移函数为s=st，如何求得t0时刻的瞬时速度？

为了求t0时刻的瞬时速度，可在t0附近取一点t，将t0到t这段时间间隔记作Δt。因此，这段时间间隔内的平均速度就可以得出。平均速度等于这段时间所经过的路程除以这段时间间隔，即v=st－s（t0）t－t0。当时间间隔变得非常非常小的时候，也就是Δt→0时，t无限接近t0，那么平均速度v-就无限接近t0时刻的瞬时速度。根据极限的思想：逼近的思想，我们可引入极限的概念，用平均速度近似的表示瞬时速度。若平均速度的极限存在，那么该极限就是t0时刻的瞬时速度。

案例2 “中国名片”——复兴号

新一代标准高速动车组“复兴号”是中国自主研发、具有完全知识产权的新一代高速列车，它集成了大量现代高新技术，牵引、制动、网络、转向架、轮轴等关键技术实现重要突破，是中国科技创新又一重大成果。至2016年7月，中国标准动车组已在世界上率先进行时速420千米的交会与重联运行测试；2017年6月25日，中国标准动车组被官方正式命名为“复兴号”。 2017年9月21日，中国高速铁路实施了最新的列车运行图，国内“复兴号”动车组在京沪高铁率先恢复350公里航速运行，我国再次变成当今世界上动车商业运营效率最快的国家。通过观看学生自行查找的复兴号的视频，体会“中国速度”之快。我国创新能力的标志性成果之一——高铁，党的十八大以来，习近平总书记在出访时，曾多次向世界展示过这张“中国名片”。

当高铁驶入弯道时，为保持其平稳运行，弯道设计会涉及到曲线在某点的斜率，那么如何求解曲线的切线斜率？

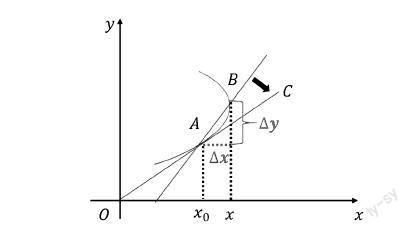
为了求曲线的切线斜率，可以从已经学过的知识去探究，可以通过割线的斜率来求解切线斜率。在A点附近取一点B，B也是曲线一点，链接AB得到一条割线。割线的斜率就可以表示为kAB=tanα=ΔyΔx=y－y0x－x0，（其中，α是割线与x轴正方向的夹角）。当B点沿着曲线向A点无线靠近，Δx→0时，割线AB斜率就可以近似地表示切线AD斜率。同样的，根据极限的思想，在这里也引入极限的概念，用割线AB斜率近似地表示切线斜率。

通过对以上的两个“中国速度”的引例的探究，可催化引导学生进行观察、分析、归纳和总结它们之间的相同点，提升学生思辨能力。可以看出，虽然的它们的实际意义不同，但最终得到的表达式的结构是相同的。无论是求奥运英雄苏炳添在某时刻的瞬时速度，还是求中国名片复兴号在驶入弯道时，某点的切线斜率，最后得到表达式的结构都是：平均变化率的极限。由此可引入导数的概念，即定义。

定义设函数y=f（x）在点x0处及其附近有定义，如果极限

limx→x0ΔyΔx=limΔx→0fx0+Δx－f（x0）Δx=limx→x0fx－f（x0）x－x0，

存在，则称函数f（x）在点x0处可导，并称此极限值为函数f（x）在点x0处的导数，记为f′（x0），即

f′x0=limx→x0ΔyΔx=limΔx→0fx0+Δx－f（x0）Δx=limx→x0fx－f（x0）x－x0

函数值与自变量两者改变量的比值ΔyΔx可称为平均变化率，而导数f′（x0）表示函数f（x）在x0处对自变量x的变化率，所以导数反映了函数值随自变量变化而变化的快慢程度，换句话说，导数的实质就是平均变化率的极限。

在案例1中，t0时刻的瞬时速度可表示为s′（t0），其物理意义为运动员苏炳添在t0时刻的瞬时速度。在案例2中，在点A（x0，f（x0））处的切线斜率可表示为f′（x0），其几何意义为高铁行驶弯道时在（x0，f（x0））的切线斜率。

那么函数在某一点是否可导？可通过上式平均变化率的极限进行判断。若上述极限存在，则函数f（x）在点x0处可导；如果上述极限不存在，则称函数f（x）在点x0处不可导。因此导数的定义式不仅用于判定是否可导，还可以用于相关计算。

4.3 课后实践研学

以知促行，激发学生创造力。课后让学生尝试利用导数的定义求解各专业的实际应用问题，导数知识学以致用，从而完成“互动接收”。

例 一级化学反应A+B→C。在某温度时，在2L的密封容器中，A和B的初始浓度相同：A=B=amol/L.则C=a2ktakt+2其中k为常数。

（1）求在时刻t的反应速度？

（2）当t→+

浓度会发生什么变化？

（3） 当t→+

反应速率会发生什么变化？

设置小组课后答题任务，让学生尝试给出问题（1）的解题过程，并引导学生探究问题（2）（3）在实际情况中的实用意义。

5 教学评价

构建以学生为主的形成性和多样化的评价系统，有助于探讨与数学有关学科的思政模式。以线上练习、教学互动、期末考试、案例应用为切入点，同时还根据学生的整体学习态度、考试认真程度等的综合分析结果，对平行班级采取图表1中所示的评分系統进行了过程性比较研究，从而为告知学生应用数学的课堂思政的系统性提供了有力保障。

6 结语

立德树人是教育的根本任务。新时期新征程，“中国精神”为讲好思政课提出了丰富多彩、鲜活的事例和材料，我们善用思政材料，深度挖掘课程思政教育功能的具体案例，在教学过程中3个恰当的节点处，将导数定义自然地引入新时代中国精神，通过“理实一体”模式充实对学生的认识，激发学生对思维浓厚兴趣，对学生的思维行为加以引导与教育，实现为国家、为人民、为社会培育德艺双馨应用型人才的教育目的。

参考文献

［1］习近平.在第十九届中央政治局第三十九次集体学习时的讲话[N].中国新闻网，20220527.

[2]张大良.课程思政：新时期立德树人的根本遵循[J].中国高教研究，2021，1（1）：59.

[3]陈超.高职数学教学中渗透中国传统文化的研究[J].当代教育实践与教学研究，2022，5051.

[4]赵永辉，滑会超.高职数学课程思政建设路径探索[J].成才之路，2023，5（14）：2124.

[5]王慧，黄敏，张洪涛;等.数学分析“课程思政”的实践与思考[J].创新教育研究，2019，7（5）：675678.

[6]刘薇，常振海，高忠社，等.融入课程思政元素的导数定义教学设计[J].通化师范学院学报，2021，10（42）：2934.

[7]同济大学数学系.高等数学（第七版）[M].北京：高等教育出版社，2014.