模糊需求下的多中心冷链配送车辆路径问题

王 祺，肖 青

大连海事大学 交通运输工程学院，辽宁 大连 116026

现代社会中，依靠冷链运输的产品数量逐渐增加，配送区域不断扩大，单配送中心模式难以满足物流合理配送规划。同时，低碳是如今社会所倡导的理念，人们对低排放量要求逐渐变高。而冷链产品具有易腐性、时效性以及客户点分散等特征，为了保证产品新鲜度，在运输过程中对时间的要求高、车辆排耗量大。因此，在优化冷链配送模式时，碳排放在车辆路径优化问题中也是不容忽视的[1]。此外，实际配送中，还存在很多不确定性因素，其中客户对冷链产品需求的不确定是配送中考虑模糊变量的重要因素之一。所以，对于冷链物流来说，综合考虑带时间窗的多配送中心下模糊需求车辆路径问题研究（multi-depot vehicle routing problem with time windows and fuzzy demands，MDVRPTWFD）具有更广泛的应用价值。

对于车辆路径优化的相关引申问题，已经有很多学者展开了深入的研究，并取得很不错的研究成果。其中带时间窗的VRP（vehicle routing problem with time windows，VRPTW）最早是由Solomon[2]提出，并且给出不同规模的经典求解算例，他提出的最小成本最邻近法（nearest neighbor algorithm based on minimum cost，

NNC）在构造初始解时，可高效地产生可行解，加速后期算法的迭代优化。李军涛等[3]考虑模糊时间窗的VRP问题，从冷链物流运输角度建立碳排放量、配送成本和客户满意度的多目标优化模型，采用自适应灾变遗传算法进行求解。之后，李军涛等[4]进行VRPTW 问题的延伸，考虑交通拥堵和多车型的车辆路径优化，并将碳排放量转化为成本加入到配送成本中。Xu 等[5]研究单配送中心车辆路径优化，以时变车速下的燃料消耗量和客户满意度为目标，通过自适应和贪心策略的改进非支配排序遗传算法去求解。康凯等[6]构建了单配送中心下考虑碳排放的生鲜农产品运输路径优化模型，并用嵌入2-opt局部搜索算法的改进蚁群算法进行求解。

对于多配送中心的车辆路径问题（multi-depot vehicle routing problem，MDVRP），范厚明等[7]研究时变路网下、混合时间窗的多配送中心VRPTW 问题，并设计自适应遗传-大邻域搜索算法进行求解。辜勇等[8]考虑多中心的协同配送VRPTW 问题，并设计K-mediods 聚类算法、改进的蚁群算法和节约算法的三阶段求解算法进行求解。Zhen 等[9]研究了具有时间窗和发布日期的多车场多行程车辆路径问题，以总旅行时间最小化为目标，提出了混合粒子群优化算法和混合遗传算法求解。

针对模糊变量下的车辆路径问题的研究，范厚明等[10]结合模糊需求和模糊时间窗，去研究VRP 问题，以总行驶距离、车辆数最少以及客户满意度最大为目标，并利用混合遗传算法进行求解。王文君[11]考虑交通流，以车辆固定成本和油耗成本为目标去分析模糊需求下的多车型VRP 问题，通过突变遗传算法和可信性理论约束模型去求解。Nasab等[12]研究的是模糊需求选址路径问题，基于模糊可信性理论去建模，并结合随机模拟的混合模拟退火算法进行求解。

通过分析以往的相关研究，发现有以下不足之处：（1）针对VRP问题，大多数学者考虑的是单配送中心下的路径优化，在城市区域间的多需求下，会导致配送压力过大以及车辆调度失衡，即使有的学者研究了MDVRP问题，但没有去考虑其他不确定因素，目标函数通常研究单一。而且有的学者是将多中心问题转化为单配送中心，比如Zhen等[9]，研究MDVRP 问题，考虑闭环的多中心，即匹配到合适的中心后，必须往返都在该中心下，并没有很好地体现多配送中心资源共享的特征。（2）对于考虑冷链物流配送，在多配送中心基础上，对融入碳排放、冷链运输特性以及配送中的不确定信息研究较少。（3）有很多考虑带时间窗的模糊变量和多中心的VRP 问题，但鲜少将其融入冷链运输中，对冷链运输配送成本分析也不够全面。因此，本文研究在多配送中心冷链运输基础上，对MDVRPTWFD问题展开研究，综合考虑模糊需求、载重量和时间窗约束，构建以车辆的固定成本、运输成本、制冷成本、时间惩罚成本和碳排放成本为总配送成本最小和客户满意度最大的多目标优化模型，通过改进的遗传算法-大规模邻域算法和随机模拟算法进行求解。丰富了不确定性多配送中心下冷链配送车辆路径问题的研究理论，为相关企业提供理论指导。

1 问题分析与模型构建

1.1 问题描述

MDVRPTWFD 问题可以描述为在物流运输网络中，由多个配送中心联合对多个需求不确定的客户进行配送服务，并在给定的目标下，根据载重量、时间窗等约束条件下，合理规划车辆配送路线。其中不同配送中心之间的车辆是可以共享的，不要求每辆车只有一条路径，车辆在完成配送任务后，以及在中途补货，均可选择距其距离最近的配送中心进行停靠或装卸货，然后继续进行配送服务。

本文研究的是冷链物流配送的MDVRPTWFD问题，可以描述为在某个配送区域里，有 ||N个配送中心，配送中心集合为N={n|n=1,2,…,|N|}，M表示客户集合，M={m|m=1,2,…,|M|}，K表示车辆集合，K={k|k=1,2,…,|K|}，|K|表示车辆总数。dij表示客户点（配送中心）i到客户点（配送中心）j的距离；C1表示单位车辆使用成本；C2表示单位距离运输费用；C3表示单位制冷成本；C4表示到达客户点i的开始服务时间在[Ei,ei]内的早到惩罚成本；C5表示到达客户点i的开始服务时间在[li,Li]内的晚到惩罚成本；Ce表示单位碳排放成本；[ei,li]表示节点i的最佳的服务时间窗；[Ei,Li]表示节点i的最大容忍服务时间窗；tijk表示第k辆车从节点i到节点j的运输时间；Qk1表示车辆k运输行驶产生的热负荷；Qk2表示车辆k开关车门装卸货时所产生的热负荷；ti表示节点i的开始服务时间；Cd表示碳排放系数；P1表示单位距离车辆燃油消耗量。

1.2 模型假设

为了更好地解决问题，在构建模型时，提出以下的假设：

（1）多配送中心模式下的冷藏车辆均为同一车型，车辆的装载量、制冷性能、碳排放相关系数以及单位距离车辆油耗消耗量等相关信息已知。（2）车辆可在任意中心出发，完成任务可选择回到距离最近的任意中心，不需要回到原配送中心。（3）配送中心和客户点的位置信息已知，但客户需求量是不确定的。（4）车辆进行配送时以某个平均速度进行配送。（5）一辆车可被调度多次，服务多个客户，但每个客户只能由一辆车进行服务。（6）对冷链物流运输问题，仅考虑制冷成本，不考虑在配送中由于冷链产品变质等因素产生的货损成本，这部分货损体现在时间惩罚成本和客户满意度上。（7）所有配送中心能满足客户需求，不存在缺货情况。（8）对模糊需求来说，在得到初始计划路线和实际需求后，不考虑在配送途中需要返回配送中心补货再返回客户点继续服务后，会违反其最大容忍时间窗，只是相应的客户点的开始服务时间改变了。

1.3 模糊需求分析

由于配送车辆在未到达客户点时，客户需求是不确定的，即模糊需求。所以，引入决策者的主观偏好值和可信性测度理论，在初始阶段，客户需求被看作是三角模糊数，即客户需求qi=(q1i,q2i,q3i)，每辆车有相同的载重量Q，假设某一辆车已经服务p个客户后，由模糊数学知识可知，此时车辆剩余的载重量Up也是三角模糊数，即：

根据可信性理论[13]，对于客户点p来说，其下一个客户p+1点的需求量小于车辆剩余载重量的可信性为：

式（1）中，Cr为满足qp+1≤Up条件的可信度，Cr越大，表明车辆剩余的载重量越有可能满足下一个客户点的需求量，则该客户点被服务的机会越大，故引入主观偏好值Cr*，它表示决策者对车辆是否继续服务下一个客户点的态度偏好，从而规划出相应的初始计划路线。当Cr*取较小值时，决策者倾向于充分利用车辆的载重能力，不怕配送失败的风险；反之，Cr*取较大值时，决策者希望尽可能地规避配送失败的风险，此时车辆剩余载重量满足下一个客户点的需求量的可能性很大，配送失败的可能性小。根据文献[13]知Cr*∈(0,1]。在车辆服务客户的过程中，当Cr≥Cr*时，该车辆继续完成下一个客户的配送任务；当Cr≤Cr*时，该车辆就近返回配送中心停靠，同时距离该配送失败的客户最近的配送中心，开始新派车完成剩余的运输任务；重复上述过程，直至所有客户都被服务。

1.4 模型构建

1.4.1 总配送成本函数

（1）车辆的固定成本Z1。其指的是参与配送车辆的基本保养损耗、司机工资等，与使用的车辆数目有关。

（2）车辆运输成本Z2。本研究主要指的是车辆行驶过程产生的成本，与运输距离呈正相关。

（3）车辆制冷成本Z3。冷链物流配送车辆一般是冷藏车，所以综合考虑车辆行驶过程中和装卸货开门时，为了维持车厢内的低温，车厢的制冷系统产生的能耗。制冷能耗与温差导致的热负荷有关，对于运输途中，制冷成本与厢体隔热壁渗入、厢体漏气以及太阳直射传入车厢体内部的热负荷有关；装卸货时，考虑开门时的厢体隔热壁和太阳直射传入厢体的热负荷，而该部分热负荷与车辆配送时的开门次数所附加的热负荷系数相关。根据文献[14]得出下列制冷成本计算公式：

表1 开门附加热负荷系数Table 1 Additional thermal load factor of door opening

R为车辆传热系数，S1为车厢体受太阳辐射面积，S1=(30%～40%)S，S为车厢传热面积，Tw为车厢外界空气温度，Tn为车厢内的温度，Ty为厢体受太阳辐射后表面的平均温度，Ty=Tw+20，t为车厢体每天受太阳辐射的时间，一般为12～14 h；β为漏热系数，tijk为第k辆车从节点i到节点j的运输时间，tsi为服务客户点i所需时间。

（4）时间惩罚成本Z4。在最大可接受范围内，车辆到达客户点的开始服务时间未在期望时间窗内，会有相应的惩罚成本。

惩罚成本函数：

则时间惩罚成本Z4为：

（5）碳排放成本Z5。冷链配送的车辆比普通货车要消耗更多的燃料，进一步产生大量的二氧化碳，所以考虑碳排放成本是分析冷链配送成本不可缺少的一部分。

则总成本函数F1为：

1.4.2 客户满意度函数

冷链产品配送对时间有严格的要求，时间不仅影响到产品的损耗，从而影响客户对产品的满意程度。

客户i时间满意度函数f(ti)：

所有客户对时间的整体满意度函数F2如下：

1.4.3 目标函数量纲转化

为了方便目标函数标准化转化，把客户满意度函数转化为客户不满意度。

采用模糊数学方法对总成本函数F1和客户不满意度去标量化。冷链物流配送路线的规划对时间要求非常高，即使配送成本很低，但一旦产品腐烂了，客户不满意，那这条路线规划就毫无意义，同时在日益激烈的市场竞争中，较高的客户满意度是冷链企业提高自身竞争力的关键因素之一[15]。故把配送总成本和客户满意度视为同等重要，即赋予相同的权重，让决策者更好地根据自身情况去选择合适的配送路线，此时多目标函数问题也转化为单目标优化问题，，量纲转化后的总目标函数为：

式（15）中，w1为冷链配送总成本的权重系数，w2为客户不满意度的权重系数，w1=w2=0.5。

1.5 约束条件

式（16）表示所使用的每辆车装载量不超过车辆最大装载量的可信性Cr不得小于主观偏好值；式（17）表示每条路径的车辆装载量不得超过其最大载重量；式（18）表示所有配送中心安排的配送车辆数不得超过已有的车辆限制总数；式（19）表示每个客户只能派一辆车服务；式（20）表示车辆到达客户点开始服务时间必须在其最大容忍时间窗内；式（21）表示车辆从某个配送中心出发，中途补货或完成任务停靠，可回到任意中心。

2 算法设计

在某个主观偏好值下，对于模糊需求，通过改进遗传-大邻域搜索算法进行求解得到初始计划路线，然后根据随机模拟算法得到客户的实际需求；在已产生的初始可行路线方案中，根据载重约束，当实际客户需求得不到满足时导致配送任务失败，车辆就近返回配送中心重新装货再返回至任务失败点继续完成剩余任务，此时返回失败点再服务，该点的开始服务时间变了，相应的这条路线运输费、制冷、惩罚成本以及满意度都发生相应的改变；最后，根据调整好的路线利用改进遗传算法进行目标函数分析，从而选择最优的配送路线。

2.1 改进的遗传-大邻域搜索算法

MDVRPTWFD 问题考虑的变量多而复杂，而传统的遗传算法收敛快，使其不能很好地得到最优解。后期嵌入大规模邻域算法是为了防止优化过程中产生大量不可行解，降低求解效率，又避免了局部最优。

2.1.1 染色体编码

本研究采用实数编码，对于MDVRPTWFD 问题里包含|M|个客户，|K|辆车，则定义染色体长度为|M|+|K|-1，定义编号1～|M|为客户点，大于|M|的数字编号作为路径的分割点。例如假设有8个客户，4辆车，编码形式如图1（a）；如果添加的分割点不能补齐个体染色体长度，则后面继续添加大于| |M的数字来补齐，如图1（b）；这样根据分割点可以划分不同的配送路径，再进行路径首末配送中心的匹配。

图1 染色体编码示意Fig.1 Chromosome decoding diagram

对于图1（a）可以看出使用了3辆车，配送路径为1-4-5，7-8-2，3-6；然后根据已有的配送中心，进行路径首末客户点距离最小匹配。

2.1.2 初始种群的生成

在生成初始种群之前，先构造MDVRPTWFD 问题的初始可行解，本文基于最小成本的最邻近法[2，16]、载重的可信性约束以及时间限制约束来构造高质量的可行解，然后将初始解合并生成初始化种群。采用上述编码例子图1（a），构造的可行初始解为1-4-5，7-8-2，3-6；将其合并后用9～11 的数字编号来分割，即初始路径合并后的初始种群为1-4-5-9-7-8-2-10-3-6-11，再对其进行交叉、变异、选择以及局部搜索操作。

最小成本的最邻近法（NNC）的步骤如下：

步骤1派出一辆车进行配送，关于起点选择，文献[2，16]是从配送中心出发，本文是在未访问的客户点中随机选择一个节点开始遍历搜索，该客户点是满足时间窗要求，若不满足则换一个客户点。

步骤2在未访问的客户点中，选择满足约束条件的“距离成本”最小的节点，来插入到当前车辆路径中。

步骤3重复步骤2，若违反载重可信性或时间约束，把当前路线存储后，新派一辆车，重复步骤1、2、3的步骤；若所有客户点被服务，则结束。

具体流程如图2所示。

式中,Aij为客户i，j的时间窗接近程度，指的是后一个节点的开始服务时间与前一个节点的完成服务时间之差；Uij表示客户j的时间紧迫性，指的是客户点j的最迟服务时间与其开始服务时间之差；tij为客户点i到客户点j的运输时间；Dij为客户点i，j之间的距离成本，其大小用来衡量下一个客户点的选择，α1、α2、α3是大于0的权重系数，α1+α2+α3=1。

2.1.3 适应度函数确定

传统的适应度函数计算是按比例计算的，在优化过程中会陷入局部最优，引用文献[17]中的适应度计算方法，将其变得具有随机性。

F(x)表示个体x的目标函数值，G(x)表示个体x的适应度值；为了防止式（25）无意义，同时也在遗传操作中更直观地比较适应度值大小，λ取（0，1）之间任意正实数[17]。

2.1.4 遗传操作

（1）改进的交叉操作：以构造的可行初始解来初始化种群，生成的是一模一样的种群个体，导致传统的交叉操作不能适用了；所以根据交叉概率，先通过一定的改进手段使所有种群不同化，再采用部分映射交叉[18]。具体改进方法如下：首先在种群里，根据个体顺序和交叉概率，依次去选择两个父代A、B，然后随机生成两个交叉点，将父代A 的交叉片段放到父代B 的尾部，父代B的交叉片段放到父代A的首部，删掉不是交叉片段的重复基因，这样就产生了差异化的父代个体，方便后续采用部分映射交叉，来产生新的子代。

（2）变异操作：采用逆序变异，根据变异概率去确定要变异的个体，随机生成两个变异点，将两点之间的基因逆序生成新的个体。例如，[2 3 4 8 1 10 7]→[2 1 8 4 3 10 7]。

（3）选择操作：采用轮盘赌和精英保留策略相结合的方法进行选择操作，其中精英保留策略是父代种群最优值与新种群最优值比较，选出当前种群的最优值；其次用父代种群的最优解替换新种群中最差的个体，再进行下一代的遗传操作。

2.1.5 大规模邻域搜索

遗传算法在逐代优化过程中，初始可行解的基因已经被分解，重新解码的路径组合，存在大量不可行解，会导致收敛过快，陷入局部最优，不能得出最好的最优值。而大规模邻域搜索算法（large neighborhood search，LNS）是对路径间邻域进行破坏修复，简单来说就是使用破坏算子在当前解中移除若干个客户，然后再使用修复算子将移除的客户重新插入到被破坏的解中，从而获得新的可行解。

（1）破坏算子

①载重约束移除算子。对当前路径的客户点进行逐步检查，由于当前路径是在模糊需求情况下产生的，则对路径中的每个客户点进行载重约束可信性判断，然后把该个体的每条路径中不满足可信性约束的客户点储存。②时间窗约束移除算子。在载重约束移除算子的基础上，还会存在路径中某个点违反其最大容忍时间窗的情况，把违反的点储存起来。

在使用以上两个破坏算子后，可能原路径上的客户点被全移除了，则需要把路径中可能为空的路径删除。

（2）修复算子

最优距离插入算子：在满足所有的约束条件基础上，把每个移除点依次插入到路径各个空隙，再计算此时的路线匹配中心后的距离增量，若存在合理的插入点，选出最小距离增量对应的插入点和插入位置，否则新派一辆车。所有移除点选好最优的插入位置后，采用最远插入启发式来选择哪个移除点先插入，然后把插入完成的点删除，重复以上所有步骤，直至所有移除点全被插入到路径中。其中最远插入式启发式是将移除客户点中最优插入距离增量中最大的选出来，其对应的移除点先被插入，这样的做法是为了在插入时有随机性。

2.2 随机模拟算法

步骤1在客户的模糊需求范围内随机生成一个数δ并计算其隶属度u(δ)，其中将q2i设置为qi，模糊需求范围为((1-r)qi,qi,(1+r)qi)，取r=0.2。

步骤2在[0，1]范围内随机生成一个数δ1。

步骤3若δ1≤u(δ)，则δ作为该客户的模拟需求量，否则重复以上步骤，直至满足要求。

步骤4重复步骤1～3，使所有客户模拟得到实际需求量。

3 算法验证与算例分析

3.1 算法验证

采用MATLAB R2016b进行算法编程，操作系统为windows10。不考虑模糊需求，利用本文的算法去解决文献[19]的算例，文献[19]是使用MDVRPTW 标准算例pr01，48 个客户点，4 个配送中心；运行10 次，取最优解与文献[19]的蚁群算法所得结果对比见表2。

表2 与文献[19]的结果对比Table 2 Contrast with result of literature[19]

由表2 可知，在模型相同的条件下，本文算法求出的最优解使用的车辆数是8，比文献[19]多3 辆，因为文献[19]考虑在配送时，车辆可以中途回到配送中心补货，而本文算法思想是超过载重约束时，就返回任意中心，重新派车服务。但在成本方面，本文算法要优于文献[19]，总配送成本减少7.3%，实验结果证明了本文算法设计是合理有效的，并且同样具有很好的寻优性能，两算法求解的最优路线对比具体见表3，其中49～52 表示配送中心，本文算法求解的最优路径如图3。

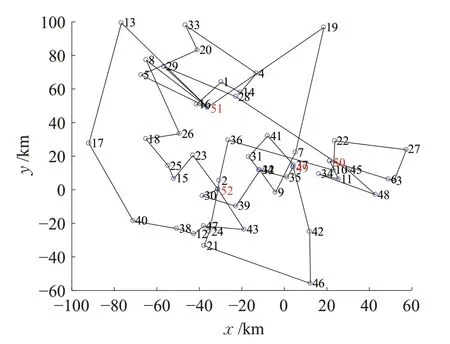
图3 pr01算例的车辆路径图Fig.3 Vehicle path map of example pr01

表3 配送路线对比Table 3 Comparison of distribution route

3.2 算例分析

3.2.1 算例描述

假设某企业有3个货物充足的物流配送中心，20个客户点，其中每个配送中心有5辆型号相同的车辆，车辆最大载重量Q为3.5 t，配送中心之间的车辆是共享的，且总的车辆数最大为15。车辆平均速度v为40 km/h，每辆车的使用成本为300 元/辆，单位距离运输费C2为5 元/km，制冷成本C3为11 元/kcal，漏热系数β为0.25，车辆传热系数R为0.3 kcal/m2·h·℃，车厢传热面积S为35.77 m2，夏季车厢外界空气温度Tw为32 ℃，车厢内温度Tn为5 ℃，厢体每天受太阳辐射时间t为13 h，早到惩罚成本C4为6元/h，晚到惩罚成本C5为11元/h，单位碳排放成本Ce为0.2 元/kg，二氧化碳排放系数Cd为2.65 kg/L，单位距离燃油消耗量P1为0.16 L/km，车辆每天早上6点从配送中心出发。算法参数设置如下：种群大小取100，最大迭代次数取200，交叉概率Pc=0.7，变异概率Pm=0.3，λ=0.2；经多次测试，最小成本的最邻近法中α1=0.5，α2=0.3，α3=0.2。配送中心和客户点的位置是在[-100，100]范围里随机生成的，具体信息见表4，其中编号1～20为客户点，21～23节点表示配送中心。

表4 客户和配送中心信息表Table 4 Customer and distribution center information sheet

3.2.2 运行结果分析

为了验证多配送中心在冷链物流配送中的有效性，将单配送中心与多配送中心配送模式进行对比分析，设置以上算例中编号23 为单配送模式的中心，主观偏好值=0.3，运行10次，取最优解，两模式对比分析情况见表5，而表6和图4分别为多配送中心模式下的最优路线和最优路径示意图。

从表5 可以看出两配送模式所派的车辆数是一样的，客户满意度相差不大，但在配送成本方面，多配送中心模式使运输总成本降低了23.24%，完成运输任务的总距离减少了28.68%，总目标函数值减少了18.27%；多配送中心能共享资源，大幅度减少车辆往返距离，从而降低配送成本。因此在配送成本和客户满意度同等重要情况下，多配送中心配送模式要优于单配送中心模式。

其中图4 的虚线部分表示在考虑模糊需求的情况下，该路径得知实际需求后，发生配送失败，就近返回中心补货了，实线则是没有发生配送失败情况。

3.2.3 算法对比分析

以相同的参数设置条件，采用普通遗传算法进行多目标冷链物流模糊机会约束模型求解，运行10 次，取最优解，求解结果是派遣8 辆车，最优配送成本为151 130.62，客户满意度为0.949 5。而采用改进的遗传-大规模邻域算法求解，使配送成本减少了13.89%，客户满意度提高了3.53%。图5给出了两算法总目标函数值的迭代图，可以看出，本研究设计的改进算法，避免了陷入局部最优现象，能更全面更深入寻找最优解，而且在保证全局最优同时，加速了收敛速度。

图5 总目标函数对比迭代图Fig.5 Total objective function contrastiteration diagram

4 参数敏感性分析

表7 不同下的优化结果Table 7 Optimization result of different

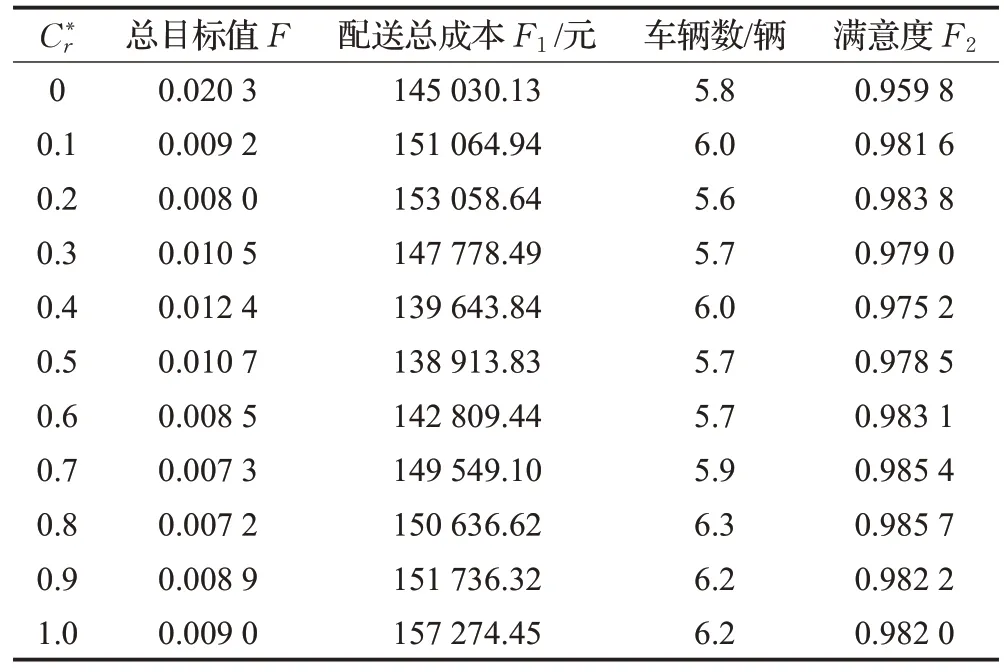
表7 不同下的优化结果Table 7 Optimization result of different

表8 在0.5～0.6之间的优化结果Table 8 optimization result between 0.5 and 0.6

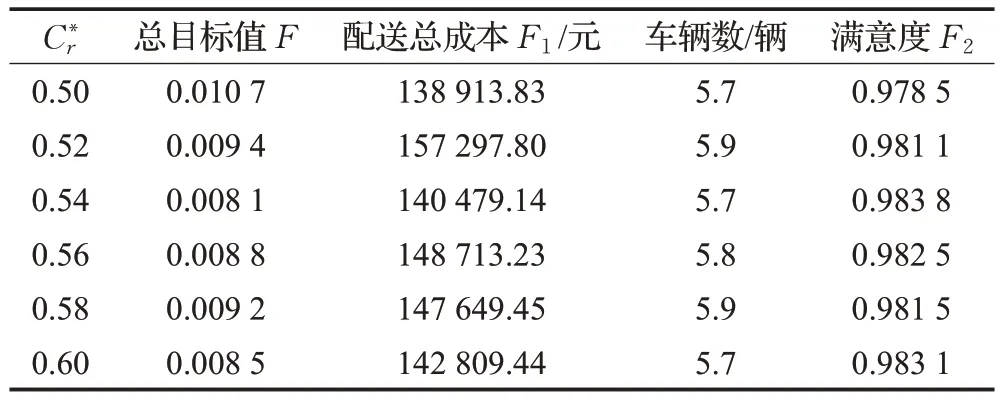
表8 在0.5～0.6之间的优化结果Table 8 optimization result between 0.5 and 0.6

（2）漏热系数β的大小影响着成本函数，以上述冷链物流的MDVRPTWFD 算例中参数β=0.25 为基础，且在其他参数条件不变情况下，上下波动5%、10%，运行10次取平均值，见表9。

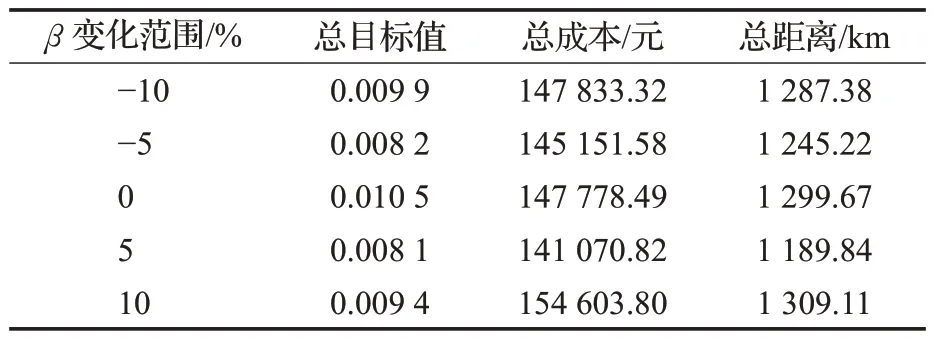
表9 漏热系数β 对各目标值的影响Table 9 Effect of heat leakage coefficient β on each target value

从表9 可知，漏热系数的增大，相应的总成本增大或减少，因为总成本中的制冷成本影响因素不仅仅只考虑漏热，相应运输时间、附加热负荷等都是要根据路径变化所考虑的。所以选择合适的漏热系数对冷链物流路径规划是有必要的。

5 结束语

本研究针对冷链物流配送情况下，对MDVRPTWFD问题进行研究，并设计了改进遗传算法-大邻域搜索算法求解，通过算法对比和算例分析来验证其有效性。结果表明：（1）考虑到冷链配送的特殊性，在配送成本分析方面考虑得很全面，并引入当下倡导的碳排放成本，为冷链物流路径规划研究提供了新思路。（2）冷链物流配送过程中采用多配送中心模式，在保证客户高满意度的同时，减少了车辆的无效调度，降低了配送成本。（3）模型参数影响着优化结果，尤其在考虑需求不确定时，讨论决策者的主观偏好值是十分有必要的。（4）本文设计的改进遗传算法-大邻域搜索算法具有良好的寻优能力，加速了收敛，寻优速度快。

未来将进一步把不断变化的交通情况所引起的时变车速考虑进去，车速的变化会导致到达时间和油耗的改变，进而引起配送成本变化，使研究更贴近实际。