用于UAV运动目标搜索的自适应粒子群算法

杨鸿光，张宇辉，魏文红

东莞理工学院 计算机科学与技术学院，广东 东莞 523808

近年来，无人机（unmanned aerial vehicle，UAV）的低成本、便携性等特性使得其在摄影、勘探、巡检等许多场景中有着广泛应用，特别是在搜索和救援这些寻找动态目标的任务[1]。值得注意的是，在事故发生后的最初72小时内是搜索救援的“黄金时间”，在这期间找到目标的概率是最大的，是营救目标最关键的时间，在这之后的概率会由于各种因素而变得越来越小[2]。因此，无人机路径规划在搜索运动目标的任务中至关重要。找到一条最大化检测概率的无人机路径，有助于提升目标搜寻任务的成功率。

许多元启发式算法由于其可以有效解决动态约束问题，能够在复杂场景中找到全局最优解的能力，而被广泛应用于路径规划中。这些启发式算法可以有效地对动态目标进行路径规划，例如粒子群优化算法（particle swarm optimization，PSO）[3]、人工蜂群算法（artificial bee colony，ABC）[4]、蚁群算法（ant colony optimization，ACO）[5]、遗传算法（genetic algorithm，GA）[6]、差分进化算法（differential evolution，DE）[7]、树种算法（tree-seed algorithm，TSA）[8]、鲸鱼优化算法（whale optimization algorithm，WOA）[9]，和其他可用于路径规划的新型智能优化算法[10]。其中，由于PSO 算法十分简单有效，并且计算量小，得到了广泛使用，并涌现出了许多改进措施。

PSO算法[3]是由Eberhart和Kennedy于1995年提出的全局随机搜索算法，是进化计算的一个重要分支。PSO 模拟自然界鸟类活动，具有“自我认知”和“全局认知”两个群体智能特性。自我认知表示粒子自身经验的影响，全局认知表示粒子之间的信息共享与协作，从而各个粒子能利用个体认知和社会引导来搜索到全局最优解。同时，PSO 对初始条件和目标函数都不太敏感，仅通过一个惯性权重和两个加速因子就能适用于各种环境，在较短的计算时间内找到能稳定收敛的全局解。简单高效的PSO 使其被广泛应用于无人机路径规划中，并产生了基于编码方式的改进，基于参数的改进，基于变异机制的改进，混合其他算法的改进等多种变体[11]，如经典粒子群算法[3]、运动编码粒子群算法（motionencoded PSO，MPSO）[12]、角度编码粒子群算法（phase angle-encoded PSO，θ-PSO）[13]、量子行为粒子群算法（quantum-behaved PSO，QPSO）[14]。PSO 将无人机搜索路径编码为笛卡尔空间的一组节点；MPSO采用包含大小和方向的运动段代替节点，将搜索路径表示为一组运动段；θ-PSO用代表路径出现方向的相位角编码粒子位置，将n个节点的搜索路径表示为2n个角度的向量；QPSO 假设粒子具有量子行为，对粒子的编码方式与PSO 类同，即其搜索路径也是一组坐标节点。其中，MPSO 和θ-PSO 的更新方程与PSO 类似，但QPSO 采用了一个新的随机更新方程。这些变体对粒子编码的形式不一，故在相同的约束及目标函数下可能会产生不同的解。在不同的场景中比较这些变体哪些更加适应于无人机的路径规划，能产生更大概率的运动目标搜索路径，具有重要的研究意义。

已有的文献结果表明MPSO 在各种搜索场景中性能卓越[12]，但有时候MPSO会被两个不同概率的区域混淆，不能识别到概率最大的正确目标区域。θ-PSO 与MPSO面临着相同的困境。PSO无法保持粒子动量，故不能很好地应用于路径规划中。QPSO 在实际应用中不可避免地会陷入局部最优[15]。

受MPSO 算法思想的启发，本文针对MPSO 算法进行了改进，提出了带有自适应学习策略的运动编码粒子群算法（motion-coded PSO with adaptive learning strategy，MPSO-ALS），在保证识别到概率最大的目标区域，不被较低概率目标区域吸引的前提下，获得更大搜索概率的路径，提升性能。本文的主要贡献如下：（1）设计了新的初始化方法，从而确保能识别到概率较高的正确目标区域；（2）融合了子群动态划分策略和自适应学习策略，在保证收敛速度的同时，收敛到概率更高的路径；（3）改进了针对不同类型粒子的更新方程，更好地适应路径规划中子群粒子的学习策略，提高搜索概率。

1 目标函数

本章主要介绍目标函数。目标函数通过对目标、传感器和信念图建模来表示[12]，具体内容如下。

1.1 目标模型

在搜索问题中，由未知变量x∈X来描述目标位置，基于可用信息（目标丢失信号前的最后已知位置）采用概率分布函数对目标位置进行建模，概率分布采用以最后已知位置为中心的正态分布。由网格图形式的信念图b(x0)来表示概率分布图，信念图中的每个单元格的值与目标在该单元格中的概率一一对应。最后将搜索空间S离散化，划分成由Sr×SC个单元格组成的网格，并将目标在该单元格的概率与每个单元格相关联，即可创建搜索图。对于目标所在的搜索图，有

在搜索过程中，目标以一定的模式移动，以马尔科夫过程来对该随机过程建模，在条件确定性目标的特殊情况下，该模式仅取决于目标的初始位置x0。在这种情况下，表示目标从单元格xt-1到xt的概率由转移函数p(xt|xt-1)表示，该转移函数对于所有单元格xt∈S都是已知的。因此，如果目标的初始位置已知，则该目标的移动路径就将完全已知。

1.2 传感器模型

通过在无人机上安装传感器，可以寻找和发现目标。在每个时间步长t进行一次观测zt，每次观测互不影响。每次观察只有两个结果，检测到目标zt=Dt，或未检测到目标，Dt表示在时刻t的检测事件。但由于传感器和检测算法的不完善性，观测到目标zt=Dt并不能确保目标一定存在于xt处。给定传感器模型知识，目标存在于xt处的可能性可由观测概率p(Zt|Xt)反映出来。故在给定目标位置xt的情况下，未检测到目标的概率由公式（1）所示：

1.3 信念图更新

当初始分布b(x0)初始化后，传感器就能够基于贝叶斯方法和观察序列z1:t={z1,z2,…,zt}，产生目标在t时的信念图b(xt)。这通过预测和更新两个阶段递归进行。

预测时，信念图根据目标运动模型随时间传播。假设之前的信念图b(xt-1)在t时可用，则预测信念图可由公式（2）计算：

其中，信念图b(xt-1)实际上是目标在从时间1 观察到t-1时，目标在xt-1的条件概率，即b(xt-1)=p(xt-1|z1:t-1)。

对信念图的更新，只需当观测值zt可用时，将预测的信念图乘以新的条件观测概率即可，更新信念图可由公式（3）计算：

其中，ηt是归一化因子，将目标出现在搜索区域内的概率缩放为1，即，ηt由公式（4）表示：

1.4 搜索问题的目标函数

根据贝叶斯理论，目标在t时未被检测到的概率取决于两个因素：（1）公式（2）得到的最新预测信念图；（2）公式（1）得到的目标未被检测到的概率。针对整个搜索区域，该概率可由公式（5）表示：

由公式（5）可知，rt是公式（4）归一化因子的倒数，即rt=1/ηt（对于未被检测到的事件，），故rt小于1。

通过将未被检测到的概率rt随时间相乘，可以得到从时间1到t时未能检测到目标的联合概率该概率如公式（6）所示：

由公式（5）和公式（6）可得目标在t时第一次被检测到的概率，如公式（7）所示：

对公式（7）中的pt随时间t求和，可得到在时间1到t检测到目标的累积概率，如公式（8）所示：

值得注意的是，累积概率和公式（6）从时间1到t时未能检测到目标的联合概率Rt有如下公式（9）的关系：

同时，随着时间t增加，由于在之前的搜索步骤中检测到目标的机会增大了，故第一次检测到目标的概率pt会变小。由此可得累积概率Pt有界，并且随时间t趋于无穷时向1增加。

综上，搜索问题的目标函数可以由给定有限搜索时间的公式（8）或公式（9）的累积概率Pt表示。假设搜索时间为{1,2,…,N}，搜索策略的目标是确定一条可以最大化累积概率Pt的搜索路径O=(o1,o2,…,oN)，则目标函数可由公式（10）表示：

2 算法背景

本章主要介绍PSO和MPSO的主要步骤，具体内容如下。

2.1 粒子群算法

PSO 算法[3]是一种基于群体智能的随机优化方法。在PSO 中，粒子群模拟鸟群行为在搜索空间中探索（全局搜索）和开发（局部搜索），最终找到全局最优解。粒子的速度和位置更新方程如公式（11）、公式（12）所示：

其中，k表示第k代，lbk是自身历史最优位置，gbk是群体最佳位置，ω是惯性权重，c1和c2分别是个体认知系数和社会引导系数，r1和r2是从[0，1]内采样的两个均匀概率分布的随机序列。

2.2 运动编码粒子群算法

运动编码粒子群算法MPSO[12]保留了PSO的更新机制，但相对于笛卡尔空间，MPSO允许粒子在运动空间中搜索，将粒子移动限制在其相邻单元，从而保证路径中相邻节点之间的距离在无人机移动能力范围内，保持路径节点的可达性，使得每一代进化后的路径总是有效的。

MPSO 将每条搜索路径视为一组无人机运动段，若定义t时某运动段的大小和方向分别为ρt和αt，该运动段则为ut=(ρt,αt)，从而搜索路径为向量集Uk=(uk,1,uk,2,…,uk,N)。使用Uk作为每个粒子的位置，则MPSO的更新方程如公式（13）和公式（14）所示：

其中，ω、c1、c2、r1、r2的作用与PSO 算法中的一致，LBk=(lbk,1,lbk,2,…,lbk,N)和GBk=(gbk,1,gbk,2,…,gbk,N)分别是第k代时某个粒子的自身历史最优和全局最优位置向量集。图1给出了具有三个运动段的路径示例，其中，信念图将概率值用颜色编码并显示在右边。

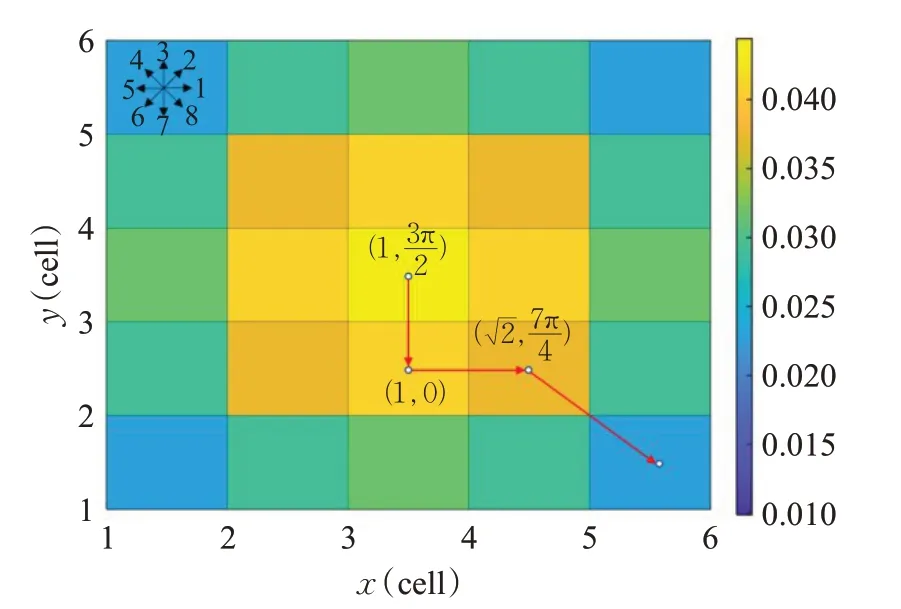
图1 具有三个运动段的运动编码路径Fig.1 Motion coded paths with three motion segments

在搜索过程中，为了评估与路径Uk相关的成本，需要将路径从运动空间映射到笛卡尔空间。如图1所示，映射过程通过将每条无人机路径的每个运动段约束到其8个邻居之一来执行，从而t时的运动幅度ρt可以归一化且运动角度αt可以量化，如公式（15）和公式（16）所示：

通过公式（16）可以得到相对应于运动空间坐标的笛卡尔空间坐标，如公式（17）所示，

3 带有自适应学习策略的运动编码粒子群算法

本章详细介绍所提出的MPSO-ALS 算法。如图2所示，该算法首先通过初始化方案生成原始粒子后，然后根据粒子分布进行子群体动态划分，接着在每个子群中采用普通粒子学习策略和局部最优粒子学习策略指导不同类型粒子的搜索方向，同时进行参数自适应控制。在代数1（a），算法首先通过初始化机制生成随机分散在搜索空间的原始粒子，随后根据粒子的分布找到几个中心粒子作为聚类中心，并划分子群，如代数1（b）。接着，在每次迭代中，将每个子群中的中心粒子当作局部最优粒子，子群中的其他粒子作为普通粒子，每个子群的普通粒子向着该子群的普通粒子引导方向移动，从而增加整个种群的多样性；子群中的局部最优粒子向着局部最优粒子引导方向移动，使得局部最优粒子学习了子群间一些最优粒子的信息，在增加种群多样性的同时，引导该子群收敛到真正的全局最优位置；另一方面，在每次迭代中还要进行参数的自适应控制，如代数i。粒子群在子群动态划分，参数自适应控制，不同类型粒子迭代更新三种方案下持续迭代，不断向着全局最优方向收敛，如代数j。直到满足收敛条件，找到全局最优位置，即概率较高的正确搜索路径，如代数G。

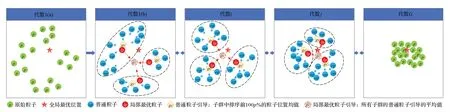
图2 MPSO-ALS算法主要过程图Fig.2 MPSO-ALS algorithm main process diagram

3.1 初始化

在有多个不同概率目标区域的情况下初始化路径时，为了避免粒子因在搜索空间任意方向随意运动，而导致其向较低概率区域探索开发，最终收敛到低概率区域（局部最优），故重新规划了初始化方法。

图3给出了某次初始化路径示例，由图可知，初始化路径位置时，将搜索空间分为8个区域，每个粒子随机在某个区域生成一条向外延伸的路径（超出搜索空间则将路径限制在搜索空间内），这些路径就能覆盖或尽量接近目标的移动路径和最终位置，从而粒子能根据目标函数向较高概率的正确目标区域探索开发，最终收敛到全局最优。同时，为了保持良好的种群多样性，每个粒子都有较小概率ri生成每个运动段方向任意的随机路径。

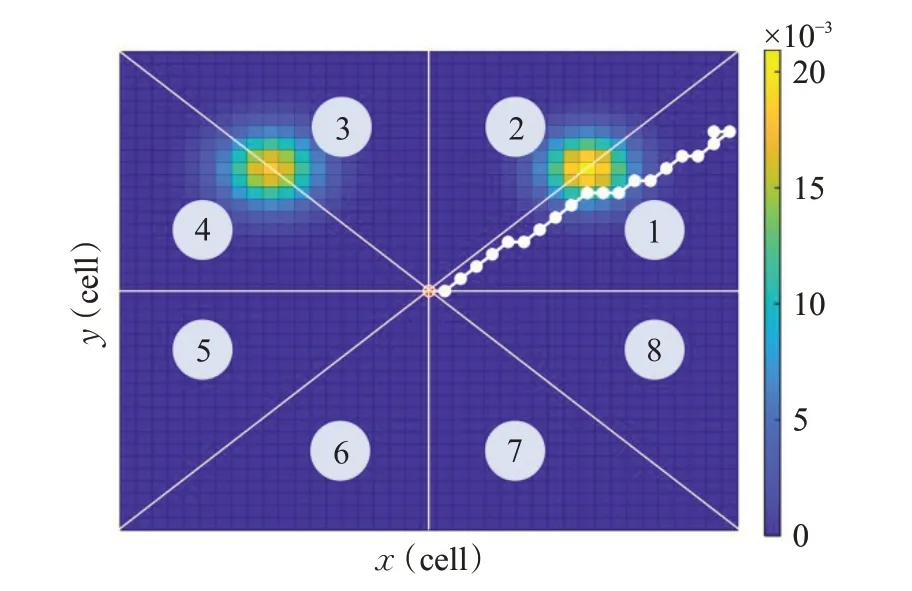
图3 八个方向之一的初始化路径Fig.3 Initialization path in one of eight directions

粒子初始化的质量对粒子群算法的性能至关重要。若粒子搜索路径的运动段数目为N，粒子第一次可以运动到其相邻的8 个网格之一，之后每次运动都只能运动到相邻的7 个网格之一（即不退回前一个位置），则粒子总共有8+7N-1条运动路径，这在运动段数多（问题维数多），且相对运动段而言种群规模不够大的情况下，难以均匀初始化。新型初始化方法基于伪随机初始化方法改进，相对于混沌初始化、均匀初始化、反向学习初始化等其他初始化方法[16]，仅需添加一些限制与随机因子，就能有效地应用于该问题中，获得良好的效果。与传统的伪随机初始化方法相比，该方法生成的种群在搜索空间内是较为均匀且有效的，一般不会集中在低概率区域，导致收敛到局部最优。与混沌初始化策略相比，该方法不太会被问题维度限制，无需设置初值和其他参数，也不会因为吸引子的存在而影响算法效果。由于有8+7N-1种可能的结果，并且粒子是以搜索路径的形式产生，均匀初始化方法[17]较难实现。较之反向学习初始化方案，不用消耗额外的评估次数。相比于准随机序列方法，也不用引入数值算法用以度量差异。总结而言，与其他的初始化方案相比，该初始化方法实现简单，在不引入其他开销与负担的情况下达到良好的效果。

3.2 子群动态划分

子群可以保持种群多样性，避免过早收敛。通过文献[18]中的高性能聚类方法，可以给粒子群的学习策略提供更精确的基础。该聚类方法能自动找到聚类中心，并且可以对任意形状的数据集进行有效聚类，从而提高子群划分的适应性。

聚类算法首先要确定一个好的聚类中心，该聚类中心要满足两点：（1）中心粒子本身的局部密度大，即中心粒子应被局部密度较低的邻居包围；（2）与其他局部密度较高的粒子相距较远。为此给每个粒子定义了两个量：局部密度ρi和距离偏量δi。

局部密度ρi表示粒子i一定距离内的粒子个数，采用高斯核函数来定义，如公式（18）所示：

粒子的位置可以取其在笛卡尔空间的路径中各坐标的均值，dij表示粒子i和粒子j之间的欧氏距离，dc是截断距离，是预先设定的一个值，可以取所有粒子间的距离升序排序后第2%位置的距离值，I是所有粒子的集合。

距离偏量δi是粒子i与其他密度大于该粒子的粒子间的最小距离，对于密度最高的粒子，将其距离偏量设置为所有距离中的最大值，该值本身并无意义，但可让密度最大的粒子的距离偏量也为最大，从而被选为中心粒子之一，距离偏量δi如公式（19）所示：

对于局部密度ρi相同的粒子，可以所有ρi进行降序排序，使得ρi相同的粒子也有先后顺序，从而计算相应的距离偏量δi。

基于公式（18）和公式（19），就可以将具有高ρi和相对高δi的粒子选为中心粒子，如公式（20）所示：

其中，在计算γi时，为避免ρi值和δi值处于不同数量级而出现偏重，可对其进行归一化处理后再计算γi值。

确定所有子群的中心粒子后，就可以一次将其余每个粒子都分配到与之距离偏量δi最小的更高密度的邻居的相同子群中。该一次分配的方法与迭代优化的方法相比，提高了子群划分的效率。另外，区别于传统的基于噪声信号截止的分配方法，该方法引入了一个边界区域，防止低密度子群被归类为噪声。子群的边界区域由这样的一组粒子构成，在它们的距离为截至距离dc的领域内，存在其他子群的粒子。对每个子群，令ρˉ=(ρi+ρj)/2，i指本子群的点，j是与i的距离不超过dc的其他子群的点，计算所有这样的跨子群的粒子对的平均局部密度，取其最大值作为该子群的ρˉ上界，从而子群中密度高于ρˉ的粒子被认为在该子群中，而其余粒子则标记为噪声子群，每个噪声子群都由一个粒子构成。子群划分过程如图4所示。

图4 子群划分过程流程图Fig.4 Flow chart of subswarm division process

3.3 粒子的学习策略

在每个子群中，有两类粒子：（1）子群中的最好粒子，称为局部最优粒子；（2）剩余的粒子，称为普通粒子。MPSO-ALS 使用基于文献[19]改进的不同的学习策略对两类粒子进行更新，以保持种群多样性，避免陷入局部最优。

3.3.1 普通粒子的学习策略

子群中的普通粒子负责利用搜索空间来增强种群多样性，其位置更新方程同公式（14）一致，速度更新方程如公式（21）所示：

其中，ω、c1、c2、r1、r2的作用与MPSO 算法中的一致，LBk=(lbk,1,lbk,2,…,lbk,N)是第k代时某个粒子的自身历史最优向量集，普通粒子引导是第k代时子群c中目标函数适应度值排序前100p%（p∈(0,1]，是给定的比例）的粒子的自身历史最优向量集均值，若某子群的粒子数少于100p%，则取其所有粒子的均值。需要注意的是，普通粒子有微小概率rm突变，重新初始化。

传统的粒子更新方式是所有粒子都基于相同的全局最优粒子来迭代更新，这样仅使用全局最优粒子的搜索信息容易失去多样性，从而陷入局部最优，故在公式（24）中采用了子群中前100p%的粒子信息来更新同一子群中的其他普通粒子，使用粒子能学习到多样化的搜索信息，并有微小概率突变后重新初始化，增加种群多样性。

3.3.2 局部最优粒子的学习策略

子群中的局部最优粒子负责引导普通粒子的学习，并探索其他子群的信息以进一步增加种群多样性，其位置更新方程同公式（14）一致，速度更新方程如公式（22）所示：

其中，ω、c1、c2、r1、r2、LBk、的作用与普通粒子中的一致，C是子群的数量。

对比公式（21）和公式（22）可知，局部最优粒子引导是各子群中普通粒子引导的平均值，这对进一步增大种群多样性，并加快收敛速度十分重要。首先，局部最优粒子引导增加了子群间的信息交流，使局部最优粒子可以学习到更多的路径信息，从而可以增强种群多样性，避免陷入局部最优。其次，局部最优粒子引导考虑了适应值最优的一些粒子的平均信息，这在加快收敛速度的同时，为找到真正的全局最优解提供了有力指导。

3.4 参数的自适应控制

参考了文献[20]中的参数自适应方案，计算粒子间的距离评估此时的状态，调整参数，让参数与进化状态相匹配，以提升搜索效率，加快收敛速度，争取收敛到概率更高的路径。通过取粒子在笛卡尔空间的路径中各坐标的均值作为其位置的代表，粒子间的距离也能体现其进化状态。

3.4.1 进化状态评估

首先，计算每个粒子i相对于其余所有粒子的距离的均值，如公式（23）所示：

其中，NP是种群大小。

其次，取di中的最大距离为dmax，最小距离为dmin，用dg表示全局最优粒子的距离，计算进化因子，如公式（24）所示：

由此可以初步知道粒子的状态分布。粒子分布信息如图5 所示，dpi表示除了全局最优的其余每个粒子的平均距离。当dg≈dpi，表示所有粒子的平均距离差不多，种群多样性良好，在刚开始的探索阶段；当dg≪dpi，表示全局最优粒子逐渐被其余粒子包围，处于开发或收敛阶段；当dg≫dpi表示全局最优粒子找到一个适应值更好的位置，远离原来的位置，其他粒子之后会逐渐往这个更好的值收敛，状态改变顺序为S1→S2→S3→S4→S1→…。

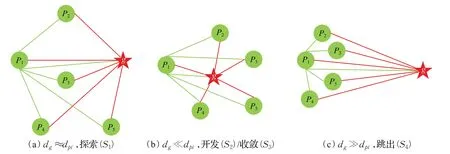
图5 粒子分布信息图Fig.5 Particle distribution information map

最后，采用隶属函数判断此刻的进化状态，四个状态由成员函数μ判断，如公式（25）所示：

从图6 四种进化状态的隶属函数图可以清楚地看出各个状态所属区域，从而根据成员函数值与规则库决定此时的状态。

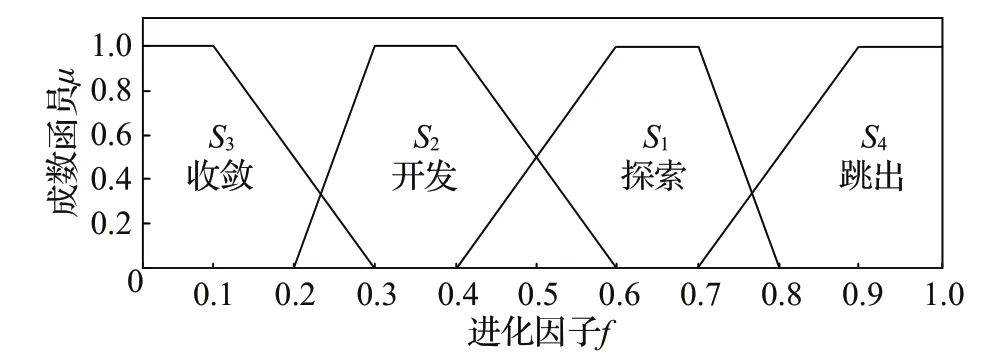
图6 四种进化状态的隶属函数图Fig.6 Graphs of affiliation functions of four evolutionary states

决定粒子所属状态的规则库如表1所示，其中第一行表示当前状态，第一列表示先前状态，一开始的状态为S1。假如当前状态为S1，则判定状态属于S1，如若下一个当前状态为S3&S2，则判定状态属于S2。

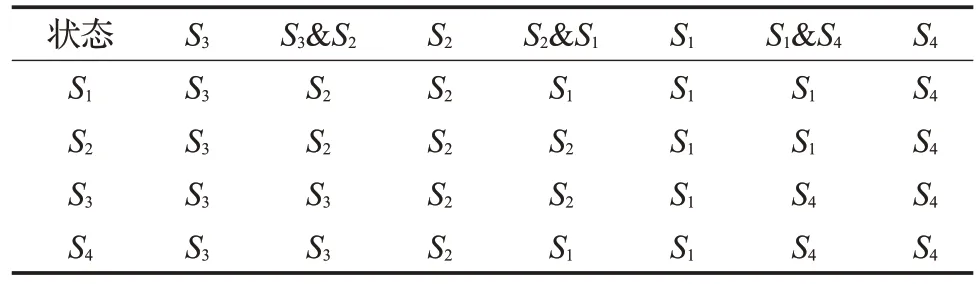
表1 判定状态的规则库Table 1 Rule base for determining status

3.4.2 自适应参数

借助有效的初始化机制，算法可以快速到达收敛状态。由于种群多样性的维持，一开始到达收敛状态后，粒子群还能在探索和开发状态间不断切换，以快速寻找更适宜的路径，此时算法处于全局搜索阶段，惯性权重ω通常较大。粒子群最终会较为稳定地保持在收敛状态，并依旧有一定的种群多样性，有时会转换到其他三个状态，从而不断找到更贴合目标运动路径并最终找到目标的概率更高的搜索路径。此阶段要求粒子群不断减小ω，从而能不断找到更高概率的路径，并最终收敛到概率最高的路径。ω根据进化代数线性递减与问题更为贴合，若采用激活函数，则ω会在到达收敛状态时就保持在一个较小的值，不利于粒子的搜索。故惯性权重ω根据进化代数线性递减即可，g是当前代数，G是总迭代次数。

加速因子c1代表个体认知，促进粒子获得自身最好位置，有利于开发局部最优，增加多样性；c2代表社会认知，推动粒子向全局最优区域收敛，加快收敛速度。故其加速策略如表2所示。

表2 c1 和c2 的控制策略Table 2 Control strategies for c1 and c2

策略1在探索状态增加c1，减小c2：强调个体认知，帮助粒子探索自身最优个体，避免过早聚集，陷入局部最优。

策略2在开发状态轻微增加c1，轻微减小c2：轻微增加c1可以使c1维持在一个较大的值，利用局部信息，在个体最优周围探索和开发；此时全局最优粒子不一定在其真正的最优区域，轻微减小c2可避免算法过早收敛，陷入局部最优。

策略3在收敛状态轻微增加c1，轻微增加c2：此时群体可能已经找到全局最优区域，c1应该减小，同时增加c2才有利于引领其他粒子向可能的全局最优收敛。但经过实验测试，此时减小c1并增加c2会使这两个因子的值过早到达上下边界，可能会使局部最优区域被当成全局最优区域而快速收敛，所以应该对c1和c2都轻微增加。

策略4在跳出状态减小c1，增加c2：使全局最优粒子获得更好的值，跳出当前最优，离开原来的聚类而迈向更优的区域。

为了使c1和c2每一代平稳变化，不过于突兀，c1和c2增加与减小的值从加速率ϕ=[0.01,0.05]间隔中随机产生，而策略2和策略3中的轻微改变从0.5ϕ中随机产生。需要注意的是，如果c1和c2的和超过了5.0（c1和c2的初始值为2.5），要对之进行归一化处理，限制在边界内，即

在策略3 的收敛状态时，对于最优粒子，随机对其某一个维度加入高斯扰动，令其获得跳出当前最优位置，离开当前聚类，得到更好的值的能力。只选择一个维度是因为当前最优可能具有全局最优的一些良好结构，故应保护好它。具体如公式（26）所示：

图7 展示了优化过程中加速因子c1和c2的自适应变化情况，结果取自10次运行的平均值。可以看出，在初始探索、开发阶段，粒子利用局部信息，在个体最优周围探索和开发，c1数值增加。同时，控制策略为了避免收敛到局部最优，出现无法很好地跟踪目标的运动路径，目标函数评估值较小的情况，减小了c2。随着群体达到收敛状态，粒子群已经找到了能够较好地跟踪并找到运动目标的路径，应引领其他粒子向可能的全局最优搜索路径收敛，c1和c2方向反转，c1减小而c2增加。由于子群体多样性的维持，粒子有时会转换到其他三个状态，故有时出现c1突然增加而c2减小的情况。最终，粒子群对全局最优搜索路径不断细化，提高目标函数评估值，所以c1和c2回到初始值2.5附近。加速因子c1和c2平均值的变化表明，进化状态评估确实能够识别粒子群的进化状态，并进行参数自适应控制来提高算法性能。相对于标准PSO，参数自适应控制加快了收敛速度，弥补了子群体维护带来的收敛速度较慢的缺陷，使其能够细化解，提高所找到的路径的搜索成功概率。参数自适应流程图如图8所示。

图7 加速因子c1 和c2 的平均值Fig.7 Average of acceleration factors c1 and c2

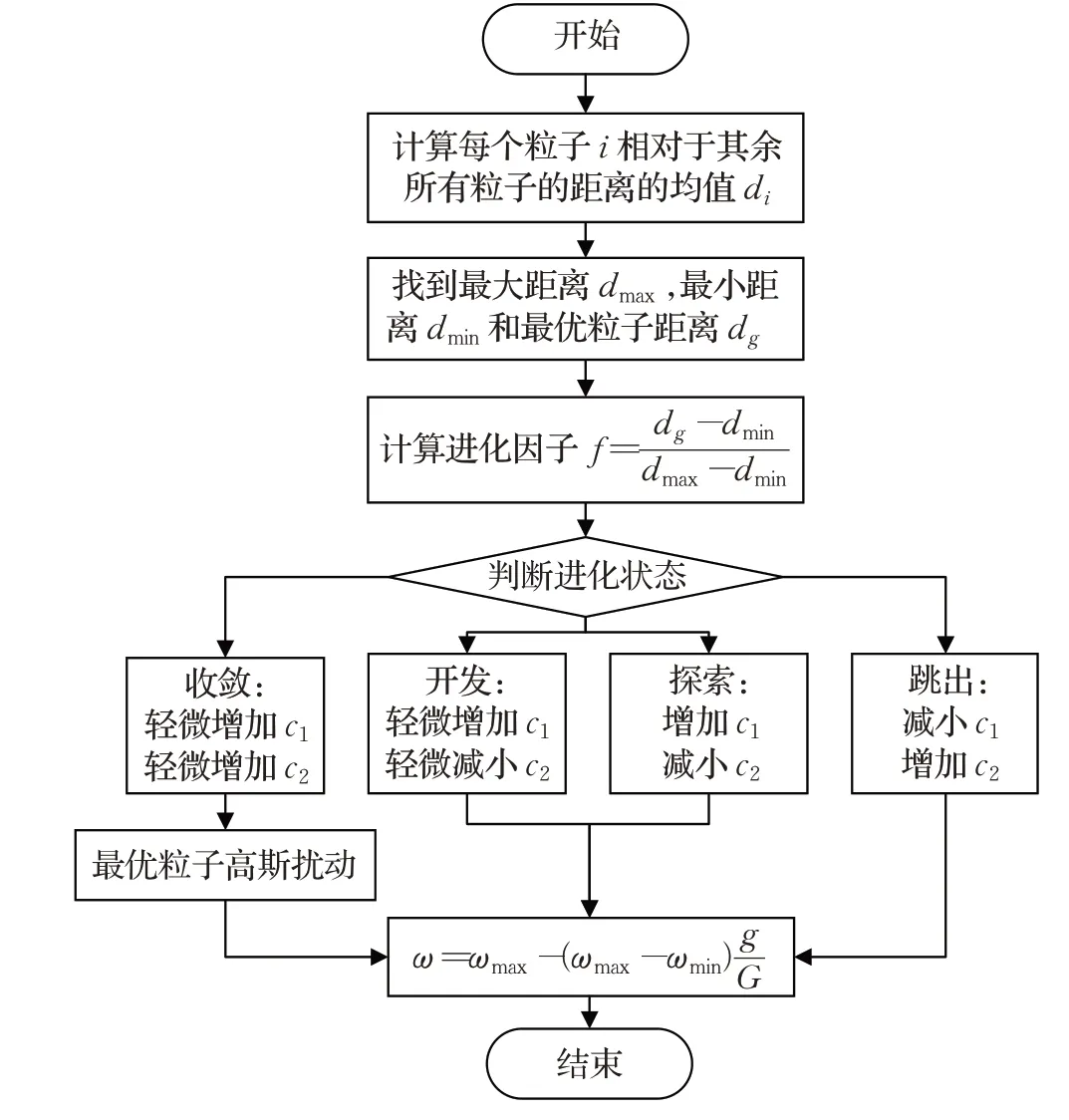
图8 参数自适应控制流程图Fig.8 Parameter adaptive control flow chart

3.5 算法分析

带有自适应学习策略的运动编码粒子群算法的流程图如图9 所示。其中，新的初始化机制相对于混沌化、均匀化等初始化策略，实现简便，可以在不引入其他开销的情况下，保证粒子识别到概率最高的正确目标区域，避免粒子陷入局部最优。另外，结合粒子群动态划分机制，改进了不同类型粒子的更新方程以适应子群策略。其中，普通粒子由子群c中目标函数适应度值排序前100p%的粒子的自身历史最优向量集均值代替全局最优粒子作为社会引导，从而使粒子可以学习到搜索空间中多样化的搜索信息，保持各子群的种群多样性，避免陷入局部最优；局部最优粒子由各子群中普通粒子引导的平均值代替全局最优粒子作为社会引导，使该粒子可以学习到子群间最优的一些路径的平均信息，从而局部最优粒子在保持多样性的同时，能有效指导普通粒子的学习，找到真正的全局最优解。不同类型粒子的学习策略在保持种群多样性的同时很好地提高了搜索概率。最后，根据进化状态进行相应的参数ω、c1和c2自适应控制[20]，加快收敛速度以弥补划分子群所导致的收敛速度较慢的缺陷，提高算法的运动目标搜索成功率。另一方面，子群划分引入了局部密度ρi和距离偏量δi，参数自适应引入了加速率ϕ和高斯扰动标准差σ，这些参数求解或设置简单，可以在不引入巨大负担的情况下提升搜索性能。

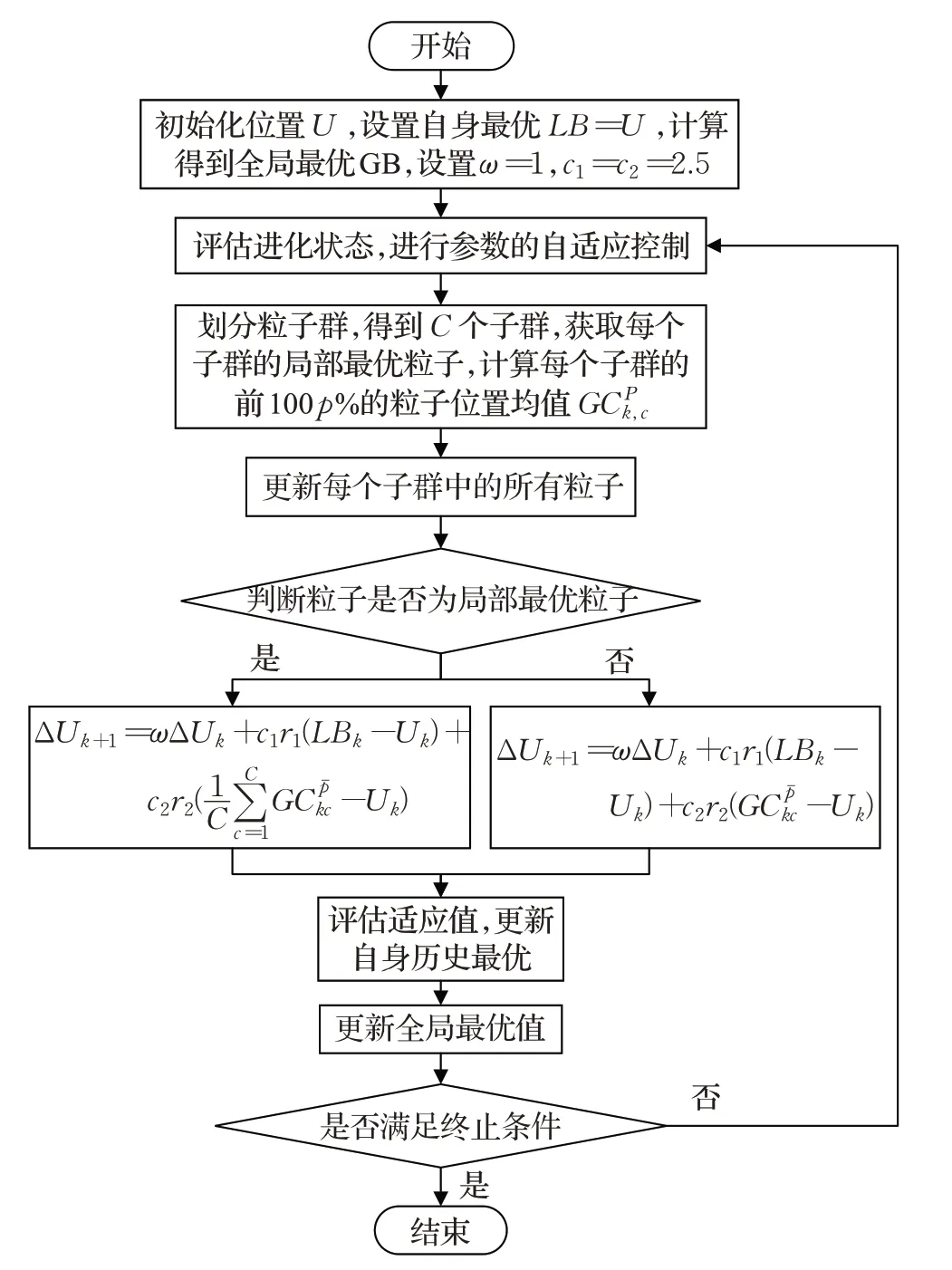
图9 MPSO-ALS流程图Fig.9 MPSO-ALS flow chart

4 实验分析

本章分析MPSO-ALS 的复杂度和种群多样性，并通过与其他启发式算法进行实验对比，评估MPSO-ALS的性能。

4.1 复杂度分析

标准PSO 算法的时间复杂度主要由粒子初始化(Tini)，基于学习策略的更新(Tupd)和成本评估(Teva)三部分构成。设种群规模为p，问题维度为d，最大适应度评估次数为m，则标准PSO 算法的时间复杂度为T(d)=Tini+(Tupd+Teva)m=pd+(2pd+pd)m=pd(3m+1)，即O(pdm)。

相对的，MPSO-ALS算法的时间复杂度主要由粒子初始化(Tini)，计算粒子位置(Tcp)，子群动态划分(Tsdd)，普通粒子和局部最优粒子基于学习策略的更新（Tupd-op和Tupd-lbp），进化状态评估(Tese) 和成本评估(Teva) 组成。其中Tsdd包括距离矩阵计算(Tdis)，局部密度ρ计算(Tρ)，距离偏量δ计算(Tδ) 和划分子群(Tds) 四部分。算法各部分所需花费的计算时间如下，粒子位置需要计算其在笛卡尔空间的路径中各坐标的均值，即Tcp=p；由粒子位置可计算每两个粒子之间的距离得到距离矩阵，即Tdis=p2d；由距离矩阵计算每个粒子的局部密度，即Tρ=p2；由局部密度计算每个粒子的距离偏量，即Tδ=p2；由局部密度和距离偏量进行子群划分，即Tds=p；粒子更新需要获得适应度值排序前几名的粒子的自身历史最优向量集均值来引导更新，则Tupd-op=Tupd-lbp=p+2pd；进化状态评估主要计算每个粒子相对于其余所有粒子的距离的均值，具体只要在粒子的距离矩阵上进行求和及平均，即Tese=p2。故T(d)=Tini+[Tcp+(Tdis+Tρ+Tδ+Tds)+(Tupd-op+Tupd-lbp)+Tese+Teva]m=pd+[p+(p2d+p2+p2+p)+2(p+2pd)+p2+pd]m=pd+(p2d+3p2+5pd+4p)m，即MPSO-ALS 的时间复杂度为O(p2dm)。

4.2 种群多样性分析

MPSO-ALS 部分典型迭代时刻的个体分布图如图10所示，图中白色圆圈表示无人机初始位置；红色、绿色和青蓝色粒子表示三个粒子子群，粒子位置取其在笛卡尔空间的路径中各坐标的均值；三个白色星号表示各个子群中的局部最优粒子搜索路径的最终位置；采用颜色编码的信念图是更新后的信念图，表示目标最终运动到位置（10，10）附近，并且在（10，10）位置的可能性最大。

图10 MPSO-ALS典型迭代时刻的个体分布图Fig.10 Distribution of individuals at typical iteration moment of MPSO-ALS

代数1 为初始化后的粒子，从图10（a）可以看到粒子分布在初始位置四周，表示粒子群以初始位置为起点不断向四周延伸的状态，从而能尽量接近目标的移动路径和最终位置，确保粒子向高概率的正确目标区域收敛。代数4 时粒子群已经处于收敛状态（图10（b）），某一子群的局部最优粒子已经到了目标位置附近，但其搜索路径不一定很好地跟踪了目标运动，搜索概率并不是很高。由图可知，直到27代前，由于子群动态划分策略和子群中不同粒子的学习策略增加并保持了种群多样性，粒子群不断在探索和开发状态间切换，寻找并跟踪着目标。27代后，粒子才基本保持在收敛状态，并且找到了（10，10）这个可能性最大的位置。之后每一代，粒子群在利用子群策略维持多样性的同时，通过参数自适应控制加快收敛速度，不断迭代，在收敛状态下去寻找概率更高的搜索路径，在70 代时找到了概率较高的搜索路径，到100 代时找到了概率更高的搜索路径。

4.3 实验场景设置

实验采用了文献[12]中的场景设置，使用6 种搜索场景来表示不同的搜索情况，以达到覆盖作用，从而可以很好地分析MPSO-ALS的性能。如图11所示，6个场景的地图大小都为Sr=SC=40，但无人机的初始位置、初始信念图b(x0)和目标运动模型p(xt|xt-1)不同。其中，信念图采用颜色编码，用白色箭头表示目标动态，用白色圆圈表示无人机初始位置。

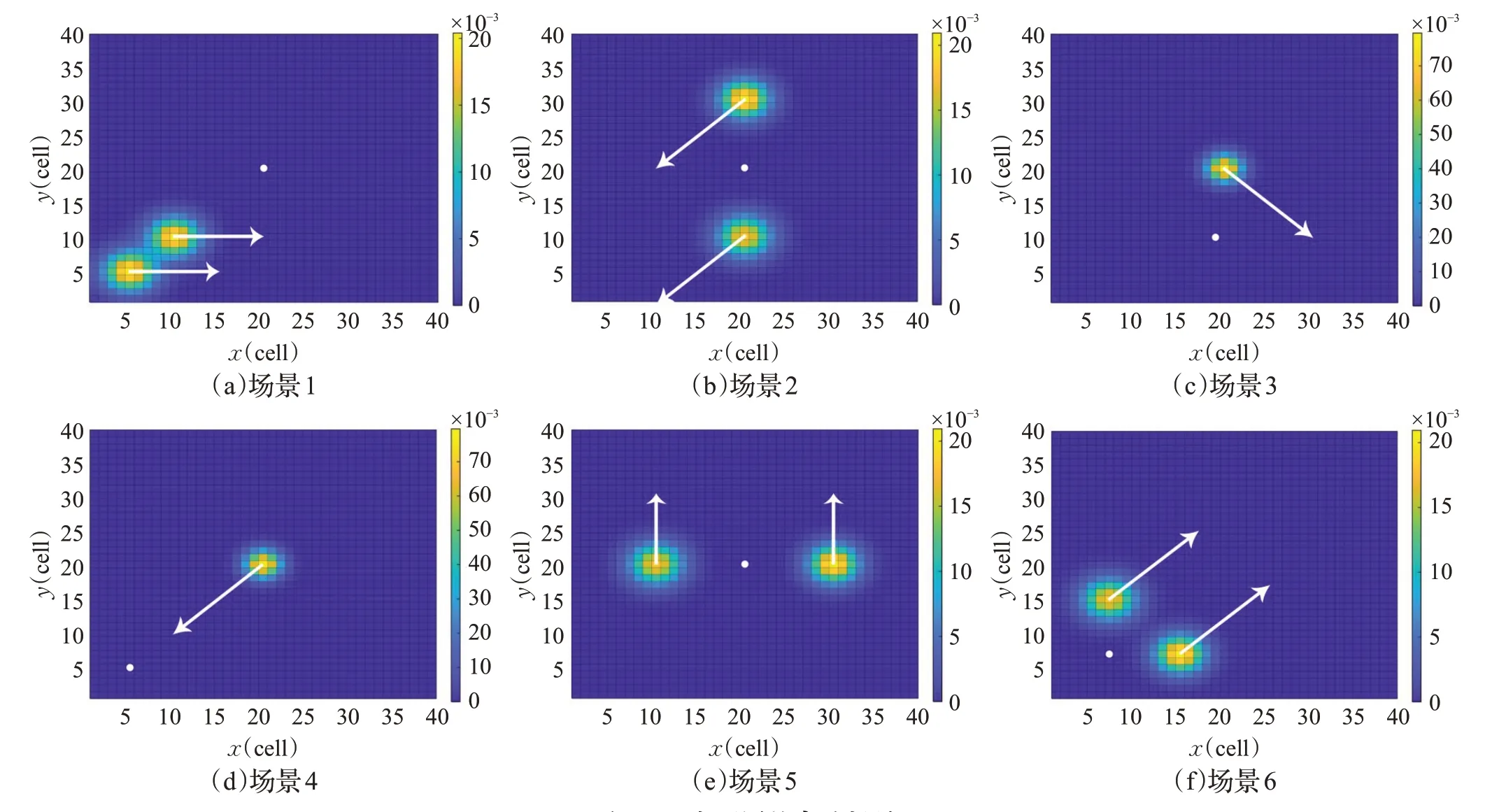
图11 6个不同的实验场景Fig.11 Six different experimental scenarios

场景1：有两个高概率区域，它们彼此相邻并向东移动，但在位置和概率值上略有不同，有一定的混淆作用，可能导致难以找到更好的区域来搜索目标。

场景2：在无人机上下相对位置有两个彼此分离的高概率目标区域，它们向西南方向移动，算法需快速识别要搜索和跟踪的区域。

场景3：有一个小型密集区域向东南方向快速移动，需要算法有良好的探索和适应能力。

场景4：与场景3类似，但目标区域向无人机起始位置移动，进一步测试算法的探索和适应能力。

场景5：在无人机左右相对位置有两个彼此分离的目标区域向北移动，它们与无人机距离时刻相等，但右侧区域的概率较高，算法需识别到正确的高概率目标区域。

场景6：与场景5类似，但无人机位于目前潜在区域的下方，而目标区域向东北方向移动，检验了算法在对角线方向上搜索到正确目标区域的能力。

MPSO-ALS的参数设置如下：惯性权重ω=1，加速因子c1=c2=2.5，子群数c=3，粒子选取比例p=0.003，初始化突变概率ri=0.1，普通粒子突变概率rm=0.001。种群大小为1 000个粒子，迭代次数100次，搜索路径为20个节点。算法独立运行10次以找到每种场景下的均值和标准差。

4.4 搜索路径

图12 是MPSO-ALS 在6 个场景中的搜索路径和累积概率值，其概率图仅反映最后一步的目标信念，而无人机搜索路径则反映了随时间变化的对高概率正确目前区域的跟踪路径。无论在哪个场景中，该算法都能找到概率最高的正确目标区域，并生成能适应目标动态以最大化检测概率的搜索路径。需要注意的是，场景3和场景4中的累积概率值大于其他场景，这是因为这两个场景都只有一个高概率的目标区域，所以找到目标的机会不会扩散到其他混淆区域中。

图12 MPSO-ALS在每个场景的搜索路径和累积概率值Fig.12 MPSO-ALS search paths and cumulative probability values in each scenario

4.5 与其他PSO算法的对比分析

这一部分主要描述PSO 算法相对于其他PSO 变体的优势，这些PSO变体在引言和2.2节都已有描述，其结果从文献[12]中获得。

表3是10次运行后，MPSO-ALS和其他PSO算法在累积检测概率适应值上的平均值和标准差，加粗字体表示其适应值在对比算法中最优。由表可得，MPSO-ALS在所有6 个场景中的性能都是最好的，收敛也较为稳定，这说明初始化方案和自适应学习策略的有效性。例如，在场景1中，MPSO-ALS的适应值是0.204 7，而次优的MPSO 是0.187 6，θ-PSO 是0.186 9，PSO 和QPSO 分别是0.147 6 和0.119 8，故MPSO-ALS 提升了0.017 1 以上。在场景2、3、5、6中也有类似的提升。特别的，在场景4中，MPSO-ALS的0.545 4比次优MPSO的0.501 8提升了0.043 6，这说明对于突然折回探索的场景，MPSOALS 的性能是更优的，即相对于其他PSO 算法，MPSOALS的多样性更好且收敛良好。MPSO和θ-PSO次之，并且结果相近，因为它们的编码方式允许它们在运动空间中搜索。PSO和QPSO适应值最小，这是因为它们所使用的对节点的编码方式无法保持粒子的动量而导致局部最优。

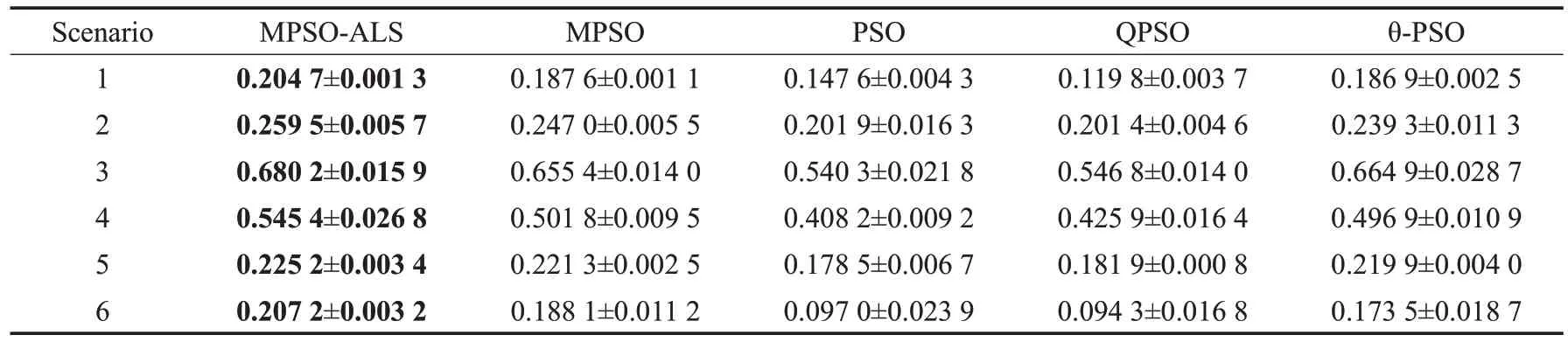
表3 MPSO-ALS和其他PSO变体的适应值比较Table 3 Comparison of MPSO-ALS and other PSO variants with respect to fitness

从图13中10次运行后各类PSO算法的平均适应值收敛曲线图也可知，MPSO-ALS 较之MPSO，在除了场景5 的其他场景中都有明显的性能提升，而场景5 只有微小提升。另一方面，可以注意到在场景1和场景6中，MPSO-ALS 的收敛速度非常快，分别在第9 代和第8 代就超越了次优的MPSO的最终收敛值，并逐渐收敛到更优的路径，说明其不会被其他高概率区域混淆且在对角线方向上的探索开发能力较强，但在其余4个场景中的探索能力则很弱，这可能是子群部分在早期容易被局部最优区域吸引导致。MPSO 性能次之，但在场景2 到场景5 中的探索开发能力强于MPSO-ALS，这些场景中，MPSO-ALS分别需要37代、33代、48代、39代才能超过MPSO 的最终收敛值，且超过MPSO 最终收敛值前的收敛速度基本低于MPSO。θ-PSO 稍弱于MPSO。而PSO和QPSO则很容易陷入局部最优，与其他算法差距较大。

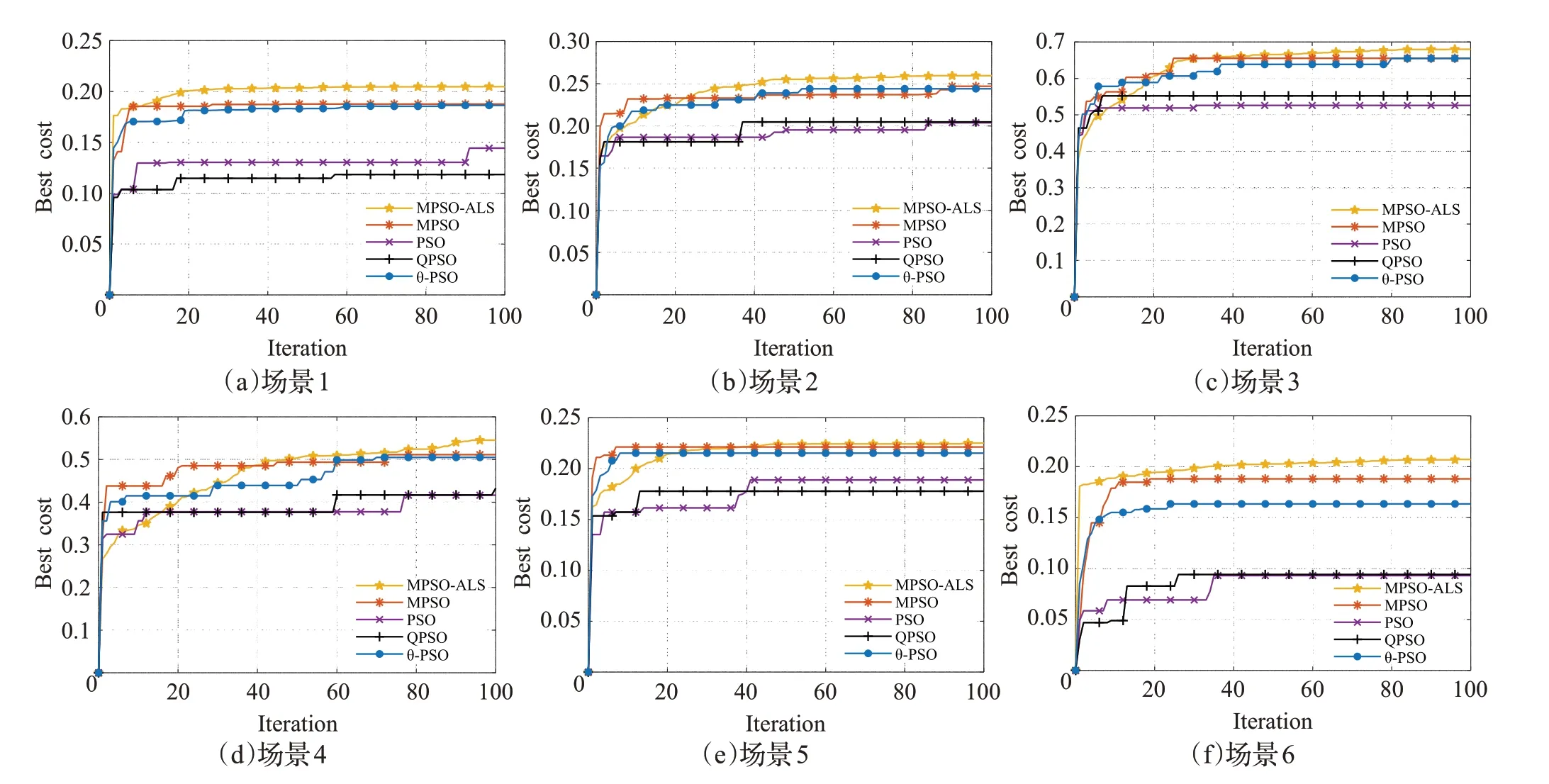
图13 MPSO-ALS和其他PSO变体的收敛曲线图Fig.13 Convergence curves of MPSO-ALS and other PSO variants

4.6 与其他启发式优化算法的对比分析

这部分将MPSO-ALS 与其他元启发式算法进行比较以进一步评估其性能。用于比较的算法是ABC，ACO，GA，DE 和TSA 算法，其结果从文献[12]中获得。ABC 将人工蜂群分为雇佣蜂、观察蜂和侦察蜂三种蜜蜂。在进化过程中，雇佣蜂和观察蜂负责开采过程，而侦察蜂负责随机搜索蜜源，最终将解决方案表示为一组由运动段组成的搜索路径。ACO通过蚂蚁信息素通信来找到从蚁穴到食物源的最短路径，由最大最小蚁群和文献[21]中的“ACO-Node+H”方法实现。GA 模拟物竞天择的自然进化过程，通过个体的选择、交叉和变异获得最优染色体，由文献[22]中的“EA-Dir”方法和两种变异技术“flip”和“pull”实现。DE 通过对种群进行变异、交叉和选择三种操作来获得最优解，是基于种群的群体进化算法。TSA基于树木生长衍化，同时探索和开发并利用树群种子传播解决优化问题。

算法的平均适应值和标准差如表4所示，加粗字体表示其适应值在对比算法中最优，图14 显示了其对应的收敛曲线图。由表4 可知，MPSO-ALS 在6 个场景中都优于其他启发式算法。TSA次优，其适应值与MPSOALS在除了场景5的其他场景中都有明显差距。例如，在场景5中，MPSO-ALS仅仅比TSA的适应值多0.004 3，但在场景1 中却相差0.017 4，场景2、场景6 与场景1 类似。特别的，在场景3 中，MPSO-ALS 的0.680 2 比TSA的0.623 6 高了0.056 6；而在场景4 中，MPSO-ALS 的0.545 4则远高于TSA的0.462 6，相差0.082 8。GA性能最差。

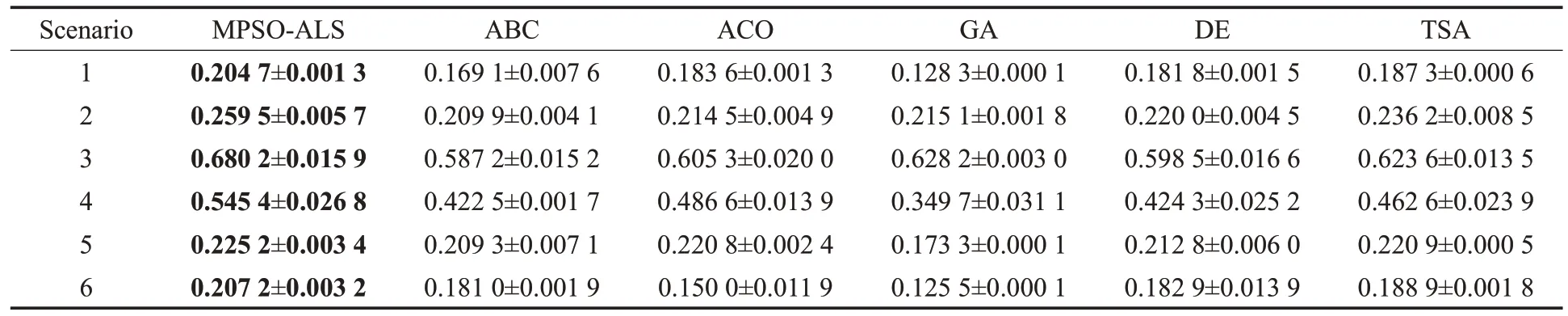
表4 MPSO-ALS和其他启发式算法的适应值比较Table 4 Comparison of MPSO-ALS and other metaheuristic algorithms with respect to fitness

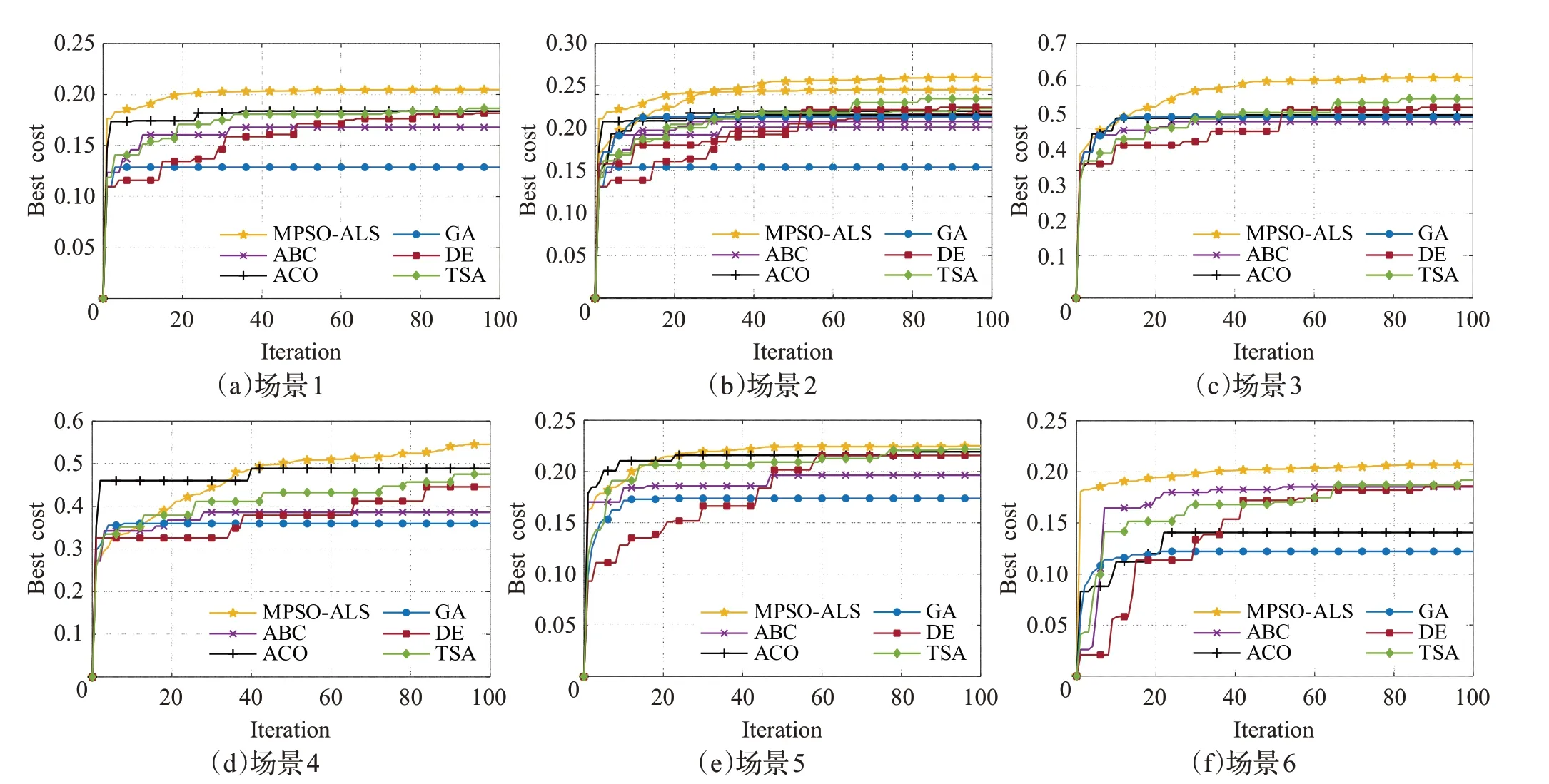
图14 MPSO-ALS和其他启发式算法的收敛曲线图Fig.14 Convergence curves of MPSO-ALS and other metaheuristic algorithms

从图14 可以明显看出各算法间的区别。MPSOALS 以高适应值优于其他算法，但在场景3 和场景4 中的收敛速度明显弱于大部分算法，这表明其在对较小的高概率区域的探索能力的不足。TSA 开发能力有限以至于最终收敛值弱于MPSO-ALS。与最终收敛值基本处于次优的TSA 相比，MPSO-ALS 在场景1 和场景6中分别只用了9 代和11 代就超过了TSA 的最终收敛值。在场景2 到场景5 中则分别需要25 代、24 代、35代、39 代来超过TSA 的最终收敛值。需要注意的是，MPSO-ALS 对场景3 和场景4 中的较小高概率区域的探索能力不足，故在分别到达24 代、35 代前，收敛速度慢于其他对比算法。ABC 和ACO 性能良好。DE 的探索、开发和收敛能力都较弱，很久才达到其收敛值。GA 性能最弱，可能是因为交叉和变异操作会产生许多无效的搜索路径，导致其容易陷入局部最小值。

5 总结

为了提高无人机搜索运动目标的累积检测概率，受MPSO算法思想的启发，提出了带有子群体动态划分策略和自适应学习策略的运动编码粒子群算法MPSOALS。该算法规划了新的初始化机制，使其更容易跳出局部最优。另一方面，改进了不同类型粒子的更新方程，使得算法在采用子群划分来保持多样性的同时，能赋予子群中的普通粒子和局部最优粒子不同的学习策略。最后在迭代过程中对参数进行自适应控制，以加快收敛速度。实验结果表明，MPSO-ALS不会陷入用于混淆的目标区域中，并且在所有搜索场景中的搜索性能都有所提升。在未来的研究中，会专注于提升MPSO-ALS的性能并将其应用到多运动目标搜索领域。