聚焦新课标，研读新教材，践行新理念

包东妹

摘要：以一节公开课为载体，呈现了一位数学教师如何聚焦新课标、研读新教材、践行新理念的生活常态，围绕教学设计中的三个难点“如何有效利用情境抽象数学概念”“如何将琐碎的知识点串成一条线”“如何彰显引言课的作用”进行专项突破.

关键词：新课标；新教材；新理念2022年9月，无锡市高中数学新教材培训活动在太湖高级中学举行，笔者受邀上了一节公开课——数列的概念（第1课时）（人教A版选择性必修二），同课异构的队友是获得全国赛课一等奖的张长贵老师，在经历了备课、磨课、上课，同行切磋与交流后，感触颇深，现将备课中比较纠结的几个难点的突破过程和课堂效果整理成文，以飨读者.

1如何有效利用情境抽象数学概念新课标指出：数学学科核心素养通常是在综合化、复杂化的情境中，通过个体与情境的有效互动生成的，数学教学活动是学生的数学学科核心素养形成和发展的重要途径，在数学教学中需结合教学任务及其蕴含的数学学科核心素养，设计切合学生实际的情境和问题，引导学生用数学的眼光去观察现象、发现问题，使用恰当的数学语言、模型描述问题，用数学的思想、方法解决问题.

教科书给出三个引例：王芳的身高（生活实例）、古代巴比伦泥版上的月相变化（数学文化）、-1/2的n次幂（数学内部），并安排了一个归纳栏目，让学生归纳上述三个例子的共同特征.

第一遍备课，深切领会教材意图，从三个典型情境中抽象数学概念.在此基础上笔者提出自己的不同想法：一是月相变化的例子情境很长，抽象出来的一列数与王芳的身高抽象出来的一列数的意义和用途相近；二是想扩大情境的作用，不仅要利用情境提炼数列的概念，还要对后续研究数列的分类、性质、通项公式等都有启发引导的价值，所以对情境的选择进行了一番考虑，设置如下：

1. 王芳从1岁到9岁的每年生日都会测量身高，将她的身高数据（单位：cm）依次排成一列数：75，87，96，103，110，116，120，128，138.

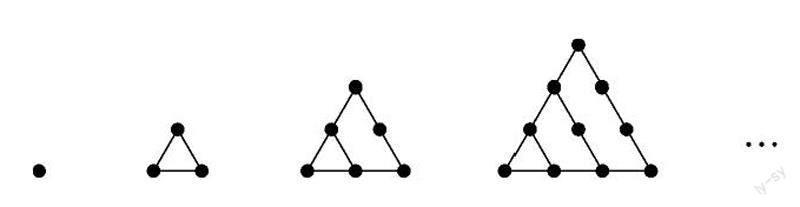
2. 古希腊毕达哥拉斯学派的数学家用沙粒和小石子来研究数，下图中的小石子代表的数依次为：1，3，6，10，…

（设计意图：取代月相变化的例子，从图形中概括数列，既有数学文化的趣味性，也体现情境表达的另一种方式，且此数列蕴含数列前后项之间的联系，为后续学习递推关系埋下伏笔.）

3. 100以内的正偶数按从小到大的顺序依次排成一列数：2，4，6，8，…，100.

4. -1/2的n次幂按1次幂、2次幂、3次幂、4次幂…的顺序依次排成一列数：-1/2，1/4，-1/8，1/16，…

（设计意图：3和4的例子都是从数学内部提出问题，体现项与序号之间的规律性，便于总结通项公式，也表达了单调增数列和摆动数列的变化差异性.）

5. 无穷多个-1排成一列数：-1，-1，-1，-1，…

（设计意图：体会数列中的项可以重复，与集合元素的互异性不同.）

6. 3的不足近似值按小数点后位数从少到多的次序排成一列数：1，1.7，1.73，1.732，1.7320，1.73205，…

（设计意图：让学生感受这个数列后面的项是确定的，只是说不出是多少，项与序号之间确实是一一对应的关系，但不能用通项公式来表示.）

去除情境，剩下六列数，让学生观察这六列数，归纳它们的共同特征.

学生给出的反应是前三列数都是单调递增，第四和第五列又不满足这个规律，立马又否定了自己的发现，单调性不是共同特征.

反思：第一，去掉了情境以后学生理解“有序”是困难的；第二，这六列数放在一起对“有序”的概念不够聚焦，反而更突出了单调性等体现差异性的特征.

第二遍備课，设置如下四个情境：

1. 王芳从1岁到9岁的每年生日都会测量身高，将她的身高数据（单位：cm）依次排成一列数：75，87，96，103，110，116，120，128，138.

2. -1/2的n次幂按1次幂、2次幂、3次幂、4次幂…的顺序依次排成一列数：-1/2，1/4，-1/8，1/16，…

3. 3的不足近似值按小数点后位数从少到多的次序排成一列数：1，1.7，1.73，1.732，1.7320，1.73205，…

4. 100以内的正偶数按从大到小排列的顺序依次排成一列数：100，98，96，…，2.

（设计意图：体现不同排列方法，降低单调递增的认同感.）

【课堂片段一】

问题1：观察上述情境中的四列数，它们有何共同特征？

生1：依次排列.

教师：它们分别是按照怎样的次序排列的呢？

生1：第1列数按年龄从小到大的顺序，第2列数按幂指数从小到大的顺序，第3列数按小数点后位数从少到多的顺序，第4列数按数值从大到小的顺序.

教师：回答得漂亮.

引导学生抽象数列的概念：按照确定的顺序排列的一列数.

紧接着，教师拿出以下两个情境，让学生辨析它们是否是数列.

5. 古希腊毕达哥拉斯学派的数学家用沙粒和小石子来研究数，下图中的小石子代表的数依次为：1，3，6，10，…

6. 无穷多个-1排成一列数：-1，-1，-1，-1，…

【课堂片段二】

教师：情境5中的这列数是不是一个数列？这个省略号蕴含了后面有无数个图，那么第五张图，第六张图分别代表的数是多少？你是怎么发现的？

学生的表现让人惊喜，说出了后一个数与前一个数的关系.

教师：情境6中的这列数是一个数列吗？

生1：不是，因为它没有确定的顺序.

教师：这里每一项是一样的，非常特殊，虽然它可以交换顺序，但是我们也可以认为它是有序排列的.

教师：集合中的数我们把它称之为元素，数列中的每一个数，我们称之为项.请你说说数列中的项与集合中的元素有什么区别？

（设计意图：体会知识之间的联系与区别，增强对数列概念的理解.）

2如何将琐碎的知识点串成一条线新课标指出：数学核心素养的发展具有整体性与阶段性，是学生在数学课程内容的学习过程中逐渐形成的.高中数学课程内容按照函数、几何与代数、概率与统计、数学建模活动与数学探究活动四条主线展开，将数列内容置于函数主题之下，意味着数列是函数内容的重要组成部分，其作为离散型函数，与幂函数、指数函数、对数函数、三角函数一样，都是重要的函数模型.这样设置更加突出了数列的函数本质，强调了数列的基础性，丰富了函数的知识结构，进一步深化了学生对函数的理解，体现了数学知识的整体性、发展性和联系性.

根据新课标和教科书呈现的内容，设定本节课知识层面的教学目标：通过观察情境，学生能够概括出数列的概念，知道项的概念，抽象出数列的一般形式，体会数列的部分性质和分类，归纳出简单数列的通项公式，感受和理解数列是特殊的函数等等.从表面上看，知识点琐碎，前后联系不紧密，对教师来说实践操作也非常困难.笔者思考：如何呈现知识的先后顺序才能做到自然？如何巧妙衔接知识点才能让知识的生成水到渠成，方法的运用润物细无声？

渠东剑老师归纳的函数知识的发展线索（如上图所示）给笔者以很大的启发，数列是特殊的函数，因此我们可以借鉴函数的研究套路来研究数列，这也体现了大单元教学和主题式教学的作用.于是设计了以下四个问题，以问题串的形式将知识点串成了一条线，构成了本节课的一条明线.

问题1：观察上述情境中的四列數，它们有何共同特征？

（设计意图：归纳共性，抽象出数列和项的概念，概括出数列的一般表示形式，并将数列中的项与集合中的元素进行比较，感受数列和集合两者的差异性.）

问题2：观察这六列数，它们有何不同特征？

（设计意图：分析差异，提炼数列的性质——单调性等，并将数列按不同标准进行分类.）

问题3：数列的项与它的序号是否有一定的对应关系？

（设计意图：学生易于从第2、4、6个数列写出项和序号之间的关系式，提炼出通项公式的概念，对于第1、3、5个数列，学生能感受到项和序号之间是对应的，但说不出具体关系式，体会并不是每一个数列都可以写出通项公式的.）

【课堂片段3】

生2：有，它们是一一对应的关系.

教师：都是一一对应的关系吗？

生众：不是，第6个数列是多对一.

教师：一对一和多对一让你想到了哪个知识点？

生众：函数.

教师：你能得到项和序号之间的具体的关系式吗？

生3：第2个是a_n=-（1/2）ⁿ，第4个是a_n=100-2n，…，哦，不对，应该是a_n=100-2（n-1），第4个是a_n=-1，其他我就不会了.

教师：好的.同学们看这些式子有点像函数里面的——解析式，对了，那么你求解析式的时候仅仅考虑一个式子吗？

生众：哦，还要考虑定义域.分别是…

教师：那么其他的三列数有对应关系吗？感觉有但是说不出来.

生4：（举手）老师，第5个我也能写出来，根据前面几项的规律，an=1+2+3+…+n.（课堂出现的意外惊喜）.

引导学生抽象出数列的通项公式后，教师给出一个练习：请你写出数列：1，-1，1，-1，…的一个通项公式.

学生的表现也非常棒，举出了a_n=（-1）^n-1，a_n=（-1）ⁿ⁺¹，a_n=sin（2n-1）π/2，a_n=cos （n-1）π等这些数列的不同的表示形式，切实体会了结论2：“一个数列的通项公式有时不唯一”.

问题4：第1个和第3个数列中的项与序号的对应关系是函数关系吗？

（设计意图：回顾函数的概念，通过分析数列的定义域、值域、对应关系，将数列纳入函数的范畴，引导学生用函数的眼光来看数列，用函数的表示方法来表示数列，如用列表法或图像法来表示第1个数列；通过直观感知，分析比较，理解数列是特殊的函数——离散型函数，为后续类比函数的研究套路来研究特殊数列和应用数列模型解决问题打下基础.）

课堂上还真有学生提出不同意见：“数列不是函数，因为函数是连续的，数列是不连续的”，最终在师生和生生的交流、辨析和补充中完成对概念的认识和理解.

3如何彰显章引言课的作用章引言一般从学生的生活现实或学生能理解的实例出发，简单地介绍本章节要学习的内容、地位和作用，同时又从数学文化的角度，揭示与本章内容有关的人文背景、数学应用价值以及其中蕴含的数学基本思想方法，所以章引言也是学生学习本章内容的起始课，是本章知识的核心内容和生长点.

数学文化是人类文明的一个重要组成部分，新课标把“数学文化”融入数学课程内容之中.而数列承载着很多文化背景，古代埃及、巴比伦、中国和印度的文献中都有丰富的数列问题，教材在编写本章内容的过程中，特别注意引用或改编数学史中的例子，不仅丰富了本章内容，而且有利于提升学生的人文素养.

笔者思考：① 如何在本节课中体现数学文化的功能，激发学生的数学学习兴趣和热情？② 如何让学生体悟出学习一个新的数学对象的研究方法，体会其普适性、应用性和有效性？

对于第一点，渗透数学文化，除了问题情境中的毕达哥拉斯三角形数，还在本节课后留了一个课外拓展题：“谢尔宾斯基三角形是一种分形，它是由波兰数学家谢尔宾斯基在1915年提出的.取一个实心的三角形，挖掉由每条边中点组成的三角形，进而继续在新生成的三个小三角形中继续挖，如此循环.你能发现图形中蕴含的数列吗？如果有，你还会继续提出哪些需要深入研究的问题？”

（设计意图：在建立了数列的概念之后，引导学生用数学的眼光来发现问题，用数学的思维来提出问题，为用数学的方法解决问题做好铺垫.）

对于第二点，要让学生有自觉的认识，就要让学生深入具体概念和原理的生成情境中，充分体验分析、归纳、概括、数学表达、辨析等过程，在过程中建立对概念和原理的清晰、准确的认识.本节课概念生成的过程，也就是让学生经历“背景分析和共性归纳——下定义——数学表达——概念辨析”的全过程，在课堂小结中让学生梳理了此过程，并类比函数的研究路径，对数列即将要研究的内容和方法进行了展望，并迁移到研究新的数学对象的一般方法.

反思：章引言的另一个比较大的教学功能体现在“帮助學生了解本章学习的内容、地位和作用”，笔者没有深入思考，听了张老师的课，觉得张老师的开篇设计正好弥补了这个缺憾.具体如下：

从人教A版选择性必修第二册的封面“海螺图象”提出问题：对这一事物或现象，你能提出哪些问题？引入主题：数列.

根据以往的经验，如何从整体上认识“数列”这一新内容的学习？引导学生思考可能研究的内容是数列的产生，数列的本质，数列的价值，数列的内容，数列的思想方法和研究路径……

以两个生活实例引入，一棵树每年同一时刻记录的高度，一个学生的六次测验成绩，体会数列来源于现实的生产、生活需要.并让学生自己举出几个类似的按顺序排成一列的数，研究其变化规律.

由于是借班上课，学生的应答不是很顺畅，但如果每个章节起始课都是这样上，长此以往，相信学生的学习能力、归纳迁移能力都会有很大的提高.

聚焦新课标，研读新教材，践行新理念，应落实到平时的每一节课堂，让我们的研究落地生根、开花结果.参考文献：

［1］ 史宁中，王尚志.普通高中数学课程标准（2017年版）解读［M］.北京：高等教育出版社，2018.

［2］ 渠东剑.函数主题下的数列单元教学的思考［J］.中学数学教学参考，2022（19）：1418.

［3］ 孙朝仁.“章引言”数学教学的哲学思考［J］.上海教育科研，2015（9）：7375.

［4］ 章建跃.高中数学教材落实核心素养的几点思考［J］.课程·教材·教学，2016，36（7）：4449.

［5］ 彭上观.高中数学新课标实验教材使用情况的调查分析［J］.数学教育学报，2005（4）：4547.

［6］ 郭玉峰，赵坤.数学核心素养在高中教材习题中的表现研究：以“函数”为例［J］.教育科学研究，2019（3）：6874.