入口温度对倾斜圆管内超临界CO2 的流动传热影响研究*

董文志 韦 武 周亭羽 巴 金

（贵州大学机械工程学院 贵阳 550000）

1 引言

近年来，超临界流体，特别是水和二氧化碳，因其独特的热物理性质，一直被视为核反应堆、制冷系统、汽车空调和热泵循环中的最佳传热介质［1］。超临界二氧化碳（supercritical carbon dioxide，S-CO2）是一种不可燃、无毒的流体，具有高热效率，且其超临界状态较其他工质更易实现，因此被广泛应用于新一代布雷顿循环电厂［2］。

由于在超临界压力下流体的热物性会发生巨大变化，因此超临界流体的传热与理想流体相比有很大的不同。早在20 世纪50 年代，CO2就被选做冷却剂用于气冷堆动力装置，此后有关S-CO2在竖直圆管内的流动传热规律的研究受到大量学者的重视［3～5］。然而，S-CO2在倾斜圆管内的流动换热特性因受到浮升力和重力影响变得极其复杂。因此，针对不同入口温度条件下S-CO2在倾斜圆管内流动传热的研究对新型换热装置的设计和安全运行及其重要。

截至目前，国内外许多学者主要针对倾斜圆管内超临界压力水的流动传热规律进行了大量实验和数值模拟研究［6～8］，此外，少部分学者也对S-CO2在倾斜圆管内的流动传热进行了数值研究，闫晨帅等［9～10］对S-CO2在倾斜圆管内向上和向下的流动传热行为进行了数值计算，通过获取圆管横截面内速度分布、物性分布和湍流分布等参数分析了S-CO2在倾斜圆管内不同方向流动时顶母线和底母线壁温分布产生差异的原因，确定了类气膜厚度、湍动能和轴向速度等是影响S-CO2传热过程中壁温分布的主要因素。杨传勇等［11～12］通过数值模拟研究了恒定热流密度条件下S-CO2在不同倾斜角度的微细圆管内流动换热特性，并分析了不同的热流密度和质量流速对流动换热规律的影响，通过水平圆管中浮升力判据，等到了浮升力对对流换热的影响规律。Forooghi 和Hooman［13］采用数值模拟方法研究了浮升力对S-CO2在倾斜管内对流换热的影响，结果表明，在垂直管道中，湍流扰动和传热受损的机理与倾斜管道相同，但当倾斜角度小于60°时，湍流扰动和传热受损影响较小。Yang 等［14］对S-CO2在冷却条件下不同倾斜角度微细圆管内的流动传热进行了数值模拟，研究表明，在地球的重力环境下S-CO2的传热性能最佳，随着重力加速度的减小倾斜角度对传热的影响减小。

上述文献综述表明，现有研究大多是针对S-CO2在管径小于10 mm的微细倾斜圆管内的流动传热，关于流动工况对S-CO2在大直径(≥10 mm)倾斜圆管内流动传热的影响缺乏系统研究，本文运用计算流体力学（Computational Fluid Dynamics，CFD）对流体域内部参数进行研究，重点不同入口温度对S-CO2在大直径倾斜圆管内流动传热的影响。研究结果不仅可以为新型换热装置的设计和安全运行提供理论参考，还为超临界流体流动传热提供理论基础。

2 数值方法与模型验证

2.1 控制方程与计算方法

本文数值计算模型可由连续性方程、动量守恒方程和能量守恒方程进行描述，稳态状态下的张量形式具体如下：

连续性方程：

动量守恒方程：

能量守恒方程：

上式中u，ρ，ℎ，μ，λ，cp，f和ST分别代表流体的速度、密度、比焓、动力粘度、导热系数、比热、单位质量力和粘性耗散项。

湍流模型的选择湍流模型的选择会直接影响S-CO2流动传热的数值模拟结果，Wang等［15］对不同湍流模型进行了计算，结果表明采用SST k-ω低雷诺数湍流模型可以得到比其他湍流模型更精确的计算结果。因此，本文选择SST k-ω低雷诺数湍流模型进行数值模拟。为了保证数值计算结果的准确性，本文的流体热物性参数来源于美国国家标准与技术研究NIST REFPROP 数据库，采用分段线性插值（piecewise-linear）方法自定义流体的热物性。在超临界压力下模拟CO2的对流传热问题较难收敛，为了保证数值计算能完整收敛，本文采用基于压力-速度耦合的SIMPLEC 算法，压力项离散格式采用Body Force Weighted，密度项离散格式采用Second Order Upwind，动量方程和能量方程的离散格式采用QUICK，其余的算法保持默认。收敛标准为连续性方程、动量方程、能量方程以及湍流参数方程残差低于10-6。

圆管局部换热系数ℎ 定义为

主流温度Tb定义为

式中，Tw为壁面温度，K；Tb为主流温度，K；A，为圆管横截面面积，m2。

2.2 计算模型与验证

倾斜圆管的物理模型如图1 所示，由入口绝热段和加热段两部分组成，其中入口绝热段是为了保证加热段入口流体处于充分发展状态。圆管直径d=22.14 mm，入口绝热段长度Lad=1220 mm，加热段长度Lℎ=2440 mm，并以圆管轴向倾斜角α=30°为例进行仿真计算。圆周角标记为θ，θ=90°和θ=-90°分别代表圆管顶母线和底母线。其中边界条件设置如下，入口为质量流量入口，出口为压力出口，绝热段与加热段管壁分别设置为绝热边界与恒定热流密度，运行压力视为定压。

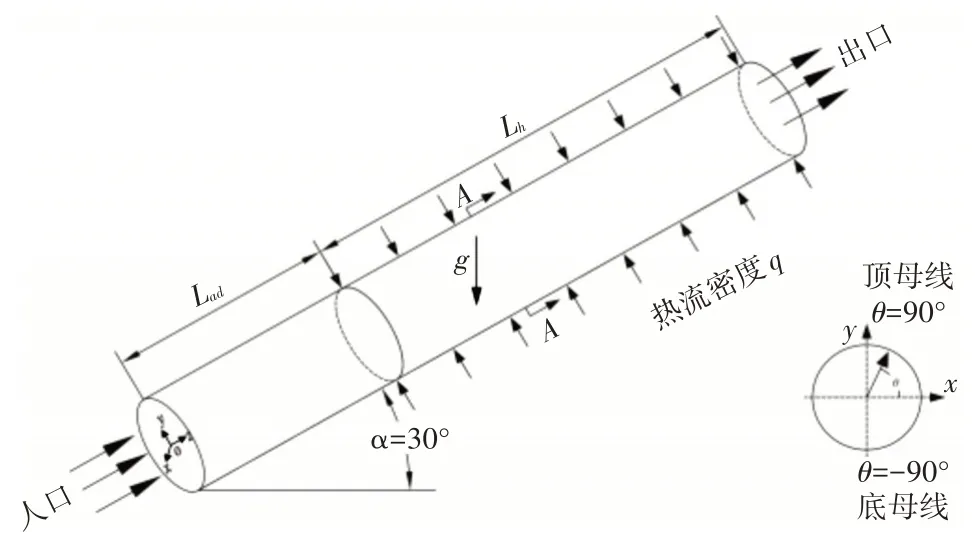
图1 物理模型

为了保证计算结果不受网格数量的影响，需要对网格进行敏感性验证。近壁面处温度梯度较大，加之其流动接近层流，粘性起主导地位，必须确保壁面首层网格的y+≈1。本文利用ANSYS ICEM对网格进行划分，轴向及径向网格示意图如图2 所示。其中圆管截面采用O-Grid 方法划分，能够完美解决圆柱中心网格扭曲率太大的问题，轴向采用均匀划分，径向采用非均匀网格且越靠近壁面网格尺寸越小。通过改变径向、周向、轴向网格数量，创建了三套疏密程度不同的网格，具体参数设置如表1所示。

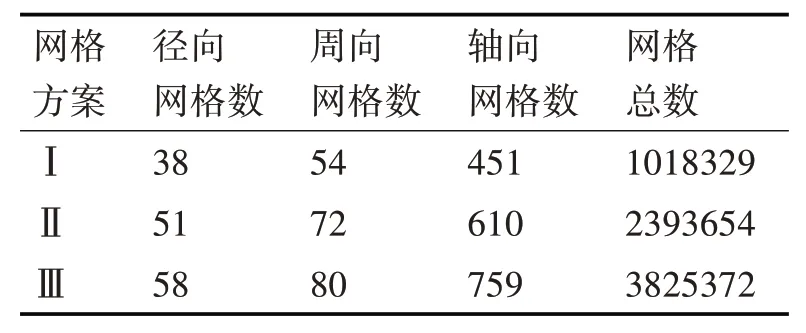
表1 网格划分参数

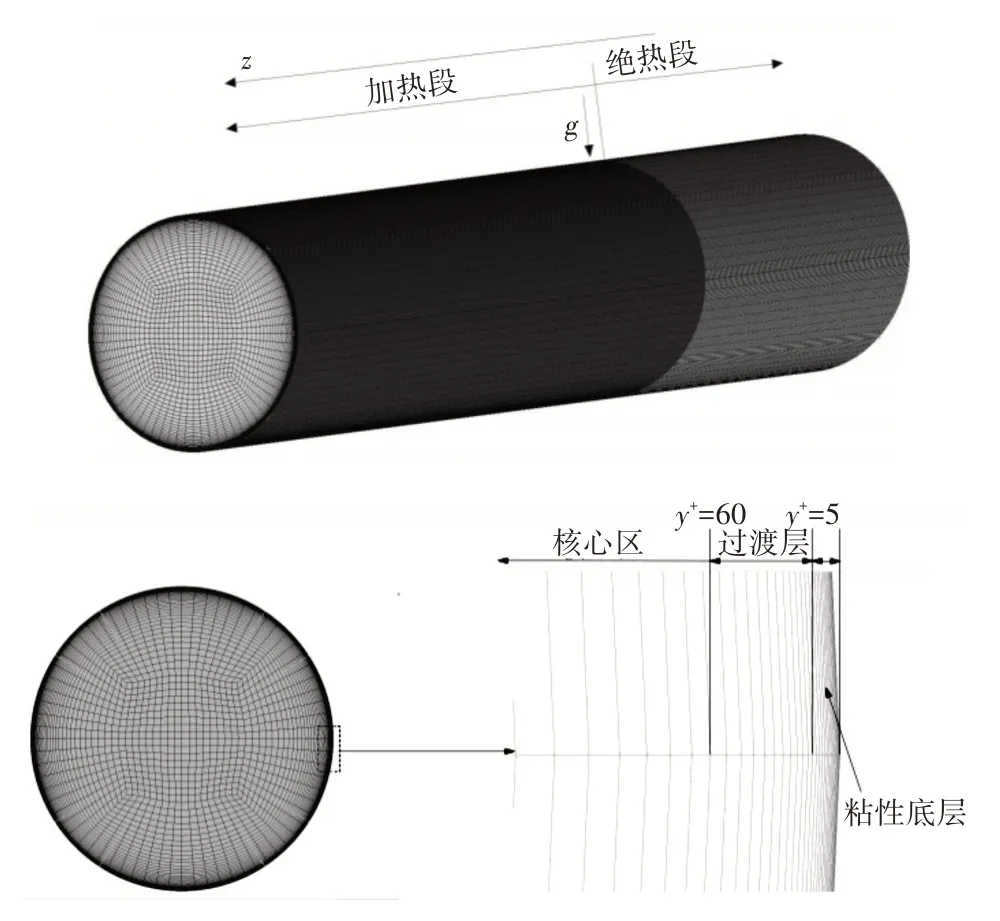
图2 网格局部视图

为了验证模型的正确性，首先对S-CO2在α=0° 的水平圆管内的流动传热进行模拟，并与Adebiyi［16］的实验结果进行对比，其中验证计算的工况为热流密度qw=15kW/m2，压力P=7.59MPa，质量流率G=0.148kg/s，入口温度Tin=288.55K 。图3 为不同网格类型时，水平圆管顶母线与底母线内壁温度沿加热段轴向分布情况，其中横坐标中zℎ代表加热段起始点至出口处的轴向距离，从图中可以看出，三种不同类型网格的数值仿真结果与实验数据吻合较好，验证了计算模型的正确性。为了减少计算成本且保证计算精度，本文选用网格方案Ⅱ进一步深入研究。

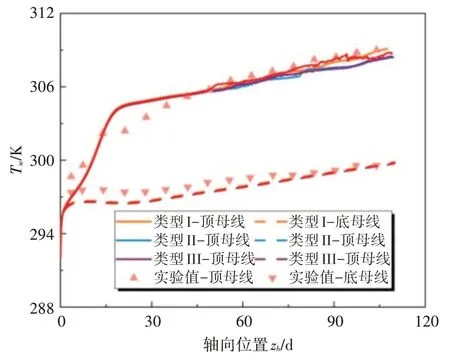
图3 网格敏感性分析

3 计算结果及分析

3.1 S-CO2热物性

当压力高于临界压力时，随着温度的升高，CO2将从液态持续转变到超临界状态。临界点附近微小的温度改变都会导致流体热物性的急剧变化，其传热特性也因此不同于定物性流体。图4 给出了CO2在P=7.59MPa 下的热物性参数随温度的变化关系。从图中可以看出，定压比热随温度的变化异常剧烈，当压力接近流体的临界压力时，定压比热值达到最大值，该点温度定义为类临界温度Tpc，此时，流体吸收的热量主要是用于流体的膨胀体的膨胀，而非提高自身的温度，因此密度、导热系数和粘度系数在临界温度附近剧烈变化。伪临界区域的密度变化可导致流体热膨胀和加速浮升力的作用，从而对流体的流动和湍流特征产生重要影响。

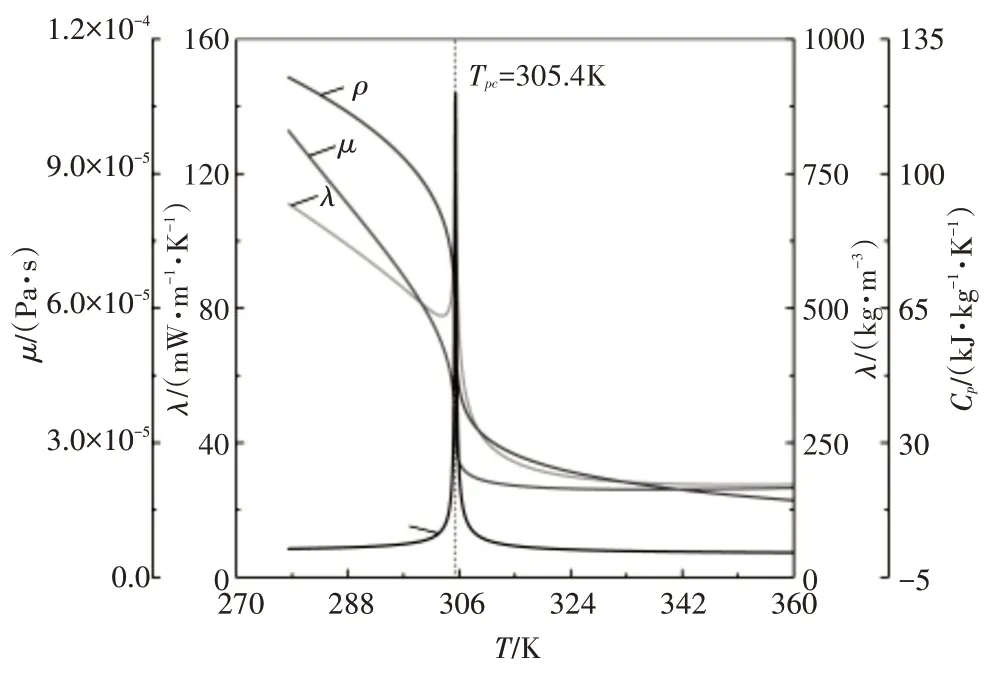
图4 CO2在P=7.59MPa 下的热物性曲线

3.2 S-CO2在倾斜管内的传热特性

倾斜圆管内S-CO2对流传热表现出了不同的传热特性，本节以S-CO2在恒定热流密度加热条件下，倾斜角α=30° ，P=7.59MPa ，G=0.3kg/s ，qw=30kW/m2，Tin=289.15K 作为基准工况，以获得倾斜管内S-CO2的温度场和流场进而分析其传热特性。图5为S-CO2在倾斜管内顶母线与底母线的温度与换热系数沿轴向加热段分布规律，从图中可以明显看出，温度分布沿加热段轴向方向成非对称分布，加热段入口区域顶母线壁面温度快速上升，到达加热段中段时壁面温度逐渐平稳上升，而底母线壁面温度持续平缓上升。随着管壁持续在恒定热流密度加热条件下，顶母线壁面温度大于底母线，且壁面温差波动越靠近出口区域越小。另外，顶母线与底母线换热系数与壁面温度分布呈相反的变化趋势。

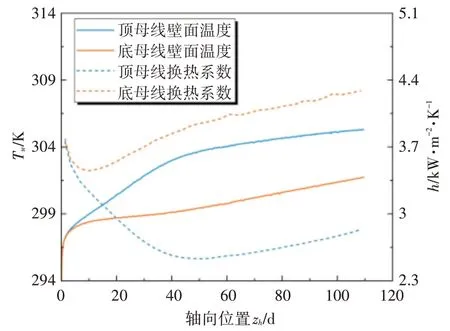
图5 顶母线与底母线壁面温度与换热系数轴向分布曲线

图6 为倾斜圆管在局部加热段区域内zℎ=10d、zℎ=45d和zℎ=80d速度矢量分布及速度云图，从图6 中可以看出，倾斜圆管内部流体速度呈现出顶部小底部大以及轴向速度越靠近加热段出口区域速度越大的特点；从速度矢量分布可以明显看出，横截面两侧出现二次环流现象，造成流场分布不均的主要原因是，近壁面区域附近的S-CO2率先被加热升温，流体密度随之下降；中心区域流体升温较慢，密度较大，与近壁面区域的流体形成密度差，此时受到圆管倾斜与浮升力的双重影响，造成圆管底部高温、低密度且传热能力差的流体沿管壁两侧向圆管顶部流动，圆管中心区域大密度流体向底部流动，故横截面内出现二次环流现象。因此，浮升力和二次环流是顶母线壁面温度高于底母线的主要原因。

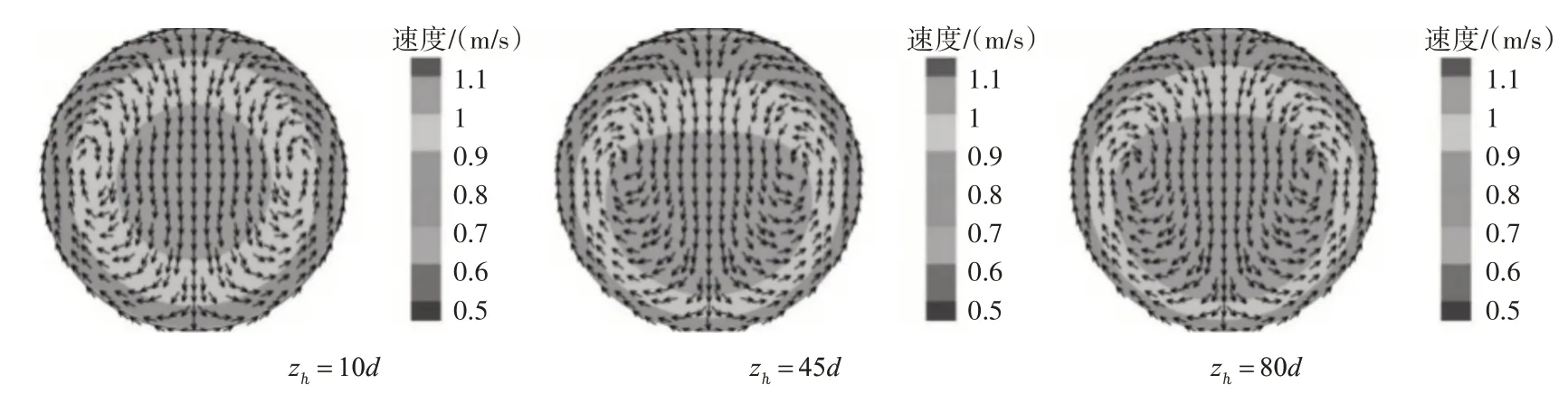
图6 局部加热段矢量速度及速度分布

3.3 入口温度对传热性能的影响

在保持其他工况不变条件下，分别设置了Tin=289.15K ，Tin=294.15K ，Tin=299.15K 研究不同入口温度对倾斜圆管内S-CO2流动传热的影响。图8 为不同入口温度下底母线与顶母线的温度和换热系数沿轴线方向分布情况，由图7 可以看出，随着入口温度的增加，顶母线于底母线壁面温度和换热系数整体水平不断提高。同时，顶母线壁面温度急剧上升区域与换热系数最小值逐渐向加热段入口区域前移。本文采集了加热段中下游部分的壁面温度和换热系数数据，如表2 所示。分析结果表明随着入口温度升高，上下两侧温差不断减小，换热系数也不断提高，主要原因是入口温度升高，倾斜管内中心区域流体温度与近壁面区域流体温度差缩小，进而由密度差引起的浮升力减弱，导致了顶母线与底母线壁面温差减小，传热恶化现象得到有效控制，因此入口温度对倾斜管内S-CO2的传热性能影响的极其重要。

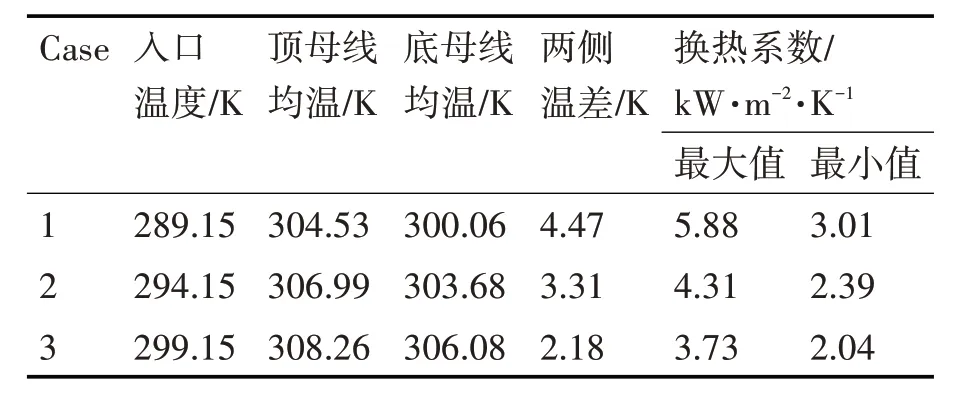
表2 不同入口温度结果分析

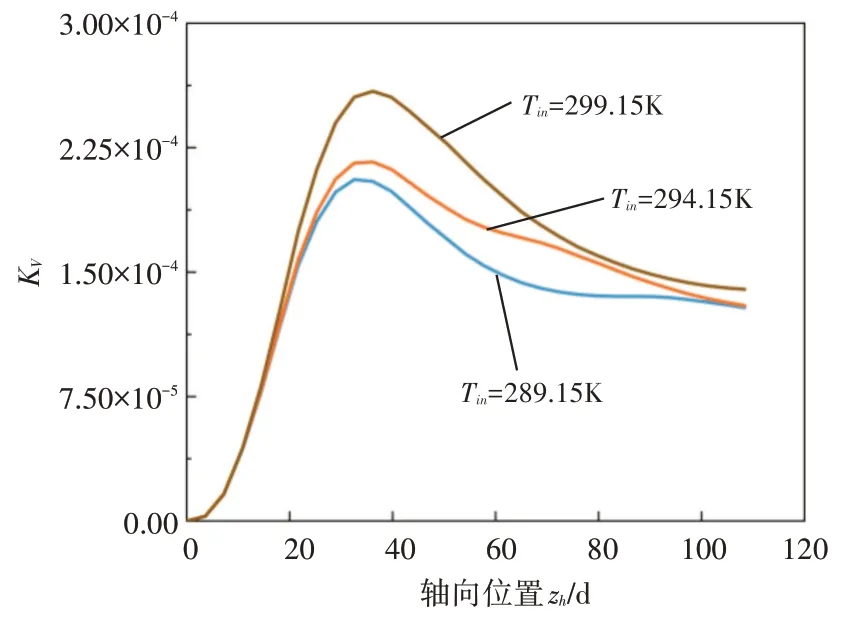
图8 不同进口温度下相对二次流动轴向分布曲线

根据3.2 节中的计算结果可知，倾斜圆管内二次流现象显著，为了定量的说明倾斜圆管横截面内二次流对流动传热的影响，本文引入相对二次流动能参数Kv来表示二次流的大小［17］，Kv定义为

式中，u、v和w分别表示倾斜圆管内横截面沿x、y和z方向的速度分量。

图8 展示了不同入口温度条件下相对二次流动能参数Kv沿加热段轴向位置的分布曲线，从图中可以明显看出，不同入口温度条件下相对二次流动能的变化趋势相同，首先在加热段入口区域快速上升达到最大值，然后沿着轴向方向逐渐减小且呈现出较小幅度的变化。此外，入口温度越高，Kv总体水平越高，该现象表明入口温度升高会导致横截面内更多的密度低且传热性能差的流体沿着管壁两侧流向顶母线区域，从而导致了顶母线壁面温度在加热段入口区域温度快速上升，加热段中部及出口区域则平稳上升。

4 结语

为研究不同入口温度对倾斜管内S-CO2对流传热的影响，本文通过壁面温度、换热系数、湍动能、轴向速度及相对二次流动能等流动传热参数分析了倾斜管内S-CO2在不同入口温度条件下的流动传热特性。随着入口温度升高，倾斜管内中心区域流体温度与近壁面区域流体温度差缩小，进而由密度差引起的浮升力减弱，导致了顶母线与底母线壁面温差减小，传热恶化现象得到有效控制。

为研究入口温度对流动传热恶化现象，本文研究了入口温度对相对二次流动能的影响。研究发现，由于入口温度升高，造成了相对二次流动能总体水平提高，从而导致了横截面内更多的密度低且传热性能差的流体沿着管壁两侧流向顶母线区域，增加了底母线附近传热效果，因此入口温度起到强化传热，降低传热恶化现象的发生。