无线通信中基于卷积神经网络的负载均衡系统*

朱明浩 李 君 李正权 仲 星 张茜茜 沈国丽

（1.南京信息工程大学电子与信息工程学院 南京 210044）

（2.无锡学院电子信息工程学院 无锡 214105）

（3.江南大学轻工过程先进控制教育部重点实验室 无锡 214122）

（4.北京邮电大学网络与交换技术国家重点实验室 北京 100876）

1 引言

随着互联网技术的发展和进步，越来越多的数据请求和用户数量给无线通信系统带来了许多挑战［1］。为应对这些挑战，在多小区多用户系统中，如何进行合理的资源管理是近年来值得深入研究的方向。

目前的资源管理方式围绕用户关联［2～9］、功率控制［10～14］等展开。由于基站与用户的关联状态是二进制变量，导致求解的用户关联问题是非凸的，于是通过优化问题的关联状态从二进制变量松弛成离散值可以将原非凸问题转化为凸优化问题求解［3～5］。为实现效用函数的最大化在蜂窝网络中对优化问题开发了集中式用户关联策略［4］。结合匹配理论，提出了一种基于图论的用户关联优化方案［5］。此外，还提出了一种理论平均比例公平效用来解决用户关联问题［6］。但上述内容并没有考虑到基站之间的负载均衡问题，随着今后用户数量的不断增加，基站之间的负载不均衡而导致基站过载或空载的问题将愈发突出［10～13］。于是在匹配理论的基础上，文献［7］提出了一种基于匈牙利算法的用户关联方法，以实现宏基站与微基站的负载均衡，通过为优化问题设计权重系数，来实现宏基站和微基站之间负载均衡和信号干扰噪声比（SINR）的动态调整。在最近的研究中，对偶分解方法被广泛用于用户关联策略中。为了实现基站间的负载均衡，通过约束基站关联的用户数的上限，再松弛约束条件将原问题转化为凸优化问题结合用拉格朗日对偶分解和舍入方法得到用户关联策略的可行解［8～9］。然而，由于当前算法通常在求解过程中需要多次迭代才能实现收敛，这导致实际应用时计算复杂度高，无法适用于目前低延迟的通信网络环境［14～18］。

本文在提出优化问题时考虑了基站的负载情况，并利用基于二部图论的KM 算法求解。为了适用于低延迟环境，设计和部署了一种卷积神经网络（CNN）的用户关联算法来降低计算复杂度。最后在实验仿真并将所提方案与传统最大SINR、凸优化取整方案进行比较。仿真结果表明，所提CNN关联方案在负载均衡程度方面更接近基于KM 算法，并优于最大SINR方案、凸优化取整方案的负载情况，同时，具有更低的计算复杂度，适合在低延迟环境中应用。

2 系统模型

2.1 超密集无线网络系统

用如图1 所示，超密集无线网络下行信道系统环境模型。系统模型包括多个基站和多个单天线用户。假设网络中包含B个基站以及U个用户，它们的集合分别为J={1，2…，B} 和I={1，2…，U}。

图1 超密集无线网络系统图

如果用户i与基站j关联，则基站j与用户i之间下行链路的SINR为

其中ℎji是指基站j与用户i之间的信道状态信息，信道状态信息主要包括了基站与用户之间的瑞丽衰落和路径损耗。pc表示基站到用户之间的下行传输功率。表示用户i接收到来自其他基站的干扰信号，j，k∈J，i，l∈I，σ是环境噪声。

我们引入一个维度是i×j的用户关联矩阵x，其中的二进制元素xji表示用户i与基站j是否关联，如果xji=1，则表示用户i与基站j关联，否则为0。在用户i与基站j的信道中，传输信号时实现的速率可表示为

因此，系统的和速率R可表示为

其中我们定义每个基站关联的用户子集，这个子集的集合表示为M={M1，M2···Mj} ，其中Mj代表其基站j所关联的用户子集。

2.2 优化模型

由于关联用户共享基站j的资源，因此基站j到关联用户i的下行速率为

其中，约束项C1 表示xji的值是一个二进制变量。C2表示一个用户最多只能关联一个基站。C3表示各基站关联的用户的累积总和等于环境中的所有用户。

3 算法理论实现

由于第2 节建立的优化问题是一个非凸优化问题，无法直接求解，因此我们提出基于匹配理论的一对一匹配方案，并结合库恩-马克（Kuhn-Munkres，KM）算法进行求解，之后通过收集相应的信道状态信息和关联解，设计训练CNN网络模型并验证其学习能力。

3.1 基于KM算法的用户关联方案

首先用无向图来描述基站与用户的匹配关系。无向图中顶点集合VB和VU分别由基站和用户的集合J和I组成，VB和VU不相交。则基站与用户的关联用无向图表示为G=(VB，VU，E)，匹配边E的两个端点分别连接两个的顶点集合。则原问题（5）的求解转化为求匹配边的权值之和的最大值，每条边的权值为wji=log(log2(1+SINRji))-log(mj)。

由于KM 算法是解决一对一最优匹配问题的有效算法，但无法解决问题（5）的多对一问题［5，19］，因此，考虑将多对一问题转化为一对一问题再结合KM算法求解。我们根据其负载上限扩展基站的顶点集。假设负载上限等于用户总数，则拓展后的基站顶点集为。为了构造加权二部图，使得拓展后的基站和用户的顶点集的点个数保持一致，通过添加虚拟用户，将用户的顶点集扩展为，由于虚拟用户只是配合KM 算法的计算形式，其具体值无意义，所以将拓展出的虚拟用户在权重矩阵w中的位置的值置零。

Prasad N等提出一种转换权重之和的方法［7，15，20］，假设编号从1 到q的q个用户与基站j关联。基站j的虚拟顶点集为Bj，它包含U个虚拟基站点，则任何用户i与虚拟基站m∈关联的权重可以表示为

当q个用户与基站j相关联时，它们的权重之和等价于在中q个用户与Bj的前q个虚拟基站的权重之和，则用户关联问题转化为虚拟基站与虚拟用户的最优匹配问题（7）。

约束项C1 表示用户i只能与一个虚拟基站关联。约束C2确保虚拟基站m最多只与一个用户相关联，C3 表示关联变量是一个二进制变量。求解原始关联问题等价于对最大匹配问题（7）求解。

对于式（7）的最优匹配问题，考虑使用KM 算法［13］求解，其复杂度远小于穷举法。得到式（7）的解后，将矩阵按列平均分成B部分，每部分为U行，然后观察矩阵的值，如果最优解中第a行的b部分的值为1，a∈(1，U)，b∈(1，B)，则设xba=1，遍历每行后，得到基站与用户的关联策略xji。通常KM 算法求解匹配问题的时间复杂度为O((max(U，B))3)，由于基站和用户的顶点集都扩展为U×B，所以所提方案的时间复杂度为O((UB)3)。

3.2 基于CNN关联方案的设计训练

在上一小节KM 用户关联策略的基础上，本文提出基于CNN 的关联算法来减少关联算法的计算复杂度，通过设计基于CNN 的用户关联策略，学习基站与用户信道状态信息到关联策略之间的非线性映射关系。

所提CNN网络模型结构如图2所示，CNN的结构主要分为输入部分、卷积全连接部分和输出三部分。输入层负责接收基站与用户之间的信道状态信息，隐藏层包含卷积层和全连接层，卷积层负责提取输入信号的有用特征，每一层由多个卷积核组成，全连接层负责对卷积层的输出数据进行泛化拟合，各层输出前通过附加的激活函数ReLU 来提高神经网络的非线性能力。为了实现输出层的功率预测值在［0，1］之间，末端的输出层附加sigmoid 激活函数再取整。

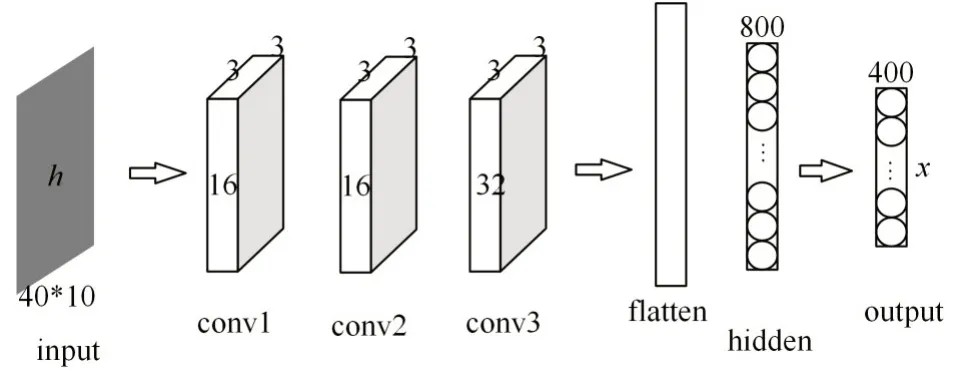
图2 所提CNN的网络结构

CNN的训练过程包括数据集的收集、网络训练和测试。确定用户关联策略后，收集基站与其关联的用户之间的信道状态信息ℎ，以及相应的最优关联策略x。收集信道状态信息和相应最优关联结果作为数据集，形成一组训练数据集，重复1 万次生成所需的训练数据，然后将训练数据集送入输入层，通过神经网络的前向传播过程得到输出值，构建输出层的输出值与最优关联的均方误差（MSE）作为损失函数来描述神经网络的训练水平，结合反向传播（BP）算法自动调整神经网络的权重参数，所提出的方案使用Adam方法来寻找最优权重系数。

训练过程如图3 和图4 所示，根据损失值的反馈不断调整神经网络的超参数包括学习率（LR）、批次大小（Bach size），发现当网络模型的学习率为0.0001、批次大小为200时，损失值趋于稳定且最小。

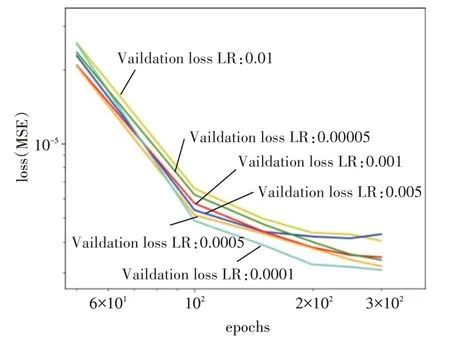
图3 不同学习率下模型误差情况

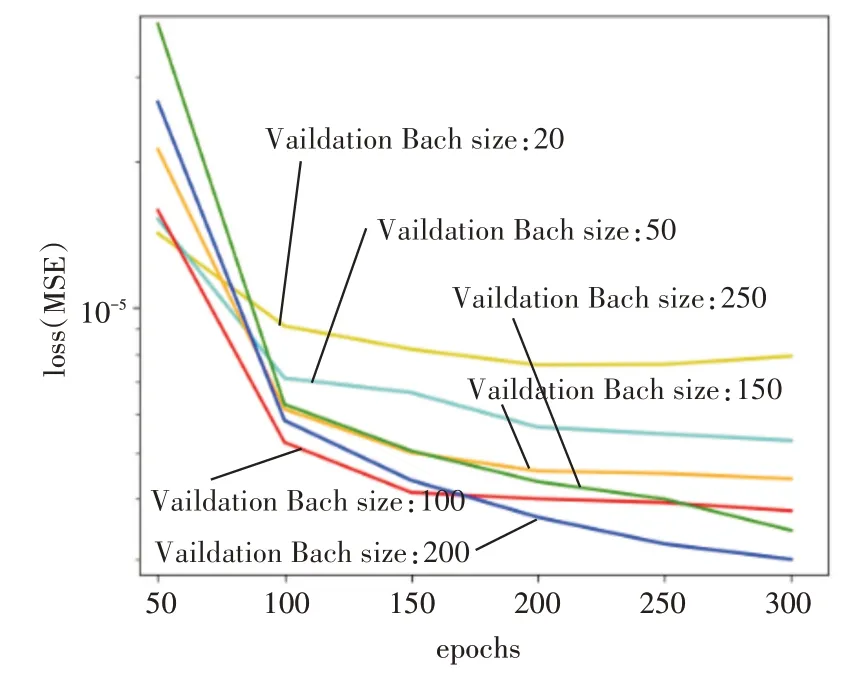
图4 不同批次大小下模型误差情况

为了验证所提CNN 的对局部特征的学习能力，训练了DNN模型作为比较对象，如图5所示，所提CNN 模型在训练、测试数据集上的准确率优于DNN 模型，其中DNN 的准确率稳定在97.5%，而所提CNN稳定收敛在98.6%。

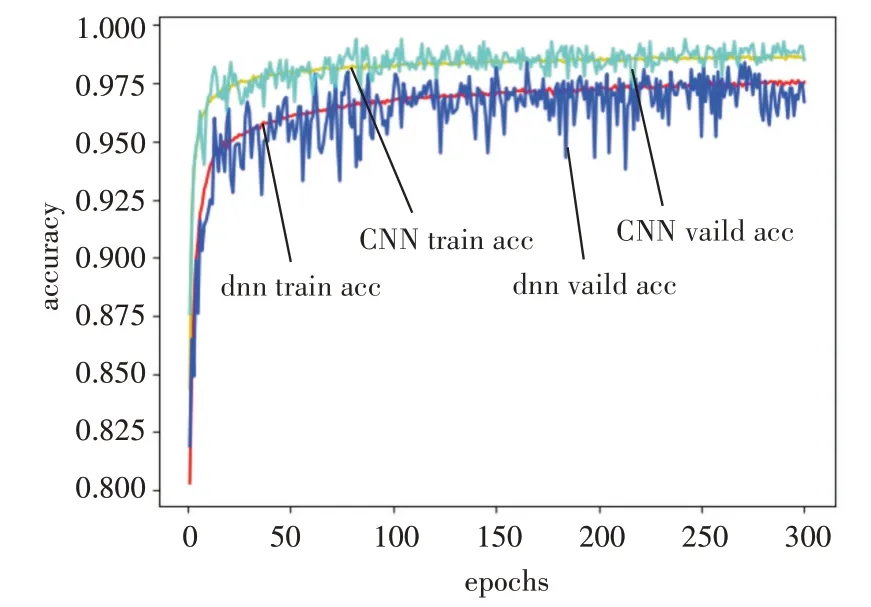
图5 所提CNN与DNN模型的学习准确率

4 仿真测试

本文利用Matlab 和Python 仿真软件建立了一个超密集无线网络系统模型，参数设置如下：所考虑的下行环境包括10 个基站和40 个单天线用户，各基站的总发射功率Pc为20W，噪声功率密度为0.5W［19］，基站和用户的位置随机部署在1000m×1000m 的覆盖范围内［7］。用户与基站之间的路径损耗参考128.1+37.6 log10d［20］，其中d为基站与用户之间的距离。

为了验证所提方案的负载均衡能力，将所提CNN 方案与所提基于KM 算法、最大SINR 关联策略以及凸优化取整方案［8］进行比较分析，下面给出具体的仿真结果，并对结果进行分析。

4.1 用户与基站的关联剖面

图6 展示了未考虑负载均衡的最大SINR 方案剖面图，其中部分基站关联不到用户，处于空载状态，基站间的负载不均衡。因此，我们提出用户关联的负载均衡方案来改善图6 中出现的负载不均问题。

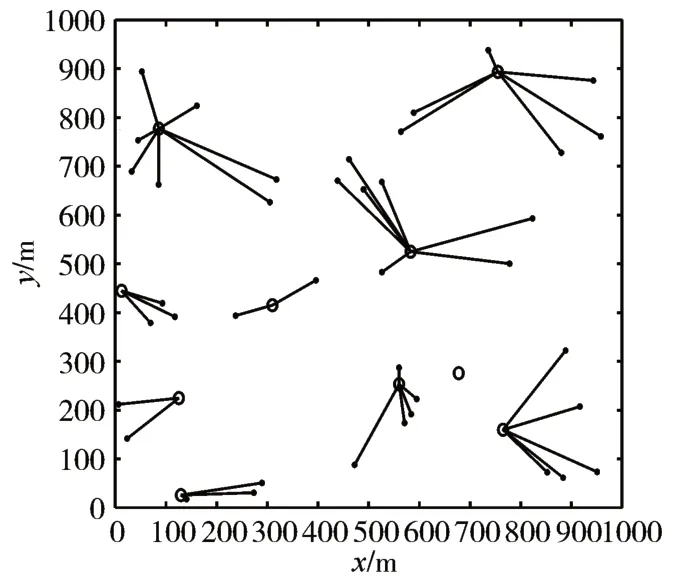
图6 最大SINR方案关联剖面图

图7、8、9 分别展示了凸优化取整［8］、基于KM算法、所提CNN 模型下基站与用户的关联状态。通过比较关联剖面可以发现，图6 中原先关联不到用户的基站在图7、8、9 中有用户关联，基站间关联用户的负载相对更加均衡，减少了图6 中基站的空载现象，提高了基站的利用率。

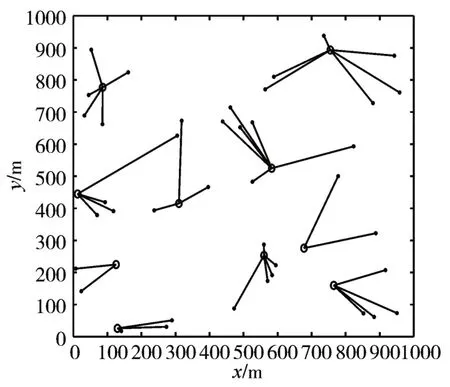
图7 凸优化关联剖面图

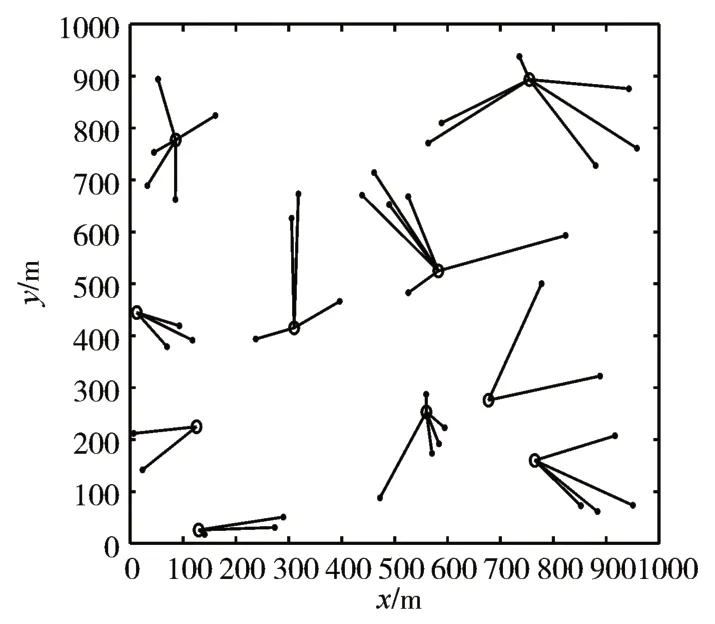
图8 所提基于KM算法剖面图

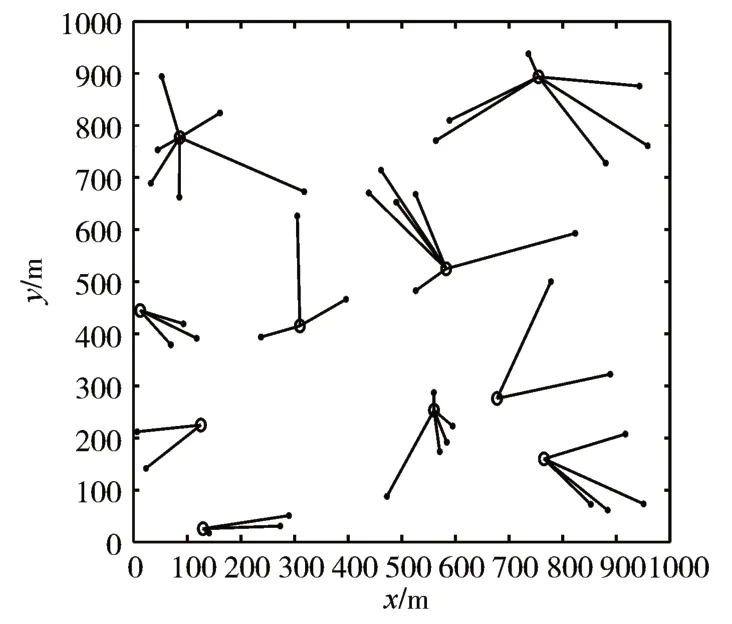
图9 所提基于CNN算法剖面

4.2 测试负载均衡

为验证所提方案在不同环境下负载均衡的能力，分别比较了在四种关联方案下，环境中基站数分为10、20 时，随着用户数的增加各环境内的负载情况，我们以基站关联用户数的方差作为衡量负载均衡程度的指标，分析不同方案在多种环境下的负载情况如图10所示。

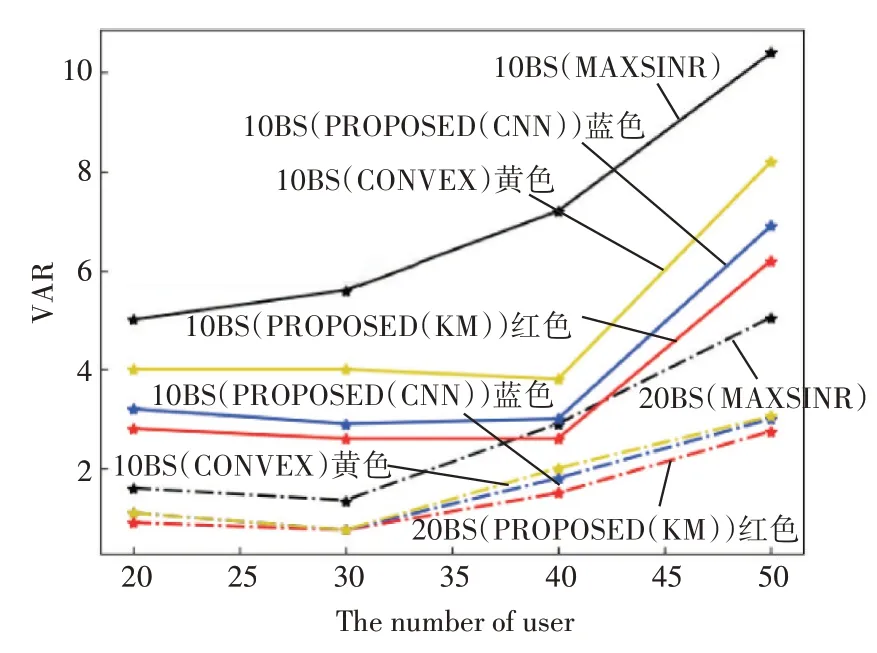
图10 多环境下不同算法的方差

在图10 中，我们用不同的线来区分基站环境，实线代表10基站环境，虚线代表20基站环境，另外用不同颜色来区分不同方案，黑色线代表最大SINR 方案，红色线代表本文所提基于KM 方案，蓝色线代表所提CNN 模型，黄色线代表凸优化取整方案［8］。从整体看，随着环境内用户规模的不断增加，各方案的方差整体趋于上升趋势，这意味着用户数越多基站间的负载情况往往越差。其次虚线的方差往往小于实线，这意味着20 基站环境的负载比10 基站的更均衡，验证了基站密集化可以有效缓解负载不均问题。最后，我们分析不同方案间的负载均衡能力，当基站数量等于10（实线）时，红线代表的所提KM方案的方差值与黑线（最大SINR方案）和黄线（凸优化取整方案）相比最小，而所提CNN模型的方差也小于上述两种方案。同样，在基站数量为20（虚线）时，所提方案也有同样的表现，这意味着所提CNN 网络模型，相比其他方案，基站之间的负载更加均衡。总之，所提CNN 网络模型在不同环境下相比其他用户关联方案实现了相对更均衡的负载。

表1 各方案计算复杂度比较

4.3 计算复杂度分析

最后，以CPU的运行时间作为衡量指标比较了所提CNN 网络模型与基于KM 算法方案的计算复杂度。

如表1 所示，随着环境内基站、用户规模的增加，基于KM 算法的关联方案的计算复杂度越来越高，运行时间也越来越长，这是由于KM 算法需多次迭代才能实现收敛，用户数越多，迭代次数也更多，所以运行时间就越长，而所提CNN 模型的训练阶段是离线进行的，只有训练好的网络才会在实际场景中应用，所以训练时间不需要考虑在计算时间中，另外如表1 中所示，训练好的神经网络不会因为用户数的增加而影响其计算复杂度，适合在实时场景中应用，并且用户数越大，这种优势越明显。

5 结语

针对无线通信负载不均衡提出了一种实现负载均衡的用户关联算法，本文将基站的负载纳入到优化问题中考虑，并将其转化为基于KM 算法的最优匹配问题，由KM 算法求解，为了满足低复杂度、低延迟环境需求，设计训练了CNN 模型。仿真结果表明，所提方案降低了基站间关联用户数的方差，实现了基站间相对更均衡的负载情况，相比基于KM 算法，所提CNN 模型对其学习程度达到98.6%，同时计算复杂度更低，既实现了快速可靠的用户关联，又实现了负载均衡。