改进二进制粒子群算法在配电网重构中的应用

束成文，朱金荣

（南京工程学院电力工程学院，江苏南京 211167）

配电网是电力系统的重要组成部分，它连接着配电变电站与用户端，为各类用户提供电能，其安全可靠运行是十分重要的。配电网的重构研究是实现配电网可靠高效经济运行的重要措施之一[1-3]。近年来，随着分布式电源(Distributed Generation，DG)的快速发展，为了提高配电网的安全性与电能质量，大量DG 被接入到配电网中，这使得传统数学算法在复杂的配电网中不再适用，国内外学者常采用人工智能算法来进行配电网优化。文献[4]采用算数交差算子改进遗传算法，并运用于配电网重构中；文献[5]在IEEE33 节点配电系统中引入改进灰狼算法，降低了系统网损；文献[6]在配电网重构中采用了人工鱼群算法，有效地降低了经济成本。

综合考虑已有研究，以有功网损和节点电压偏移作为目标函数，建立配电网重构模型，并对传统二进制粒子群算法(Binary Particle Swarm Optimization，BPSO)进行改进，在IEEE33 节点配电系统上进行分析，可以有效增强算法性能，提升网络重构效率。

1 配电网重构模型

通过改变配电网中开关分合状态，达到有功网损与节点电压偏移最小的目标。配电网重构模型需要考虑优化目标与约束条件，具体如下：

1）有功网损最小目标：

式中，M为支路总数；Kl为支路l的状态。

2）节点电压偏移最小目标：

式中，M为节点数；Vi、ViN分别为节点i的实际电压与额定电压。

3）综合目标函数，为解决量纲问题，对f1、f2进行归一化，采用加权法将其转化为单目标[7]，可表示为：

式中，f01、f02分别为有功网损和电压偏移的初值；ω1、ω2为各项权重系数。

4）约束条件如下：

式中，gk为重构后的网络拓扑结构，G为网络正常运行条件集合；f(PQV)为潮流约束方程。

2 基于改进算法的配电网重构

2.1 网络编码方式

传统研究中常采用二进制编码策略[8]，但会得到许多不可行解，计算效率低，为了提高算法性能，采用环路编码方式。图1 所示以IEEE33 节点配电系统为例[9-10]，在编码时，每个粒子的维数与开关数相等，用0 和1 表示开关的分合。步骤如下：

1）使配电系统处于正常运行状态；

2）依次闭合第1-5 个联络开关，形成Loop1……Loop5；

3）用变量x表示Loop 中的开关编号。例如集合x1包含了支路2、3、4、5、6、7、18、19、20、33 上的开关。

此外，基于拓扑结构与安全性考虑，进一步化简，则L1对应的简化粒子编码组合为[1111111110]，约束后的可行解空间为15360，不可行解减少，算法搜索效率提高。

2.2 对于不可行解的剔除

接入大量DG 时，会使配电系统变得更加复杂，但配电网辐射状运行的结构不变。基于图论和树状结构的理论分析得出正常运行判据，即闭合支路数=有效节点数-1。通过剔除不可行解提高计算效率。

2.3 潮流计算方法

由于配电网呈辐射状运行[11]，故采用前推回代算法[12]进行潮流计算。

2.4 二进制粒子群算法

1995 年，Kennedy 等人受到鸟类的迁徙和群集行为启发，提出粒子群算法(PSO)解决连续空间域的优化问题。后来为了解决离散空间域的优化问题，又提出了二进制粒子群算法(BPSO)，公式如下：

粒子的位置取0 或1，更新公式为：

式中，Sigmoid(·)为激活函数，其计算方式为：Sigmoid(x)=1/(1+e-x)。

2.5 改进的二进制粒子群算法

传统BPSO 步骤较为简单，易于实现，但是存在早熟、计算能力低等问题，由此做了以下两点改进。

2.5.1 引入自适应比例选择策略

由式（5）可以看出，粒子的位置与速度相关，且只能取0 或1，速度越大则位置为1 的概率越大[13]，而速度又与权重系数ω相关。在基于自适应比例选择法的BPSO 中，引入概率选择因子P来改进ω，使其随着粒子的适应度产生动态变化，以此避免算法早熟，公式如下：

式中，fi表示粒子i适应度值；k为任意正整数。k越小，选择的压力越小，适应度不好的粒子具有生存机会，搜索范围增大；相反k越大，选择的压力越大，适应度不好的粒子将被淘汰，搜索范围减小。

在算法的不同阶段，种群会动态变化，需要引入自适应比例选择策略来计算不同阶段个体被选择的概率。在该策略中，对指数k进行一定的调整，公式如下：

式中，fmax表示最优个体的适应度；表示种群的平均适应度。

采用自适应的比例选择策略，在进化的不同阶段，动态调节k。在第一阶段，由于种群的随机性，fmax与fˉ差距较大，适当减小k，扩大搜索范围，避免早熟；第二阶段，k将自适应地调整，加快种群达到全局最优的速度；第三阶段，fˉ接近全局最优解，k接近于无穷，粒子选择的压力变得无穷大，从而促进算法收敛于全局最优解。

改进后BPSO 的速度更新公式为：

2.5.2 引入混沌搜索

传统BPSO 后期容易早熟[14]，根据混沌变量的初值敏感性和遍历性，可对BPSO 中适应度较差的粒子进行混沌搜索，故将混沌优化中的Logistics 映射公式与BPSO 结合，以扩大粒子的搜索精度，加快收敛速度。Logistics 公式如下：

式中，xk+1、xk分别为第k+1 次、k次迭代的混沌变量；μ为常数4。

优化适应度较差粒子的步骤为：

1）选取上述自适应比例选择策略中适应度较差的粒子；

2）计算粒子i的当前位置ki与适应度最优粒子kr之间的距离：

3）当di小于给定值时（文中取10-3），对适应度较差的粒子执行混沌搜索，用搜索得到的新粒子替换粒子i；否则粒子位置不变。

改进算法流程图如图2 所示。

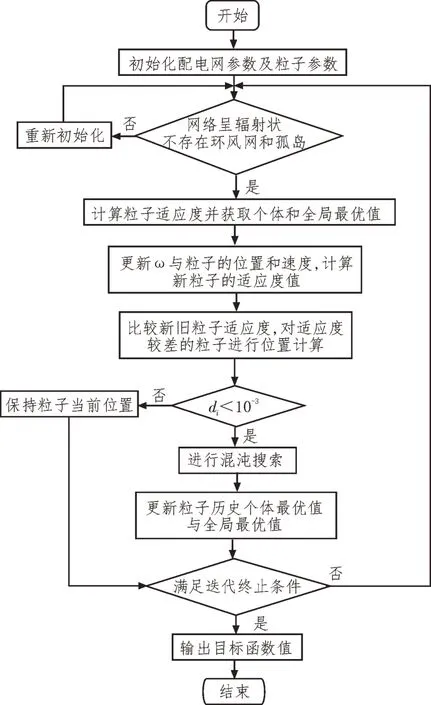
图2 改进算法流程图

3 算例分析

该文以IEEE33 节点配电系统为例进行仿真[15]。算法设置种群规模M=50，最大迭代次数maxiters=100，Vmax=4，学习因子c1=c2=2，权重系数ω根据优化目标的优先级来确定，并始终保持ω1+ω2=1。

3.1 不含DG的重构

在不含DG 的配电系统中，仅以有功网损最小作为目标函数（式（3）中ω1=1、ω2=0），以此来验证改进算法的实用性，并对照文献[16]来比较重构结果，不含DG 重构结果比较如表1 所示。

表1 不含DG重构结果比较

由表1知，采用改进算法后，打开开关位置由初始状态变为7、9、14、32、37，有功网损降低到139.55 kW，与重构前相比降低了31.14%，最低节点电压由0.913 3 p.u.提升到0.941 5 p.u.；相比于文献[16]而言，在系统的有功网损的降低和最低节点电压的提升方面也具有一定的优势。

不含DG 重构前后电压曲线如图3 所示，利用改进算法对配电网重构，能有效提升节点电压水平，验证了改进算法的实用性。

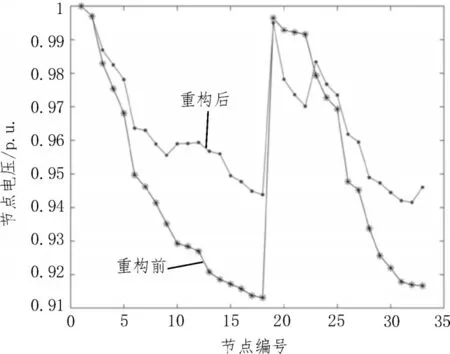
图3 不含DG重构前后电压曲线

虽然改进算法的优化结果与标准BPSO 一致，但是由图4 算法收敛曲线可以看出，标准BPSO 在搜寻的中后期容易陷入局部最优解，寻找全局最优解的能力较低。改进算法迭代至第9 次即可收敛至最优解，相比于标准BPSO而言，收敛速度有了一定的提升。

图4 算法收敛曲线

3.2 含有DG的重构

为了验证改进BPSO 在含有多种DG 的配电系统中是否实用，选取了四种DG，按照文献[17]中的参数以及并网位置进行设置，以有功网损和电压偏移作为目标函数进行重构研究，两者同样重要，取ω1=ω2=0.5。含DG 重构结果比较如表2 所示。

表2 含DG重构结果比较

分析表2 得出，配电网初始状态下的有功网损为202.65 kW，采用改进算法后，系统有功网损降低到98.93 kW，下降约51.18%；电压偏移从1.700 3 p.u.下降到了0.874 5 p.u.；最低节点电压由0.913 3 p.u.提升到了0.951 3 p.u.，对比文献[17]，采用改进算法对网络重构得到的网络性能指标具有一定的优势。

含DG 重构前后电压曲线如图5 所示。由图5 可以看出，在配电网中合适的位置接入DG 可以有效提升节点电压水平；采用改进BPSO 对含有DG 的配电网重构后，节点电压值进一步升高，有效提升了系统的电压水平。

图5 含DG重构前后电压曲线

4 结束语

将自适应比例选择策略和混沌搜索引入BPSO，通过判断粒子群中粒子的适应度来进一步更新粒子位置，该改进BPSO 用于配电网重构，算例表明所提方法可以有效提高算法效率，提升配电网性能，为后续研究更多目标配电网静态重构与动态重构提供了参考。