基于卷积神经网络的单机空战威胁评估

方 伟，张婷婷，余应福，谭凯文

（1.海军航空大学，山东烟台 264001；2.海战场信息感知与融合技术国家级实验教学中心，山东烟台 264001）

现代科技发展迅速，空中战场环境愈发复杂，作战模式趋向智能化，掌握对敌方战机进行快速准确地威胁评估对于我方战机的意义凸显[1]。空战威胁评估既为我机的火力分配和战时部署决策提供了理论依据[2-3]，也是空战态势感知的迫切需求[4]，是战机夺取作战主动权的关键因素[5]。

在现有的评估方法中，建模法[6-10]能够提高威胁评估的准确率，但由于计算时间受到模型复杂度和数据量的制约，实时性较差，不满足空战实际需求。数据法由于不需要建模而节省了大量时间，提高了计算效率，但评估准确率较低，不能为空战飞行员提供可靠的参考依据[11-12]。

针对以上两种方法存在的问题，文中提出一种基于卷积神经网络（CNN）的空战威胁评估模型[13-15]。首先基于作战任务背景对空战要素进行分析，提取主要威胁指标；然后构建威胁指数函数，以威胁要素为输入，输出威胁值；最后将威胁值量化后生成训练样本数据，利用卷积神经网络模型进行训练，实现对空战目标的及时准确的威胁评估。

1 威胁评估影响要素提取

对于单机空战，对敌方飞机的威胁评估主要考虑敌我双方的作战态势、机载武器装备的性能以及电子干扰等因素，该模型训练时设定敌我两机作战实力相当，空战能力威胁不纳入考虑。选取敌方飞机的飞行速度Vb(km/h)、我方飞机的飞行速度Vr(km/h)、相对飞行高度Hb(km)、相对距离R(km)和敌我两机航向角φb、φr六个因素[16-18]，计算威胁指数。

1.1 敌机速度

敌机速度指敌方飞机的飞行速度。速度越快，机动时间越短，越容易取得优势，对我方造成的威胁越大。速度威胁指数如下：

其中，Tv表示速度威胁指数，Vb为敌机飞行速度，Vr为我机飞行速度。当敌机速度小于我机速度的0.6 倍时，我机占据主要优势，当面临威胁时可以通过加速远离敌方攻击范围；当敌机速度在我机速度的0.6 倍和1.5 倍之间时，由于速度相差较小，敌机对我方威胁增大，很难仅凭加减速度夺取战场优势；当敌机速度大于我机速度1.5 倍时，敌方占据有利条件，我方飞机受到的威胁最大。

1.2 敌机高度

敌机高度指敌方飞机在垂直方向上与我方飞机的距离。在近距单机空战过程中，敌方飞机比我方飞机越高，对我方造成的威胁越大，若敌机在我机下方，则我机占据有利态势。高度威胁指数如下：

其中，TH表示高度威胁指数，Hb表示敌机高度，正值表示敌机在我机垂直上方，负值表示敌机在我机垂直下方。当敌机在我方飞机垂直上方超过5 000 km 距离时，对我机造成的威胁最大，敌机在我方飞机垂直下方超过5 000 km 距离时，对我机造成的威胁最小。

1.3 敌机距离

敌机距离指敌方飞机与我方飞机的连线距离。敌机与我机之间的距离越小，我机越容易进入敌机武器装备攻击范围，所得机动决策的时间越短，对我机的威胁越大；同理可知敌机距离越大，对我机的威胁越小。距离威胁指数如下：

其中，Tr表示距离威胁指数，R为敌机距离，Rb为敌机武器攻击距离，Rm为我机武器攻击距离，Rr为雷达最大跟踪距离。

1.4 敌机航向角

敌机航向角是指我机与敌机连线与敌我两机飞行轨迹方向的夹角。夹角越大，敌机对我机的威胁越大，夹角越小，敌机对我机的威胁越小。角度威胁指数如下：

其中，TA表示角度威胁指数，φb为敌机速度矢量方向与敌我两机连线的夹角，φr为我机速度矢量方向与敌我两机连线的夹角。根据公式可以看出，角度威胁指数随着两个夹角的增大而增大。

根据文献[19]可知，敌机的威胁值为角度威胁因子与距离威胁因子乘积后与其他因子加权得到，即：

其中，a1、a2、a3为各威胁因子的权重。文中取权重系数为a1=a2=1、a3=1.5。

2 威胁评估网络模型

2.1 威胁评估样本数据的构建

根据上述方法提取评估要素并计算相应威胁评估指标，然后，结合各威胁因子的权重计算得到每组数据中敌机对我机的威胁值，为了便于训练，减少训练时间，将所得威胁值进行量化，文中将空战威胁值分为三个等级，0、1、2 分别代表威胁程度较小、威胁程度中等、威胁程度较大。最后，以空战威胁要素为输入、量化后的威胁评估等级为输出，组成威胁评估模型样本数据。

2.2 卷积神经网络

在解决分类问题上，卷积神经网络具有较强的识别能力，它的学习机制与人工神经网络相同，由前向传递和后向传递组成，是在它的一个或多个层中使用卷积函数的一种神经网络。卷积神经网络由特征提取子系统和分类器子系统两部分组成。特征提取子系统是区别于卷积神经网络和其他特征提取方法的重要组成部分，特征提取子系统包括输入层、卷积层和池化层。卷积层主要用于提取输入数据的全部信息，实现特征提取功能；池化层用于压缩数据和特征信息，以减少数据的空间大小，特征提取子系统的输出作为卷积神经网络第二部分分类器子系统的输入，分类子系统包括全连接层。全连接层主要是将提取的特征加权之后进行非线性变换，然后映射到样本标记空间，实现分类功能。网络结构如图1所示，模型训练网络参数如表1 所示。

表1 模型训练网络参数

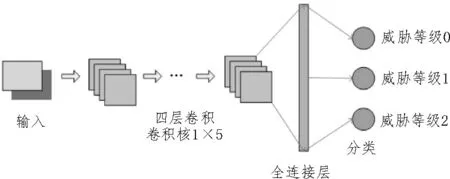
图1 卷积神经网络结构

2.3 威胁评估模型的构建

鉴于模型法准确度高却难以保证实时性、数据法实时性高却准确率不足的问题，文中提出一种基于卷积神经网络的单机空战威胁评估模型。首先根据威胁指数计算公式得到单机空战过程中每个时间点的敌机威胁值，然后将威胁值量化，生成样本数据，最后利用卷积神经网络进行训练，实现单机空战环境中对敌机的威胁评估。模型基本结构如图2 所示，基本步骤如下：

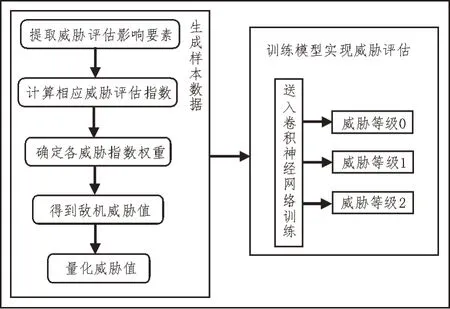
图2 单机空战威胁评估网络模型基本结构

步骤一：从空战数据中提取威胁评估影响要素；

步骤二：根据威胁指数计算公式计算相应威胁评估指数；

步骤三：确定各威胁指数权重；

步骤四：结合权重和评估指数计算得出敌机威胁值；

步骤五：将威胁值进行量化，分为0、1、2 三个等级；

步骤六：以威胁评估影响要素为输入，威胁评估等级为输出，生成训练样本数据；

步骤七：构建卷积神经网络，训练样本数据，实现单机空战情境下的威胁评估。

3 仿真分析

3.1 数据预处理

实验采用飞行模拟器进行真实单机对抗，采集作战过程中的数据信息，提取实验所需特征要素，主要包括敌方飞机的飞行速度Vb(km/h)、我方飞机的飞行速度Vr(km/h)、两机相对飞行高度Hb(km)、两机相对距离R(km) 和敌我两机航向角φb、φr六个要素，根据威胁指数计算公式得到每组对应的威胁值。其中，实验设定敌我双方飞机实力性能相当，即武器攻击范围相近，有：

将所得威胁值进行量化，具体标准如表2 所示，由此得到3 600 组输入为六项要素，输出为一项威胁等级的样本数据。

表2 威胁值量化标准

3.2 仿真实验

3.2.1 不同样本数量对模型的影响分析实验

将样本数据等比例分成训练集样本和测试集样本，设置模型参数为卷积层为四层、卷积核为1×5、迭代次数300 次、批样本数量为64，对模型进行训练。分别输入2 000 组、2 500 组和3 600 组样本数据进行实验，分析样本数量对模型性能的影响，选取损失函数和识别准确率作为衡量模型性能优劣的标准。图3 和图4 分别展示了样本数量为2 000 组时的损失函数和识别准确率，图5 和图6 分别展示了样本数量为2 500 组时的损失函数和识别准确率，图7 和图8 分别展示了样本数量为3 600 组时的损失函数和识别准确率。

图3 2 000组样本训练时的损失值

图4 2 000组样本训练时的识别准确率

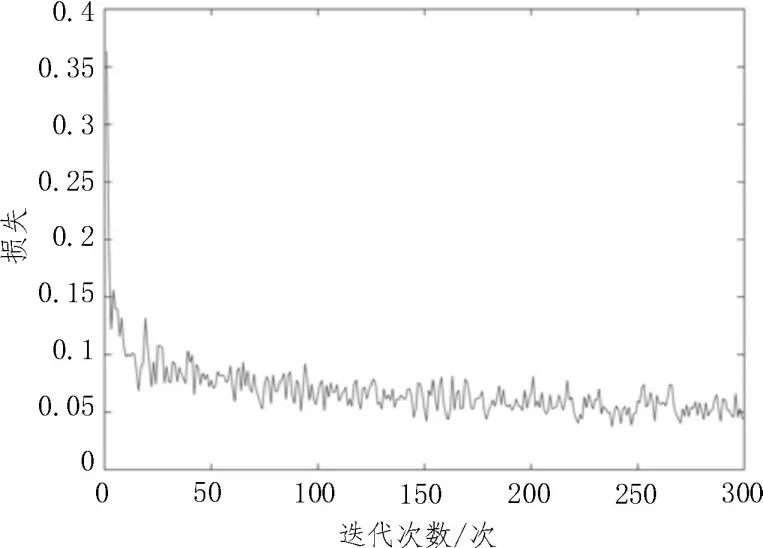
图5 2 500组样本训练时的损失值

图6 2 500组样本训练时的识别准确率

图7 3 600组样本训练时的损失值

图8 3 600组样本训练时的识别准确率

根据以上仿真实验可知，2 000组、2 500组、3 600组样本数据下模型训练的平均识别准确率分别为98.27%、98.50%、98.06%，说明该网络模型的识别准确率受样本数量影响较小，均能达到98%以上，对于处理大样本数据，同样具有较强的适用性。根据对比损失函数和识别准确率变化，可以看到模型训练过程中损失函数较小，该模型鲁棒性较好，且识别准确率变化幅度较小，说明该模型稳定性较好。

3.2.2 算法识别性能比较

将文中网络模型与标准化全连接残差网络模型[20]和基于加权动态云贝叶斯网络模型[21]进行仿真，对比结果如表3 所示。从表中可以看出，引入卷积神经网络对样本数据进行训练，有效提升了模型的特征提取能力，同时，将威胁值量化为三个威胁等级后，缩短了模型的训练时间，使该网络模型更加符合空中对抗的实时性要求，仿真对比表明，该网络模型在单机空战威胁评估上具有更高的识别准确率。

表3 网络模型训练结果对比

4 结论

文中针对传统的空战威胁评估方法中建模法准确率较高，但由于计算时间受到模型复杂度和数据量的制约，实时性较差；数据法提高了计算效率，但评估准确率较低的问题，提出了一种基于卷积神经网络的空战威胁评估模型。首先基于作战任务背景对空战要素进行分析，提取主要威胁指标；然后构建威胁指数函数，以威胁要素为输入，输出威胁值；最后将威胁值量化后生成训练样本数据，利用卷积神经网络模型进行训练，实现对空战目标的威胁评估。该模型能够在提高单机空战威胁评估准确率的同时，兼顾运算实时性，既满足了实战需求，为飞行员提供了机动决策的理论依据，也为夺取空中战场的胜利贡献了重要的作用。