“两步法”在初中物理浮力解题中的应用

任军文

(甘肃省静宁县贾河初级中学,甘肃 静宁 743411)

在初中物理学习中,浮力是一个重要的概念,由于浮力问题涉及的知识抽象,学生在解决此类问题时常常存在困惑[1].“两步法”的提出为解决这一问题提供了一个有力的工具,通过建立大等式方程,然后进行未知数的化解,我们可以通过已知条件和等式关系来求解未知条件,从而准确计算浮力.这种方法不仅能够帮助学生巩固对浮力原理的理解,也培养了学生的逻辑思维和解决问题的能力.

1 “两步法”解题概述

其次,未知化已知.把一个物理量一直拆分,拆分成相对应的物理量,目的是用到题目所给的已知量.如图1所示,F浮=ρ液gV排,其中V排是什么,得到上式F浮=ρ液gSh,其中Sh又是什么,最终上式F浮=ρ液gS0l0.

图1 浮力示意图

2 已知条件下的等量式“两步法”

浮力求解中,可以利用等量式的两步法进行化解.等量式的“两步法”是一种常用的求解问题的方法.在浮力求解中,我们可以先通过物体所受的重力、支持力以及浮力公式,先将受力分析的大等式列出,这是等量式的第一步.接下来,我们根据物体所受的浮力与重力之间的关系,将式中未知量进行代入化简,求解浮力.这是等量式的第二步[2].

等量式的两步法在浮力求解中非常实用,它能够帮助我们清晰地理解浮力与重力、支持力之间的关系,并通过逐步分析问题,一步一步地解决问题.这种求解方法的优点在于可以将复杂的问题分解成简单的步骤,提高求解的效率和准确性,在物理学和工程学中有着广泛的应用.

例1:如图2所示,小木块重F1, 浸没在密度为ρ0的液体中重F2, 求小木块密度.

图2 例1示意图

解析第一步:列大等式

求解方程可以得到:

代入密度求解方程得:

点评对于浮力问题,通常涉及的物体是浸入液体中的物体.已知量通常包括物体的体积、液体的密度、物体的密度或质量等.根据所涉及到的物体和液体之间的关系,我们可以列出相应的等量式.通过列等量式的两步法来求解浮力问题,可以帮助我们清晰地分析问题,将问题转化为数学计算,最终求解出问题的答案.

3 部分条件未知情况下的差量式“两步法”

在浮力求解中,有时候会遇到一些条件未知的情况,这时可以利用差量式的两步法进行化解.差量式与等量式的两步法基本一致,主要区别在于差量式中的部分变量需要通过不同状态下的“差量”进行变量构造.

首先,我们需要明确浮力方程的不变性.根据浮力原理,浮力与物体所排开的液体的重量相等,即所受浮力等于物体所排开的液体的重力,这个等式在任何状态下都成立[3].其次,根据差量式的思路,我们可以建立差量方程.差量方程通过考虑物体从一个状态到另一个状态的变化量来表示未知条件的关系.差量方程可以表示物体在两个状态之间质量差的增量与浮力差的关系.然后,我们可以通过差量方程来构造其他未知条件的变量.

通过差量方程,我们可以建立物体在不同状态下的质量和浮力之间的关系,从而通过已知条件和差量方程来求解未知条件,实现浮力的准确计算.

例2如图3,一根圆柱体可燃塑料棒, 下方挂有铁块(长度、体积可忽略不计), 直立在密度为ρ0的液体中,点燃该塑料棒, 它的长度由l1减少到l2,在接触水面后熄灭, 假设塑料棒密度为ρ1,求最开始塑料棒露出液面的长度.

图3 可燃塑料棒浮力分析示意图

解析第一步:列大等式(差量式和结果式)

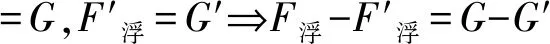
ΔF浮=ΔG

第二步:未知化已知

ρ0gΔV排=Δmg=ρ1ΔVg

设蜡烛底面积为S,露出的长度为l3

ρ0gSΔh=ρ1SΔhg

ρ0gS[l1-l3-l2]=ρ1S(l1-l2)g

化简可得

点评本题中因含有未知量“塑料棒的总长度”,并且随着塑料棒的燃烧,塑料棒露出水面的过程其实是一个动态的过程,确实会增加一定的难度.但在实际解题过程中,只需要利用原始方程进行细心推导,便可得到最后的结果.比如题中利用差量法,将浮力和重力的关系式变成其变化量的关系式,进而将塑料棒的长度进行假设,利用体积与重力的关系,代入求解.

在解决动态过程的浮力问题时,需要注意对每个时刻的情况进行分析,考虑时间、位置等因素.尽管解决涉及未知量和动态过程的浮力问题可能会增加一定的难度,但只需要利用原始方程进行仔细推导,仍然可以得到最后的结果.通过综合考虑液体的密度、物体的密度、物体的体积和液面的变化等因素,我们可以将问题转化为数学计算,最终求解出问题的答案.

4 “两步法”在浮力分类讨论题目中的应用

浮力求解中,我们偶尔会遇到一些需要分情况讨论的复杂问题.这些问题需要我们根据物体的状态和条件的不同,采用不同的方法来解决.这种情况下,我们依然可以使用浮力求解的“两步法”,以确保我们得到准确的结果.例如,当物体完全浸没在液体中时,即物体的体积大于或等于液体的体积时,我们可以直接计算出浮力的大小.然而,当物体只有部分浸没在液体中时,我们就需要分情况讨论.对于部分浸没的物体,我们可以首先计算物体浸没的部分的体积,并根据这一体积计算出浸没部分受到的浮力.然后,我们再计算物体未浸没的部分受到的浮力,并将两部分浮力相加,得到这个特殊情况下的总浮力.

例3如图4,有一个容器的容积为V, 一个正方体物块的密度为ρ1, 体积为V1,在保证液体不流出容器的情况下,最多可以倒入密度为ρ0的液体的最大质量mmax是多少?

图4 液体与物体密度分类讨论

解析:由于题目中未说明ρ0和ρ1的大小关系,因此需要分情况讨论.

第一种情况:当物体密度大于液体时, 物体沉底,此时:mmax=ρ0Vmax=ρ0(V-V1)

第二种情况:当物体密度小于等于液体时, 物体漂浮/悬浮,此时:mmax=ρ0Vmax=ρ0(V-V排)

在上式中,V排不会求,因此可列大等式F浮=G

未知化已知得到:ρ0gV排=m1g=ρ1V1g

点评在浮力分类讨论题中,常常需要根据物体的密度与液体的密度之间的大小关系来判断物体的浮力情况,进而分类讨论解决问题.这时可以运用两步法来帮助解决问题.在实际情况中,学生比较容易忽略其中一种情况.但通过两步法解题,学生能通过式子的判断发现自己的疏漏.如当学生看到(V-V1)或者(ρ1-ρ0)时,会自然地进行比较,然后想到分类讨论,从而减少疏漏.

通过文章所介绍的“列大等式、未知化已知”两步法,我们可以更加有效地解决初中物理中的浮力问题.文章通过具体的浮力问题示例,详细讲解了这一方法的具体操作步骤和思路,提出了几个需要注意的重点和技巧.两步法不仅可以用于初中物理中的浮力问题,还可以应用于一些涉及力学和物理学知识的实际问题.此外,这一方法还可以帮助我们更好地理解浮力所涉及的基本原理和应用场景,掌握更加有效的解题思路和方法,进而在更高层次上理解和应用浮力理论.