计算机自适应测验分阶段应用能力估计方法的模拟分析

[摘要]概述计算机自适应测验的极大似然估计方法、极大后验估计方法、期望后验估计方法及其变式以及优缺点。在CAT测试初始、中间、最终阶段分别设计不同的能力估计方法并进行模拟研究。结果显示，CAT的初始、中间、最终阶段同时使用MLE或Biweight、EAPE-U（-4，4）方法，各个能力水平的被试均能被准确测量；CAT的初始、中间、最终阶段中使用EAPE-N（0，1）方法或EAPE-N（0，2）方法，则高能力被试出现一定程度低估现象，低能力被试出现一定程度高估现象，而且所有被试的能力估计值呈现向能力量尺的中间靠拢的趋势。

[关键词]CAT；极大似然估计；极大后验估计：期望后验估计

[中图分类号]G424.74[文献标识码]A

[文章编号]1673—1654（2023）02—056—012

项目基金本文为国家社会科学基金后期资助项目（编号：21FJKB021），江西省社会科学研究规划项目（计算机化自适应测验技术发展分析与实测应用，编号19JY02）的研究成果。

在计算机自适应测验（computerized adaptive testing，CAT）的测试过程中，每一道试题在被试作答后，需要进行即时能力估计；在CAT测验终止时，需要进行最终能力估计。能力估计是CAT测验流程与测量技术的主要环节之一，以往研究者已提出了多种能力估计方法。张心和涂冬波概述了CAT常见的几种能力估计方法，包括极大似然估计方法（maximum likelihood estimation，MLE）、极大后验估计方法（expected a-posteriori estimation，EAPE）和期望后验估计方法（maximum-a-posteriori estimation，MAPE）的基本原理及特点[1]。Wang概述了多位研究者对MLE、Owen方法、MAPE这几种能力估计方法在纸笔测验、CAT测验情境下的比较研究[2]；通过CAT模拟研究比较分析了MLE、Owen方法、EAPE、MAPE这四种能力估计方法，对其优缺点进行了评论[3]。本文将在张心、Wang等的研究基础上补充论述，重点论述MLE、EAPE、MAPE这三种能力估计方法的变式，概述以往研究者在CAT中分阶段应用能力估计方法的思路。同时，设计模拟研究，分阶段应用于CAT能力估计，对以上方法及其变式在CAT测试中的测量性能进行比较分析。

一、CAT常用能力估计方法及其变式

（一）MLE方法及其变式

Birnbaum最早在两参数、三参数Logistic模型下采用极大似然估计方法来估计被试能力，这是IRT研究中被试能力估计的主要方法之一[4]。以往研究发现，MLE方法是能力估计方法中偏差最小的[2]。但是MLE方法也存在不足：当被试作答全对或者全错时，被试能力估计的似然方程会无法估计，这将使得CAT初始阶段只能选题让被试作答。李佳等提出了增加极端难度试题的改进MLE方法，即NMLE方法，增加一道区分度大、难度低的试题，且假设被试答对；增加一道试题区分度大、难度大的试题，且假设被试答错[5]。李佳等的研究结果显示，通过增加两道试题，能够改进MLE方法无法处理被试作答全对或全错的情况，以及能力估计不收敛的问题。

（二）MAPE方法及其變式

MAPE方法及其变式实际上是在MLE方法的基础上增加被试能力分布密度函数信息。Samejima将后验分布f （θ）引入了MLE被试能力估计公式[11]，将先验概率密度乘以似然函数构建后验分布并求极大值，因而被称为极大后验估计。MAPE本质上是MLE的进一步发展，是在MLE估计公式的基础上结合贝叶斯后验分布而形成的能力估计方法。Wang初步论述了MAPE方法的优缺点[3]。MAPE方法的优点是，在许多测验情境下，被试群体能力量表的中段人数较多，而处于能力量表两端的人数较少，MAPE可以利用后验信息将被试能力估计值向能力量表的中部“聚集”，从而整体上减小了对每个被试的估计误差。MAPE方法的缺点是，由于MAPE方法本质上是MLE方法的改进，MLE方法存在的缺点，MAPE方法可能都存在；而且，MAPE方法出现估计向先验均值回归的现象，可能会造成处于能力量尺两端的被试在能力估计时出现偏差。

以往研究者在MAPE方法的基础上，提出了多个变式，包括：Wang，et al.在MAPE方法中加入了Beta先验分布参数α、β，以及设置u、l参数，从而提出了无偏MAPE方法（EU-MAPE方法）[12]；Sun等提出了MAPE的加权变式，即WMAPE方法[13]；Magis等提出BME方法使用Jeffreys先验分布，形成MAPE的变式方法即Jeffreys模型方法[14]。以上几个MAPE方法的变式在理论与实践研究中应用较少。

（三）EAPE方法及其变式

Bock和Mislevy阐述了EAPE方法具有多方面的优点[10]：（1）EAPE方法在能力估计时不需进行迭代计算，计算过程简洁；（2）EAPE方法不依赖于被试的先验信息分布假设，使得EAPE方法能够依据测验经验，或实践需要来进行估计；（3）对被试全对或全错的作答得分情况也能进行能力估计，在CAT初始阶段被试作答试题量很少时，可以使用EAPE方法得到相对准确的估计等。不过，在Bock和Mislevy的CAT模拟研究结果显示，EAPE方法对高能力被试会出现一定程度的低估，而低能力被试出现一定程度的高估[16]。

EAPE方法的后验分布不使用正态分布，使用某一指定后验分布，就成为EAPE方法的变式方法。Rulison等、简小珠的CAT研究中使用EAPE-N（0，2）方法（后验分布均值为0，方差为2的EAPE方法）、EAPE-N（0，1）方法、EAPE-N（0，0.5）方法[17-18]，由模拟结果可得，在CAT测试的后期阶段，EAPE- N（0，2）方法的能力估计准确性要优于EAPE-N（0，1）方法、EAPE- N（0，0.5）方法。一些研究者还使用了EAPE方法的其他变式，如Barrada等在分析多重曝光率控制的CAT模拟研究中，使用了EAPE-U（-4，4）能力估计方法，即后验分布为均匀分布U（-4，4）[19]；Chen在研究中使用能力估计方法EAPE-U（-4，4）、EAPE负偏态分布的方法[20]。

二、CAT分阶段应用能力估计方法概述

近年来，一些研究者提出了能力估计方法的分阶段应用思路，即在CAT的不同阶段、或在不同测验情境时使用不同能力估计方法，以改进或克服使用单一能力估计方法时的缺点与不足。CAT初始阶段试题信息和被试作答信息都很少，此时试题的选择往往采取试探性选择方式，第一个试题往往是难度适中的试题，或者使用试题包方法，前三道试题均选择难度适中的试题，待被试完成3道试题后再进行被试能力估计。目前，已有不少研究者进行了这方面的尝试研究。例如，朱隆尹等提出将CAT测试分为前后两个阶段，即初步能力探查阶段（试题数量为5题左右）和精确估计阶段[21]，并由模拟研究显示，能力估计方法在这两个不同的测试阶段，其能力估计精度不同；张心的CAT模拟研究中，在前期和中期采用EAPE方法，后期采用WLE方法[22]，并由模拟结果发现，使用综合能力估计方法的偏差Bias小于EAPE方法的偏差，而且综合能力估计方法的RMSE与单纯使用EAPE方法时差不多；蔡艳在研究中提出了改进的MLE法（简记为R-MLE）[23]，将EAPE方法与MLE方法相结合，即在CAT测试过程中，如果被试得满分或0分则采用EAPE进行估计，否则采用MLE估计，这样，从CAT的第2题开始就实现了对被试进行能力估计，并进行自适应选题，提高了CAT测试的效率，这种新方法是在弥补MLE方法不能估计“全得满分或0分的被试”这一不足的基础上提出来的。

在CAT测试的中间阶段，van der Linden等认为，试题选择策略与能力估计方法应该可以自由组合，而不是局限于早期CAT研究者的“自然”搭配。早期的自然搭配就是：MLE估计方法与最大项目信息量选题策略；Owen贝叶斯能力估计方法与基于后验分布的项目选择。

在CAT测试的最终能力阶段，van der Linden等认为，最终的能力估计应该具有最优的统计特性，此时，最终能力估计方法的主要功能不再是根据被试能力估计值来选择下一道项目，而是以可能的最佳形式为考生提供一个有意义的能力估计与评价。

总之，以往研究者认为，为了更好地适应CAT测试过程，在不同的阶段应该使用不同的能力估计方法。如前所述，朱隆尹等、张心、蔡艷等研究者分阶段使用了不同的能力估计方法[21-23]，但是，这些研究对CAT阶段的划分，以及对能力估计方法比较均不够细化。本文根据CAT测试过程的特点，在CAT分三个阶段采用不同能力的估计方法，并对这些方法及其变式进行比较，实现对各个能力层次被试的估计。

三、CAT分阶段应用能力估计方法的模拟研究

（一）研究设计

题库模拟与被试选择。模拟生成一个理想的题库，题库题量为3000题，试题的区分度参数log（a）服从正态分布N（0，1），试题难度b参数服从U[-3，+3]。被试群体的模拟设计：在能力区间[-3，+3]之间，选取-2.7，-2.4，-2.1…. 2.1，2.4，2.7共19个被试能力水平作为CAT模拟的被试能力真值，以代表不同能力水平的被试。

测验起点与测验长度：在两级记分两参数Logistic模型下，CAT测试起点从能力量尺的中间0.0开始。CAT模拟测验的长度为30题，即被试完成30题则终止测验。

选题策略：主要依据最大信息量选题策略，以往对试题曝光率控制的CAT模拟研究表明，如果加入了复杂的选题策略算法，试题曝光率往往使得所有被试的被试能力估计值的测量精度下降。所以以往的有些CAT模拟研究中，为了排除试题曝光率控制所带来的干扰，往往都没有加入试题曝光率控制。同样地，本文为了排除试题曝光率对测验精度的影响与干扰，在CAT测验模拟过程中没有加入试题曝光率控制算法。

能力估计方法：在CAT三个阶段采用不同能力估计方法。这里对van der Linder CAT三个阶段进行了具体的描述与定义，具体如下：初始能力估计阶段（初始阶段）是指CAT测试过程中第1题至第3题，中间即时估计阶段（中间阶段）是指CAT测试过程中从第4题开始至测验最后一道试题，最终能力估计阶段（最终阶段）是指CAT测试结束时，此时进行最后的能力估计与评价。

本研究所定义的CAT测试全过程包括CAT初始阶段、中间阶段，从第一题至最后一题，但不包括最终能力估计阶段。

CAT测试的全过程，共设计8种CAT模拟情境：

1.测试全过程使用MLE方法，而且在初始阶段前几题时，如果被试全部答对则赋予最大值+3，全部答错则赋予最小值-3。如果被试能力估计值收敛值大于3，则赋予+3；如果收敛于小于-3，则赋予-3；

2.测试全过程使用Biweight方法，在初始阶段被试能力估计时的设定同第1种情境；

3.测试全过程使用EAPE-N（0，1）方法；

4.测试全过程使用EAPE-U（-4，+4）方法；

5.测试全过程中分段使用EAME方法的多个变式，即：前15题使用EAPE-N（0，1）方法，最后15题使用EAPE-U（-4，+4）方法；

6.测试全过程中分段使用能力估计方法，初始阶段第1至3题使用EAPE-N（0，1）方法，中间阶段第4至30题使用EAPE-U（-4，+4）方法；

7.测试全过程中分段使用能力估计方法，初始阶段第1至3题使用EAPE-N（0，1）方法，中间阶段第4至30题使用MLE方法；

8.测试全过程中分段使用能力估计方法，初始阶段第1至3题使用EAPE-U（-4，+4）方法，中间阶段第4至30题使用MLE方法。

第6、7、8CAT测试情境的过程设计，本质上是增加CAT初始阶段（第1至3题）的设计，而且第1-3题使用EAPE-N（0，1）方法、EAPE-U（-4，+4）方法，是一些研究者认为，在CAT测试初始阶段，由于作答试题数量少，被试作答信息少，使用MLE方法会出现能力估计不收敛或者无解的情况，包括van der Linden等也提出在CAT初始阶段使用EAPE方法。

最终能力估计阶段设计：在以上8种CAT测试过程的模拟情境下，当每一个被试在每一次模拟测验结束时，根据被试在每一次模拟测验作答得分情况分别使用5种能力估计方法进行估计。这5种能力估计方法为：MLE方法、MLE-Biweight方法和EAPE-N（0，1）方法、EAPE-N（0，2）方法、EAPE-U（-4，+4）方法。由于MAPE方法的测量精确性不如MLE方法，这里的模拟研究设计不使用MAPE方法及其变式。

评价指标：在每一个测验情境下，19名被试中的每一名被试都进行5000次CAT测验模拟作答过程。在每个测验情境完成模拟后，分析每个被试的模拟返真性能Bias、RMSE、测验SE。

（二）结果与分析

1.测试全过程使用MLE方法的模拟结果与分析

测验全过程使用MLE方法，完成测验模拟后，使用五种能力估计方法进行估计，对19名被试的模拟测验结果的评价指标进行整理分析，详见表1和图1、图2。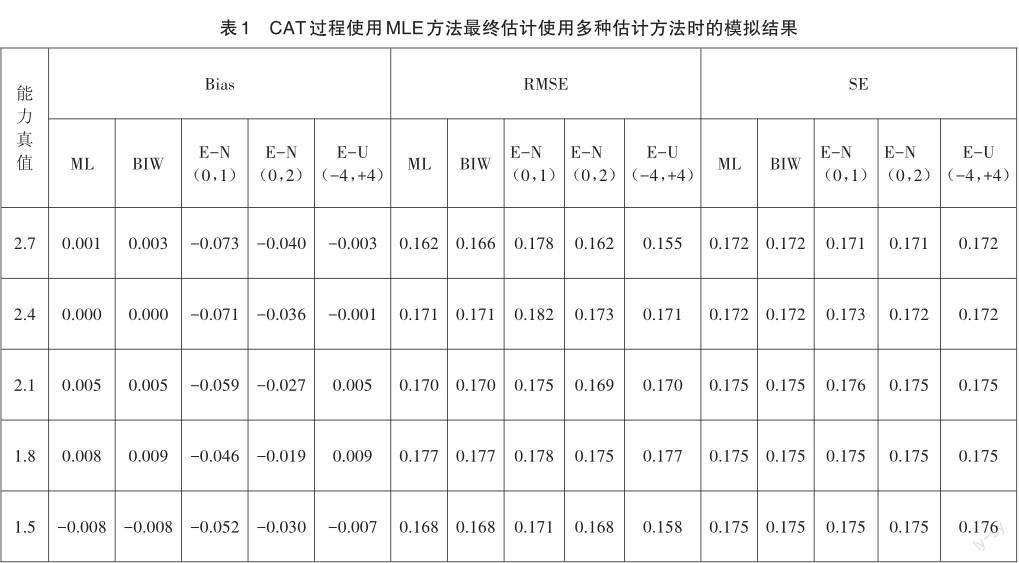

首先，由表1和图1中各个被试的Bias可知，最终能力估计方法使用MLE、Biweight、EAPE-U（-4，4）方法时，19名被试的偏差在这三种方法上的偏差值的大小几乎相同，而且都很小，偏差Bias都在0.02以内，说明这三种能力估计方法的测量属性较好，能够对各个能力层次水平的被试做出准确的测量。

其次，分析图1中当最终能力估计方法为EAPE-N（0，1）、EAPE-N（0，2）方法时，这19名被试之间的偏差出现有规律的变化趋势。在被试能力真值接近0时，其Bias值很小；而被试能力真值为+3或-3时，其Bias值相对较大。在图1的左端，从中间能力真值为0的被试至左端能力真值为-2.7的被试，Bias绝对值随着被试能力真值减小而逐渐增大，即测量准确性随之越差；在图1的右端，从中间能力真值为0的被试至右端的能力真值为2.7的被试，Bias随着被试能力真值增大而逐渐增大，即测量准确性随之越差。这表明，EAPE-N（0，1）、EAPE-N（0，2）方法在能力量尺两端的测量准确性较差。为什么使用EAPE-N（0，1）方法、EAPE-N（0，2）方法时，中等能力被试的模拟返真性能要优于高、低能力被试？这主要是EAPE-N（0，1）方法、EAPE-N（0，2）方法都是假设被试的能力分布为正态分布，在中等能力区间的密度大，因此，被试能力估计值存在“向中间靠拢”的倾向，即高、低能力被试的能力估计值容易向能力分布的平均值靠拢，因而使得被试能力估计值与被试能力真值产生较大偏差，即Bias和RMSE相对较大；而且这些高能力或低能力被试能力真值距离平均值0.0越远，Bias和RMSE则越大。Mislevy等在CAT模拟研究中也得到了类似的结论，即在EAPE方法下，被试能力估计值容易向平均值靠拢[6]。

再次，横向对比表1中的EAPE-N（0，1）、EAPEN（0，2）、EAPE-U（-4，4）三种方法下的Bias、RMSE值，发现这三种方法在低能力被试（以-2.1至-2.7为代表）和高能力被试（以2.1至2.7为代表）的Bias、RMSE值的绝对值依次减小，特别是EAPE-U（-4，4）方法下高能力、低能力被试Bias、RMSE的大小与其他能力水平被试的Bias、RMSE一样，没有EAPE-N（0，1）方法时被试能力估计值向能力量尺中间靠拢的现象。因此，在使用EPAE方法时，应该使用后验分布为均匀分布的EAPE方法。

第三，由表1可知，从能力真值-2.7至2.7的19名被试，这五种能力估计方法的RMSE值都在0.170左右，而五种方法的总体RMSE为0.173-0.176之间。总体RMSE这一数值，与前人Wang等（1998）研究的表2中的MLE方法，测验长度30时RMSE值为0.17，基本一致。

最后，表1中RMSE指标与测验SE指标值的大小基本上相同，RMSE、测验SE均反映测验的随机误差的大小。从前人研究Wang等（1998）以及本文的模擬研究结果中都可以发现，RMSE指标与测验SE指标值的大小很接近或相等，说明在各个能力水平被试的测量精度都比较一致。

2.第2～8测验情境下的模拟研究结果与分析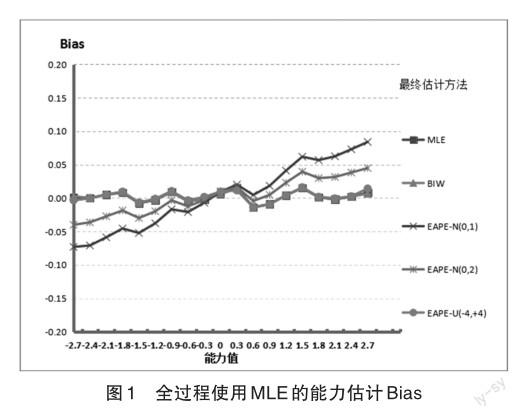

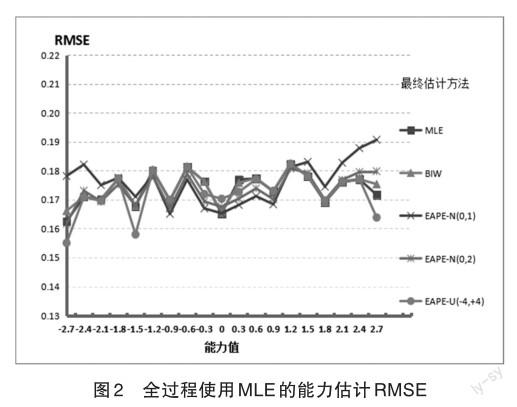
在第2～8种测验情境下进行CAT测验模拟，并对测验模拟结果进行整理分析，得到Bias、RMSE、测验SE评价指标。第2～8种测验情境的Bias情况如图3至图9所示。在各个测验情境下的RMSE指标与Bias指标的变化趋势近似一致：Bias偏大，则RMSE偏大；Bias偏小，则RMSE偏小；因而以下RMSE指标不用图形表示。而且，由于测验SE指标在各个能力层次水平的变化很小，如同表1的SE一样，因而这里就不再用图形展示。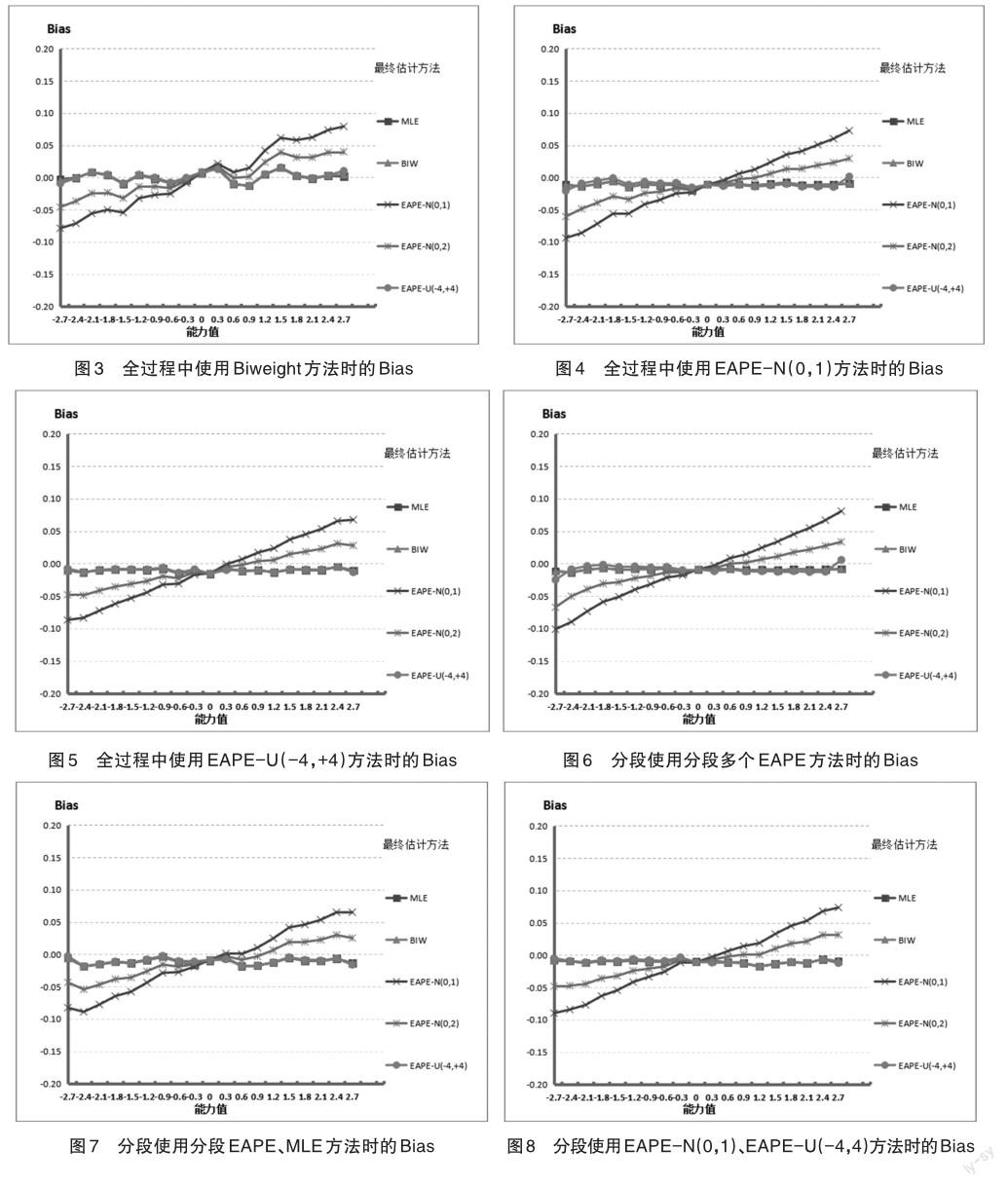

首先，将图3、图5与图1的情况放在一起进行分析，测验的过程中使用Biweight方法、EAPE-U（-4，+4）方法时的Bias，与全过程使用MLE时的Bias的数值情况在各个层次被试能力水平上的数值大小基本一致，可以认为在CAT测试中，过程中能力估计使用MLE方法、Biweight方法、EAPE-U（-4，+ 4）方法，且最终能力估计方法也是这三种方法时，对被试能力估计的测量误差是基本一致的，偏差接近于0。从表1的数值看，最终能力估计方法为MLE时，各个被试的Bias偏差小于0.015，这一数值与前人Wang等研究的表2中能力估计方法为MLE方法且测验长度30时的Bias值0.016基本一致[3]。这说明在MLE、Biweight、EAPE-U（-4，4）方法下，CAT能对各个能力水平的被试实现准确的测量，即MLE、Biweight、EAPE-U（-4，4）对各个层次水平的被试都能实现无偏估计，换句话说，MLE、Biweight、EAPE-U（-4，4）方法是被试能力估计的无偏估计方法，这可視为以上能力估计方法应用于被试能力测量的一个优点。

其次，在图4中当CAT测试过程、最终阶段的能力估计方法都使用EAPE-N（0，1）方法时，此时高能力被试和低能力被试的Bias（或Bias绝对值），与其他能力水平的被试相比，相对较大，而且比图1中的最终能力估计方法使用EAPE-N（0，1）方法时，对应的高能力被试和低能力被试的Bias（或Bias绝对值）、RMSE还要大一些。也就是说，在CAT测试过程和最终能力估计阶段时都使用EAPE-N（0，1）方法，高能力被试和低能力被试段的Bias（或Bias绝对值）、RMSE比较大，而中间能力被试的Bias（或Bias绝对值）、RMSE比较小。这意味着，中间阶段和最终能力估计方法使用EAPE-N（0，1）方法有利于中等能力被试的测量，而不利于高能力被试或低能力被试的准确测量。这里图4的研究结果，与Wang等研究文献的图3中EAPE的Bias值的曲线变化趋势几乎是一致的。然而，本文图4的EAPE-N（0，1）方法中高能力、低能力被试的Bias值或绝对值，要小于Wang等的Bias值，这是由于Wang等模拟研究中题库试题难度参数使用正态分布，而本文的题库试题难度参数采取均匀分布，使得高能力、低能力被试在模拟测验时有足够难度合适的试题来进行测试，因而测量的准确性要高一些。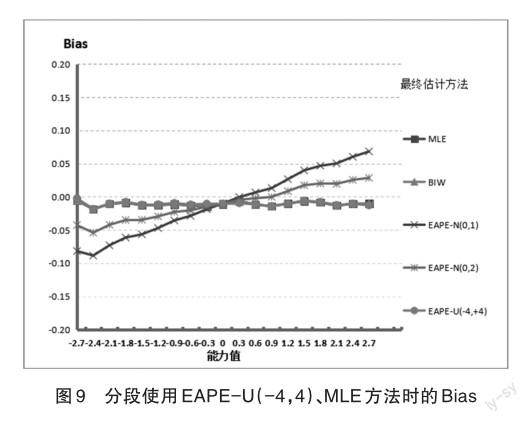

再次，将图6、图7、图8与图1对比分析，发现图 6、图7、图8中在CAT初始阶段、中间阶段使用了EAPE-N（0，1）方法的变式，而最终能力估计方法使用EAPE-N（0，1）方法、EAPE-N（0，2）方法时的偏差Bias，与图1中相对应的EAPE-N（0，1）方法、EAPEN（0，2）方法时的偏差Bias要相对大一些，也就是说，在CAT测试过程的初始阶段使用了EAPE-N（0，1）方法，会对高能力被试、低能力被试的准确测量产生较大的影响，使得高能力被试、低能力被试的估计值向能力量尺中间聚拢。同时，分析图7、图8中在CAT初始阶段前3题使用了EAPE-N（0，1）方法，而最终能力估计方法MLE方法、Biweight方法、EAPEU（-4，4）方法时的偏差Bias几乎接近于0，这与图1基本一致，说明最终能力估计使用MLE方法、Biweight方法、EAPE-U（-4，4）方法有助于纠正在CAT初始阶段使用EAPE-N（0，1）方法造成的偏差影响。

最后，分析图9并与图1对比，发现图9与图1在各个能力估计方法上的偏差Bias大小几乎一致，几乎都是接近于0；而且，各个层次、能力水平的Bias的大小非常一致。在模拟过程中，具体跟踪记录分析所有被试在使用MLE方法时的每一步作答情况，均没有发现MLE在能力估计时无解或不收敛的情况，也没有发现MLE估计时出现多个极大值的情况。

总之，在CAT测试初始阶段、中间阶段和最终估计阶段，MLE方法是能力估计方法中Bias、RMSE最小的，Bias几乎接近0，即对各个层次被试能力水平的测量都是相对准确的；同时Biweight、EAPE-U（-4，4）方法的测量准确性与MLE方法几乎一致。以往研究中也曾得出同样的结论，Samejima（1993）通过假设推理[26]，推论了MLE的偏差函数的性质，假定测验所有试题的试题难度与能力估计值相当时，偏差为0；当被试能力水平比测验的平均项目难度水平高，则偏差是正的；当能力水平低于平均项目难度水平，则偏差是负值。其他研究者通过纸笔测验模拟，或者在CAT模拟测验的研究结果也可得到同样的结论。Wang等（1998）认为在适应性测验形式下，被选择的试题难度总是与被试能力水平相匹配，测验平均难度与被试能力水平的差距会逐渐接近0，因此MLE是一种渐进无偏的能力估计方法[3]。

四、结论

在CAT测试全过程中，被试能力估计方法使用MLE、Biweight、EAPE-U（-4，4）方法，而且最终阶段的能力估计方法为MLE、Biweight、EAPE-U（-4，4）方法时，此时这三种能力估计方法的Bias很小，几乎接近0，这说明在MLE、Biweight、EAPE-U（-4，4）方法下，CAT能对各个能力水平的被试均实现准确的测量，这可以认为是计算机化适应性测验应用于被试能力测量的一个重要理论依据之一。也就是说，MLE、Biweight、EAPE-U（-4，4）这三种方法是对被试能力估计的无偏估计。此研究结论与前人研究认为MLE方法是对被试能力无偏估计的这一观点一致。

CAT测试全过程中，被试能力估计方法使用EAPE-N（0，1）方法或者EAPE-N（0，2）方法，而且最终能力估计方法为EAPE-N（0，1）方法或者EAPE-N（0，2）方法时，高能力被试会出现一定程度低估现象，低能力被试会出现一定程度高估现象，即高能力、低能力被试的能力估计值向中间靠拢的现象。此研究结论与前人研究观点是一致的。而且，只要CAT初始阶段中使用了EAPE-N（0，1）方法，就会使得高能力、低能力被试的Bias、RMSE相对变大。因此，CAT测试的初始阶段、中间阶段、最终阶段都不建议使用EAPE-N（0，1）方法或者EAPE-N（0，2）方法。总之，根据CAT模拟研究结果，建议在CAT测试过程的初始阶段、中间阶段、最终阶段时，使用MLE、Biweight、EAPE-U（-4，4）这三种方法中的一种，或者将这三种方法组合应用。

参考文献：

[1]张心，涂冬波.计算机化自适应测验中几种常用能力估计方法的特性与评价[J].中国考试，2014，21（5）：18-25.

[2] Wang T. The Precision of Ability Estimation Methods in Computerized Adaptive Testing [D]. University of Iowa，1995.

[3] Wang T，Vispoel W P. Properties of Ability Estimation Methods in Computerized Adaptive Testing [J]. Jorunal of Educational Measurement， 1998，35：109-135.

[4] Birnbaum A. Some Latent Ability Models and their Use in Inferring an Examinees Ability [M] // F. M. Lord，M R. Novick. Statistical Theories of Mental Test Scores. Reading，MA：AddisonWesley. 1968：392-479.

[5]李佳，丁樹良.计算机化自适应测验中能力估计新方法[J].江西师范大学学报（自然科学版），2019，43（2）：142-146.

[6] Mislevy R J，Bock R D. Biweight Estimates of Latent Ability[J]. Educational & Psychological Measurement，1982，42（3）：725-737.

[7] Warm T A. Weighted Likelihood Estimation of Ability in Item Response Theory [J]. Psychometrika，1989，54（3）：427-450.

[8] Schuster C，Yuan K. Robust Estimation of Latent Ability in Item Response Models [J]. Journal Of Educational And Behavioral Statistics，2011，36（6）：720-735.

[9] Jones D H. Redescending M-Type Estimators of Latent Ability[R]. Program Statistics Research，Technical Report No. 82-30，1982.

[10]简小珠，戴海琦.“CAT初始作答影响最终成绩”的模拟分析与纠正[J].心理学探新，2016，36（03）：276-280.

[11] Samejima F. Estimation of Latent Ability Using a Response Pattern of Graded Scores [J]. Psychometrik，1969，34：1-97.

[12] Wang，T.，Hanson，Bradley，A.，Lau，C. Reducing Bias in CAT TraitEstimation：AComparisonofApproaches[J].Applied Psychological Measurement，1999，23：263-278.

[13] Sun，S.，Tao，J.，Chang，H. H.，et al. Weighted Maximum-aPosterioriEstimationinTestsComposedofDichotomousand Polytomous Items [J]. Applied Psychological Measurement，2012，36（5）：399-419.

[14] Magis，D.，& Ra？che，G. On the Relationships Between Jeffreys Model and Weighted Likelihood Estimation of Ability Under Logistic IRT Models [J]. Psychometrika，2012，77（1）：163-169.

[15] Bock RD，Aitkin M. Marginal MaximumLikelihood Estimation of Item Parameters：Application of an EM Algorithm [J]. Psychometrika，1981，46（4）：443-459.

[16] Bock R D，Mislevy R J. Adaptive EAP Estimation of Ability inaMicrocomputerEnvironment[J].AppliedPsychological Measurement，1982，6（4）：431-444.

[17] Rulison K L，Loken E. Ive Fallen and I Cant Get Up：Can High Ability Students Recover From Early Mistakes in CAT？ [J]. Applied Psychological Measurement，2009，33（2）：83-101.

[18]简小珠. IRT模型中c、γ参数对被试能力高估和低估现象的纠正[D].广东广州：华南师范大学，2011.

[19] Barrada J R，Abad F J，Veldkamp B P. Comparison of Methods for Controlling Maximum Exposure Rates in Computerized Adaptive Testing [J]. Methodology，2009，21：313-320.

[20] Chen S. The Comparison of Maximum Likelihood Estimation and Expected a Posteriori in CAT Using the Graded Response Model[J].國教学报（中国台湾），1996，19：339-371.

[21]朱隆尹，丁树良.CAT能力估计方法的比较研究[J].江西师范大学学报（自然科学版），2007，31（3）：302-305.

[22]张心.CAT常用能力估计方法比较及其优化：能力综合估计方法开发[D].江西南昌：江西师范大学，2014.

[23]蔡艳.CAT中能力参数估计方法的改进：R-MLE估计法[J].心理学探新，2016，36（1）：92-96.

[24] van der Linden W J，Pashley P J. Item Selection and Ability Estimation in Adaptive Testing [M] // van der Linden W J，Glas C A W. Elements of Adaptive Testing. Springer New York，2010.

[25] Dodd，B.，G. The Effect of Item Selection Procedure and Step Size on Computerized Adaptive Attitude Measurement Using the Rating Scale Model [J]. Applied Psychological Measurement，1990，14（4）：355-366.

[26] Samejima F. The Bias Function of the Maximum Likelihood EstimateofAbilityfortheDichotomousResponseLevel[J]. Psychometrika，1993，58（2）：195-209.

Comparison between Ability Estimation Methods under Computerized Adaptive Testing

Jian Xiaozhu

Department of Education，Guangxi Normal University，School of Education，Jinggangshan University，Jian，Jiangxi，343000

Abstract：This paper summarizes three main types of computerized adaptive testing（CAT）ability estimation methods，namely，maximum likelihood estimation method（MLE），maximum posterior estimation method（EAPE），expectation posterior estimation method（MAPE）and their variants，and discusses their advantages，disadvantages and applicable situations. In this paper，through CAT simulation design，different ability estimation methods are used in the CAT testing process and the final stage of CAT respectively，and the measurement attributes of the ability estimation methods in the CAT testing process are analyzed. It is found that under the methods of MLE，Biweight and EAPE-U（-4，4），CAT could achieve accurate measurement for all ability levels of the subjects. In the process of CAT test，when the ability estimation method of subjects is EAPE-N（0，1）or EAPE-N（0，2），and the final ability estimation method is EAPE-N（0，1）or EAPE-N（0，2），high-ability subjects will underestimate to a certain extent，the low-ability subjects overestimated to a certain extent，and the ability estimation was close to the middle. In addition，as long as EAPE-N（0，1）or EAPE-N（0，2）method is used in part of CAT stage，and other ability estimation methods such as MLE are used in other stages，the RMSE of intermediate ability subjects will be relatively small，while the RMSE of high-ability and low-ability subjects will be relatively large.

Key words：CAT，Maximum Likelihood Estimation，Expected A-Posteriori Estimation，Maximum-APosteriori Estimation

（责任编辑：吴茳）