变电站用铅蓄电池的温度估计与散热仿真

沈梦甜，康文，夏建勋，王春生，董垚林，周欣瑶，曹原*，陈有根

（1.国网湖南省电力有限公司超高压变电公司，湖南 长沙 410004；2.中南大学自动化学院，湖南 长沙 410083）

0 引言

变电站备用电源承担着向继电保护设备、自动投切装置等直流负荷供电的任务，在保障变电站直流系统稳定运行的过程中发挥重要作用[1]。目前变电站备用电源大多采用铅酸蓄电池。铅酸蓄电池具有技术成熟、容量大、成本低廉、免维护等优势[2]。

铅蓄电池在充放电过程中内部会累积一定热量，使电池温度高于外部环境温度。研究表明，铅蓄电池的温度在 25 ℃ 基础上升高 10 ℃，其寿命将缩短到原来的二分之一[3]。当系统负荷较大时，铅蓄电池的温度可能会超出适宜的运行范围，使电池老化加速、循环寿命缩短。这样将缩短电池的更换周期，使变电站的运维成本增加。热量的异常累计将会使铅蓄电池内部副反应加剧。当电池温度超出阈值，可能会引起热失控[4]。

变电站用铅蓄电池组的规模较大，而且各单体电池的更换周期不同，因此难以保证组内单体电池的参数一致[5]。对于个别内阻偏大的电池，若运行期间温度长期偏高，将会加剧电池劣化，形成恶性循环，最终可能引起热失控。此外，组内不同位置处的单体电池的散热条件存在差异，同样会引起电池组温度的不均衡。为了保障系统正常运行，电池组内最大温差需要尽量控制在 2 ℃ 以内。

目前，变电站用铅蓄电池通常不附加任何散热系统。在这种自然散热条件下运行的电池的温度将长期高于基准值，令电池无法达到理想寿命，在特定情况下可能会引发事故。若能实现对电池组内各单体电池的温度实时监测，并且附加强制风冷散热系统，将有利于保障电池发挥出理想性能，延长更换周期，避免安全事故。

为电池组附加合理的散热系统，首先需要对铅蓄电池组的热效应进行研究。如果仅采用实物实验的方式研究电池的热特性将会消耗大量的资源。采用计算机仿真技术，建立电池组的热效应模型，研究电池组在自然散热和强制对流下的温度分布，能够有效减少资源消耗，降低开发成本，并且便于进行优化设计[6]。

获取电池的内部温度是进行散热设计的基础。H.Dai 等人提出一种基于卡尔曼滤波和等效时变电网热模型的自适应温度估计方法，可以同时估计电池内部温度和外部热阻，并且由实验证明了方案的可行性[7]。C.G.Moral 等人利用开关电容均衡器的信号对电池内阻进行估计，再利用电池内阻估计电池温度[8]。H.Beelen 等人提出基于 EIS 的温度估计，用电池单个阻抗测量来估计温度[9]。M.M.Hasan 等人提出一种基于非线性自回归外生神经网络的数据驱动模型来估计公用事业规模中的电池单元温度[10]。

为了达到最佳的散热效果，需要根据电池组的特征设计合理的散热结构。李淼林等人以降低最高温度和组内温差为目标，基于正交试验对电池组的进风角度、出风角度和单体电池间距进行优化。与初始模型相比，优化后的模型电池组最高温度降低了 9.55 %，组内温差下降了 25.89 %[11]。宋俊杰等人设计了一种反向分层风冷结构，在附加扰流板的前提下，使电池平均温度下降 2.7 ℃，电池平均温差下降 0.6 ℃，而且散热性能显著提升[12]。K.Chen 等人对电池热管理系统（BTMS）中的一种弧形流道进行了结构优化，采用流阻网络模型来获取流体的速度场分布，而且利用计算流体力学（CFD）方法评估冷却效果，在将系统压降仅仅提高了 26 %的同时使电池组最大温差降低了 86 %[13]。在文献[14] 中 M.S.Wu 采用 CFD 方法对 U 型和 Z 型风冷结构进行比较，并且利用 Nelder-Mead 算法对电池组最高温度、组内温差和风扇功耗进行优化，证明在优化前后 U 型结构的冷却表现均优于 Z 型结构。F.Zhang 等人中通过增加二次出风口和挡板的方式对 Z 型风冷结构进行优化，研究了二次出风口与挡板的数量和宽度对 BTMS 冷却性能的影响。优化后的电池组最高温度降低了 4.2 %，组内温差降低了75 %[15]。以上文献均建立了电池组的热效应模型，并从不同的角度对散热结构进行优化，以达到最佳冷却效果。

本文中，笔者以电池的电热耦合模型为基础，提出了基于卡尔曼滤波算法的铅蓄电池内部温度估计方法，并以某型号阀控式铅蓄电池为研究对象，基于 ANSYS Fluent 软件建立小规模铅蓄电池组的三维模型，研究对电池施加强制风冷后的降温效果，为变电站站用铅蓄电池电源散热的优化设计和热管理提供思路。

1 铅蓄电池的温度估计与散热策略

铅蓄电池内部温度估计即估计电池的电芯温度。蓄电池的内部温度难以直接测量获得，但是由于电池的表面温度与内部温度并不一致，如果使用温度传感器测取电池表面温度的值当作内部温度，就会带来比较大的误差。目前常用的温度估计方法有基于电热耦合模型的温度估计、基于电化学阻抗谱（EIS）测量的温度估计、基于热模型与 EIS 测量相结合的温度估计、基于数据驱动的温度估计。本文中，笔者选择了基于电热耦合模型的温度估计方法。

1.1 电热耦合模型

在建立电池电热耦合模型时，可以分别独立建立电池等效电路模型与热模型，再将二者耦合。

在电池建模中，最常见的电模型是二阶等效电路模型。一方面，如果为了计算简单而选择理想电压源模型、纯电阻模型或者低阶等效电路模型，模型精度就会降低，不利于后续研究分析。另一方面，如果为了高精度的要求选择高阶等效模型，计算成本将大大增加，甚至难以求解。高阶电池的参数辨识过程困难、容易出错，而且精度提高有限，同样达不到理想的效果。综合考虑模型精度和计算难度，选择二阶 RC 等效电路模型较为合适。在图1 所示的二阶 RC 等效电路拓扑结构中，Cc表示电荷转移引起的电容，Rc表示电荷转移引起的电阻，Cd表示电荷扩散引起的电容，而Rd表示电荷扩散引起的电阻。

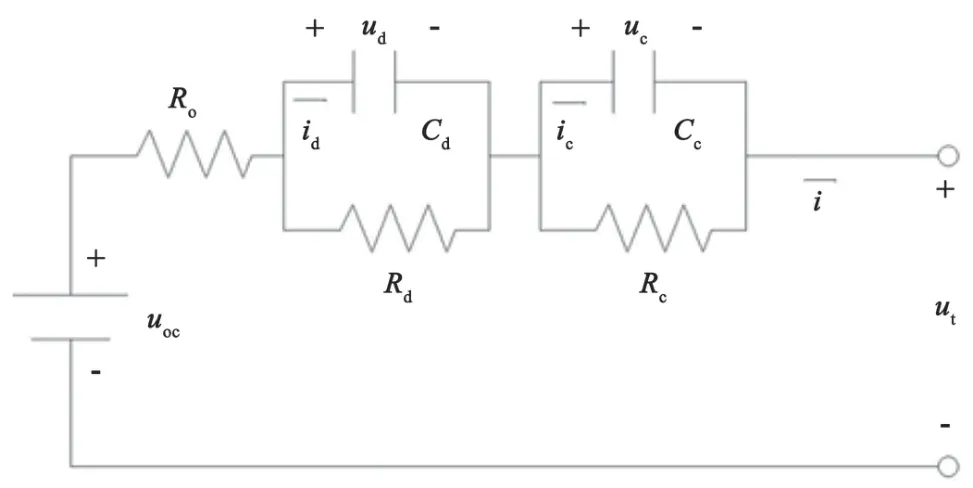
图1 二阶 RC 等效电路图

对铅蓄电池进行内部温度估计的必要前提就是构建电池热模型。根据 Bernardi 生热模型[16]，在搭建好电模型的基础上，可以搭建铅蓄电池的热模型。出于模型精度及搭建难度两方面的考虑，集总参数热模型是比较合适的选择。同物理系统可以有相似的动态特性方程，因而不同物理域内的变量也具有一定相似性。利用这个相似性，可以将电池的热特性等效为电特性。图2 中各参数具体如下：Q为内部热源（产热速率）；Ci、Cs分别内部热容及表面热容；Ri、Ro分别为内部热阻与外部热阻；Ts为电池表面温度；Ti为电池内部温度，即电池中心温度最高点；Tamb为环境温度。在锂电池集总参数热模型中，将热模型参数Ci、Cs、Ri及Ro以恒定不变的方式处理。整理得到如下

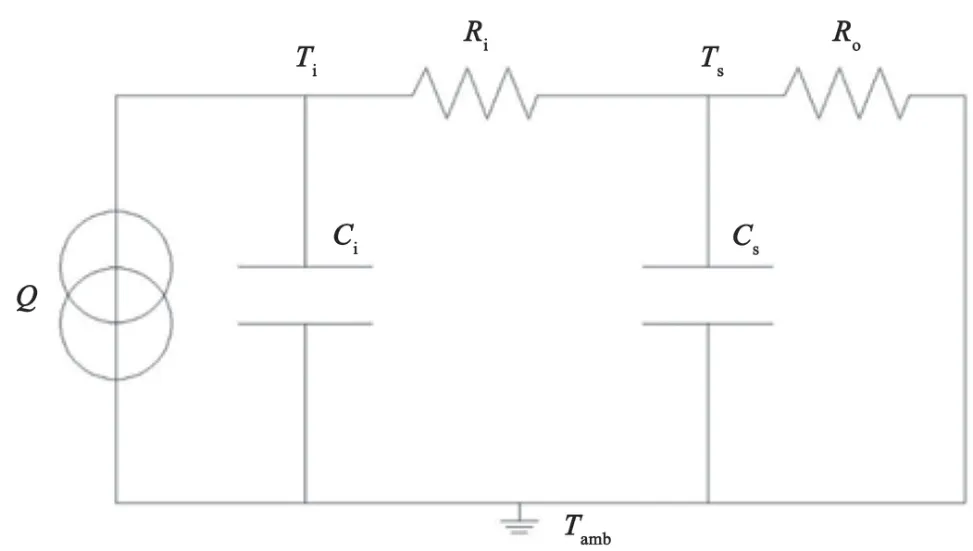
图2 热集总参数结构图

这样的关系式。公式（1）中，Tia、Tsa分别为内部温度和外部温度与环境温度的差。这是定义为内部温度的相对值与外部温度的相对值。

1.2 温度估计策略

卡尔曼滤波器通过在时间上递归地应用线性方程组，不断更新状态向量的估计值，并使用测量数据来纠正估计值，从而提高状态向量的精度。预测和更新是卡尔曼滤波算法的两大部分。在预测步骤中，通过系统的动态模型预测下一时刻的状态。在更新步骤中，将预测结果与测量值比较，通过卡尔曼增益修正预测结果，得到更准确的状态估计。

基于卡尔曼滤波算法的内部温度估计框架如图3 所示。电热耦合模型以电流作为输入，以温度作为输出，通过最小二乘法辩识得到热模型参数，然后以方便测量的表面温度作为观测值，且以表面温度和内部温度作为状态变量，通过卡尔曼滤波输出最终估计的内部温度。

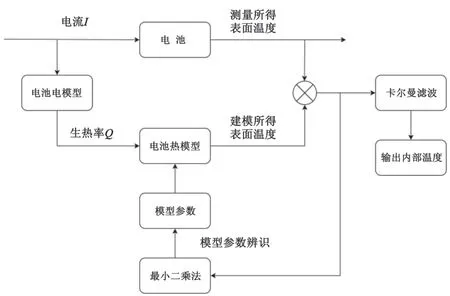
图3 温度估计框架图

将铅蓄电池集总热模型的表达式，即式（1），转换为状态空间方程

的形式。把内部温度的相对值Tia和外部温度的相对值Tsa作为系统的状态变量x，用电池的产热率Q作为输入u，以Tia作为输出y，利用上述关系式建立以下

状态空间方程。这个状态空间方程反映了系统内部和外部温度的相对值如何在电池产热率的影响下随时间变化。其中Tsa反映了系统内部的温度状态，所以在这里作为状态变量。与此同时，Tsa也是便于测量的结果，所以这里将Tsa作为输出变量，利于更好地了解系统的性能以及对外部环境的响应。

1.3 温度控制策略

自然散热条件虽然能够在大多数条件下满足铅蓄电池正常运行的需要，但是只能通过室内空调系统调节环境温度，无法实现对电池温度的控制。如果蓄电池的温度长期偏高，就无法达到理想的使用寿命，同时也会存在一定的温度不均衡现象。为了实现对站用铅蓄电池组更加有效的热管理，笔者将为电池组内任一单体电池附加散热风扇，并采用PID 控制风扇转速。

PID 即比例、积分、微分控制，在工程中应用极为广泛。若被控对象的结构和参数未知，无法得到精确模型，此时可以现场调试 PID 控制器的参数，得到理想的响应曲线。PID 控制的输入和输出关系满足公式

在公式（4）中，e(t)表示偏差值，即输入量和输出量之差，而Kp、Ki、Kd分别为比例增益、积分系数和微分系数。在实际应用中，往往通过多次采样来确定偏差量。离散后的 PID 控制公式为

图4 为散热风扇的控制框图。设定控制目标温度θset的值为 25 ℃，并通过上述第 1.2 节中的温度估计策略得到电池内部的平均温度θ。将目标温度θset与电池温度θ的差值输入 PID 控制器中，对电池温度进行控制。设定风速v与电池温度θ的关系满足公式

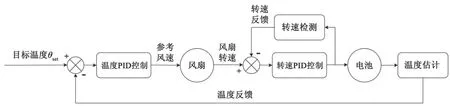
图4 散热风扇的控制框图

公式（6）中，v的单位为 m/s，θ的单位为 ℃。

2 铅蓄电池组散热模型

2.1 仿真对象

本文中，研究对象为某型号的阀控式铅酸蓄电池。单体电池的额定电压为 2 V，标称容量为 200 Ah。实验用软包电池的部分参数如下：质量 1 240 g；标称容量 200 Ah；额定电压 2 V；充电截止电压 2.4 V；放电截止电压 1.75 V；内阻 0.88 mΩ；5 s 最大放电电流 1 360 A；外形尺寸 90 mm×180 mm×350 mm。

2.2 三维模型

由于铅蓄电池电池内部结构复杂，而且副反应众多，因此难以建立精确描述电池各种行为的热模型。对本设计中的散热模型来说，可以忽略对实验结果影响不大的因素，得到电池的简化模型。具体考虑可忽略的影响因素如下：

（1）ADIVISOR 模型中将电池核心和电池外壳作为两个独立的等温节点。电池壳体内的所有部件，如活性材料、阴极和阳极、集电器、隔膜等，都假定为具有平均性质的单一均质材料。本设计中将同样把电池内部视为各向同性、均匀生热的单一材料，并且通过计算得出各参数。

（2）设定电池内部材料的密度、比热容和导热系数不随电池荷电状态（简称 SoC）和温度等因素变化而变化。

（3）不考虑电池内阻随 SoC 和温度的变化。

（4）忽略辐射换热。

220 V 变电站直流备用电源通常由 104 只额定电压为 2 V 的单体铅蓄电池串联组成。由于阀控式铅蓄电池的体积较大，且通常分布式排列在蓄电池室内，因此选取相邻的数只电池进行研究，即可得到有代表性的结果。本文中，针对 8 个单体电池串联构成的小规模铅蓄电池组展开研究。由于电池组模型的计算量极大，对计算机性能要求较高，因此需要对模型进行适当的简化。把电池组模型中的风扇扇叶、连接线、传感器等装置略去，将电池视为均一材料的生热源，并将散热风扇视为气流的速度入口。

图5 为电池组排列方式的示意图。图6 为电池组的三维模型图。模型中每只单体电池的上方均由一个风扇（直径为 12 cm）单独提供散热。三维模型图中的外部边界并非实体，允许气流自由流通。

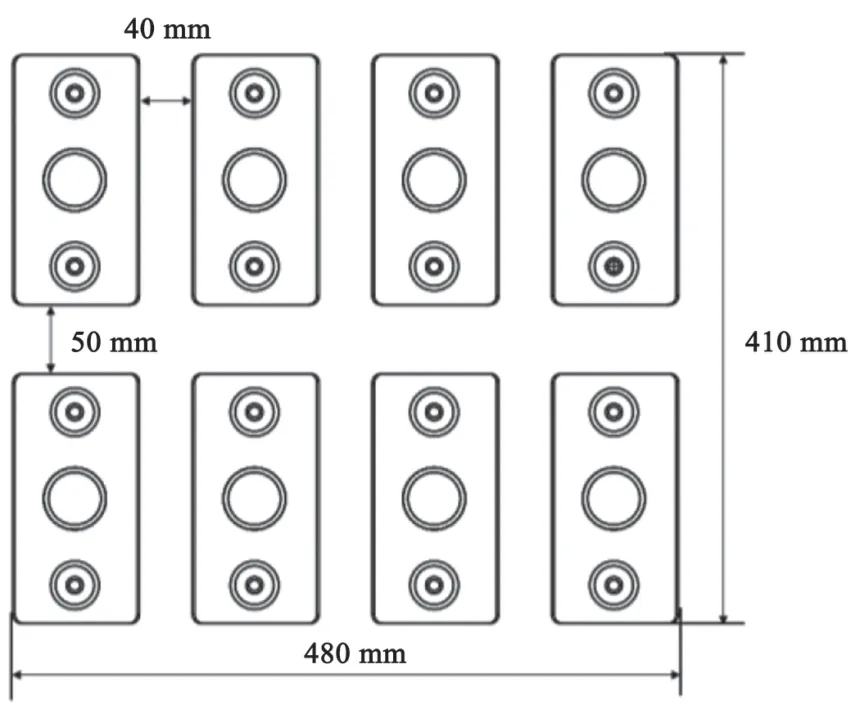
图5 电池组排列方式示意图

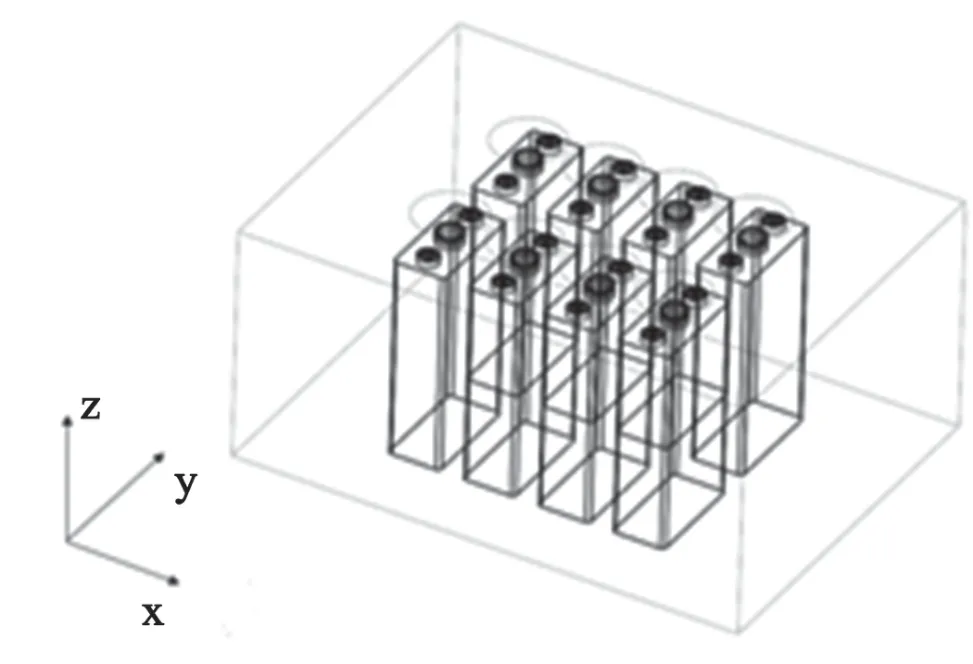
图6 电池组三维模型图

根据备用电源的实际工况，设定电池组的放电电流为恒定 45 A，环境温度为 25 ℃。对电池组无散热和附加散热后的温度场分布进行研究。

2.3 电池的生热与传热

铅蓄电池在充放电过程中进行着复杂的化学反应。这些反应均会吸收或放出热量。另外，电池运行中具有极化内阻Rp和欧姆内阻RΩ，在大电流充放电时也会释放可观的热量。锂离子电池在充放电过程中的热量来源通常可分为 4 类，分别是反应热Qr、极化热Qp、欧姆热Qj和副反应热Qs[11]。

实现实时监测电池的生热速率难度较大，在CFD 仿真中通常用 Bernardi 电池生热模型来计算电池生热速率：

公式（7）中各参数具体如下：V是电池体积，单位为 m3；E是电池的开路电压；U是电池的实际电压，单位为 V；dE/dT表征了温度对电池开路电压的影响，在工程应用中一般取常数；R为电池内阻，单位为 Ω。

铅蓄电池与外部环境的热量传递主要通过 3 种方式进行，分别是热传导、热对流和热辐射。在动力电池的风冷散热系统中，热对流是最主要的散热形式。热对流换热量的计算通常用牛顿冷却公式：

公式（8）中：Qc表示热对流下单位面积的传热速率，单位为 W；h表示对流传热系数，单位为 W/(m2·K)；A表示与传热方向垂直的接触面积，单位为 m2；Tw和Tf表示高温区域和低温区域的流体温度，单位为 K。

2.4 电池的热物性参数计算

Fluent 中仿真所需的电池热物性参数主要是材料密度、比热容和导热系数。电池内部由多种材料构成，所以其平均密度为组分的加权平均值，可由公式

计算得出。式（9）中，mi为电池内部材料 i 的质量，V为电池体积。忽略比热容随温度压力的变化，电池内部的平均比热容同样可由加权平均方法得到。计算式为

铅蓄电池内部由正、负极板和隔板逐层堆叠构成的极群浸润在电解液中，所以铅蓄电池的导热系数具有各向异性，在仿真中可视为沿 x、y、z 方向导热系数不同。考虑到电池内部极群的堆叠方式，x 方向的导热系数应该远小于 y、z 方向的。各项导热系数的计算公式如下：

其中：λx、λy、λz分别是各向导热系数；λp、λs、λn分别是正极、隔膜和负极材料的导热系数；δp、δs、δn分别是正极、隔膜和负极材料的厚度；b、l、h分别对应电池在 x、y、z 三个方向的尺寸。

3 实验结果与讨论

由于铅蓄电池运行的基准温度为 25 ℃，因此若长时间在 35 ℃ 左右的高温下运行，电池寿命将会大幅衰减，使变电站的运维成本将大大增加。如果散热不良导致温度升高到 60 ℃ 以上，电池的塑料外壳可能无法承受，出现变形、鼓包的情况，甚至有外壳破裂、电解液泄露的危险。此外，由于工艺、循环周期、温度等原因，铅蓄电池组内的单体电池内阻存在差异。根据电池生热速率模型可知，内阻大的电池的温度会比其他电池的温度高，导致组内的电池温度不均衡。对于铅蓄电池来说，温度偏高会加剧水分解等副反应进行，使内部电解液减少，以及内阻进一步增大，更严重时可能会引发热失控。因此，有必要对变电站用铅蓄电池组进行温度场仿真。

考虑到电池内阻不均衡的情况，引入散热风扇，将运行温度控制在合理范围内。首先，对无散热情况下铅蓄电池组正常运行时的稳态温度场进行研究。然后，在此基础上研究附加散热风扇后的降温作用，并验证采用上述温度控制策略对内阻不均衡电池组的冷却效果。

3.1 无风扇散热情况下电池组温度场分布

电池组即使不存在内阻不均衡的情况，在正常运行期间也会存在温度不一致的现象。并且，随着放电倍率的提高，电池组内的温度会更加不均匀。备用电源正常运行期间，电池组内的最高温度和最低温度之差最好控制在 2 ℃ 以内。

设定初始温度为 25 ℃，得到无散热情况下铅蓄电池组正常运行期间的稳态温度场如图7 所示。图7 中电池组的最高温度在 34.5 ℃左右，最低温度约为 33 ℃，即最大温差在 1.5 ℃ 左右。位于中心的电池热交换条件较差，所以其温度显著高于两侧的电池。在这样的温度下长期运行，将加速铅蓄电池的劣化过程，使电池提前报废，造成不必要的资源浪费。

图7 铅蓄电池组温度分布

如果考虑电池组内阻不均衡的情况，得到无散热情况下电池组的温度分布如图8 所示。两种情况下电池组的温度如表1 所示。此时电池组最高温度上升到 37 ℃，最大温差增加了 1 倍，达到了 3.2 ℃。电池组内温度不均匀程度显著增加。当组内部分电池的温度远高于其他电池时，高温会加剧电池内部水分的蒸发和电解，导致内阻增大，形成恶性循环，最终可能使局部温度失去控制。

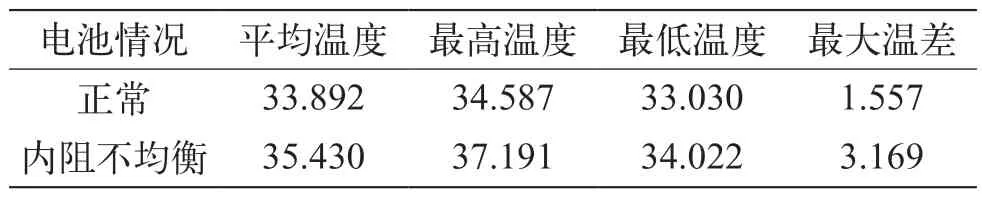
表1 无散热情况下电池组的温度 ℃

图8 内阻不均衡的铅蓄电池组温度分布

综合以上仿真结果，变电站铅蓄电池系统需要附加合理的主动散热措施，控制电池的运行温度。

3.2 附加散热风扇后电池组温度场分布

在第 3.1 节中电池组基础上附加散热风扇，使风扇产生气流的平均风速分别为 0.2、0.5、0.8、2.0 m/s，得到的电池组的温度如表2 所示。电池组稳态温度场分别如图9～图12 所示。由仿真结果可知，附加散热风扇能够大幅降低电池组的温度。即使风速仅有 0.2 m/s，降温幅度仍能达到 6.7 ℃，能够将电池正常负荷运行下的温度控制在 25 ℃ 左右。电池组温度随着风扇转速的提高而降低，但是当风速到达0.8 m/s 左右时，提高风速的效果不再明显。在风速为 0.2 m/s 时，电池组内的最大温差控制在 0.72 ℃，仅为无散热条件下的一半左右。随着风扇转速提高，电池组内最大温差进一步减小。由此可见，附加散热风扇显著改善了铅蓄电池组的温度均匀度。

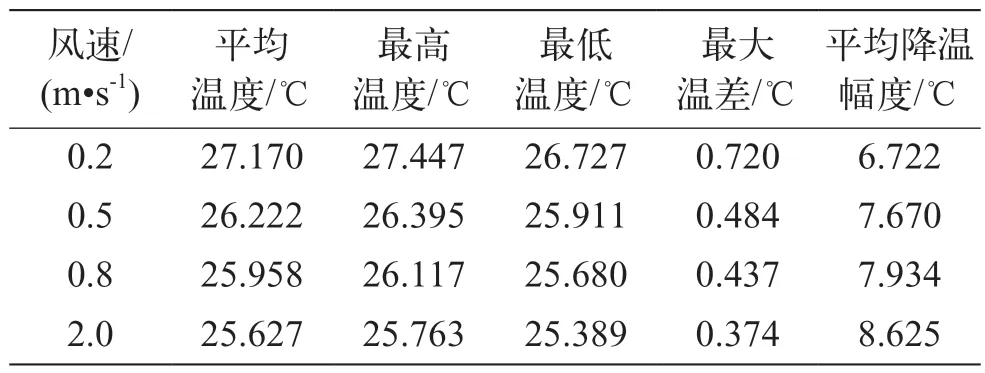
表2 附加散热风扇后电池组温度

图9 风速 0.2 m/s 时铅蓄电池组温度分布

图10 风速 0.5 m/s 时铅蓄电池组温度分布

图11 风速 0.8 m/s 时铅蓄电池组温度分布

图12 风速 2.0 m/s 时铅蓄电池组温度分布

在第 3.1 节中对内阻不均衡情况下电池组的稳态温度场进行了研究，现根据不同电池的温度调整对应散热风扇的转速，加强高温电池与空气的对流换热，得到附加散热后内阻不均衡电池组的温度分布如图13 所示。调整风扇转速后，电池组的平均温度为 26.25 ℃，最大温差为 0.96 ℃。与无散热时平均温度 35.43 ℃，最大温差 3.169 ℃ 相比，电池运行期间的温度状况显著改善，大大减缓了个别电池的老化过程，降低了局部热失控的风险。

图13 调整风扇转速后内阻不均衡电池组的温度分布

综合来看，附加合理的散热结构能够大幅降低变电站铅蓄电池组的运行温度，将电池组平均温度控制在基准温度 25 ℃ 左右，组内最大温差控制在1 ℃ 以内，能够延长电池寿命，减小维护和更换电池的成本，减小故障风险。

4 结论

本文中，笔者提出了一种基于卡尔曼滤波算法和电热耦合模型的电池温度估计方法，以及由 PID控制风扇转速的风冷散热系统。该风冷散热系统包括了电池单体温度估计和电池组散热。仿真结果表明，在初始温度同为 25 ℃ 的条件下，基于 PID 控制风扇转速来散热的电池组平均温度相较于未加散热的电池组下降了 9.18 ℃，且电池组内最大温差下降了 2.209 ℃。

与常见的未加散热系统仅凭自然散热的变电站用铅蓄电池相比，附加散热系统可以保障电池组在合适的温度下运行，并且减小组内电池温度差，提高电池组温度均匀度，对实现变电站用铅蓄电池的长久安全运行有重要意义和工程实践价值。