随机工况主动式动压型干气密封调控力智能预测及其算法性能对比研究

卓志愿, 陈 源*, 李运堂, 王冰清, 金 杰, 彭旭东

(1.中国计量大学 机电工程学院, 浙江 杭州 310018;2.浙江工业大学 机械工程学院, 浙江 杭州 310032)

干气密封(Dry gas seal，DGS)是一种广泛应用于中、高速旋转机械的非接触式轴端密封形式[1-2]，具有泄漏小和可靠性高等优点[3].目前工程应用的动压型DGS多属于“被动式”结构，即密封相关参数基于特定操作条件进行设计，无法随运行环境改变做出适应性调整.这使得动压型DGS在运行过程中常因转速或介质压力[4-5]变化导致膜厚失稳，进而出现密封环撞碎或端面磨损等情况.为此，胡松涛等[6]、Blasiak等[7]和王杰等[8]开展了型槽结构参数和弹簧刚度等力学参数的协同设计与相关特性研究，旨在改善DGS的运行稳定性.为进一步提升动压型DGS在变工况下的适应性和稳定性，本文中研究团队借鉴气压调控技术和智能材料驱动技术在静压型DGS[9]及气浮轴承[10-12]上的成功应用经验，提出了1种闭合力可控的主动式动压型DGS结构[13].

为实现变工况下动压型DGS闭合力的精准调控，准确掌握密封在不同工况下的开启性能及膜厚变化规律至关重要.江锦波等[14]通过有限差分法编程求解雷诺方程，研究了工况参数对动压型DGS性能的影响规律，结果表明性能受转速和介质压力影响显著.彭旭东等[15-16]同样利用有限差分法求解雷诺方程，分析了介质压力对密封端面开启性能的影响，并指出开启特性与膜厚稳定性是保障动压型DGS可靠运行的关键.张伟政等[17]和王衍等[18]则采用有限元仿真软件探究了工况对DGS性能的影响.值得注意的是，目前DGS相关性能多采用编程求解或利用有限元软件仿真计算，计算过程复杂且速度较慢.因此，有必要引入合适的智能预测算法，基于有限样本快速且精准完成变工况下维持膜厚稳定所需调控力的智能预测.

近年来，智能预测算法在机械等工程领域得到广泛应用.刘正先等[19]建立多元线性回归(Multiple linear regression，MLR)模型，以工况与膜厚为自变量，精准预测了DGS的开启力.Ma等[20]建立更精确的反向传播(Back propagation，BP)神经网络模型，用于预测液压膨胀装配凸轮轴的主要失效因素.此外，Guo等[21]采用径向基函数(Radial basis function，RBF)神经网络与遗传算法相结合的多目标优化方法预测了离心泵的效率，并实现了液压和声学性能的协同优化.Ghritlahre等[22]利用RBF神经网络和前馈神经网络等算法预测加热器的排气性能，发现RBF神经网络在平均绝对误差和均方根误差方面表现较好.章聪等[23]采用BP神经网络在转轴密封中实现了临界区CO2的物性预测，相较于REFPROP 软件提供的优选物性预测模型，BP神经网络可明显降低近临界点区的物性预测平均误差.Du等[24]比较研究了MLR、BP神经网络和RBF神经网络等算法在真空管太阳能集热器热规律上的预测性能.上述研究表明，合理运用符合主动式动压型DGS需求的智能预测算法对于提高参数预测精度和性能调控效率至关重要.

本文中以主动式螺旋槽DGS为具体研究对象，以介质压力和转速作为输入特征，调控力作为目标变量，基于拉丁超立方抽样方式采集调控力样本数据.对比研究MLR、局部加权线性回归(Locally weighted linear regression，LWLR)、BP和RBF神经网络等4种常用智能预测算法的性能，以期为变工况下主动式动压型DGS性能调控提供一定的理论参考.

1 理论模型

1.1 主动式动压型DGS结构与原理

图1所示为主动式动压型DGS结构示意图，其中磁控形状记忆合金和气控弹簧组成的控制单元，通过调节弹簧压缩量和刚度来调控闭合力.在设计工况条件下，密封端面形成1层稳定厚度的气膜，但在工况变化时，膜厚亦将随之变化并影响密封性能，本研究对象理论上可通过控制单元对静环背部施加调控力以适应工况变化，从而有效维持膜厚稳定.

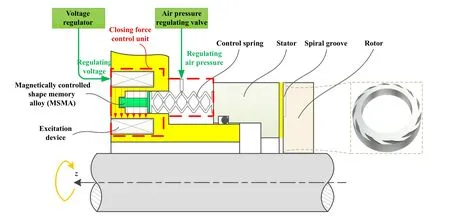
Fig.1 Schematic diagram of an active hydrodynamic pressure DGS图1 主动式动压型DGS结构示意图

1.2 数学模型

1.2.1 气体润滑理论模型

假设密封端面间为层流、等温[25-27]的理想气体，忽略温度和压力对气体黏度的影响，同时忽略离心力和惯性力的作用，则在极坐标下可压缩气体的稳态雷诺方程[28]为

引入无量纲变量：

式中，p为端面气膜压力；pa为环境大气压力；h为端面稳态气膜厚度；h0为台区膜厚；Λ为压缩数；μ为气体黏度；ω为角速度；ri为密封端面内半径；r和θ为极坐标系中的半径和角度.

则无量纲稳态雷诺方程的表达式如下：

强制性边界条件：

周期性边界条件：

式中，ro为密封端面外半径；po为密封介质压力；pi为大气压力；Ng为周期数.

当动环旋转时，气体泵入密封端面，在流体动静压效应作用下的气膜压力使端面开启.图2所示为密封挠性安装静环的受力示意图，开启力[29]表达式如下：

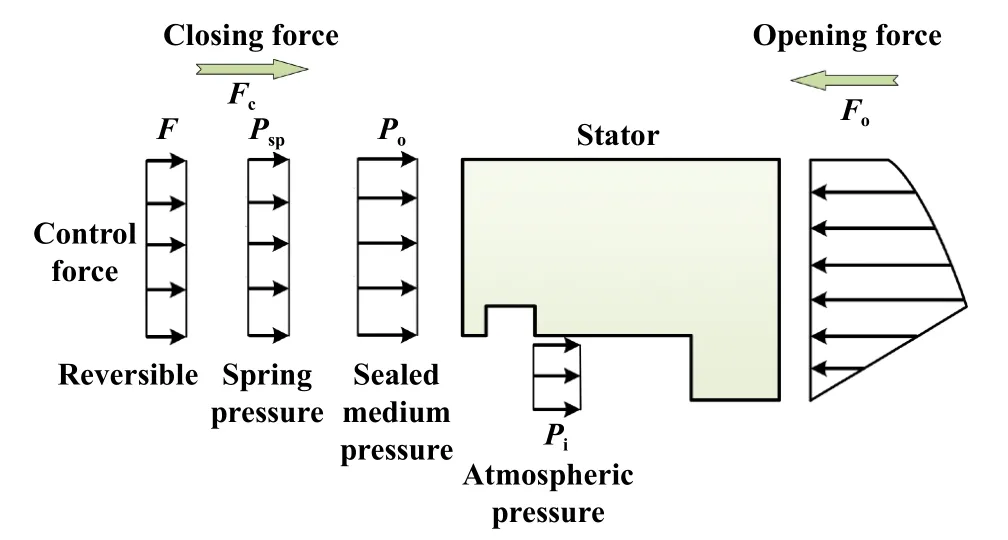
Fig.2 Schematic diagram of end face force图2 端面受力示意图

在稳态条件下，密封环端面的闭合力有助于保持密封面之间的合适距离和气膜稳定，密封运行稳定后与开启力大小相等，方向相反，闭合力主要受弹簧比压和内外径介质压力的影响.当工况变化时，平衡膜厚将偏离设计值，需提供调控力来维持膜厚稳定，工况变化后，调控力的大小可以通过闭合力与膜厚在预期设计值下的开启力之差来确定.通过数值分析计算完成随机工况下调控力的样本采集，以用于后续算法模型训练.闭合力Fc和调控力F的计算表达式分别如式(7)和式(8)所示[30]：

式中，psp为弹簧比压；rb为平衡半径.

1.2.2 4种典型智能预测算法模型

(1)多元线性回归

通过MLR完成多个输入特征的线性预测，引入损失函数评估模型并采用梯度下降法进行回归系数θ的局部最优求解，MLR模型方程式和损失函数表达式如式(9)和式(10)所示，本文中研究最终确定三个回归系数分别为-186.2、253.6和111.2，学习率为0.1.

式中，Xj为特征自变量；J(θ)为损失值；m为样本数；F(X(i))与y(i)分别为第i个样本的预测值和实际值.

(2)局部加权线性回归

局部加权线性回归(Locally weighted linear regression，LWLR)属于非参数化算法，在MLR方程中引入加权参数，预测任一点需对所有样本点赋不同权重W进行局部拟合，并基于最小二乘估计求得当前预测点的局部θ.本文中权函数W选取高斯核函数，加权宽度τ取1.2，W表达式如下：

式中，XΔ为当前预测样本.

(3) BP神经网络

BP神经网络具有良好的非线性预测能力，模型设计图如图3所示.包括输入层、隐含层和输出层，为达到模型的最优性能，本文中通过交叉验证的方式确定最终隐藏层神经元个数为8，选择Rule激活函数和Adam优化器，设置L2正则化防止过拟合，添加第2层隐藏层进一步优化预测效果，并确定其神经元个数为6.

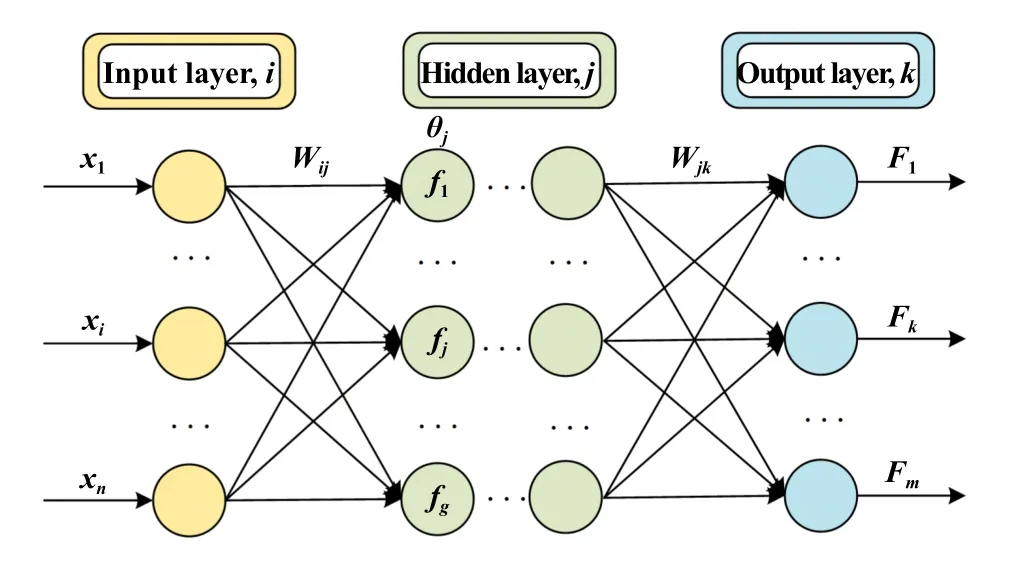
Fig.3 BP Neural Network Model Design图3 BP神经网络模型设计

隐含层各神经元的激活值为

式中，wij为连接权；θj为阈值.

将激活值代入激活函数f(S)可求得各节点的输出值，f(S)选取如下：

若预测精度不够则转入反向传播过程，将输出误差逐层反转，调节各层的连接权和阈值来提升精度.

(4) RBF神经网络

RBF神经网络是1种3层神经网络，模型设计如图4所示，与BP神经网络相比仅有1层隐含层，通过非线性映射将低维线性不可分的情况映射到高维空间，使其线性可分，输出是隐单元的线性加权和，本文中确定隐藏层神经元个数为12，使用Kmeans聚类算法设置神经元的初始化中心，选择RMSprop优化器，带宽σ设置为0.2.

Fig.4 RBF Neural Network Model Design图4 RBF神经网络模型设计

激活函数选取如下：

式中，xp为第p个输入样本；ci为第i个中心点.

1.2.3 预测模型评估指标

为评估MLR、LWLR、BP神经网络和RBF神经网络等算法对调控力的预测效果，采用最大正向偏差(ΔFp)、最大负向偏差(ΔFn)、平均绝对误差(MAE)、平均相对误差(MARE)以及均方根误差(RMSE)作为评估指标，测试集采用直接误差ΔF和相对误差δ进行评估.指标表达式如下：

式中，Fobt为样本值；Fpre为预测值；N为样本数.

2 结果讨论与分析

主动式螺旋槽DGS性能计算在未加特别说明的情况下，所采用的工况及结构参数均列于表1中.本文中研究的设计平衡膜厚h0为3 μm，重点开展转速为9 000~11 000 r/min，介质压力为0.25~0.35 MPa的工况变化范围内的性能分析及调控力预测.

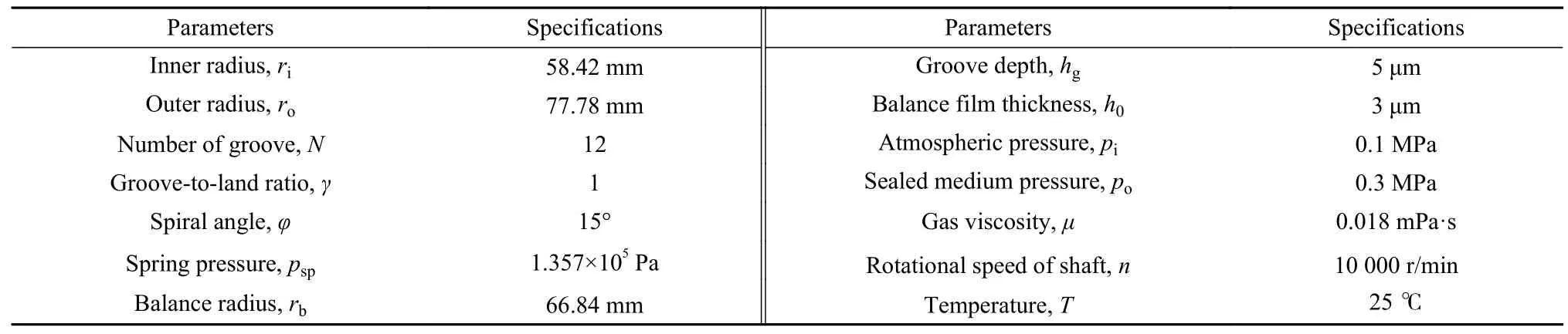
表1 初始参数数值表Table 1 Initial parameters

2.1 变工况密封性能参数仿真分析

图5所示为不同工况参数下的膜压p0分布云图，对比图5(a)、(b)和(c)可知，转速对膜压分布有显著影响，随着转速由9 000 r/min增大至11 000 r/min，螺旋槽端面泵入的气体介质在槽根处的挤压作用加强，不仅形成局部高压，整体膜压也明显升高.对比图5(b)、(d)和(e)可以看出，随着介质压力由0.25 MPa增大至0.35 MPa，端面膜压变化显著，受外径边界条件变化的影响，径向压力梯度更大，膜压分布亦受到较大影响.上述结果表明工况变化可通过影响膜压分布规律和数值大小，使开启力发生显著变化进而导致膜厚变化.

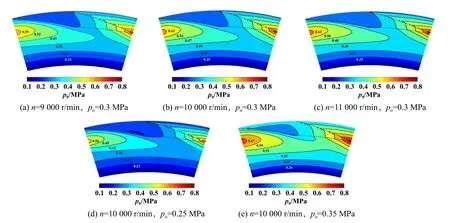
Fig.5 Sealing end face film pressure maps under different rotational speed and sealed pressure图5 不同转速和介质压力条件下密封端面膜压云图

为进一步研究工况随机扰变所带来的影响，本文中在工况研究范围内随机选定50组工况组合，分析了变工况下膜厚和开启力的分布情况.如图6(a)所示，随着转速和介质压力的增加，膜厚整体呈递增趋势.这是因为工况参数增大会提升开启力，为保持力的平衡，膜厚相应增大.由图6(b)可知，开启力受介质压力影响显著，但基本不受转速影响.这是因为DGS运行时处于等闭合力条件下，转速变化时闭合力基本不变，开启力将通过膜厚动态调整最终与闭合力平衡.从定量上分析，开启力在400 N的范围内波动，使开启力相比原工况下发生最大7.99%的变化，直接造成膜厚发生-7.49%到7.32%的变化影响，工况变化引起的膜厚过小或过大对密封都会带来不利影响.由图6可知，很难直接通过简单的拟合进行准确预测，需进一步引入智能预测算法.

Fig.6 Sealing parameter distribution diagrams under disturbance conditions图6 不同工况变化下的密封参数分布图

2.2 调控力预测性能分析

2.2.1 样本数据采集与处理

通过拉丁超立方抽样—1种均匀分布的空间采样方法，构建了816组不同工况特征的空间分布，基于表1所列工作条件与运行参数，通过数值计算获取试验样本，划分其中800组样本用于训练算法模型，剩余16组样本作为测试集，用于评估预测精度.部分测试点列于表2中，可知不同工况所需的调控力差异显著，此外，由计算时间t0可知，通过数值求解获取调控力理论值耗时较长.

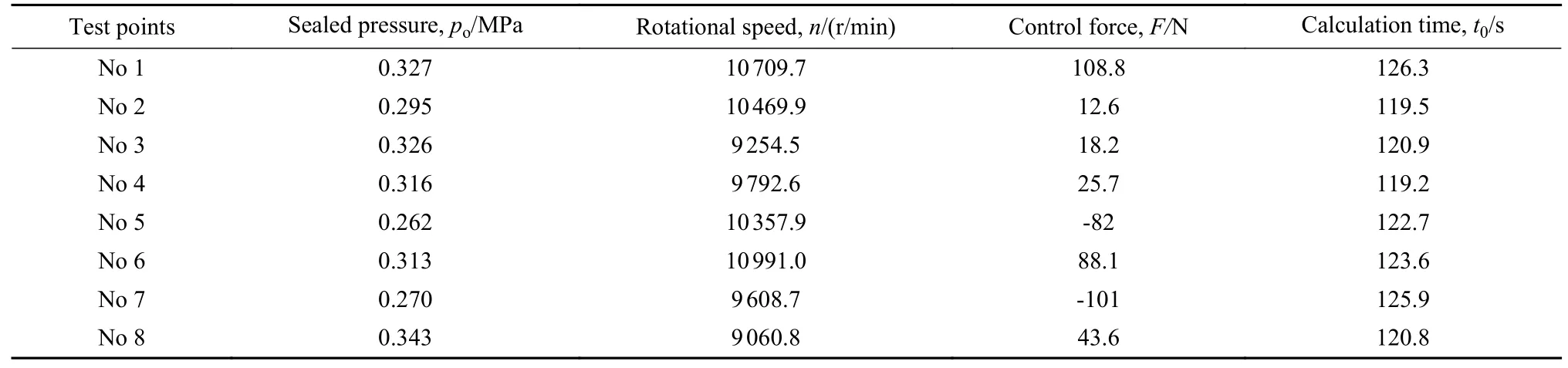
表2 测试集部分测试点Table 2 Partial test points in the test set

由于转速和介质压力两者的数据量级差异较大，可能导致无法收敛，因此需要将训练集和测试集做归一化处理，公式如下：

式中，Xnorm为标准化值；X为样本数据；Xmax为样本中最大数据；Xmin为样本中最小数据.

2.2.2 算法模型的训练过程及结果

训练样本的数量对算法模型的训练程度和预测精度至关重要.在不同样本数下完成模型的训练并针对训练集的调控力进行预测，如图7所示，以BP神经网络为例，低样本数训练的模型预测能力不足，其预测值与数值计算理论值有较大差异；高样本数下预测结果与理论值拟合程度较好.可见，训练集数量对模型的训练程度有着重要影响.

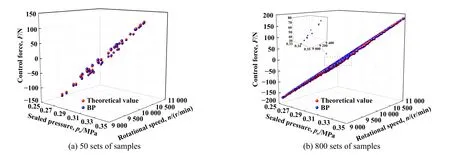
Fig.7 Scatter plot of theoretical and predicted control force by BP under different training sample sizes图7 不同训练样本数下BP神经网络的调控力理论与预测结果散点图

图8所示为4种典型算法在训练样本数m对MARE、RMSE和MAE3种调控力预测性能评估参数的影响曲线.由图8(a)可知，4种模型的调控力预测MARE随着m的增加而减小，低训练样本数下，由于RBF神经网络的输入矢量映射到隐空间的不确定性，导致模型的学习程度低且预测结果欠拟合.BP神经网络和RBF神经网络在m达到700后基本保持稳定，其MARE分别为0.88%和2.95%，对于MLR和LWLR而言，在m为500时足以完成模型的最优训练.此外，由图8(b)和(c)可知，相较于其余3种模型，BP神经网络预测的RMSE和MAE同样表现最优，分别为0.22和0.14，对于MLR和LWLR，m对RMSE和MAE的影响不大.鉴于样本的变化有一定规律且分布相对均匀，过拟合的风险较低，考虑更低的模型训练成本，故选取700组样本用于构建BP和RBF神经网络的模型，500组样本用于构建MLR和LWLR模型.

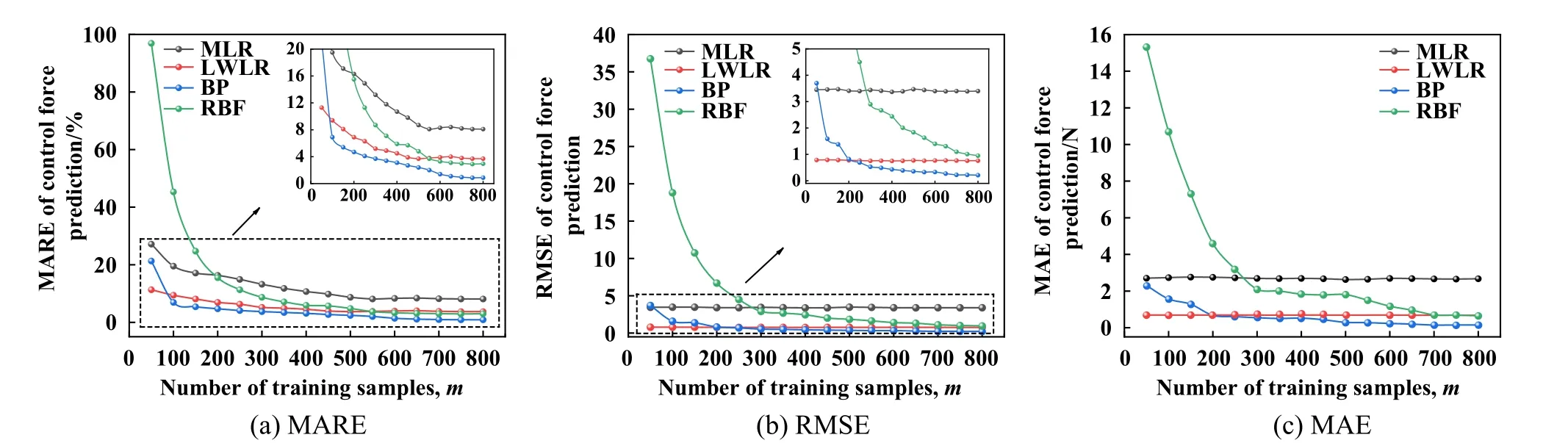
Fig.8 Influence of different training sample sizes on performance evaluation parameters of control force prediction curve图8 不同训练样本数对调控力预测性能评估参数的影响曲线

2.2.3 测试集预测误差检验

完成对最优训练样本数和模型参数的选择后，需通过测试集来验证模型对非训练数据的预测能力，仅对模型输入特征变量，将预测结果与基于表1运行参数下的数值分析计算结果进行比较，进而体现预测的准确性以及可信度.图9所示为4种算法在测试集工况下的预测结果与数值计算结果的对比.从图9中可知，BP神经网络的预测值与理论值最为接近，而MLR的预测值和理论值存在较大差距.此外，图10所示为算法在测试集工况下的预测误差散点图，可以观察到，BP神经网络预测的直接误差ΔF均控制在1 N以内，相对误差δ最小且多个测试点低于1%，而MLR预测的ΔF在-6~12 N之间大幅度波动，因样本呈非线性分布导致误差最大，多个测试点的δ高于10%，LWLR和RBF神经网络预测的ΔF处于-2~2 N之间，δ大小接近.通过测试集的误差检验进一步验证了BP神经网络在主动式动压型DGS调控力预测方面的优越性.

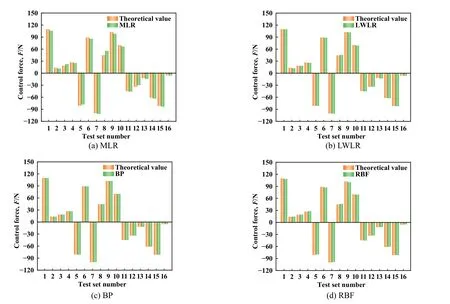
Fig.9 Comparative graph of predicted results and numerical calculation results of different algorithms under test set conditions图9 不同算法在测试集工况下的预测结果与数值计算结果的对比图

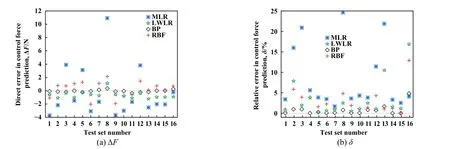
Fig.10 Scatter plot of prediction errors of different algorithms under test set conditions图10 不同算法在测试集工况下的预测误差散点图

2.2.4 训练集与测试集整体评估

图11所示分别为4种算法模型的整体评估精度特征雷达图.由图11可知，训练集与测试集在各项评估指标上的分布规律类似，训练集除ΔFp和ΔFn外，其余指标均略优于测试集，并且未出现过拟合的情况.综合各评估指标，BP神经网络展现了最优的预测精度，其次是RBF神经网络和LWLR.此外，由预测平均时间t可知，MLR和RBF神经网络的预测速度最快，而LWLR在预测时需遍历全部样本导致t最长.综合2.2各节结论，若膜厚调控对时效性要求极高，则优先考虑选取RBF神经网络；若综合考虑计算速度和预测精度，BP神经网络性能最佳.因此从综合性能来看，BP神经网络更适用于主动式动压型DGS在工况变化后的调控力预测.

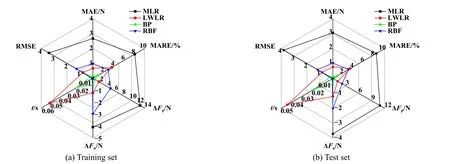
Fig.11 Radar chart of prediction accuracy characteristics图11 预测结果精度特征雷达图

2.3 变工况下调控力对密封性能的影响

通过BP神经网络完成测试集的调控力预测，结果输入至静环背面并基于等闭合力条件进行膜厚调控，若数值分析计算结果的调控膜厚误差足够小，则说明BP神经网络预测的调控力足以使膜厚恢复并有效提升密封运行的稳定性.

图12所示为施加预测调控力前后16组测试点的密封性能变化情况.由图12(a)可知，16组工况测试点的膜厚因工况变化呈现出不同的结果，当膜厚小于平衡膜厚设计值时，需通过控制单元施加反向调控力，使膜厚尽可能恢复至设计值；同理，当膜厚大于设计值时，需施加正向调控力.结合图12(b)可知，利用BP神经网络完成所有测试点的调控力预测，并施加于静环背面后，各工况测试点的平衡膜厚与设计值极为接近.经计算，16组测试点调控后的平衡膜厚与设计值的平均相对误差约为0.2%，达到维持膜厚稳定的预期.

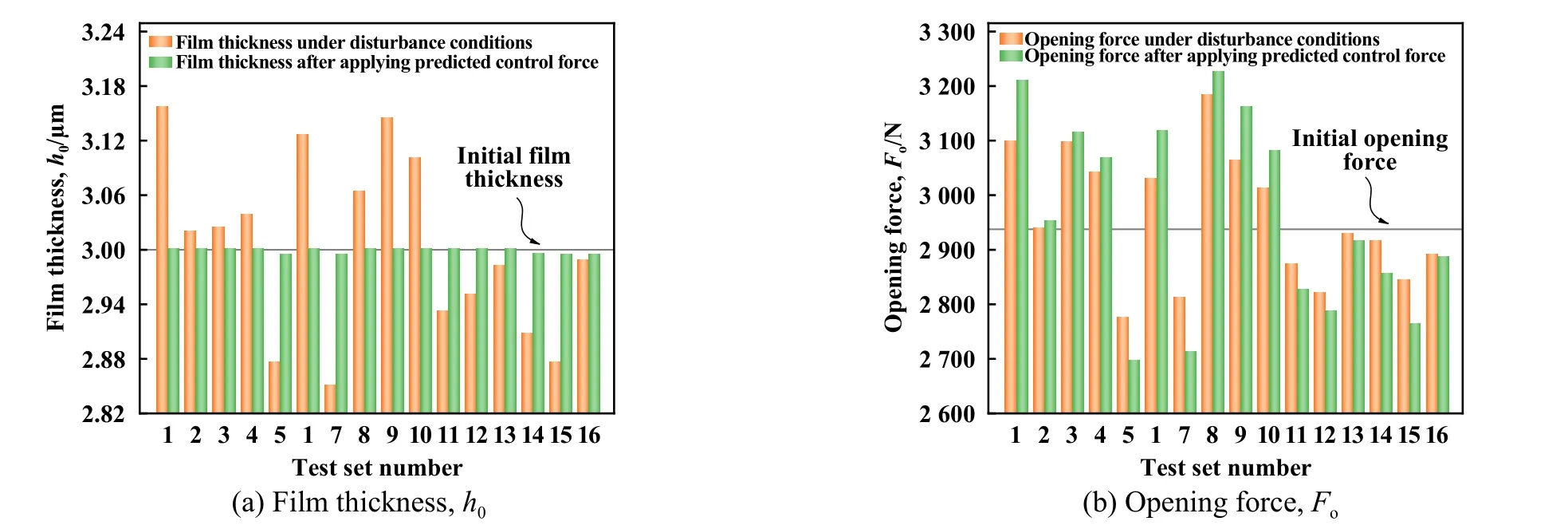
Fig.12 Bar chart of sealing performance (h0, Fo) comparison before and after applying control force图12 施加调控力前后的密封性能(h0, Fo)对比柱状图

3 结论

a.密封运行过程中的工况变化直接影响端面膜压，导致开启力和膜厚波动，易造成密封失稳或性能劣化，通过及时调控闭合力可有效提高密封性能.

b.随着训练样本数的增加，算法模型的泛化能力与预测性能均得到有效提升，综合考虑计算效率和预测精度，MLR、LWLR、BP和RBF神经网络的最优训练样本数分别为500、500、700和700.优化后的BP神经网络具有较高的预测精度和较快的计算速度，优先推荐该模型用于主动式动压型DGS在变工况下的膜厚调控.

c.工况变化后，将BP神经网络预测的调控力施加于静环背面，平衡膜厚受调控力驱动可有效恢复至近平衡膜厚设计值且平均相对误差仅0.2%，表明优化后的BP神经网络对变工况下调控力的预测结果符合膜厚调控的精度要求.