表面形貌对浮动式箔片气膜密封性能的影响分析
徐 洁, 俞树荣, 杨小成, 丁雪兴, 蒋海涛
(兰州理工大学 石油化工学院, 甘肃 兰州 730050)
浮动式箔片密封是针对火箭涡轮泵、航空发动机主轴承的密封需求提出的1种新型非接触式密封结构[1-2],即在柱面气膜密封的基础上,设计具有自适应变形能力的弹性箔片代替刚性密封面,以此来提高系统的抗干扰能力.在进行此类研究时,大多数公开的成果是将密封摩擦副视为光滑表面[3-4],但在实际中,完全光滑的表面是不存在.任何摩擦界面都是由许多不同的微凸体和微凹坑组成的[5-6],同时,为提高动压效应和改善摩擦性能,通常会在摩擦副表面设计螺旋槽和T型槽等造型[7-8],再次加工后的工作表面会呈现出不同的表面几何特征,而槽型和粗糙度的准确控制依旧是高精密加工工艺的探索课题[9].
粗糙度对气膜密封影响的研究主要集中在端面干气密封结构上.李伟等[10]利用有限单元法分析了粗糙度对螺旋槽干气密封的影响,表明粗糙度与膜厚的大小有关,且在低速运转时对密封性能的影响较大.刘梦静等[11]采用Greenwood和Tripp提出的三维随机粗糙模型[12],求解了同时考虑滑移流效应和表面粗糙度的流体润滑模型,发现较大的粗糙度均方根或者较小的粗糙峰间距都容易导致负滑移现象发生.毛文元等[13]将非槽区的密封端面假设为光滑表面,认为槽底的实际粗糙度呈正弦曲线分布,指出当粗糙度大于0.8 μm时,槽底的表面粗糙度对开启力和泄漏率的影响是不可忽略的.王学良等[14]针对柔性箔柱面气膜密封结构,通过数值模拟和试验测试的手段,发现箔片和轴套的表面粗糙度越大,越有利于提高气膜浮升力,但这对泄漏率和稳定性的控制不利,因而建议在工程应用中提高表面性能,同时,他们也针对该结构进行了静态和动态特性的理论预测[15].在进行柱面气膜密封的研究时,俞树荣等[16]采用商业软件对窄端面浮环的柱面气膜密封进行了数值模拟,并设计无槽和螺旋槽的轴套进行对比试验,结果表明,动压槽对提高浮升力发挥积极作用,对泄漏量的减小发挥负面作用.Lu[4]经过试验验证建立了高精度润滑计算模型,并基于开漏比的多目标优化函数对柱面密封的动压槽进行设计.马纲等[17-19]通过计算发现,柱面气膜密封的直接动态系数变化呈现一致性,而交叉动态系数变化呈现对称性.
在真实表面的数值模拟方面,邓可月等[20]采用Weierstrass-Mandelbrot分形函数模型,分别仿真模拟了二维和三维的轮廓曲线,并分析了不同分形参数与表面轮廓形貌复杂程度的关系.武胜超和祝胜光[21-22]针对真实表面特性的测量方法和特征提取等也有所研究,并将仿真表面与原始表面进行对比分析,得到更加接近原始表面的分形参数取值.此外,关于粗糙表面在其他领域的影响分析也得到了较多关注,例如,Kazuhiko[23]等通过柱塞副油膜振荡试验发现柱塞副油膜的运动状态与表面粗糙度密切相关,朱一萍[24]在研究压力容器中的气体泄漏时,提出裂缝微通道的表面粗糙度不应被忽略泄漏,郭红等[25]通过试验发现改善表面特性可大大降低动压轴承的摩擦阻力和摩擦系数.
综上所述,不论是气体密封还是其他机械零部件,摩擦副表面的真实形貌在特定情况下不应被完全忽视.本文中基于浮动式箔片气膜密封摩擦副配合表面粗糙微结构的分形特点,利用三维分形W-M函数模型描述形貌特征,考虑库伦摩擦效应和箔片的刚度及阻尼,建立三角形织构化的浮动式箔片气膜密封流体动力润滑方程,分析不同转速下楔形间隙气膜场及压力分布情况,并通过改变特征尺度系数和分形维数,进一步分析真实表面特性与静态和动态密封性能的相关性,为研究微观形貌对浮动式箔片气膜密封的影响提供一定理论依据.
1 几何结构模型
图1所示为浮动式箔片气膜密封结构,主要元件有密封腔体、刚性转轴和弹性密封面.刚性转轴偏心安装在密封腔内,弹性密封面主要由弹性波箔片和支撑平箔片组成,平箔片延伸至密封腔外并压紧固定,波箔片与平箔片和密封腔体分别接触,并在载荷作用下发生滑移和结构变形,如图2所示.
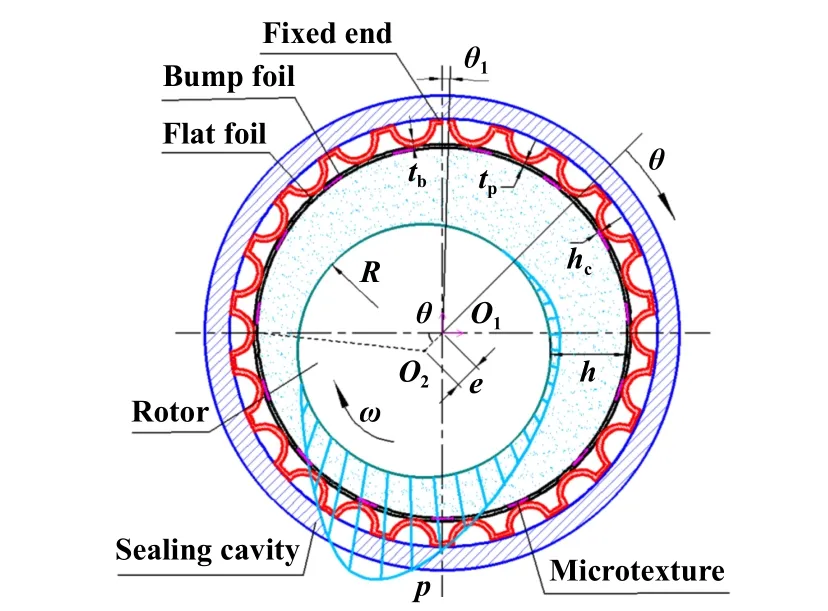
Fig.1 Schematic diagram of floating foil gas seal图1 浮动式箔片气膜密封结构示意图
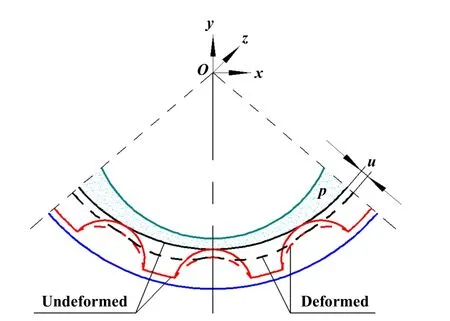
Fig.2 Deformation of the elastic sealing surface图2 弹性密封面的变形
图1和图2中,θ1波箔片两端形成的角度(°);p为气膜压力(Pa);h为气膜厚度(μm);tb和tp分别为波箔片和平箔片的厚度(mm);hc为织构深度(μm);e为偏心-距(mm);R为旋转轴外径(mm);O1和O2分别为密封腔和旋转轴的中心;u为弹性密封面的变形量(μm);ω为旋转角速度(rad/s);θ为圆周方向坐标(rad).
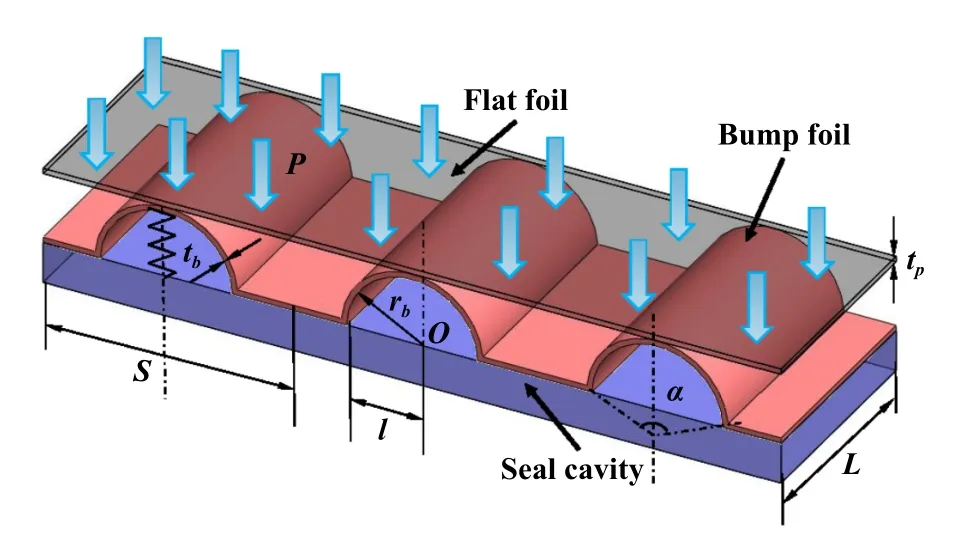
根据南洋[26]针对不同织构的分析,三角形作为具有典型“由宽至窄”形状的收敛型织构,可在流体流出织构时实现较大的额外增加作用,因而本文中参考其研究结果在平箔片表面设计三角形织构,如图3所示,图3中L为密封宽度(mm);a为三角形的边长(mm).

Fig.3 Textured surface of flat foil图3 平箔片的织构化表面
2 数学理论模型
2.1 数学理论模型
本文中假设弹性顶层平箔片表面为粗糙表面,刚性转轴表面为光滑表面,如图4所示.

Fig.4 Sealing gap considering micro-topography图4 考虑微观形貌的密封间隙
在分形理论中,粗糙表面的微观轮廓是连续和处处不可微的,且具有自相似性.本文中采用较为成熟的W-M三维模拟函数[27]表征各向同性的分形粗糙表面,表达式如式(1)所示.
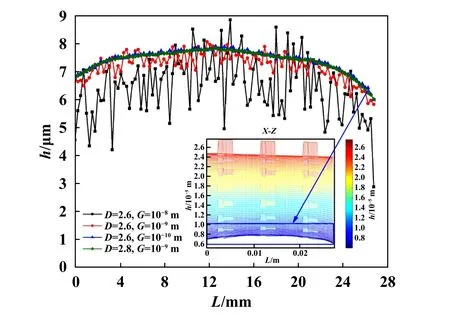
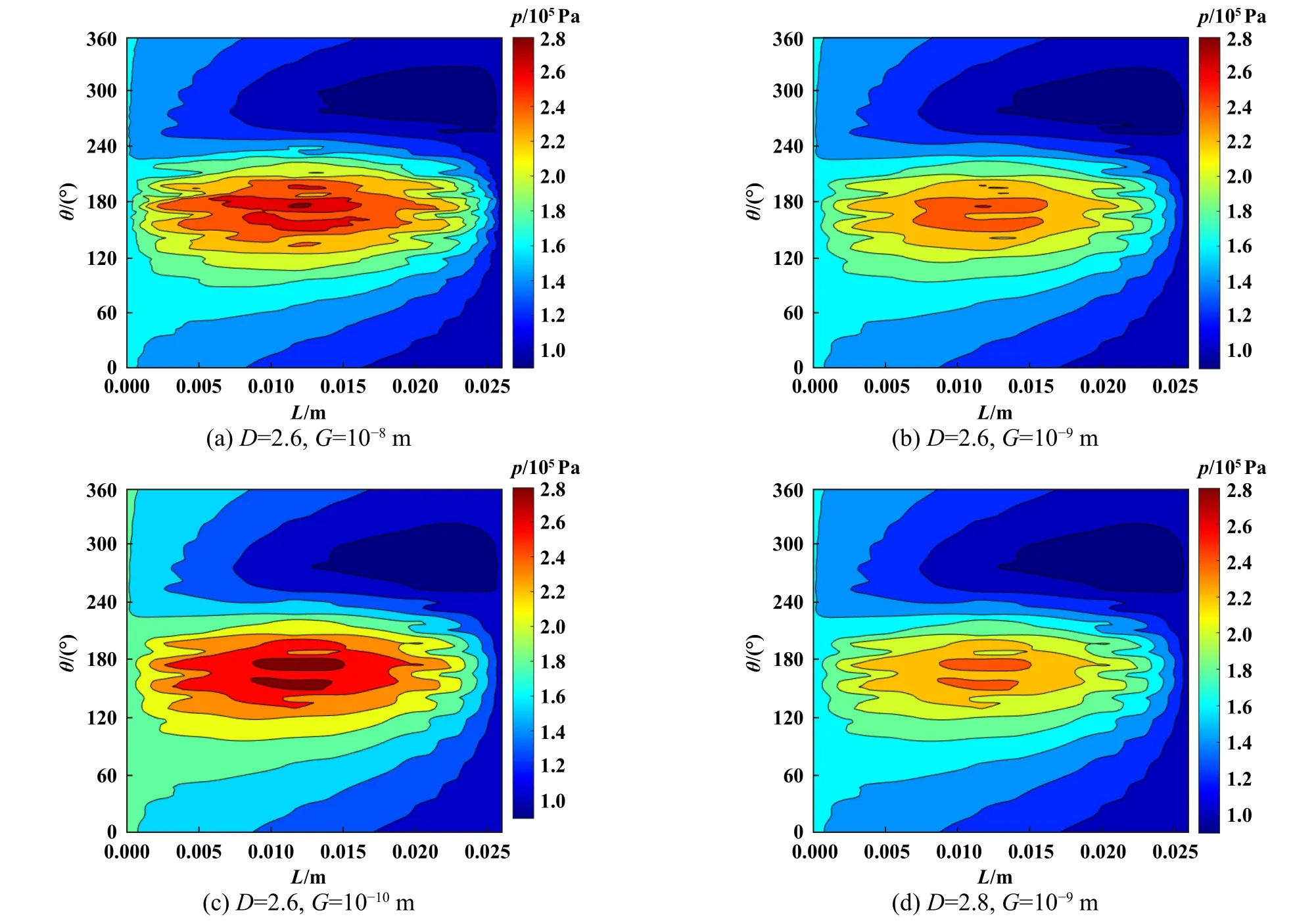
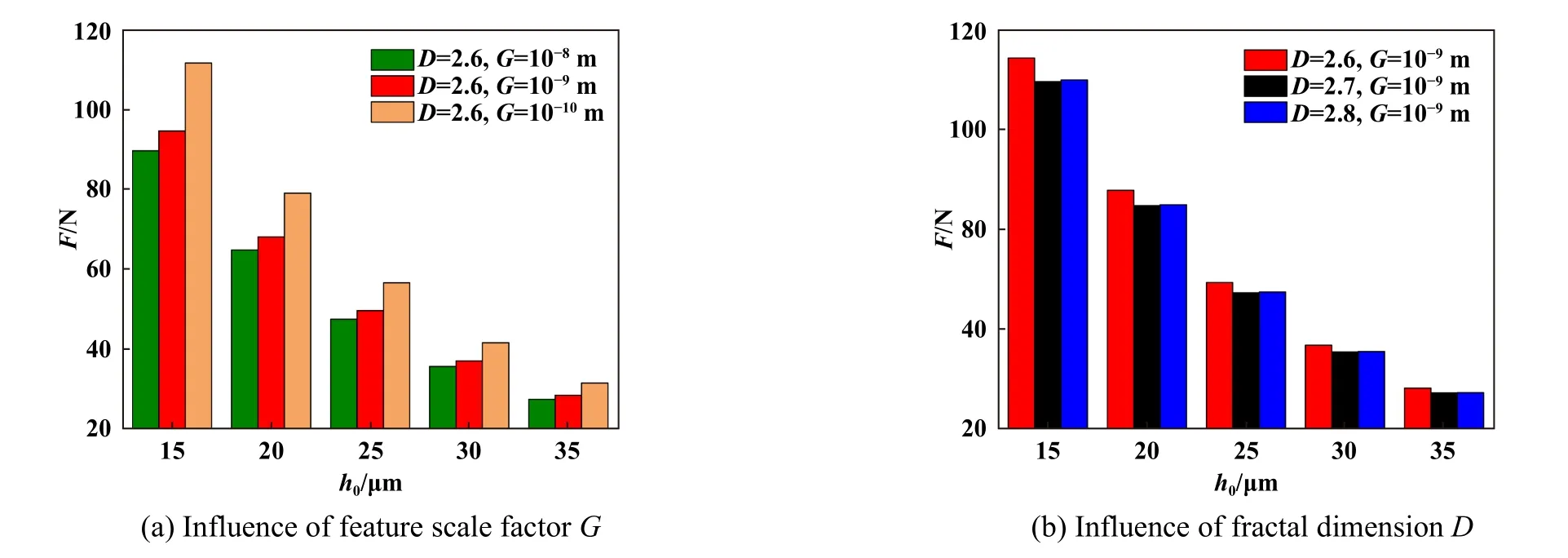
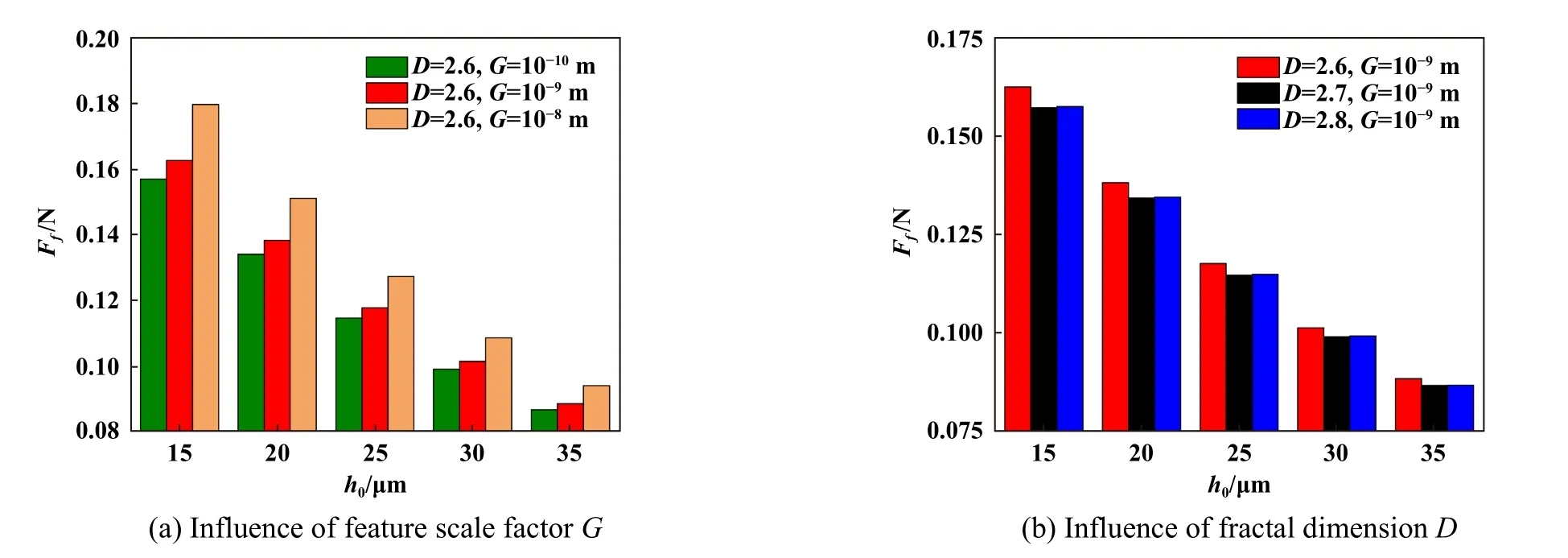
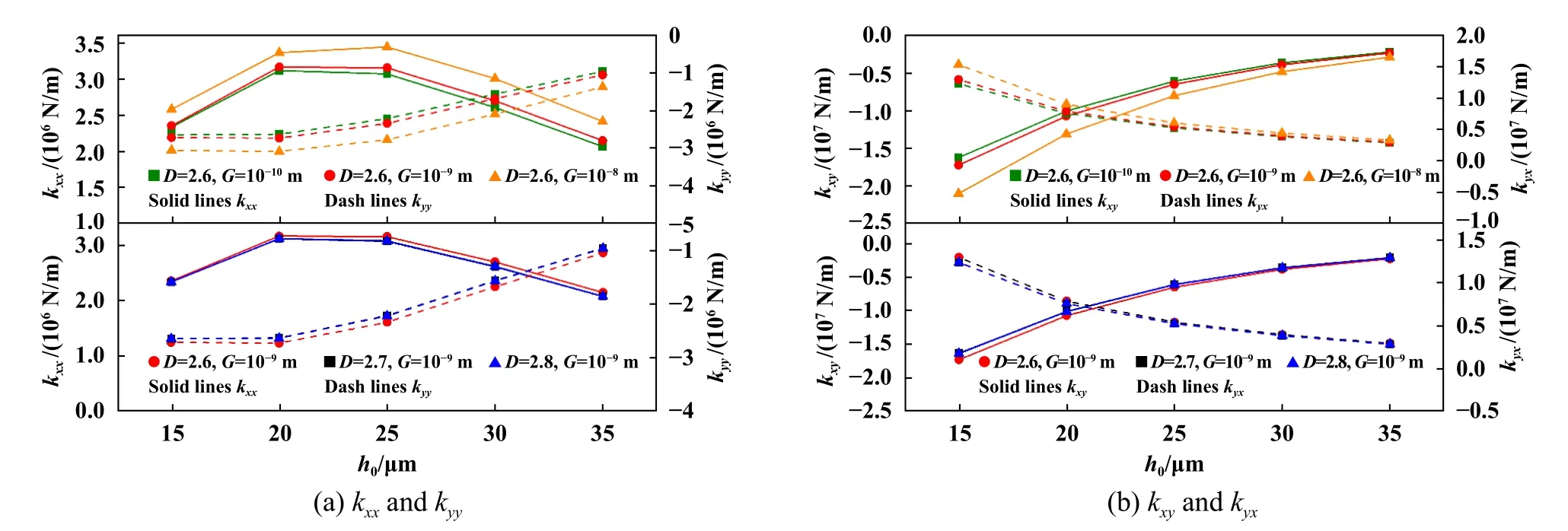
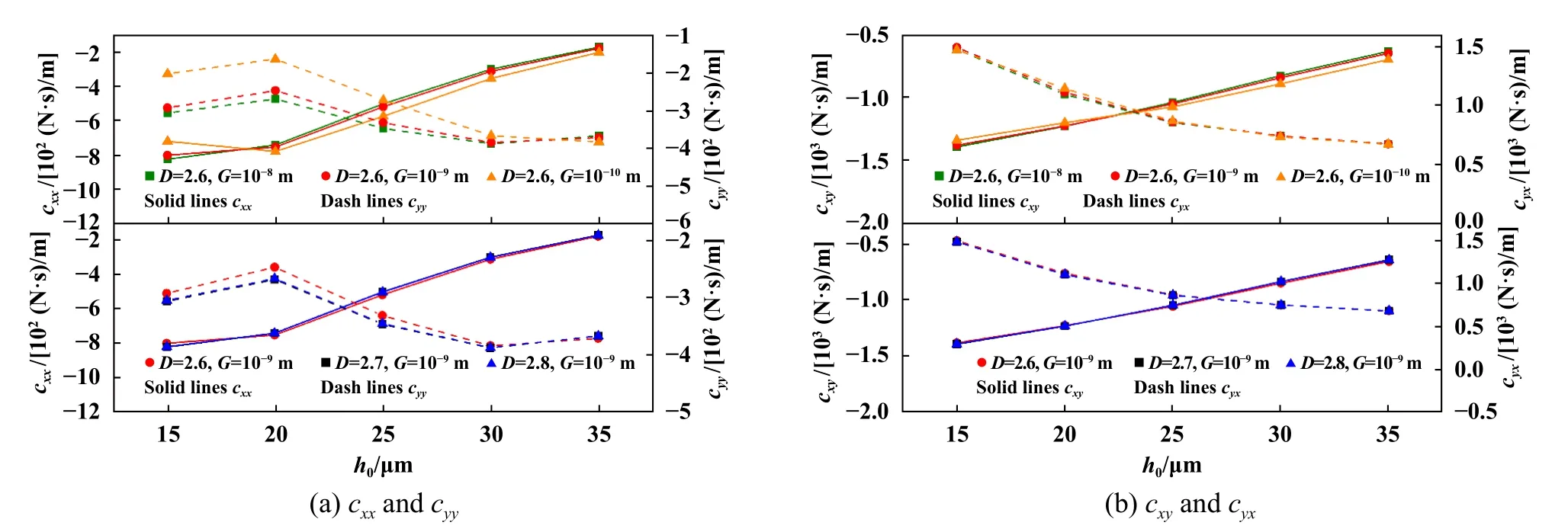
式中,hs为任意一点粗糙表面上的高度;(x,y)为位置坐标;L'为取样长度(m);G为特征尺度系数(m);Γ (Γ>1)为确定频率密度的相关函数;nmax为最高频率系数,其中Ls为截止长度(m);M为曲面褶皱的重叠数;m和n均为频率系数;γ为随机轮廓的空间频率,其值大于1;D(2 图5所示为弹性密封面的结构参数,rb为波箔片半径,s为波箔片节距,l为波箔片弦长的一半,α为波箔片包角. Fig.5 Structural parameters of elastic sealing surface图5 弹性密封面的结构参数 一端固定的波箔片的刚度计算式[28]如下: 式中,J是波箔片角度α与摩擦系数μf有关的函数;kb为波箔片刚度(N/m3);tb为波箔片厚度(mm);μf为波箔片与密封环之间的摩擦系数;νb为波箔片泊松比;Eb为波箔片弹性模量(GPa). 假设密封介质为理想气体,气体特征不发生变化,流场为层流,流体和固体间无滑移,可以得到适合浮动式箔片气膜密封的动态压力控制方程如式(3). 由于织构的面积很小,本文中假设织构区域和非织构区域的表面特性相同.结合公式(1)和公式(2),得到静态气膜厚度公式(4). 无量纲参数定义为 式中,z为轴向坐标(m);t为运动时间(s);h0为平均气膜厚度(μm);hc为任意一点粗糙峰的高度(μm);τ为涡动角速度(rad/s);pa为出口压力(MPa);μ为润滑气体的黏度[(N·s)/m2];γ为扰动比;Λ为可压缩系数;ε为偏心率;P、Z、H、T、Hc和Kb分别为p、z、h、hc和kb对应的无量纲参数. 平衡位置受到 ( ∆x,∆y) 的位移扰动和的速度扰动后,得到无量纲扰动量 将气膜厚度、气膜压力和箔片变形量均在平衡位置处进行Taylor级数展开. 将(7)式带入(3)式,并忽略高阶小量进行计算. 在以上公式中,下标x和y分别为坐标方向; ∆x和∆y分别为平衡位置受到的小扰动量, ∆X和 ∆Y分别为对应的无量纲数值;和分别为平衡位置受到的扰动速度,和分别为对应的无量纲数值;U为弹性密封面的无量纲变形量,Px、P′x、Py和Py′为P的扰动量,Hx、Hx′、Hy和Hy′为H的扰动量,Ux、U′x、Uy和Uy′为U的扰动量. 考虑时间项后,气膜厚度偏离静态气膜厚度H,得到微扰下的气膜厚度 扰动后气膜厚度和箔片变形量之间的关系为 根据气膜压力和波箔片的变形关系式,可得: 将式(7)和式(9)带入式(10),可得: 式中,Ut为无量纲径向变形量,Cb为箔片的无量纲阻尼. 由于x方向和y方向的动力学系数的求解过程独立,下面以x方向的求解为例,通过(11)式可得: 将计算得到的公式(13)带入到3.3小节获得的公式中,展开各项并合并同类项,并将方程改为差分格式进行计算. 在密封面的进出口设置强制性边界(14),在中截面位置设置循环边界(15). 评价浮动式箔片气膜密封的关键静态特性参数有气膜浮升力F,质量泄漏率Q,偏位角β以及摩擦力Ff,公式中下标h和v分别代表水平方向和竖直方向. 直接刚度系数kxx和kyy,直接阻尼系数cxx和cyy,交叉刚度kxy和kyx,交叉阻尼系数cxy和cyx为浮动式箔片气膜密封稳定性的关键参数,可以表示为 对离散后的求解方程采用超松弛迭代法进行计算,并依据气膜压力和气膜厚度的收敛条件对二者同时进行判断,具体计算流程如图6所示.图6中,nr为旋转速度(r/min),pi为进口压力(MPa). Fig.6 Calculation flow chart图6 计算流程图 本文中计算时所采用的浮动式箔片气膜密封几何结构与力学性能参数列于表1中,工况参数列于表2中. 表1 浮动式箔片密封的几何形状和力学性能Table 1 Geometry and mechanical propertiesof floating foil gas seal 表2 浮动式箔片密封的运行条件Table 2 Operation conditions of floating foil gas seal 刚性浮环密封即浮动式箔片气膜密封中弹性密封面不发生变形的情况,计算时可将密封面刚度设为无穷大来达到此目的,因而可以选择文献[29]中双列一字平行槽柱面密封的结构参数的研究成果验证.经过计算得到的压力分布如图7(a)所示,当气体流动至动压槽时压力上升,并在槽根附近达到最大值,之后压力沿着流动方向逐渐减小,该现象与文献[29]具有较好的一致性.不同转速条件下气膜浮升力和质量泄漏率的对比结果如图7(b)所示,通过对比发现,本文中气膜浮升力与文献[29]中理论值的最大和最小误差分别为11.60%和0.97%,与文献[29]中试验值的最大和最小误差分别为12.56%和0.45%.本文中的质量泄漏率与文献[29]中的理论值几乎一致,最大和最小误差分别为2.38%和0.25%,与文献[29]中试验值的最大和最小误差分别为16.65%和10.27%,以上分析说明本文中使用的计算方法具有一定可靠性. Fig.7 Calculation program verification图7 计算程序验证 由图8可知,在一定范围内改变描述表面形貌的分形参数,气膜厚度的整体趋势并不会发生改变,均沿θ=180°呈轴对称分布,且微织构区域气膜厚度明显较大.图8(a)、(b)和(c)为不同特征尺度系数G下的浮动式气膜密封的气膜厚度分布,对比发现,特征尺度系数G越小,粗糙表面的高低起伏程度也越平缓.分形参数D保持2.6不变,当G=10-8m时,对应的最大粗糙峰高度为3.37 μm,当G=10-9m时,对应的最大粗糙峰高度为1.55 μm,说明特征尺度系数G越小,对应的粗糙峰高度越小,密封副表面也就越平整.观察图8(b)和(d)中不同分形维数D下的气膜厚度分布可以看出,分形维数D越小,表面轮廓的变化越复杂,表面就越粗糙. Fig.8 Gas film thickness distribution under different fractal parameters图8 不同分形参数下的气膜厚度分布 不同于刚性浮环密封气膜厚度几乎不发生变化的情况,浮动式弹性箔片密封的气膜厚度受到密封面变形和气膜压力的影响,为方便观察,提取在θ=180°位置处的气膜厚度,并结合D=2.6和G=10-9m时x-z方向的气膜厚度分布进行分析,如图9所示,当流体从压力进口处流至压力出口处时,在θ=180°位置的气膜厚度呈现出先增大后减小的变化趋势,其中最小的气膜厚度出现在压力出口处,这是由于此处的压力值为环境大气压,密封面不发生变形. Fig.9 Gas film thickness distribution at θ=180°图9 θ=180°位置处的气膜厚度分布 同时,得到与图9对应的气膜压力分布,如图10所示,类似地,气膜压力的演变规律并没有随着一定范围内分形参数的改变而发生大幅变化,但图10(a)、(b)、(c)和(d)的压力数值不同,对应的最大气膜压力分别为0.28、0.26、0.26和0.25 MPa.当密封介质以进口压力流入微间隙后,气膜压力先增大,后随之减小至出口压力,并均在θ=180°、L=12.57 mm附近出现了较大气膜压力,结合图9的气膜厚度数据分析可知,该位置的气膜厚度较大,即较大的压力导致了密封面较大的变形,因而气膜厚度相较于初始状态明显增大.此外,在高压区域一侧靠近出口的位置均出现了负压,但不同分形参数下的最小气膜压力均接近0.09 MPa.由于表面形貌的不同和微织构的存在,气膜的等压线出现了不同程度的规律波动,可以看出,平箔片越粗糙、坐标位置越接近θ=180°的轴对称位置,气膜压力的伏动越剧烈. Fig.10 Gas film pressure distribution under different fractal parameters图10 不同分形参数下的气膜压力分布 不同分形参数下的气膜浮升力变化如图11所示.随着平均气膜厚度的增大,流体动压效应减弱,气膜浮升力随之减小,但在同一平均气膜厚度下,随着特征尺度系数G的增大,气膜浮升力均呈现出不同程度的增长趋势.当平均气膜厚度为15 μm,特征尺度系数G从10-10m增大至10-8m时,气膜浮升力增大了24.56%,当分形维数D从2.8减小至2.7时,气膜浮升力降低了5.00%,但当分形维数D从2.7减小至2.6时,气膜浮升力反而增大了0.29 N.可见特征尺度系数G对气膜浮升力的影响单调唯一且更加显著,导致这种计算结果出现的原因主要是特征尺度系数G的倍数增大,意味着曲面的粗糙峰值范围也呈倍数增大.对应前文中的分析可知,密封副表面的粗糙峰越大,对提升气膜浮升力越有利,但考虑到过大的粗糙峰值也会造成转子和平箔片表面的摩擦磨损,应适当降低表面粗糙度. Fig.11 Variation of gas film force图11 气膜浮升力的变化 平均气膜厚度和分形参数对质量泄漏率的影响如图12所示.特征尺度系数G在图12(a)中的范围内减小,平均气膜厚度分别取值15和35 μm时,质量泄漏率分别增长了20.44%和8.36%,同理可得出分形维数D从2.6增大至2.7时,平均气膜厚度取值分别15和35 μm时,质量泄漏率分别增长了4.65%和1.99%,之后分形维数D的增大基本不会引起质量泄漏率的变化.明显地,平均气膜厚度增大,大大削弱了表面形貌对质量泄漏率的作用程度,且粗糙的表面形貌可有效控制密封的泄漏.相较于密封副形貌的影响,平均气膜厚度是决定质量泄漏率更为关键的决定因素,这主要是因为平均气膜厚度增大使得泄漏间隙急剧扩大. 由图11分析可知,平均气膜厚度增大,承载力减小,密封系统逐渐趋于不稳定状态,因而偏位角随着平均气膜厚度的增大快速增大,如图13所示.以平均气膜厚度为20 μm为例,特征尺度系数G取值10-10、10-9和10-8m时,对应的偏位角分别为41.22°、39.93°和35.57°,分形维数D取值2.6、2.7和2.8时,对应的偏位角分别为39.93°、41.17°和41.09°;以平均气膜厚度为30 μm为例,特征尺度系数G取值10-10、10-9和10-8m时,对应的偏位角分别为54.89°、53.88°和50.42°,分形维数D取值2.6、2.7和2.8时,对应的偏位角分别为53.88°、54.85°和54.78°.对比可以发现,相较于分形参数对偏位角的影响,平均气膜厚度对偏位角的影响更大,且特征尺度系数G趋于较小值,分形维数D趋于较大值,其变化对偏位角的影响能力会逐渐减弱,这是因为此时密封面逐渐趋于光滑表面,分形参数的变化不再影响表面形貌的大幅变动. 如图14所示,其他条件不变,气膜厚度增大,气膜厚度方向的速度梯度减小,因而黏性摩擦力减小.此外,黏性摩擦力与流体通道的壁面光滑度息息相关,不同的特征尺度系数G意味着曲面幅度不同,当介质流过密封通道时,流体状态会因壁面的突变而发生改变,随之流体自身的黏性会牵制这种改变的发生而产生较多摩擦力,当特征尺度系数G越小,流道壁面粗糙峰越大,这种现象发生得越频繁,流体层间的剪切率越高,摩擦力也就越大.不同的分形维数D意味着曲面密集度不同,当分形维数D从2.6增大至2.8时,黏性摩擦力先增大后减小,说明曲面密集度单调变化对黏性摩擦力的影响并不规则. Fig.14 Variation of friction force图14 摩擦力的变化 图15所示为动态刚度系数随平均气膜厚度的演变规律.通过观察看出,浮动式箔片气膜密封的直接刚度系数kxx在气膜厚度较小时先增大,当气膜厚度超过25 μm后不断减小,而直接刚度系数kyy呈现出单调递增的趋势.交叉刚度系数kxy在负值范围内单调增大趋近于0,kyx在正值范围内单调减小趋近于0,二者的变化规律近似对称.交叉刚度值一正一负,二者的差值为正值,且随着气膜厚度的增大,交叉刚度的差值越大,表示对涡动做的正功越多,密封系统失稳的可能性越大.当分形维数D从2.8减小至2.7时,动态刚度系数几乎不发生变化,而当特征尺度系数G增大或分形维数D从2.7减小至2.6时,动态刚度系数的波动幅度较大,因而密封系统有更大的不稳定可能性,即表面粗糙峰越大,密封系统越倾向于不稳定状态. Fig.15 Variation of dynamic stiffness coefficient图15 动态刚度系数的变化 直接阻尼系数与直接刚度系数的变化趋势相反,如图16所示.一般情况下,气膜厚度减小,气膜承载力增大,气膜刚性随之加强,因而导致气膜的阻尼效果不充分.直接阻尼系数cxx和cyy在图16(a)中存在极值,由于x方向承担了较多的载荷,结合图16(a)分析,说明在气膜厚度为20 μm附近存在较好的稳定性.进一步观察看出,增大气膜厚度削弱了分形参数的变化对动态阻尼系数的影响,甚至当气膜厚度超过30 μm时,分形参数对动态阻尼系数可以忽略不计. Fig.16 Validation of dynamic damping coefficient图16 动态阻尼系数的变化 通过W-M分形函数模拟了浮动式弹性箔片气膜密封摩擦副的三维粗糙表面,并构建了考虑波箔片刚度和阻尼的微尺度动力润滑方程,并耦合求解得到以下结论: a.一定范围内的分形参数变化并不会影响气膜厚度和气膜压力的整体分布规律,但当平均气膜厚度较小、表面粗糙峰波幅较剧烈或伏动较密集时,分形参数对密封性能的影响不可忽略. b.针对计算工况,当特征尺度系数G在10-10~10-8范围内增大或分形维数D在2.7~2.6范围内减小时,可有效增强气膜浮升力和控制质量泄漏率,但对降低黏性摩擦力和提高密封系统稳定性是不利的,但当分形维数D大于2.7时表现出相反的影响趋势. c.动态特性系数随着气膜厚度的变化呈现出较为复杂的变化趋势,但随着气膜厚度增大,密封系统越倾向于不稳定状态,并在气膜厚度为20 μm附近表现出最佳动特性.2.2 波箔片刚度模型
2.3 雷诺方程和小扰动法
2.4 气膜压力与箔片变形和气膜厚度的关系
2.5 气膜压力与箔片变形和气膜厚度的关系
2.6 密封性能参数
2.7 收敛条件与计算流程
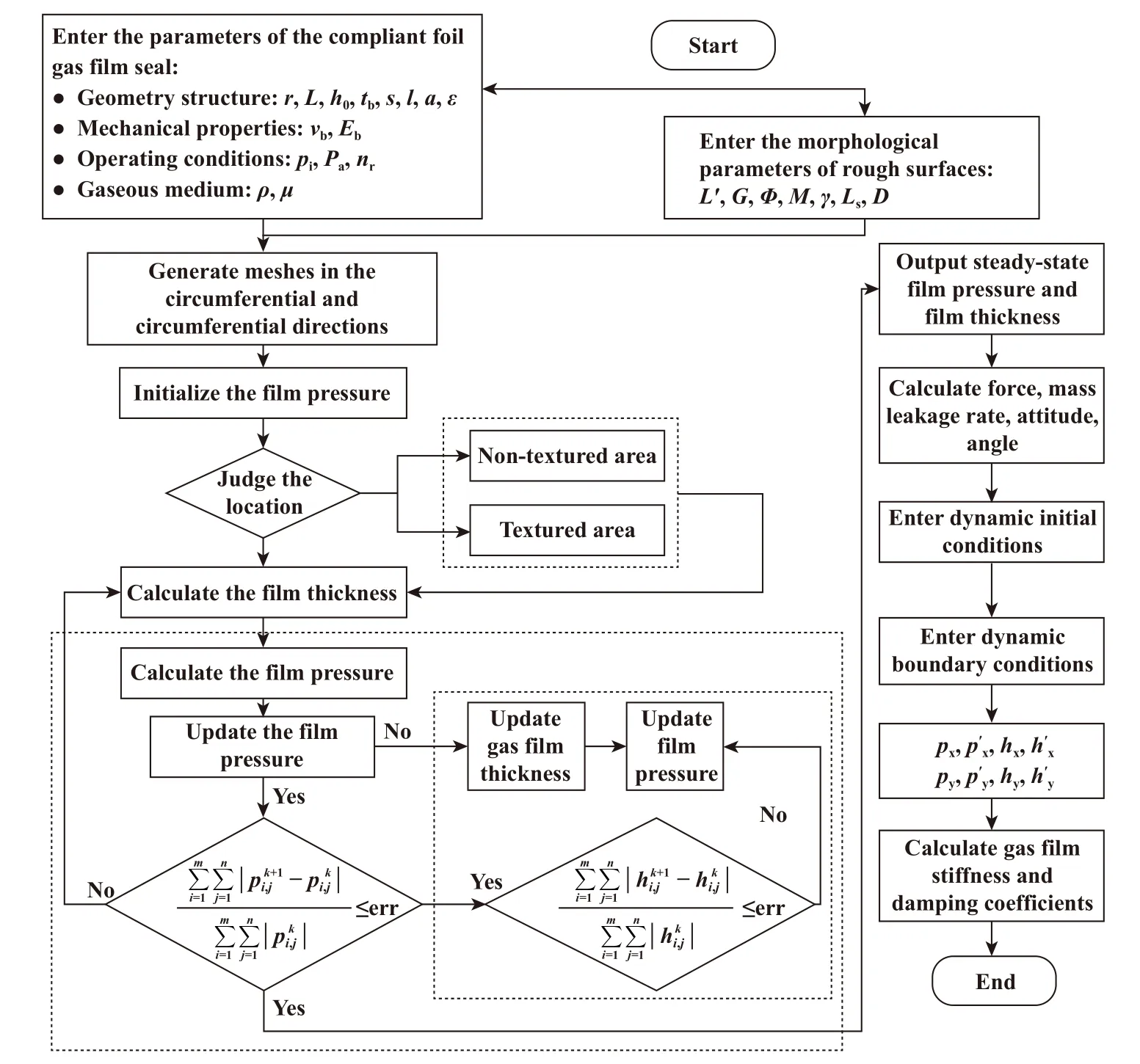
3 参数选取
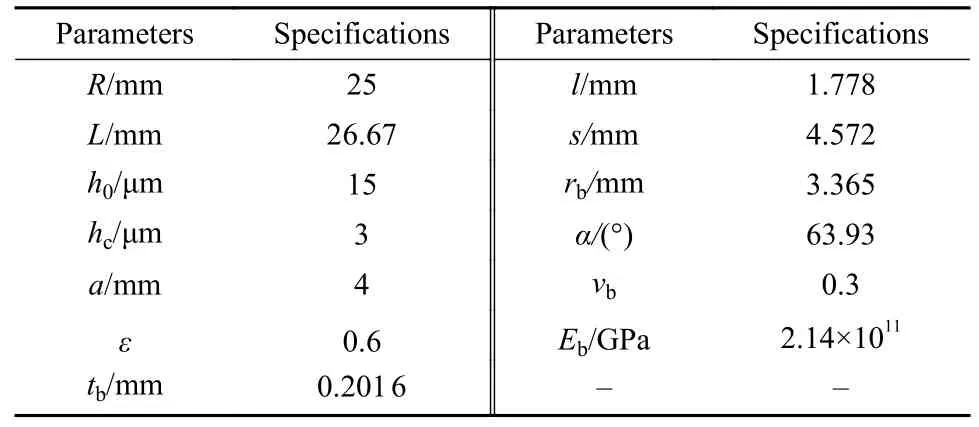
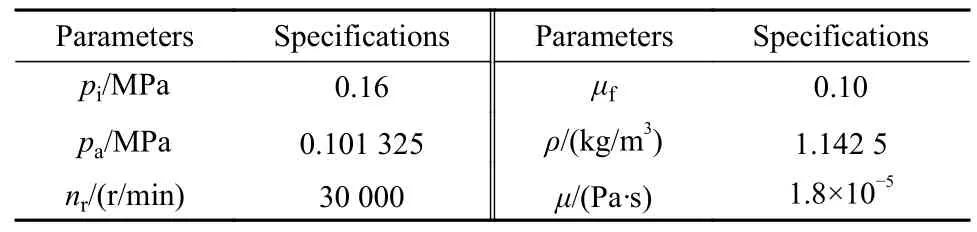
4 程序正确性验证
5 结果讨论与分析
5.1 不同分形参数下的气膜厚度和气膜压力分布
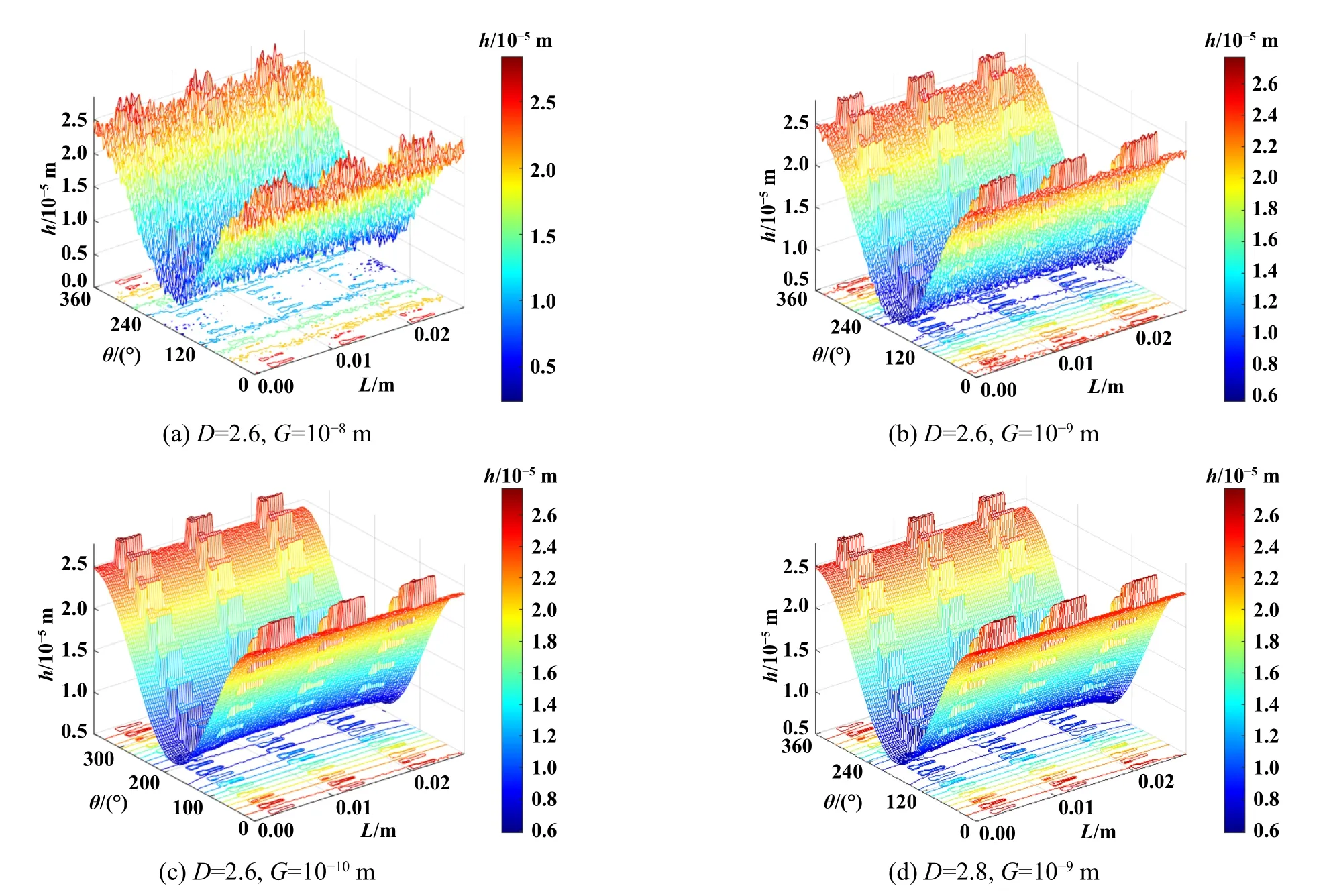
5.2 不同分形参数下的静态密封特性变化
5.3 不同分形参数下的动态密封特性变化
6 结 论

