新型自冲击密封的泄漏特性与封严机理初探

王 衍, 黄周鑫, 何一鸣, 刘佳利, 王一钦, 刘 威, 金旭成

(江苏海洋大学 机械工程学院，江苏 连云港 222005)

各类旋转机械运行过程中，泄漏问题普遍存在，其结果往往会造成设备停车、能源浪费、环境污染甚至危害人身安全，带来巨大的经济损失.如何防止泄漏一直是各类高端装备领域的重要课题，相关密封技术研究显得极为重要.最新API-682标准[1]规定密封系统须至少连续稳定运行3年(25 000 h)以上，基于流体动压润滑的非接触式流体密封技术具有零泄漏、低功耗及长寿命等特性，发展异常迅猛，国内外已经将高性能非接触式流体密封作为先进密封技术研发的重点方向[2-3]，实现此类密封的高效稳定运行一直是高端机械领域的热点课题之一.

目前，非接触式流体密封主要包括间隙密封、螺旋密封、迷宫密封和端面密封等.间隙密封凭借零磨损、寿命长、运维简单以及成本低等优势广泛应用于以液压缸为代表的各类设备中[4-5]，适用于气体和液体环境，但整体泄漏较大.螺旋密封是本世纪才迅猛发展起来的一种新型非接触密封技术，主要应用于水泵、压缩机和发电机中[6-7]，顾永泉[8]通过分析螺旋密封的基本结构系统阐述了其工作原理，并建立了密封封液能力公式。阿达依·谢尔亚孜旦[9]将螺旋密封等同为4杆机构，建立了密封公式并对螺旋密封“气吞”现象及其机理进行了分析。周志安[10]进一步修正了密封公式中的泵送速度和缝隙流量，并对其中的其他参数进行了优化.

20世纪80年代，我国民航使用的MK-152发动机曾因滑油消耗过大而导致提前更换，改用迷宫密封后油耗量直接下降了40.7%[11].90年代美国国家航空航天局(NASA)实施的AST (Advanced subsonic technology)计划表明，航空发动机燃油率每降低10%，其中2%~3%来自对迷宫封严技术的改进[12].我国新型战斗机的发动机实际应用也表明，通过合理改善迷宫密封的封严性能，其工作效率可显著提升10%[13].基于动静压原理的端面密封技术[14]具有低磨损、长寿命和零泄漏等特性，主要包括干气密封、液膜密封及上游泵送密封等.上世纪60年代，美国国家航空航天局(NASA)、普惠航空(PWA)及通用电气(GE)已开始探求将干气密封用于航空发动机的高滑速关键部位[15].单套干气密封受透气效应影响无法实现零泄漏，实际多采用密封组合方式，且密封正常运行气膜厚度仅为2~5 μm[16]，介观尺度气膜和系统的稳定性不容乐观；而且，干气密封的核心技术[17]在于3~10 μm槽型的精密加工表面粗糙度(Ra)<0.8 μm，此类高效精密制备方法也一直是国内技术短板.上游泵送密封多用于液相介质，源自气体润滑轴承技术，1981年，首个上游泵送密封专利技术获批，20世纪90年代以来，对这一技术的研究逐渐增多，形成了系列产品并在工业中成功应用[18].

综上可知，非接触式流体密封仍然存在许多不足：(1) 迷宫、干气、螺旋和间隙密封等密封形式存在直通型透气效应，致使泄漏大及封严效率低；(2) 干气、离心、螺旋和上游泵送密封等过分依赖主轴转速，启动停车阶段会失去密封能力；(3) 干气、上游泵送和螺旋密封等辅助装置复杂、系统稳定性较差.虽然存在一定的不足，但无固相磨损的非接触形式仍不失为高工况下先进密封技术的发展方向，如能进一步通过创新流体阻塞机制，提高封严效率、避免对转速的依赖，将使非接触密封技术焕然一新.

1 新型自冲击密封的提出

作者所在课题组借鉴平面特斯拉阀结构及其被动式流体阻塞原理提出了1种新型自冲击非接触式流体密封结构[19-20]，为提高非接触式流体密封的整体性能提供了1种全新封严形式[21-22]，其基本结构如图1所示.可以看出，自冲击密封的结构设计非常简洁，层叠式结构具有极高的级数布置效率，主体仅包括外环、悬柱和内环3个部分.关键部件悬柱根据其置于内环或外环而分别转动或静止，每个悬柱缠绕一定厚度(依据具体密封间隙而定)和数量的窄边锡箔材料，即可压入相应内外环槽内卡紧，实现有效定位.理论上讲，高压介质进入这一结构后会被逐级节流降速，当级数足够多时，即可实现密封介质的零泄漏.课题组研究表明，新型密封具备的自冲击阻流形式，其节流效率显著高于间隙、螺旋和迷宫密封等具有显著直通效应的非接触密封形式；以密封间距为指标，新型密封实现标准泄漏时的密封间距是干气密封十几倍甚至几十倍，且新型密封间距为刚性间隙，稳定性更高.可见，自冲击型密封结构的提出，将衍生出1种密封新理论和原创技术，有助于实现对现有非接触密封体系的理论拓展和技术革新.

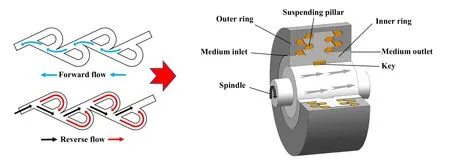
Fig.1 New Self-impact Seal Laminated type model图1 新型自冲击密封层叠式结构模型

自冲击密封以其独特的特斯拉阀型通道，借助流场中流体的自我冲击实现动能到内能的转换，进而达到能量耗散实现封严的目的.具体来看，其内部流场复杂，具有冲击、摩阻和流束收缩等形式.进一步揭示自冲击密封封严机理是推进此类密封进入实际应用的关键，本文中研究了进口压强、交错比和密封间隙对自冲击密封熵增以及泄漏量的影响规律，从热力学角度对自冲击密封流场特性和泄漏特性进行了分析，揭示了自冲击密封封严机理，为自冲击密封结构优化设计及实际开发应用提供理论依据.

2 基于热力学效应的泄漏量理论分析

2.1 密封热力学焓理论

自冲击密封内气流在进出口压差的作用下从高压处流向低压处.密封气流分析图如图2所示，取密封内的某段为研究对象，A和B分别表示气体经过密封时的某2个翼状的相同位置.从热力学效应角度来考虑，气体由位置A的状态量(Pa，Ta)经过流动后到达位置B，其状态量变为(Pb，Tb)，其中Pa和Pb分别表示气体在A和B位置处的压力，Ta和Tb分别表示气体在A和B处的热力学温度.

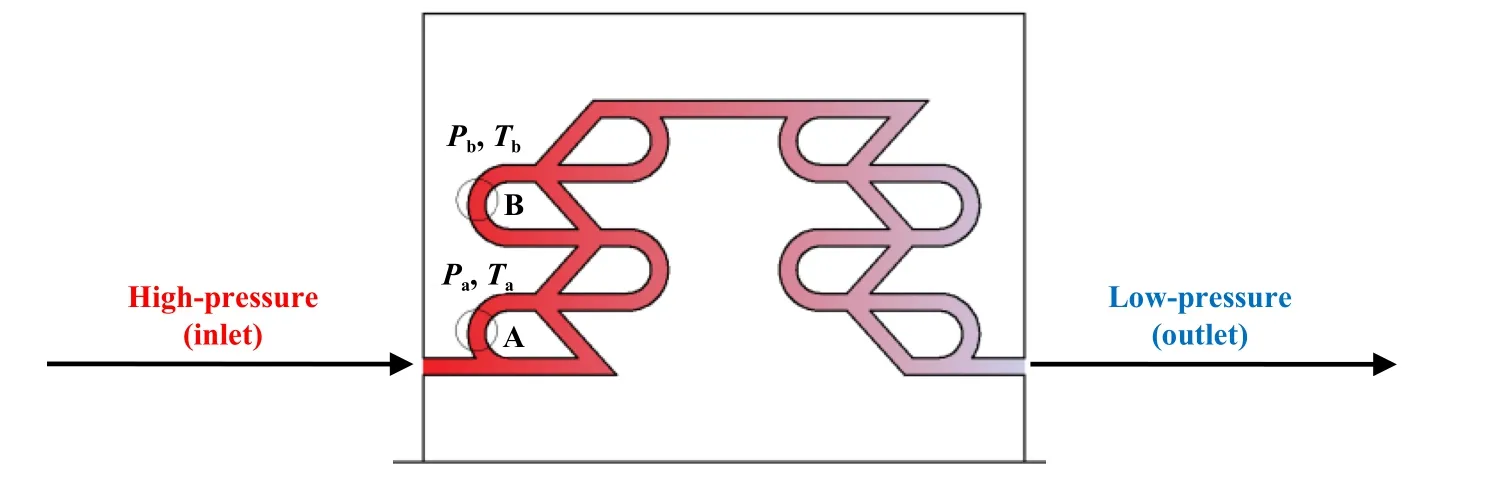
Fig.2 Sealing air flow analysis diagram图2 密封气流分析图

热力学中焓是表征物质能量的1个状态量，其反映的是系统所具有的能量.对密封气体来说，焓表示了气体所具有的热力学能和它所具有的推动功，焓增则表示气体从状态A变为状态B吸收的热量.由于密封腔内体积不变，气体所具有的热力学能为

式中，u为单位质量气体的热力学能；CV为单位质量气体的定容热容量，T表示热力学温度.

克拉贝隆方程如下：

式中，Rg=287 J/(kg·mol·K)，为理想气体常数，P为压强(Pa)，V为气体体积(m³).

密封内气体焓的表达式可定义为

式中，Cp为单位质量气体的定压热容量.

气体从位置A流动到位置B后，焓增为

式中，hb为气体在位置B的焓，ha为气体在位置A的焓.

2.2 密封热力学熵理论

熵描述的是内能与其他形式能量自发转换的方向和转换完成的程度.对密封内气体来说，熵增的大小反映了动能转换成热能的程度，熵增越少，气体热力学效应就越充分，密封封严效果就越好.气体从位置A流动到位置B后，熵增的值为

式中，dq为单位质量气体从位置A到位置B交换的热量；ds是此过程中单位质量气体的熵增.

由热力学第一定律，有

式中，dT表示温度的微小变化量，dp表示压力的微小变化量.

结合式(2)，密封内气流熵增的值为

积分式(7)得到位置A到位置B的熵增：

2.3 考虑热力学效应的密封泄漏计算

新型密封的冲击效应实际也是1种将密封流体的动能转换为热能的热力学过程，由此可采用Egli经验公式[23]计算自冲击密封泄漏量，公式如下：

式中，K为泄漏系数，A为密封间隙处的迎气面积；Ptot,in为气体进口总压；Psta,out为气体出口静压；Ttot,in为气体进口总温；n为自冲击密封级数.其中，修正系数K的确定是密封泄漏公式的关键.

由式(8)可知，在不考虑密封级间流动过程中的微小温度变化时，熵增的公式可简化为

将式(10)代入式(9)式中可得：

式(11)建立了熵增与泄漏量的关系，而熵增的大小反映了自冲击密封气体热力学效应的程度，因此可以通过此公式直观地反映气体热力学效应与泄漏量的关系.

3 自冲击密封数值求解模型

3.1 基本假设

特斯拉阀结构适用于低黏度流体[24]，密封介质选择空气.对密封流道模型作如下假设：

(1)新型密封流体为连续介质流动[25]，内部为湍流流场；

(2)流场中气膜的温度和黏度相等[26]；

(3)气体分子与润滑层管道壁面牢固吸附，无相对滑移；

(4)忽略密封通道变形对介质流动的影响；

(5)忽略气体重力的影响；

(6)密封管道内壁表面理论光滑.

3.2 控制方程及求解

采用ANSYS开发的Fluent软件对自冲击密封进行数值模拟，该结构为三维管流算例.定常不可压缩流体的控制方程可表示为如下通用形式：

式中，ρ为流体密度； ϕ为求解变量；u、v和w分别为轴向、径向和切向流体流动速度； Γϕ为扩散系数；Sϕ为源项.

边界条件选择采用强制性压力边界条件：入口处，有p=Pin(介质压力)；出口处，有p=Pout(大气压).

近壁区边界条件采用壁面函数法，压力与速度耦合方法为SIMPLE格式，选用k-ω湍流模型，通过中心差分对扩散项离散，对流项计算采用二阶迎风格式，连续方程和动量方程的迭代精度设为10-5，能量方程设为10-6.研究不同压比和密封间隙对自冲击密封熵增和泄漏量的影响规律，基本参数列于表1中.

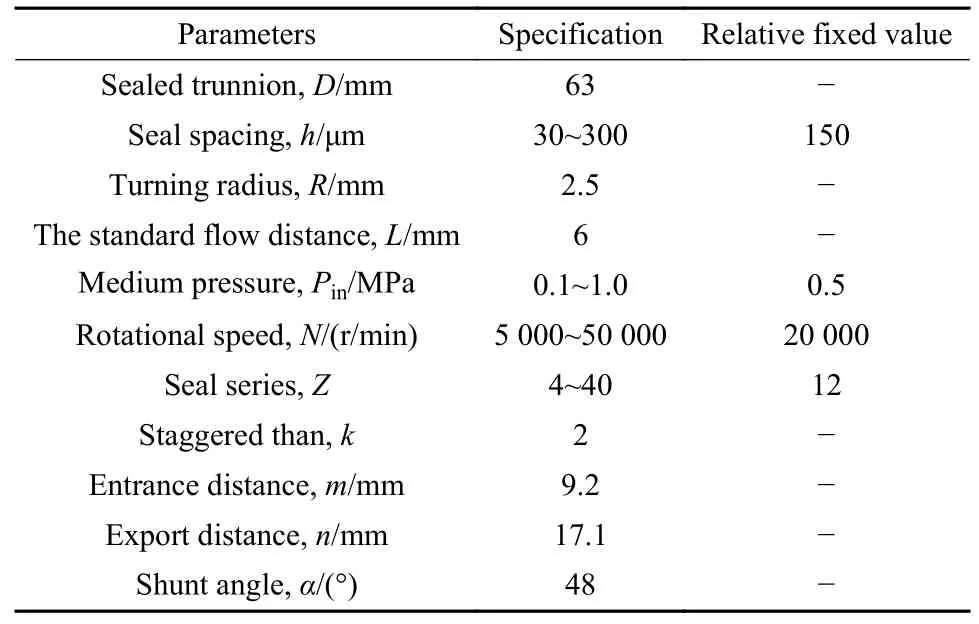
表1 自冲击密封几何参数Table 1 Self-impact Seal Geometric parameter

3.3 密封模型及网格无关性验证

自冲击密封的三维泄漏通道是基于平面特斯拉阀设计的，单级尺寸结构如图3右图所示，R为回转半径，L为流距，α为分流角，R、L和α三者存在互相制约的关系.模型中每个密封级尺寸一致，左侧为高压入口、右侧为大气侧低压出口.多个密封级串联起来共同组成自冲击密封三维泄漏通道.

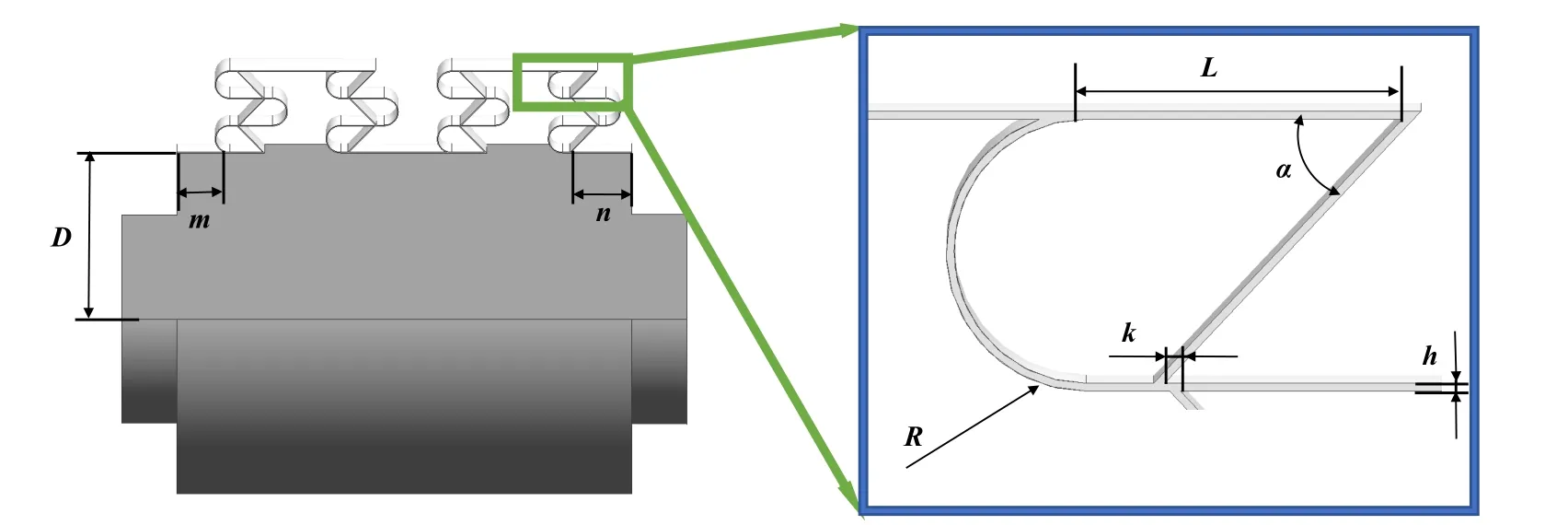
Fig.3 Self-impact Seal Dimension drawing图3 自冲击密封尺寸图

采用UG软件对自冲击密封进行全尺寸建模，然后导入Fluent meshing中进行网格划分，可以通过对Surface Mesh Controls系列参数包括Min size、Max size、Growth和Cells Per Gap的整体控制和调整，实现模型的网格划分及局部加密，网格划分效果如图4所示.

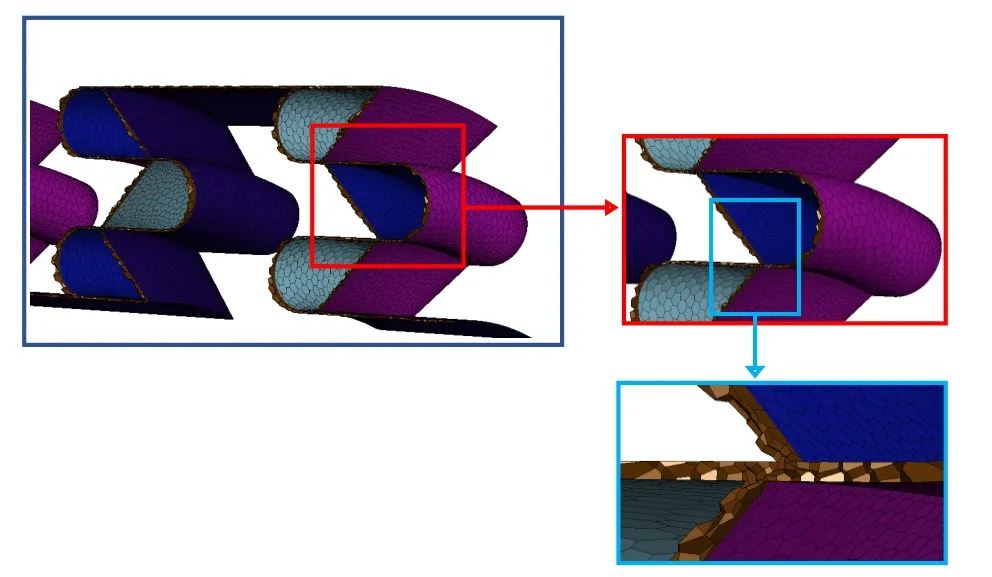
Fig.4 Sealing structure mesh model图4 密封结构网格模型

图5所示为网格无关性分析结果，从图5中可以看出泄漏量随网格数量的变化规律，随着网格数的增大，泄漏量减小且渐趋稳定，在网格数达到130万后趋于稳定.因此，后续计算中，兼顾计算精度和效率的要求，文中选取网格数量均在140万以上.

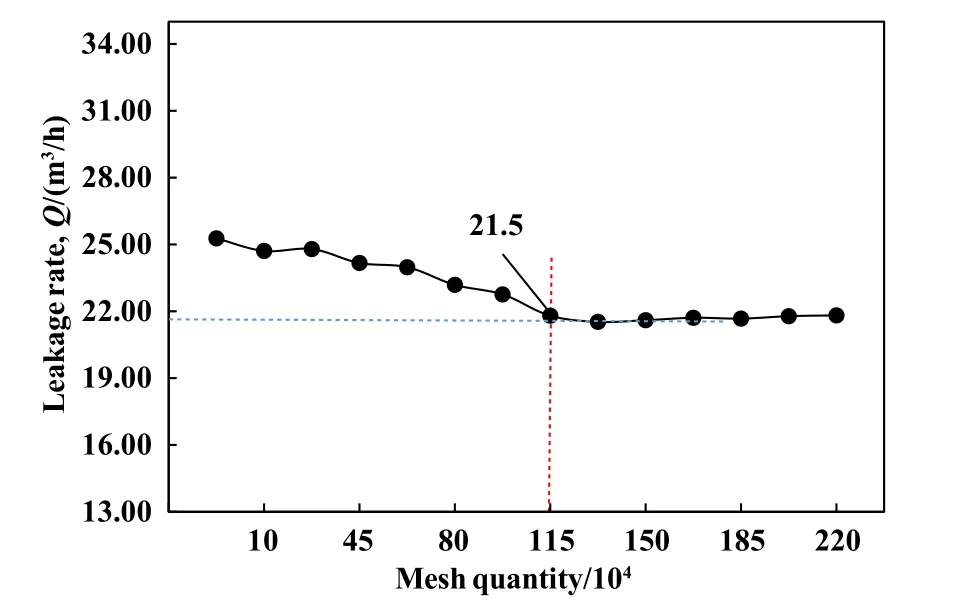
Fig.5 Effects of the mesh quantity on leakage图5 泄漏量随网格数量变化趋势

4 计算结果与分析

4.1 流场特性

4.1.1 压力特性

图6所示为自冲击密封不同位置对应的压力云图，可以看出，内部气体由高压端入口进入后，压力呈逐级降低的趋势，密封压降位于两级密封间的交汇处.流体间的冲撞、分叉形成的冲击阻塞效应在交汇位置表现最为强烈，这一位置也是压力能(动能)转化为热能的关键位置.此外，交汇位置的冲击还容易形成流体的漩涡和耗散不充分等情形，下文中的速度云图将更加清晰地显示这一现象.

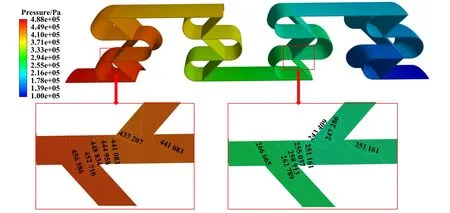
Fig.6 Pressure nephogram (Z=12; h=150 μm; N=20000 r/min; Pin=0.5 MPa)图6 压力云图(Z=12; h=150 μm; N=20000 r/min; Pin=0.5 MPa)

4.1.2 速度特性

图7所示为自冲击密封的速度矢量分布图，通过对冲击交汇位置进行局部放大可以看出，气流经过交汇位置时冲击异常剧烈，流体流速经冲击耗能以后整体呈降低趋势，动能转化为热能而耗散.每个交汇处的气体速度分布类似，交汇冲击位置的流速会出现短暂提升而后迅速降低，这是由冲击产生的自收缩效应所致.流体经过如此逐级冲击以后，动能逐渐减小，压差及流速也逐渐降低，进而实现节流抑漏的封严效果.

Fig.7 Velocity nephogram (Z=12; h=150 μm; N=20000 r/min; Pin=0.5 MPa)图7 速度云图(Z=12; h=150 μm; N=20000 r/min; Pin=0.5 MPa)

4.1.3 温度特性

图8所示为自冲击密封的温度变化云图，由图8可以看出，气流流经整个流道时的温度呈逐级上升趋势，温度变化规律符合前文中分析的动能转换为内能作用机制.温度的显著变化位置仍然位于交汇区域，而在通道内温度变化较小，进一步显示了交汇区域流体冲击的激烈程度.由温度云图还可以看出，最高温度位于串联层叠式结构的第3列处，原因是气体历经密封交汇处的层层阻隔，当进入第4列后，速度降至最低，使得位于翼状交汇处的冲击激烈程度减小，产生的热能减小，温度也随之降低.通过温度云图的局部放大图可以看出，越接近内环流道壁面，气流温度越高，这是由于内环为旋转部件，旋转时会产生一定的摩阻效应，使得贴近内环壁面的温度高于其他部位.

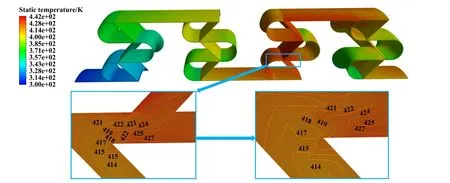
Fig.8 Temperature nephogram (Z=12; h=150 μm; N=20000 r/min; Pin=0.5 MPa)图8 温度云图(Z=12; h=150 μm; N=20000 r/min; Pin=0.5 MPa)

4.2 泄漏系数K的确定

Egli经验公式主要基于对流动过程的热力学分析、简化和假设，再通过某些计算方法而得到计算泄漏量，实际泄漏量则是需要通过“泄漏系数K”进行修正得到[27].目前，“泄漏系数K”一般都是根据特定的试验数据或者采用经验数值确定，本文中通过泄漏经验公式及数值仿真，分别计算自冲击密封的泄漏量.图9(a)所示为不同泄漏系数下经验公式与仿真结果的平均相对误差变化曲线，可以看到，当泄漏系数K=0.7时平均相对误差最小，二者计算结果最接近，故泄漏系数K取0.7.图9(b)所示为泄漏系数K=0.7时，基于不同密封级数下的泄漏公式和数值仿真的计算结果对比曲线，二者趋势符合较好.

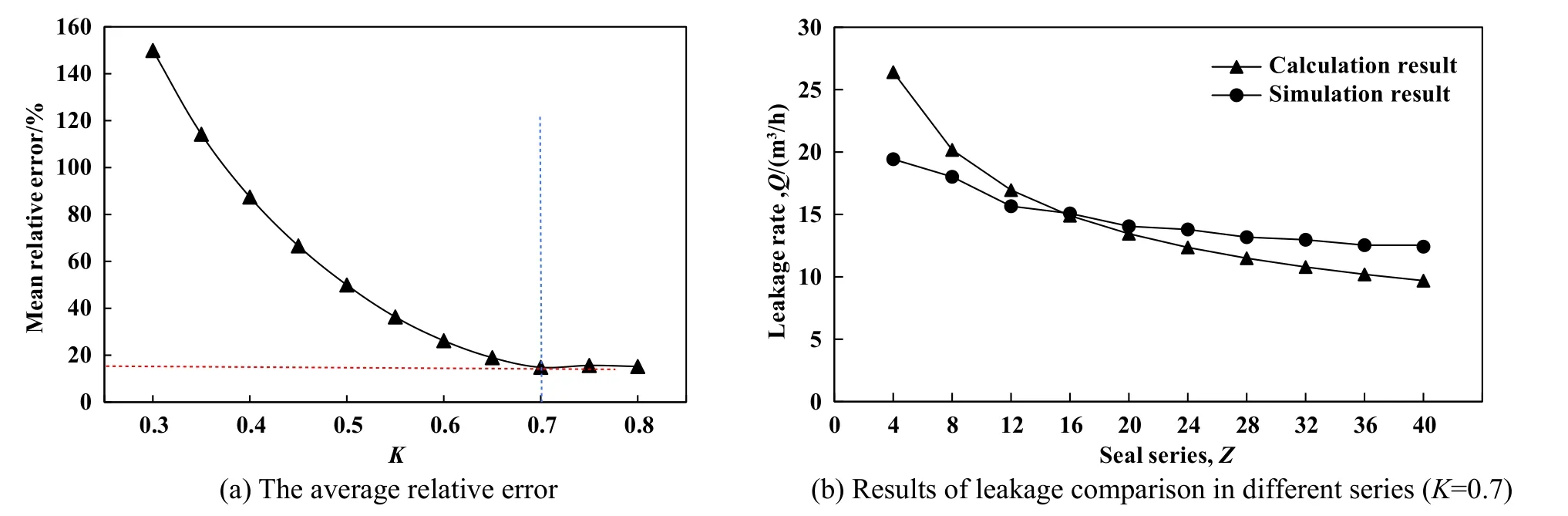
Fig.9 Comparison results of average relative error and leakage in different series (h=150 μm; N=20000 r/min; Pin=0.5 MPa)图9 不同级数下平均相对误差及泄漏量对比结果(h=150 μm; N=20000 r/min; Pin=0.5 MPa)

4.3 基于热力学效应的封严机理研究

4.3.1 压力对密封热力学效应的影响

图10所示为压力变化对熵焓变化的影响规律，可以看出，二者都随压力的增大而增大，呈线性关系.熵增(Δs)随压力的增大而迅速增大，说明压力的升高进一步提升了密封介质动能转化成热能的效率，热能的增加也就越大；焓增(Δh)主要反应密封间隙内温度的变化情况，随着压力的增大焓增呈增加趋势，说明密封介质的温度也随压力增大呈上升趋势.可见，压力的增大对自冲击密封的热力学效应影响显著，因此，如何在高压下实现高效封严将是新型密封的研究重点和方向.

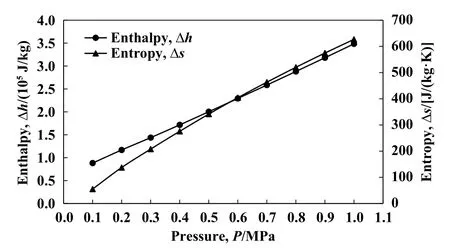
Fig.10 The influence law of pressure change on thermodynamic effect (Z=15; h=150 μm; N=20000 r/min)图10 压力变化对热力学效应的影响规律(Z=15;h=150 μm; N=20000 r/min)

4.3.2 密封间距对密封热力学效应的影响

新型密封的抑漏形式类似迷宫密封，流体的减压降速过程都发生于密封各级的微尺度间隙中，密封间距的变化会直接影响微尺度流场中的能量耗散.图11所示为不同密封间距时的熵焓变化规律，可见，密封间距对熵焓变化有显著影响，二者变化规律基本一致，都随间距的增大而增大，且在密封间距h大于270 μm时，焓增和熵增随间距增大而增大的趋势明显放缓.对于熵值而言，密封间距的增大，增大了内部流体自冲击的能量，使得内能转化量增大，整体熵值增加；对于焓值而言，密封间距的增大同样使得每次冲击时的流体内能转化量增大.但需要说明的是，密封间距的增大仅表明流道内冲击的流体量更多、冲击能量更大、内能转化更多，不代表内能的转化效率越高，内能转化效率还受压力、流速和介质属性等多因素影响，是新型密封需要系统研究的重要方向.

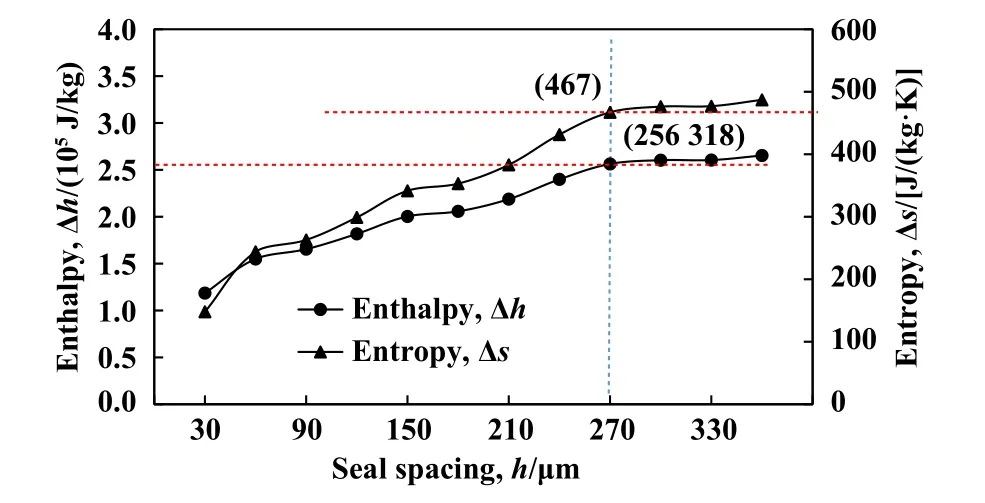
Fig.11 The influence law of seal spacing change on thermodynamic effect (Z=12; N=20000 r/min; Pin=0.5 MPa)图11 密封间距变化对热力学效应的影响规律(Z=12;N=20000 r/min; Pin=0.5 MPa)

4.3.3 泄漏特性综合分析

为系统研究新型密封的泄漏特性，同时验证理论公式，进一步综合分析了压力、密封间距和转速对泄漏量的影响，结果如图12所示.可以看出，不同转速和压力下仿真计算结果与泄漏公式符合最好(不同转速下的结果误差约为7.59%)，不同密封间距下二者的计算结果误差较大，可能大间距下单纯的理论公式未有考虑诸如系数非线性变化、气体流态和涡旋流场等情况，使得与仿真模拟结果出现较大偏差.由图12还可以看出，新型密封泄漏量受压力和密封间距变化影响较大，随压力和密封间距的增大近似呈线性增大趋势.而转速在整个变化区间内对泄漏量的影响较小，表明新型密封的封严特性基本不受转速变化的制约，这一特性使得其被用于各类启停工况频繁及转速变化较大的场合有显著优势.

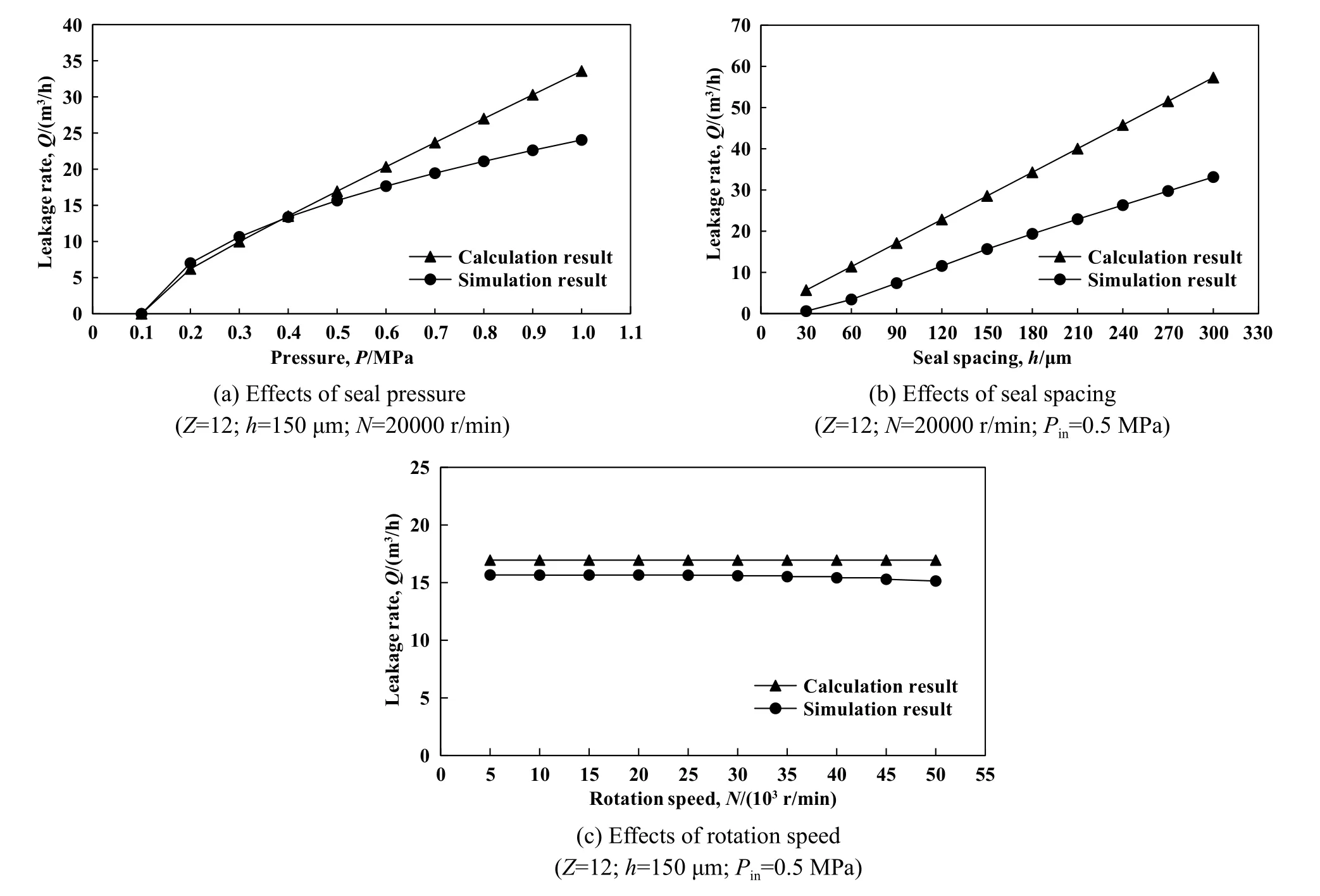
Fig.12 The influence law of various parameters on the leakage characteristics图12 各类参数对泄漏特性的影响规律

4.3.4 温度特性综合分析

根据前文中的分析，新型密封主要是通过影响密封介质的热力学效应来实现封严抑漏的，最终将介质的动能转换为热能，可见，温度的变化及演化特性对新型密封的功能实现至关重要.图13所示为密封级数Z=12时，从密封入口(Z=1)至密封出口(Z=12)位置时各级数对应的温度变化情况，可以看出，由入口开始温度是逐级升高的，至8~10级(第3列位置)温度达到最高(428 K)，与上述温度场表现一致.在图13中所示工况下，以出入口温度为依据，经计算，出口温度(409 K)相对于入口温度(318 K)提高了28.6%，可见，降压手段、散热问题及材质的耐热性将是新型密封结构实用化面临的关键问题.

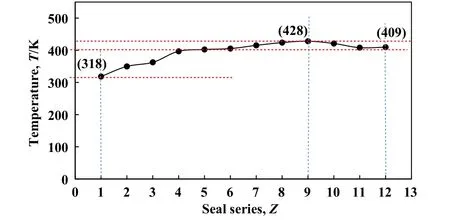
Fig.13 Temperature change from inlet to outlet levels(Z=12; h=150 μm; N=20000 r/min; P=0.5 MPa)图13 入口至出口各级数温度变化(Z=12; h=150 μm;N=20000 r/min; P=0.5 MPa)

图14(a)、(b)、(c)和(d)分别为压力、转速、密封级数和间距变化对自冲击密封出口温度的影响规律，可以看出，出口温度随压力增大呈显著上升趋势，压力仍然是影响密封出口温度的关键因素；转速变化对出口温度的影响仍不明显，一定工况下，超过某一转速时[图14(b)所示为N=30000 r/min左右]后出口温度随转速的升高呈现较缓慢的上升趋势，这是由于较高转速下，气体间的剪切摩擦热以及气体与旋转部件间的摩擦热逐渐增大；出口温度随密封间距的增大呈现逐渐增大的趋势，在密封间距h=270 μm时出口温度最高，说明这一工况下此间距时的动能转化能量最高(能量最高并不意味节流效率最高，节流效率与转化率有关)；出口温度受密封级数的影响较为明显，随级数的增大呈现先降低后平缓的变化趋势，当级数大于20时出口温度变化不再明显，这是由于随着级数的增大，流体于密封通道内的耗散过程也增加，热能分布也越均匀，但级数过大会提高设计和加工难度，应结合实际泄漏要求合理确定密封级数.

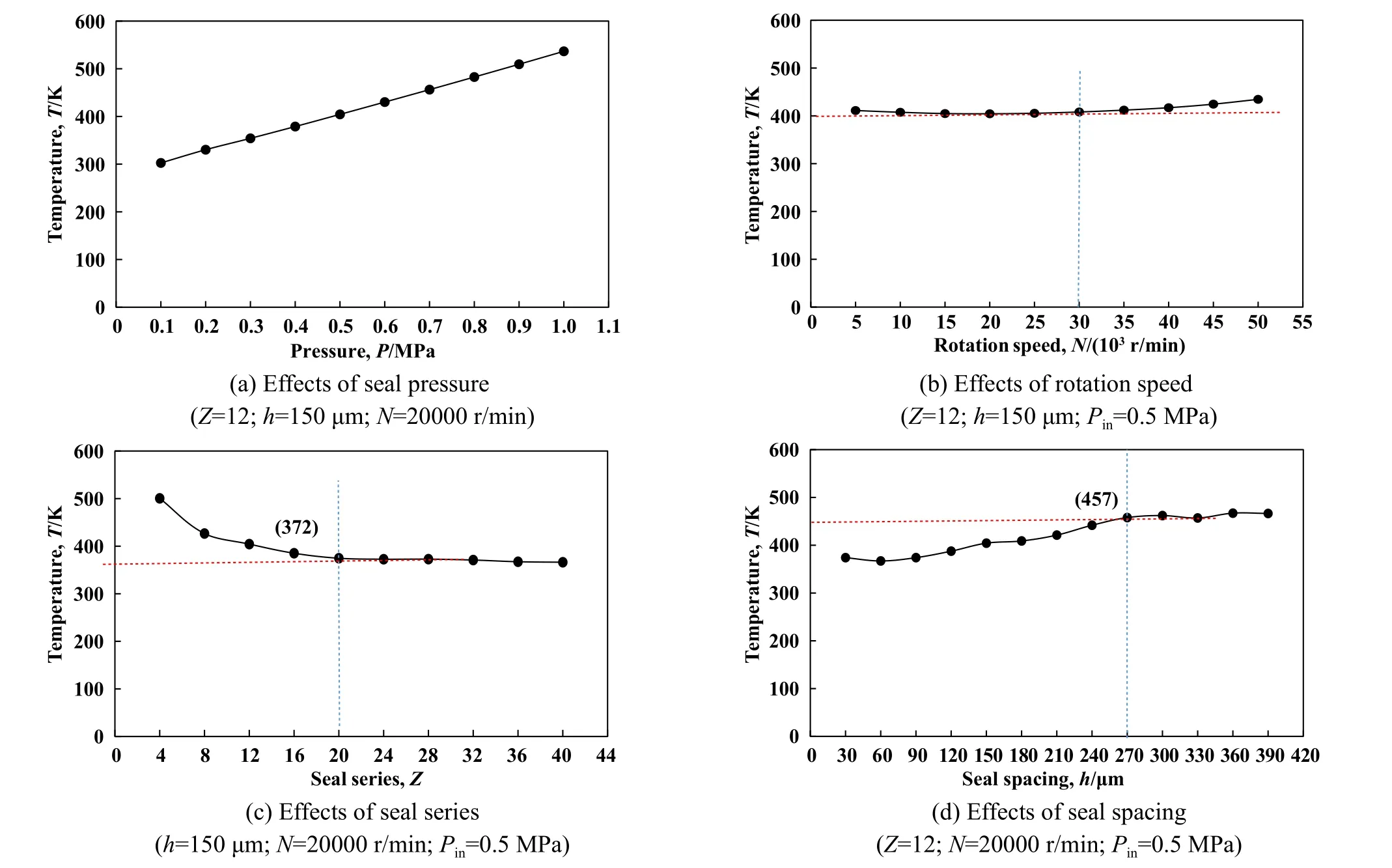
Fig.14 The influence law of various parameters on the temperature characteristics图14 各类参数对温度特性的影响规律

4.3.5 自冲击密封封严机理分析

根据上述研究结果可知，气体通过自冲击密封三维通道时的冲击效应主要包括热力学效应、流束收缩效应和摩阻效应3个效应：

(1) 热力学效应.通过速度云图和温度云图可知，气体通过自冲击密封三维特斯拉阀流道时，由于流道结构的特殊性，密封腔内流体分成两部分并最终在每个密封级交汇区内形成相互冲击，通过逐级不断地冲击致使气体的动能逐步转化为热能而耗散，进而使得温度升高，熵值增加.流体间的冲撞、分叉形成的冲击阻塞效应在交汇位置表现最为强烈，这一位置也是压力能(动能)转化为热能的关键位置，同时气流经过交汇位置时冲击异常剧烈，流体流速经冲击耗能后整体呈降低趋势，动能转化为热能而耗散，流体间的相互冲击作用产生的热力学效应是自冲击密封封严的主要原因.

(2) 流束收缩效应.气体通过自冲击密封交汇区时，由于压差和冲击的作用而产生挤压收缩，被挤压收缩后的气体最终流向下一密封级再次经历相同的冲击收缩过程.收缩效应会使这一短暂阶段内的气体流速升高，温度和压力降低，内能向动能转化，具有瞬时、局部作用的特点.整体而言，流束收缩效应不利于整个密封的抑漏实现，但流速的增大有助于提高下一阶段的冲击阻塞效果.

(3) 摩阻效应.通过温度云图可以看出，高转速下气体与转子的摩擦导致温度沿介质厚度方向逐次变化，气流越接近转子流道壁面，温度越高；气体在通过自冲击密封管道时也会与静止壁面(外环和对应悬柱)产生摩擦，最终也会形成一定的摩阻效应，有利于流道中流体动能向内能转化.可见，摩阻效应能够使气体流速减慢，具有一定的阻流、抑漏效果，有利于自冲击密封封严.

5 结 论

随着现代设计和分析技术的迅速发展，对传统基础类部件(如齿轮、轴承和密封件等)进行结构改进和优化的空间正逐渐消失，新型结构的成功提出则更加困难.自冲击密封是作者所在课题组首次提出的1种新型密封结构形式，目前已初步完成理论分析和机理探索，正在向实用化阶段迈进，这一结构自提出以来得到了广大同行和前辈的高度关注，本文中进一步探究了该结构的封严机理，具体结论包括以下几个方面：

a.提出的考虑热力学效应的密封泄漏量公式，仿真模拟结果与理论公式计算结果符合较好，可以直观地反映出热力学效应与泄漏量之间的关系.

b.热力学效应是自冲击密封封严的主要原因，而流束收缩效应和摩阻效应一定程度上也有利于动能向内能的转化，与现有非接触密封(间隙、螺旋、迷宫及间隙密封等)相比，经自冲击作用后的流体透气效应基本可以忽略，研究如何进一步提高热力学效应是提升自冲击密封封严性能的关键.

c.压力和密封间距增大都会降低自冲击密封内部的热力学效应，增大密封泄漏量，如能在大间距下实现抑漏则会使系统的稳定性更好.所以研究如何提升高压及大间距下新型密封的封严效率是自冲击密封实用化的关键，可进一步结合降压结构设计、耐高温材料选择等思路深入探究.