基于流体动压原理的密封槽型优化方法

何 猛, 刘志远, 李双喜, 毕恩哲, 张江腾, 刘鑫宇

(北京化工大学 机电工程学院，北京 100029)

随着航空航天技术的蓬勃发展，航空发动机封严技术朝着高温、高速及高压差等高参工况进一步发展[1-2]，动压密封作为1种可重复使用的新型高速密封，工作时密封面处于流体动压润滑，磨损小且寿命长，已作为先进密封技术用于压缩机和汽轮机等高端装备[3]，可以很好地适应航空发动机的封严要求[4-5].端面槽型是决定动压密封流体润滑特性的核心因素[6-7]，对其进行优化，能进一步改善其流体润滑性能，减少端面摩擦磨损，提高航空发动机的工作性能.

考虑到实际加工，目前对动压密封槽型的优化主要集中于等深槽优化，包括无定形拓扑优化和定形参数优化.无定形拓扑优化是1种通过确定目标函数，并在约束域中找到最佳的流场分布方案的优化方法，孟祥凯等[8]和Ochiai等[9]对于动压密封拓扑优化的相关工作已经取得了一些进展，然而优化所得槽型并未取得与螺旋槽动压密封性能相当的工程表现，同时，拓扑优化通过边界形状的演变来改变初始设计的几何形状通常需要大量迭代，且很大程度上依赖复杂的正则化技术[10-11].对数螺旋线因其良好的动力特性，广泛应用于动压密封[12-13]，表现出极其优异的流体润滑性能.同时，大量的理论及试验研究均表明，对于特定的优化目标，对数螺旋槽动压密封参数总有1个具体的优化方向[14].相比于无定形拓扑优化下，定形参数优化作为1种通过修改形状参数，实现目标几何形状迭代的方法，计算量相对较小，迭代相对简单，可以很好地用于螺旋槽动压密封的槽型优化.自Etsion等[15]的早期工作以来，参数优化已广泛应用于螺旋槽动压密封，江锦波等[16]和 Hashimoto等[17]分别利用推导广义对数螺旋线极坐标方程和样条函数，李欢等[18]和李双喜等[19]等使用多因素正交分析方法，丁雪兴等[20]和宋鹏云等[21]分别基于刚漏比和开漏比对槽型参数进行了参数优化.

大多数学者忽略了各槽型参数之间的交互影响，同时研究工作是在恒膜厚条件下进行的.实际上，各槽型参数之间的影响不可忽略，基于恒闭合力的优化更能直接反映密封端面的流体润滑状态.本文中基于恒闭合力，兼顾开启力和泄漏率，考虑了各槽型参数间的交互影响，以期进一步提高对数螺旋槽动压密封的流体润滑性能.

1 动压密封工作原理及分析理论基础

1.1 动压密封结构及原理

图1所示为动压密封典型结构，其主要由动环、静环、防转销、辅助密封圈、弹性元件和静环座等组成.

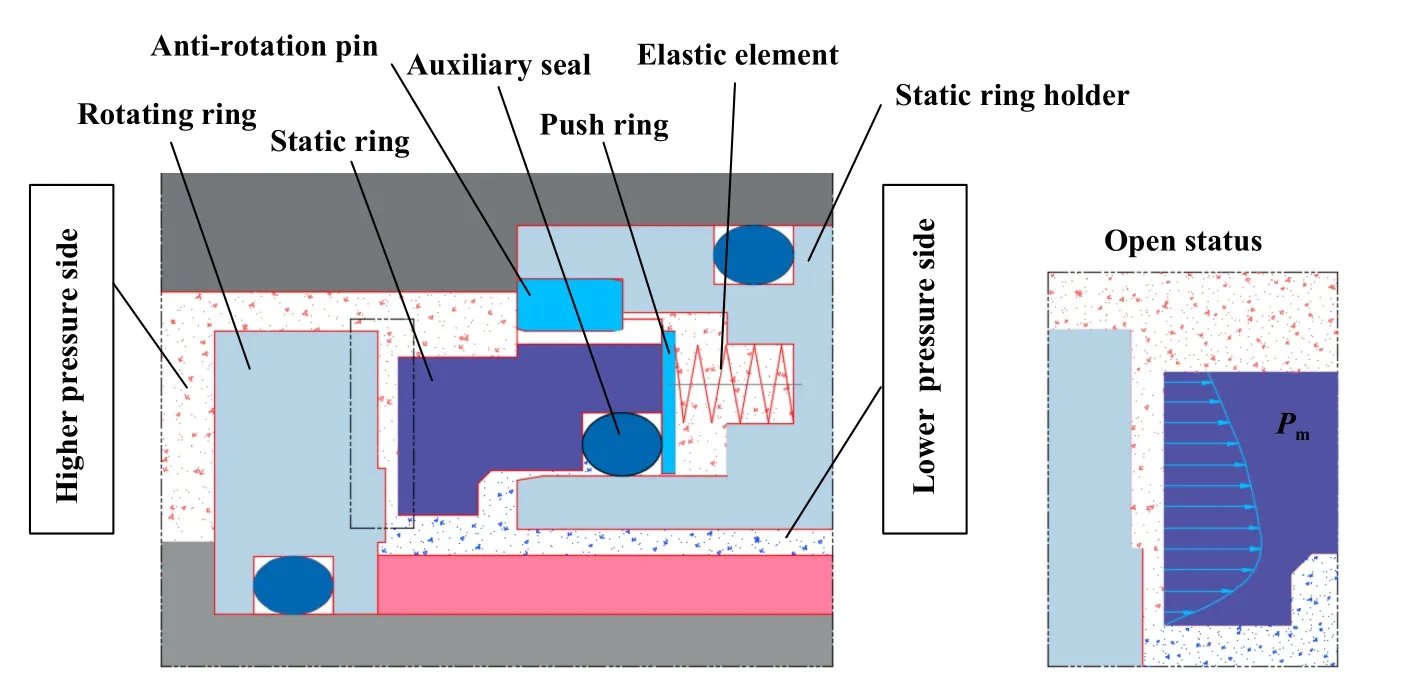
Fig.1 Typical structure and principle of dynamic pressure seal图1 动压密封典型结构及原理

动环表面加工有周期性微槽，当动环旋转时，高压介质从密封面高压侧受迫进入螺旋槽，同时，随着流入方向流道逐渐变窄，速度能逐渐转化为压力能，介质压力在槽根径处达到最大.当动环转速到达一定值后，介质将静环推离，动、静环端面分离，端面间形成一定厚度的正刚度流体膜，同时流体膜在弹性元件和介质压力的共同作用下保持相对稳定，最终实现动压密封非接触长寿命运转.

图2所示为动压密封端面微槽示意图，其位于XY平面，且旋转中心与XY坐标系原点重合，微槽将端面分为槽区和坝区.当动环角速度为ω(rad/s)时，在动环的剪切作用下，流体膜上任意一点(x,y)在X和Y方向上的转速分量可分别表示为

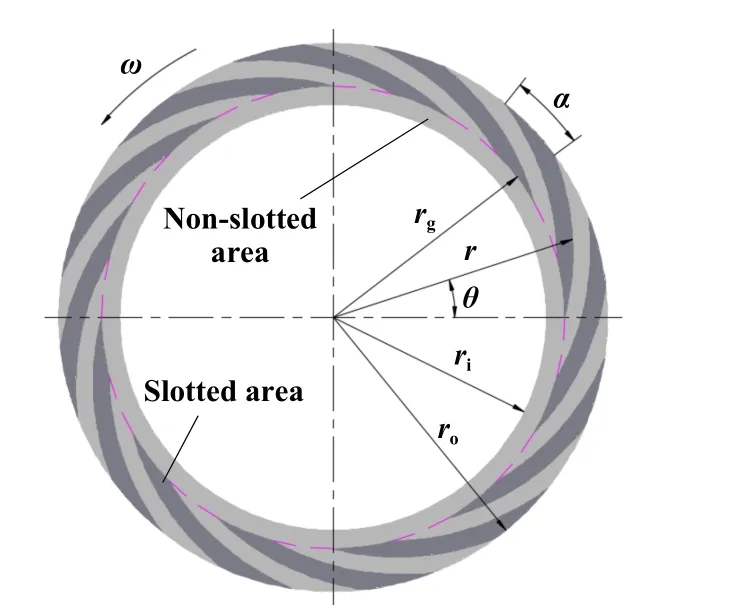
Fig.2 Spiral groove of rotating ring end face图2 动环端面螺旋槽

动、静环密封面开启后，端面流场各区域膜厚h表示为

式中，hm为端面间隙，单位为m；hc为端面槽深，单位为m； ε为区域系数，槽区ε = 1，坝区ε=0.

1.2 动压密封流动模型

由于动压密封端面所加工微槽以及其稳定运转时的流体膜厚度均为微米级，流场可使用薄膜流动进行描述.等温薄膜流动的雷诺方程描述如下[22]：

式中，p为流体膜的膜压，单位为Pa；ρ为介质的密度，单位为kg/m3；μ为介质动力黏度，单位为Pa∙s；u为流体速度，单位为m/s.

介质可视为理想气体时，其密度ρ与压力和温度有关，可表示为

式中，M为气体摩尔质量，单位为mol/kg；R为理想气体常数；T为介质温度，单位为K.

介质动力黏度与温度的关系可以用Sutherland公式表示：

式中，T0为273.15 K；μ0为在标准大气压，273.15 K时的介质动力黏度，当介质为空气时为1.711×10-5Pa·s；S为萨瑟兰数，当介质为空气时为111 K.

1.3 恒闭合力膜厚计算

动压密封的工况稳定时，理想状态下流体介质和弹性元件所形成的密封端面闭合力和密封间隙是恒定的，流体膜对密封面的开启力始终等于密封端面闭合力.因此，恒闭合力计算得到的流场特性反映的是动压密封稳定运转时的状态，本优化即为对其实际运转状态的优化.使用三角形网格对流体膜进行网格划分，如图3所示，将其外侧边界设置为高压入口，内侧边界设置为低压出口，并进行了网格无关性验证，网格数量为15 000~20 000.

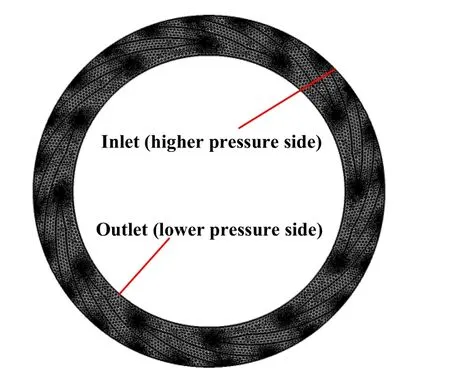
Fig.3 Grid and boundary conditions of fluid film图3 流体膜网格及边界条件

图4所示为动压密封恒闭合力流场特性计算流程，具体流程为给定工况参数下，对于给定槽型参数的动压密封端面，设定初始端面间隙hm0，计算其流体膜开启力，使用密封面恒闭合力F0对其进行判定，以确认端面间隙hm的迭代方向.以此循环，经过多次迭代，最终计算出恒闭合力对应膜厚，输出流体膜流场特性.同时，为保证计算精度，开启力误差Δ设为1 N，端面间隙迭代步长Δhm设为0.01 μm.

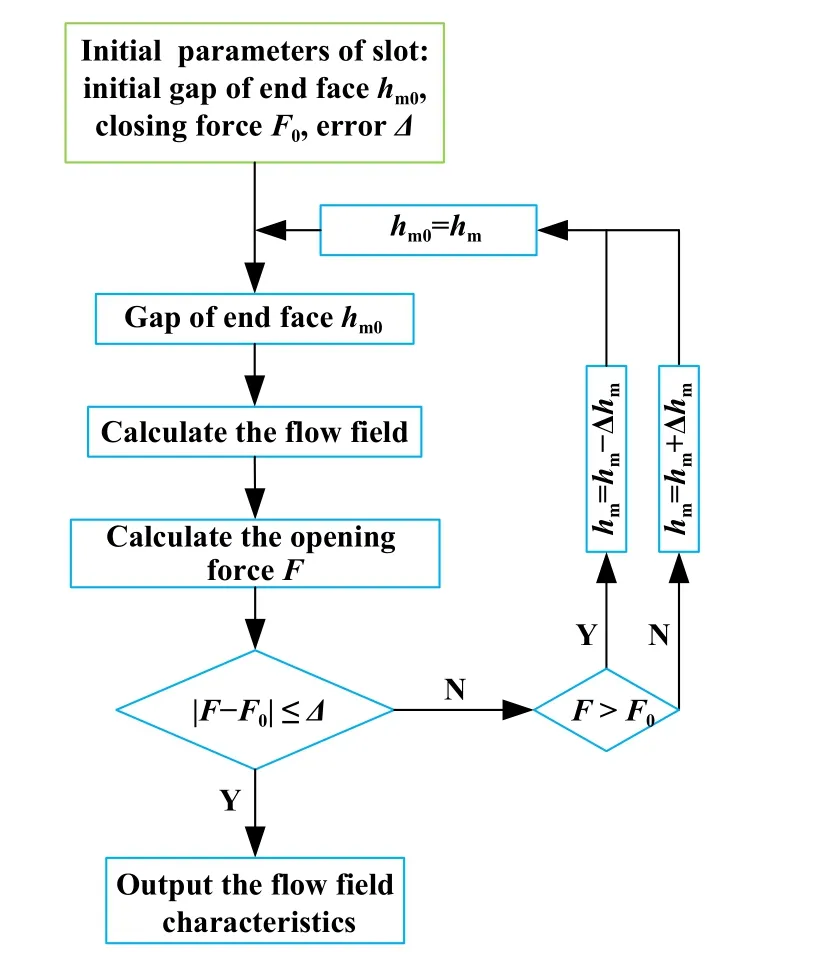
Fig.4 Constant closure force flow field calculation process图4 恒闭合力流场计算流程

1.4 结构及工况参数

典型对数螺旋槽参数示意如图2所示，其结构参 数列于表1中.

表1 典型螺旋槽参数Table 1 Typical spiral groove parameters

各参数之间的关系为

式中，r为螺旋线极径，单位为m；γ1为槽宽比；γ2为槽坝比；θ为极角，α为螺旋槽的周向角度，单位均为rad.

动压密封的工况及设计参数列于表2中.

表2 密封工况及设计参数Table 2 Working conditions and design parameters of seal

2 基于恒闭合力的优化方法和优化模型

2.1 基于恒闭合力的优化方法

二次近似约束优化(BOBYQA)[23-24]是1种主要针对复杂函数且不需计算目标函数导数的优化算法，该算法通过在插值区间内用二次近似函数替代目标函数进行迭代求解，解决多维非线性优化问题，采用的算法基本流程如下：

对于目标变量空间内最小值问题的求解问题，确定最小目标函数.

式中，f为目标函数；Rn为自变量及其区间组成的n维变量空间.

1) 迭代步数k=0时，给定初始向量x0、初始可信赖域半径ε及结束可信赖域半径φ，其中，ε≥φ>0；

2) 构建初始区间的插值函数集{xj|j=0,1,2,3···,m}，m为区间[n+2, (n+1)(n+1)/2]的1个整数.

式中，ei为多维变量空间第i个向量值，例如对于3变量的函数f(x)，其变量空间维数n为3，对于其变量空间中的初始值x0=(1, 2, 3)，e1为(1, 0, 0)，e2为(0, 2, 0)，e3为(0, 0, 3)；ai和bi分别为ei区间的左右端点值.

3) 开始进行迭代运算，并记为k=k+1.

4) 第k次迭代时，若满足收敛条件，优化完成，否则，开始进行步骤5操作.

5) 找出插值函数集中存在的最小值点xk.

6) 通过求解可信赖域的子问题确定试探步长dk.

7) 取信任区域半径Δk，构造新的差值点xk+1.

8)构建新的二次近似公式及下一步迭代的信任区域半径，直到找到变量空间最小值.

2.2 优化数学物理模型

基于端面恒闭合力(F0=710 N)，对表1中典型螺旋槽流体膜参数进行流场建模、网格划分，按表2中工况参数将流体膜高压侧设为压力入口，低压侧设为压力出口，将流体域X、Y向速度按式(1)设置，并进行网格无关性验证，以确保模型的准确性.按图4流程迭代计算，得到不同转速下典型螺旋槽动压密封特性参数列于表3中.

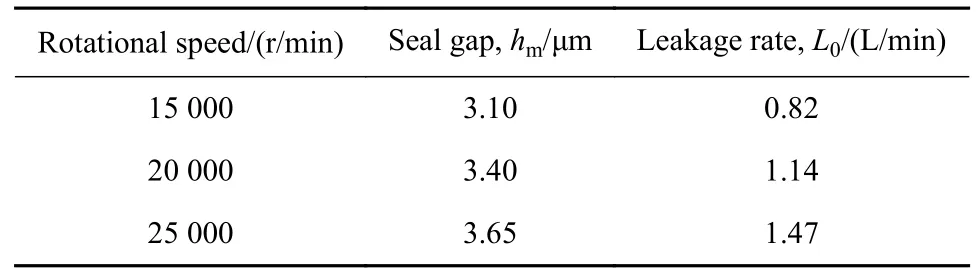
表3 典型参数螺旋槽动压密封恒闭合力特性Table 3 Constant closure force characteristics of typical parameters of spiral groove dynamic pressure seal

2.2.1 目标函数及约束

为提高密封润滑性能，要求密封在各转速膜厚下，不降低开启力的同时，尽可能降低泄漏率.优化目标函数及约束条件分别表示为

式中，L为流体膜泄漏量，单位为L/min；Ω为流体膜积分域；F为流体膜开启力，单位为N；A为流体膜积分域，单位为m2；l为流体膜半径为r的圆周路径.

由 式(3)， 令 ϕ(p,h, µ, ρ,u) =应用增广拉格朗日方法引入式(15)的约束条件，将优化问题转化为无约束优化问题，增广拉格朗日函数表示为

式中，a1、a2和a3为拉格朗日乘子；b1和b2为惩罚函数，用来确保精确的开启力和泄漏率约束，以及数值稳定.

2.2.2 初始值及变量区间

由于β、γ1和γ2在目标函数空间内处处连续，可直接作为目标函数的自变量，而槽数N为整数，在目标函数空间不连续，将其直接表示为目标函数的自变量是不恰当的，因此将其作为独立变量.螺旋槽槽型参数初始值x0及变量区间分别为

按表3设置对应转速下的膜厚及约束条件，各参数迭代步长比例因子均取为1，约束容差设为1×10-2，优化容差设为1×10-5，最大迭代步数设为1 000，进行不同转速各槽数下的迭代计算.

3 优化结果及机理分析

3.1 优化槽型流场特性及结构参数

3.1.1 泄漏率和开启力分布

经迭代计算，得到转速分别为15 000、20 000和25 000 r/min时，随独立变量槽数N变化的流体膜润滑特性参数及结构参数分布.

图5所示为不同优化转速下优化槽型泄漏率和开启力随槽数N的分布.显然，优化所得槽型的泄漏率和开启力满足约束条件，本文中提出的优化方法是可行的.不同转速下，随着槽数的增加，优化槽型的泄漏率明显低于优化前典型参数螺旋槽各转速泄漏量，平均降低9%以上，开启力基本变化较小，低于1%.这说明相对于开启力，泄漏率为目标函数的主要贡献，同时泄漏率和开启力的相对稳定说明转速和槽数对目标函数的值影响较小.

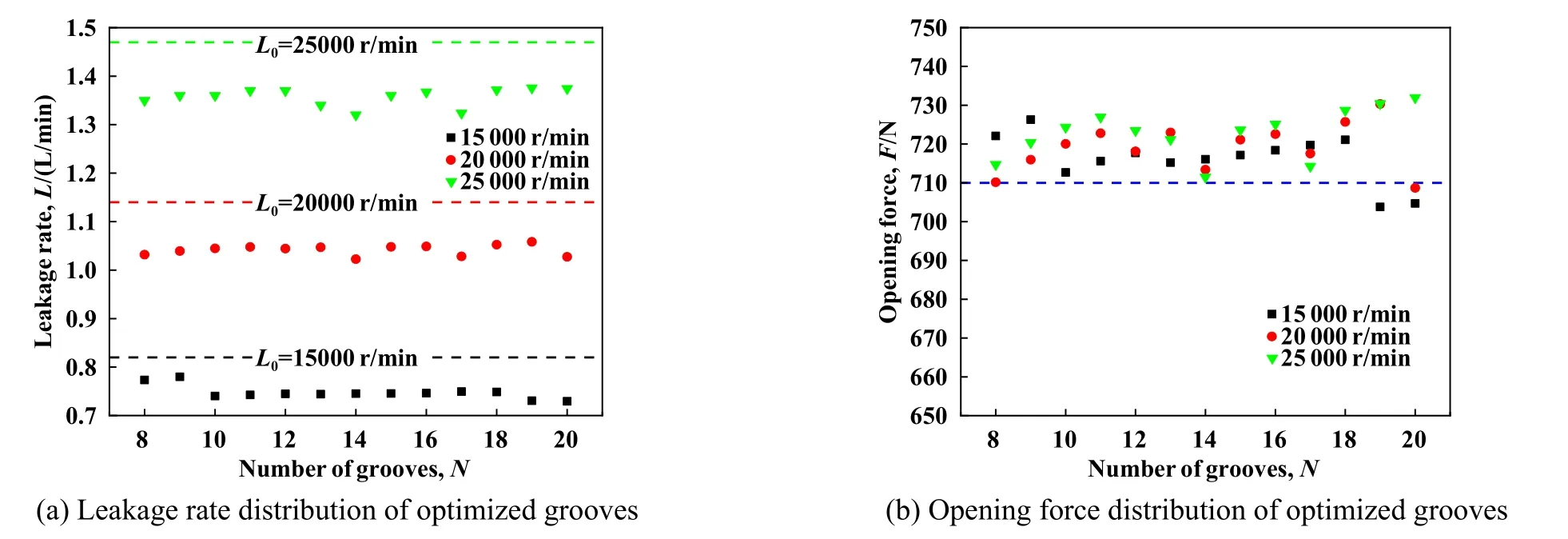
Fig.5 Leakage rate and Opening force distributions of optimized grooves图5 优化槽型泄漏率和开启力分布

3.1.2 结构参数分布

图6所示为不同槽数下，优化槽型结构参数螺旋角β，槽宽比γ1和槽坝比γ2随槽数N的分布.随着槽数的增加，不同转速下，各结构参数存较大变化，但大部分参数分布较为集中，以槽数N=12为界，优化槽型整体上表现为2种槽型，1种螺旋角为22.5°，槽宽比为0.5，槽坝比为0.55，将其命名为A槽型，第2种螺旋角为17.5°，槽宽比为0.55，槽坝比为0.55，将其命名为B槽型.这说明，在槽数N大于或小于12时，获得的优化槽型结构参数基本不受优化转速和槽数的影响，本文中提出的优化方法具有较好的适用性.

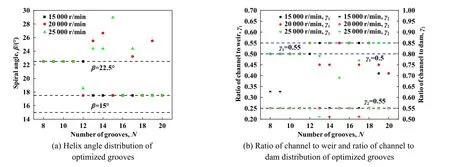
Fig.6 Parameters distribution of optimized grooves图6 优化槽型参数结构分布

3.2 优化槽型流场特性

为了方便分析对比，选取槽数N为12时的A、B槽型，与典型螺旋槽进行对比分析，进一步分析优化槽型流场特性.转速为15 000 r/min，密封间隙hm为3.10 μm时3种槽型的流场特性参数列于表4中.相较于优化前，A、B槽型流体膜开启力基本保持不变，泄漏率均减少9%以上.

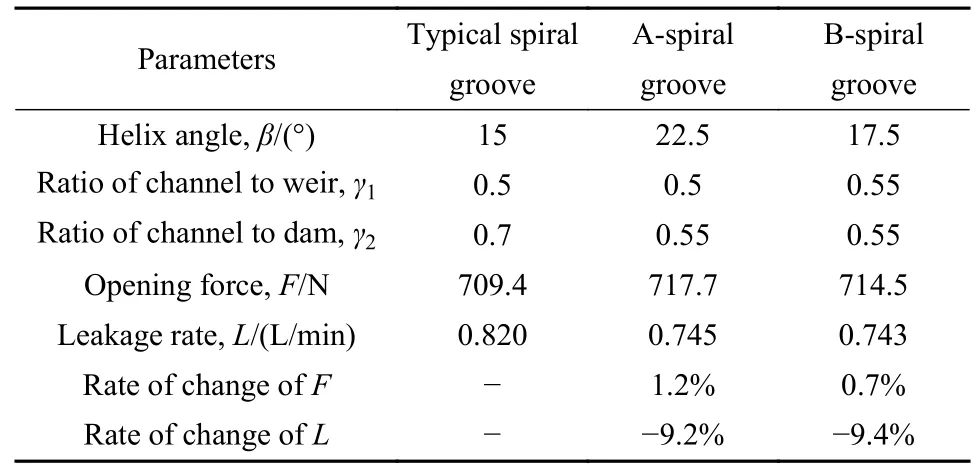
表4 3种螺旋槽型特性参数Table 4 Characteristic parameters of the three types of spiral grooves

图7所示分别为3种槽型的压力分布云图.相比于典型螺旋槽，A、B两种优化槽型高压区(红色区域)面积显著增大，产生了更明显优化型的动压效应，压力峰值分别增加了15.2%和12.8%.

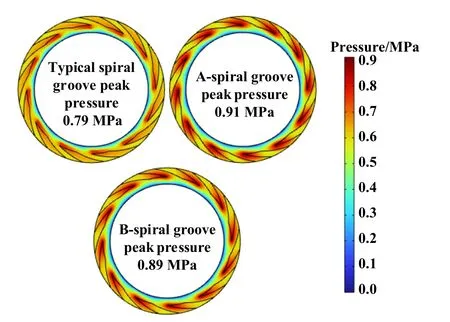
Fig.7 Pressure distribution of three types of spiral groove图7 3种螺旋槽型压力分布

进一步地，对3种槽型流场进行分析，图8所示为提取各槽型流体膜状态的槽、坝区监测曲线，监测曲线分别位于各槽型的槽区和坝区正中位置.

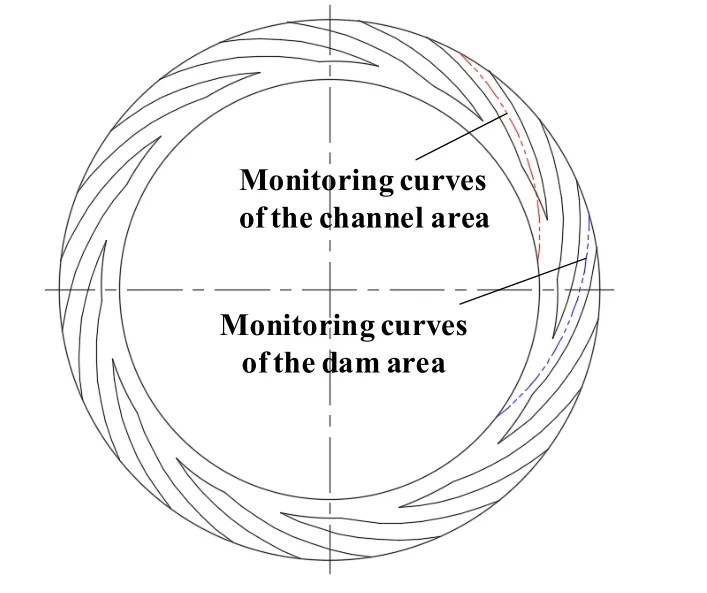
Fig.8 Monitoring curves in the channel and dam areas图8 槽、坝区监测曲线

3.2.1 压力分布

图9所示为3种槽型沿槽坝区中线提取到的压力及速度分布曲线.由图9(a)中各监测曲线压力峰值可知，典型螺旋槽的槽区峰值明显高于坝区，而A、B槽型的槽、坝区压力峰值相当，同时优化所得A、B槽型的压力峰值均高于典型螺旋槽.进一步说明优化槽型的动压效应更强，同时周向压力梯度更小.

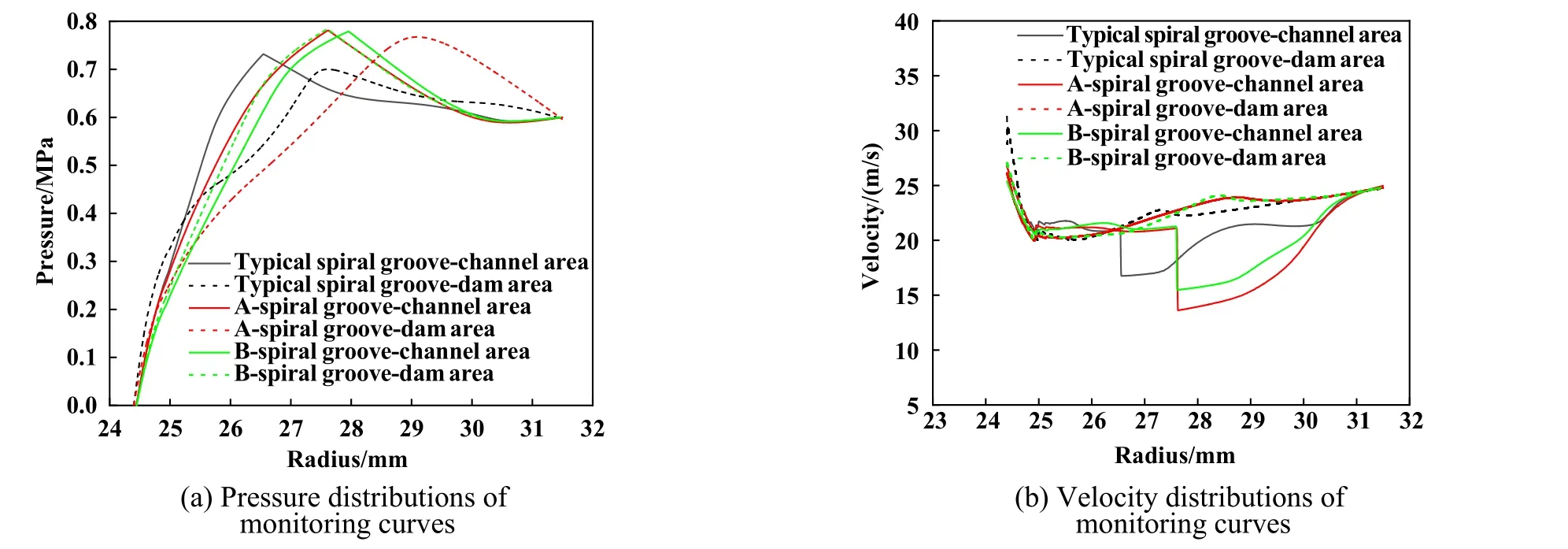
Fig.9 Pressure and velocity distributions of monitoring curves图9 监测曲线压力和速度分布

各槽型的压力参数对比列于表5中，其中峰值位置是指槽、坝区曲线压力峰值相对于流体膜中心的距离.峰距是指槽、坝区压力曲线峰值径向位置差值.第1行为B槽型相对于典型螺旋槽的变化，其变化说明槽坝比和螺旋角能改变流体膜高压区的径向位置，压力峰值径向位置随螺旋角增大和槽坝比减小而外移；第2行为A槽型相对于B槽型的变化，其变化说明螺旋角和槽宽比能改变流体周向压力梯度，周向压力梯度随螺旋角增大和槽宽比减小而减小.这说明相对于典型螺旋槽，A、B槽型通过均化高压区周向压力增强开启力的同时，又通过减小槽坝比改变高压区径向位置减弱开启力，最终保持开启力的基本稳定.

表5 各槽型结构压力对比Table 5 Comparison of pressure of different structures

3.2.2 速度分布

由图9(b)中各速度监测曲线可知，由于流体受迫进入动压槽内后，在槽根径处，速度降至最低，速度能转化为压力能，形成了压力屏障，流体进入密封间隙后，在压力屏障作用下，槽区流体速度在槽根处降至最低，而坝区流体速度在到达槽根径前始终较为平缓，槽区流体越过槽根径后与坝区流体汇合，进入剪切力、离心力和压差相对平衡的稳流区，随着进一步流入，离心力减弱，在流体膜压差的主导下，流体迅速流出密封间隙.

各槽型流体从高压侧进入密封间隙时，速度相同，而在流出密封间隙时，典型螺旋槽的坝区流出速度远高于槽区，流体在流动过程中发生了从槽区向坝区的转移，而优化槽型的槽、坝区流出速度与典型螺旋槽槽区相当.这说明，相对于典型螺旋槽，优化槽型压力峰值外移，压力峰值处的速度减小，同时内侧压力梯度减小，流体滞留长度变大，流体出口流速降低，最终实现泄漏率的降低.

因此，槽型优化过程的机制为通过调整螺旋角、槽宽比和槽坝比，外移压力峰值，增强动压效应的同时降低流体膜平均压力，实现流体膜开启力基本不变，同时压力峰值外移，内侧压力梯度降低，滞留长度变大，降低流体膜泄漏率.

3.3 流体润滑性能对比

对动压密封来说，在实际运转工况下，一定的流体膜厚度和足够的流体膜刚度是保证密封非接触和自适应运转的前提.流体膜厚度不够或者流体膜刚度不够强甚至是负刚度时，容易发生密封端面的碰磨.因此，需要对优化所得槽型的流体润滑性能进行分析.

3.3.1 流体膜开启力

基于恒闭合力(F0=710 N)，计算得到3种槽型的流体膜开启膜厚和刚度特性曲线，如图10所示.由膜厚曲线可知，随着转速的增加，各槽型流体膜厚度逐渐增加，且趋于平缓，3条曲线在11 000 r/min左右处相交.由于曲线基于恒闭合力，同转速下曲线膜厚越小，对应槽型开启力越弱，因此，在转速小于11 000 r/min时，各槽型流体膜开启力表现为典型螺旋槽>B槽型>A槽型，在转速高于11 000 r/min时，各槽型流体膜开启力表现为A槽型>B槽型>典型螺旋槽.

Fig.10 Film thickness curves in opening state图10 开启膜厚曲线

3.3.2 流体膜生成率

流体膜生成率定义为开启膜厚曲线斜率，其大小为每单位转速增加的流体膜膜厚.由图10流体膜生成率曲线可知，随着转速的增加，流体膜生成率随着流体膜厚度的增加而减小，3种槽型流体膜生成率逐渐趋于同一稳定值，槽型对流体膜生成率的影响逐渐降低，但始终表现为A槽型>B槽型>典型螺旋槽.

3.3.3 流体膜泄漏率

基于恒闭合力，计算得到如图11所示的3种槽型在不同转速下的流体膜泄漏率特性曲线.由曲线可知，在较大转速范围内，典型螺旋槽的泄漏率最大，B槽型的泄漏率最低，A槽型的泄漏率居中.随着转速的增加，由于开启膜厚的增加，各槽型泄漏率逐渐增加，且增长速度越来越大，A槽型曲线最终超过典型螺旋槽曲线，这意味着超过一定转速，相对于典型螺旋槽，A槽型不再具有泄漏量优势，B型槽仍然存在泄漏量优势.

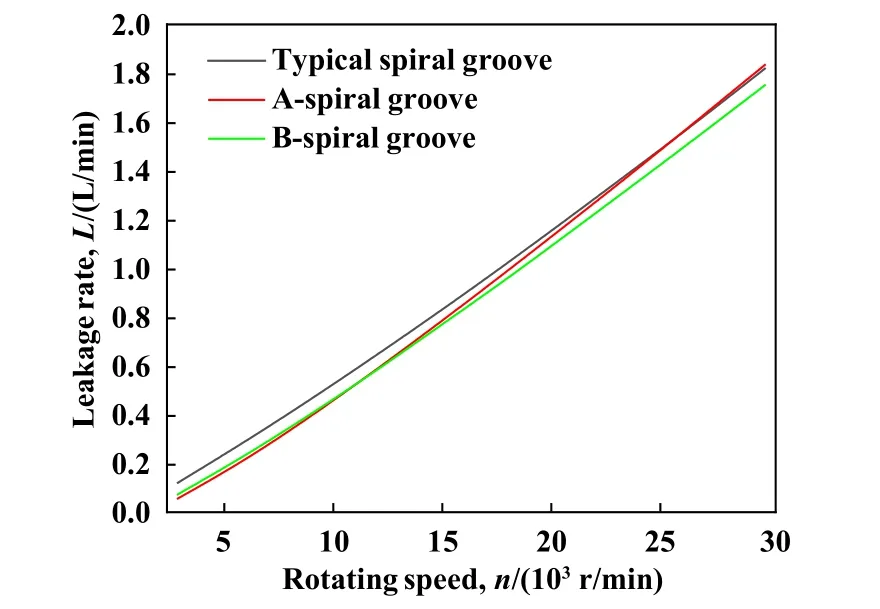
Fig.11 Leakage rate curves in opening state图11 开启泄漏率曲线

如图9所示，根据膜厚大小，以11 000 r/min为界，将转速分为小膜厚段和大膜厚段2个转速阶段.在小膜厚段，流体膜泄漏率虽然较低，但容易因振动而发生碰磨，流体膜的高膜厚为优先考虑因素.而大膜厚段，流体膜厚度足以适应振动工况，流体膜的低泄漏率为优先考虑因素，在小膜厚段，流体膜生成率均较大，因此高膜厚的典型螺旋槽为优选槽型，而在大膜厚段，泄漏率较低的B型槽为优选槽型，而A型槽在全膜厚段的表现介于二者之间.

4 结 论

本文中基于流体润滑原理，以改善端面密封流体润滑性能为目的，基于恒闭合力对端面密封提出了最小化泄漏率与开启力之比的目标函数，进行数学表征并建立了优化模型，总结了优化槽型的参数规律.

a.虽然不能保证优化槽型在全转速段的目标函数实现，但在相当大的转速范围内能够保证目标函数的实现，改善动压密封的流体润滑特性，具有较好的适用性，对于用具体形状参数描述的其他定型的表面织构，可以使用本方法进行不同目标函数下的优化.

b.基于新优化方法的研究虽然考虑了转速和槽数对优化槽型的影响，但尚未探究不同恒闭合力对槽型优化结果的影响，同时各变量的迭代步长可能会影响最终的槽型分布，因此可以在这2个方面着手做一些更细致的研究.

c.与优化槽型相比，典型参数螺旋槽动压密封流体润滑性能表现依然优异，其槽型参数具有良好的适用性，这是典型参数螺旋槽动压密封广泛应用的原因.在动压密封槽型实际设计工作中，可以将典型螺旋槽参数作为1个良好的初始设计，再给定目标函数再对其进一步优化，以满足工程需要.