多斜孔节流气浮支承的微振动特性研究

李世泽, 于普良*, 鲁 炅, 尹先雄, 徐 珲, 胡 回, 罗 强

(1.武汉科技大学 冶金装备及控制教育部重点实验室, 湖北 武汉 430081;2.武汉科技大学 机械传动与制造工程湖北省重点实验室, 湖北 武汉 430081;3.武汉科技大学 精密制造研究院, 湖北 武汉 430081)

气浮支承因其高精度、零污染等特性被广泛应用于高精密加工机床、光学测量[1-4]等领域.然而相对于传统机械接触式轴承其承载力和刚度较低[5].Li等[6]分析了均压腔参数对小孔节流气浮支承静态承载性能的影响.Belforte等[7]推导了气浮支承压力分布计算公式，并进行了理论计算.Wen等[8]提出了1种网格自适应建模方法，通过仿真计算发现具有均压槽的气浮支承具有更高的承载特性.

虽然均压槽和均压腔等结构可提高气浮支承的刚度及承载力，但均压腔内会产生湍流涡现象，从而导致气浮支承微振动[9].随着超精密加工技术的快速发展，对超精密仪器的要求越来越高，气浮支承的微振动对超精密设备的加工精度的影响已不可忽略[10-11].Chen等[12]发现气浮支承均压腔内存在气旋现象，并提出该现象是造成微振动的主要因素.Aoyama等[13]通过在节流孔出口处加工圆角，使均压腔内的气旋强度降低，从而提升了气浮支承的稳定性.Li等[14]在均压腔内部设计了1种扰流结构，并进行了数值计算和试验研究，结果表明扰流结构可改善节流孔出口附近流场特性从而抑制气浮支承的微振动.Feng等[15]利用3D打印技术制造了4种不同的节流结构，并进行了仿真及试验研究，结果表明4种节流结构的静态承载性能基本保持不变，且带弧形孔的气浮支承稳定性最好.Li等[16]提出了1种带回流通道的气浮支承，并进行了仿真计算及试验研究，结果表明带回流通道的气浮支承比传统小孔节流气浮支承具有更高的承载力、刚度以及更好的稳定性.

本文作者为进一步提高气浮支承的稳定性，基于湍流涡的形成机理，设计了1种新型多斜孔节流气浮支承.采用大涡模拟方法，分析了气浮支承的流场特性，并在此基础上研究了节流孔倾斜角度、节流孔高度、节流孔直径和供气压力对气浮支承微振动特性的影响，为高稳定性气浮支承的设计提供一定的理论参考.

1 多斜孔节流气浮支承的结构设计

小孔节流气浮支承的结构如图1所示，本节中采用大涡模拟方法对其二维流场进行了仿真分析.其结构及仿真参数为均压腔直径dq=3 mm，节流孔直径d=0.3 mm，均压腔高hq=0.1 mm，孔高ha=0.4 mm，气浮支承直径D=30 mm.流体为可压缩的理想气体，供气压力P1=0.4 MPa，出口压力P0=0.1 MPa，气膜厚度hm=15 μm，温度T=273 K.

Fig.1 Schematic diagram of small-hole aerostatic bearing structure.图1 小孔节流气浮支承结构示意图

图2和图3所示分别为气浮支承的瞬态流场流线及压力分布云图和速度云图.由图2及图3可知，气体流出节流孔后，会在均压腔内形成一系列尺度大小、旋转方向不同的湍流涡.在这些湍流涡的周围气体流线会发生弯曲，同时由于湍流涡的存在，均压腔内也会形成多个低压区域.

Fig.2 The nephogram of pressure distribution and streamline of transient flow field of aerostatic bearing图2 气浮支承瞬态流场流线及压力分布云图

Fig.3 Velocity nephogram of aerostatic bearing图3 气浮支承速度云图

为更好地阐述均压腔内湍流涡的形成机理，将气浮支承气体流动状况用图4所示气体流动简图表示.

Fig.4 Schematic diagram of gas flow state in chamber图4 均压腔内气体流动状态示意图

高压气体V1经过节流孔后，流动横截面积突然变大，大部分气体仍保持竖直向下的速度方向，从而与均压腔上表面发生分离，形成分离区A.V1在冲击到气浮支承底部时，空气会压缩并积聚，形成压缩区B.气流V2在分离区A和压缩区B之间形成的通道C中流过.气流V2进入均压腔时，会在分离区上膨胀，使局部气体流速增加.气流在冲击到底面后，流线发生偏转形成气流V3.V3碰撞到均压腔上表面后分离形成V4与V5.这些速度大小、方向不同的气流在均压腔内与周围气体相互作用，形成一系列尺度大小和旋转方向不同的非稳态湍流涡.这些湍流涡随着气体的流动不断产生、发展及消散，使气膜压力发生波动，从而造成气浮支承的微振动.

由以上分析可知，湍流涡的形成与气体流线的偏转及速度的变化有关，而湍流涡的存在会使气膜压力发生波动，并导致气浮支承微振动.基于这一原理，若改变节流孔倾斜角度，可使气体进入均压腔后有水平流动的趋势，气流不再垂直冲击气浮支承底面，气体流动方向的转变将得到缓和，湍流涡的形成将被抑制.因此，本文作者设计了1种新型多斜孔节流气浮支承，如图5所示.多斜孔节流气浮支承工作参数和结构参数列于表1中.

表1 气浮支承结构及工作参数Table 1 Aerostatic bearing structure and working parameters

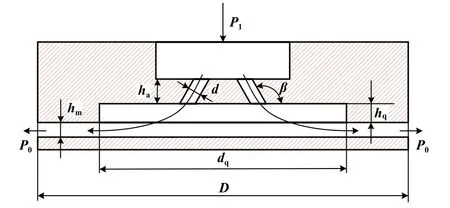
Fig.5 Schematic diagram of aerostatic bearing section图5 气浮支承剖面示意图

2 气浮支承CFD模型及仿真参数设置

2.1 大涡模拟控制方程

气浮支承流场中流体运动满足能量、动量和质量3个守恒定律，包括能量方程、动量方程和连续性方程.其笛卡尔坐标系下的N-S方程为[17-19]

式中， ρ为气体密度；t为时间；ui和uj分别为笛卡尔张量中速度在i方向和j方向的分量；xi和xj分别为i和j方向的坐标； σij为黏性应力张量分量；E为单位质量的流体所具有的内能；qi为笛卡尔坐标系下气体流场i方向的热流密度；P为气体压力.

采用密度加权滤波对式(1~3)进行过滤，得到式(4~6)所示的大涡模拟控制方程.密度和压力由物理空间过滤，用上标“-”表示；采用密度加权滤波过滤温度、速度和内能，用上标“~”表示.

通过大涡模拟，可得到气膜底面的瞬时压力分布，对其积分可得气浮支承的瞬时承载力.

用瞬时承载力的标准差 σ来描述气浮支承的微振动强度，如式9所示.

式中，Fi为第i个时间步的瞬时承载力，为瞬时承载力的平均值，n为总时间步数.

2.2 气浮支承网格划分

由于气浮支承具有对称性，为提升计算效率，取1/4气域模型进行计算，其CFD (Computational Fluid Dynamics)模型如图6所示.为保证网格划分质量和计算精度，采用六面体网格进行划分.为便于阐述，在与对称面夹角为45°的位置取一截面A，如图6(a)所示.图6(b)所示为截面A的网格划分示意图.其中，节流孔径向不少于60个节点，节流孔长度方向不少于100个节点.均压腔的X方向不少于400个节点，在靠近节流孔的位置进行加密.Y方向不少于40个节点，节点采用钟形曲线分布形式(bell curve)，网格越靠近壁面，网格尺寸越小，最小网格尺寸在0.001 mm左右.在气膜厚度方向网格不少于10层，经网格无关性验证后，整体网格数量保持在200万以上.

Fig.6 Schematic diagram of CFD model of aerostatic bearing图6 气浮支承CFD模型示意图

2.3 边界条件及求解参数设置

气浮支承的边界条件设置如图7所示.气体入口设置为压力入口边界条件(pressure-inlet)，供气压力设置为P1=0.5 MPa，气体出口设置为压力出口边界条件(pressure-outlet)，其压力P0等于环境压力.气浮支承气域左右剖面设置为对称边界条件(symmetry)，其余边界均设置为壁面(wall).

Fig.7 Schematic diagram of the boundary conditions of the aerostatic bearing图7 气浮支承边界条件示意图

采用基于压力—速度耦合的PISO (Pressure-Implicit with Splitting of Operators)算法求解本 模型.压力、动量采用二阶迎风格式(Second order upwind)，在保证足够精度的情况下选用非迭代时间步(Non-Iterative Time Advancement)提升计算效率.时间步长的选取应满足CFL (Courant–Friedrichs–Lewy condition)条件[22]，本文中时间步长取 1×10-8s.

3 仿真方法适用性验证

为验证大涡数值模拟模型及计算方法在计算多斜孔节流气浮支承流场时的适用性和有效性，采用Feng等[15]发表的IHB型气浮支承的试验数据，将LES(Large eddy simulation)的计算得到的结果与试验所得到的结果进行对比[23].Feng文献中的气浮支承结构参数分别为节流孔直径d=0.2 mm，节流孔高度ha=0.4 mm，均压腔高度hq=0.2 mm.均压腔直径dq=8 mm，气浮支承直径D=30 mm.

LES计算结果和试验结果如图8所示.由图8可以看到，采用LES计算得到的径向压力分布结果与试验所得到数据基本吻合.验证了大涡数值模拟模型及计算方法的适用性和有效性.

Fig.8 Comparison diagram of simulation results and experimental results[15]图8 仿真与试验结果[15]对比

4 仿真结果分析

4.1 节流孔倾斜角度对微振动的影响

在保证其余参数不变的情况下，计算了当供气压力P1=0.5 MPa，节流孔高度ha=0.4 mm，节流孔直径d=0.2 mm时，节流孔倾斜角度β分别为90°、95°、100°、105°、110°、115°、120°、125°和130°时的气浮支承的微振动特性.

图9所示为节流孔倾斜角度分别为90°、100°、110°、120°和130°气浮支承截面A的压力云图速度流线图和涡量云图.可以看到，当β=90°时，气浮支承节流孔两侧气体流线紊乱，均压腔内存在较多的湍流涡；当节流孔倾斜角度β逐渐增加到110°时，节流孔两侧气体流线紊乱程度降低，均压腔内湍流涡逐渐减少；当节流孔倾斜角度β继续增加到120°时，节流孔左侧气体流线紊乱程度进一步降低，右侧气体流线开始出现波动，均压腔内节流孔左侧的涡量进一步减小，但节流孔右侧的均压腔中会形成大量湍流涡；当节流孔倾斜角度继续增加到130°时，节流孔右侧气体流线更加紊乱，均压腔内节流孔左侧的湍流涡继续减小，节流孔右侧湍流涡会随着气流充满整个均压腔.由以上分析可以看到，随着节流孔倾斜角度逐渐增大，均压腔内的湍流涡先减少再增加，在节流孔倾斜角度为110°时气浮支承涡量较小.

Fig.9 Pressure nephogram and velocity streamline and vorticity nephogram of different orifice inclination angles图9 不同节流孔倾斜角度下气浮支承压力云图、速度流线图和涡量图

图10所示为不同节流孔倾斜角度下气浮支承平均承载力和瞬时承载力的标准差.由图10可以看到，随着节流孔倾斜角度的改变，气浮支承的平均承载力基本不发生变化.瞬时承载力的标准差呈v型，其值随节流孔倾斜角度的增加先减小再增大，在β=110°时其标准差较小，与涡量云图的变化规律一致.

Fig.10 Average loading capacity of aerostatic bearings and Standard deviation of instantaneous loading capacity图10 气浮支承平均承载力和瞬时承载力标准差

4.2 节流孔高度对微振动的影响

在保证其余参数不变的情况下，计算了当供气压力P1=0.5 MPa，节流孔倾斜角度β=110°，节流孔直径d=0.2 mm时，不同节流孔高度的气浮支承微振动特性.

图11所示为不同节流孔高度的气浮支承截面A的压力云图速度流线图和涡量云图.由图11可以看到，均压腔内湍流涡的数量随着节流孔高度的增加而减少.当节流孔高度在0.1~0.3 mm之间变动时，随着节流孔高度的增加，气体流线紊乱程度降低，均压腔内节流孔左侧湍流涡逐渐减少，节流孔右侧湍流涡在减少的同时其聚集区逐渐远离节流孔.当节流孔高度增加到0.4 mm时，节流孔右侧气体流线大部分平行于均压腔，均压腔内节流孔两侧的湍流涡继续减少，湍流涡聚集区基本消失.当节流孔高度继续增加时，均压腔内节流孔两侧的湍流涡基本保持不变.

Fig.11 Pressure nephogram and velocity streamline and vorticity nephogram of different orifice heights图11 不同节流孔高度下气浮支承压力云图速度流线图和涡量图

图12所示为不同节流孔高度下的气浮支承平均承载力及瞬时承载力标准差.由图12可以看到，气浮支承的承载力随节流孔高度的增加而略微减小.随着节流孔高度的增加气浮支承瞬时承载力的标准差逐渐减小，当节流孔高度增加到0.4 mm后，继续增加节流孔高度对气浮支承瞬时承载力的标准差基本没有影响.

Fig.12 Loading capacity of aerostatic bearings and its fluctuation standard deviation图12 气浮支承承载力及其波动标准差

4.3 节流孔直径对微振动的影响

在保证其余参数不变的情况下，计算了当供气压力P1=0.5 MPa，节流孔高度ha=0.4 mm，节流孔倾斜角度β=110°时，不同节流孔直径的气浮支承的微振动特性.

图13所示为不同供气压力下的气浮支承截面A的流线及压力分布云图和涡量云图.由图13可以看到，均压腔内的压力分布随着节流孔直径的增加而增加.随着节流孔直径的增加，气浮支承的湍流涡会随着节流孔直径的增加而减小.

Fig.13 Loading capacity of aerostatic bearings and its fluctuation standard deviation图13 气浮支承承载力及其波动标准差

图14所示为不同节流孔直径的气浮支承的平均承载力及瞬时承载力标准差.由图14可以看到，气浮支承的承载力随着节流孔直径的增加而增加，但平均承载力的增加趋势随节流孔直径的增加而减小.气浮支承瞬时承载力的标准差随节流孔直径的增加而减小.

Fig.14 Loading capacity of aerostatic bearings and its fluctuation standard deviation图14 气浮支承承载力及其波动标准差

4.4 供气压力对微振动的影响

在保证其余参数不变的情况下，计算了当节流孔高度ha=0.4 mm、节流孔倾斜角度β=110°以及节流孔直径d=0.2 mm时，不同供气压力下气浮支承的微振动特性.

图15所示为不同供气压力的气浮支承截面A的压力云图速度流线图和涡量云图.可以看到，均压腔内的压力分布随着供气压力的增加而增加.当供气压力在0.3~0.5 MPa之间变动时，随着供气压力的增加，气浮支承气体流线基本不发生变化，气浮支承涡量会随之增加.当供气压力继续增加时，气体流线会逐渐变得紊乱，均压腔内开始出现大量不规则的湍流涡.

Fig.15 Pressure nephogram and velocity streamline and vorticity nephogram of different supply pressure图15 不同供气压力的气浮支承压力云图速度流线图和涡量图

图16所示为不同供气压力的气浮支承平均承载力及瞬时承载力标准差.由图16可以看到，气浮支承的承载力随着供气压力的增加而增加，当供气压力在0.3~0.5 MPa之间变动时，气浮支承瞬时承载力的标准差随供气压力的增加而略微增大，当供气压力继续增加时，其瞬时承载力的标准差将大幅增大.

Fig.16 Loading capacity of aerostatic bearings and its fluctuation standard deviation图16 气浮支承承载力及其波动标准差

5 结论

a.基于湍流涡的形成机理，提出了1种新型多斜孔节流气浮支承，通过改变节流孔倾斜角度改善气浮支承流场特性，从而抑制湍流涡的产生.

b.采用大涡模拟方法分析了多斜孔节流气浮支承的瞬态流场特性，揭示了结构和工作参数对其微振动的影响规律.随着节流孔倾斜角度的增加，气浮支承微振动先减小再增大；气浮支承微振动随着节流孔直径、节流孔高度的增加而减小；随着供气压力的增大，气浮支承的微振动也随之增大.

c.在相同的供气压力下，当节流孔倾斜角度β=110°，节流孔高度ha=0.4 mm，节流孔直径d=0.2 mm时，气浮支承具有较好的稳定性.