掌握“ 归一问题”里的变与不变
文|徐曼玲
如何让更多的学生在理解“归一问题”中各数量关系的基础上,感受“归一问题里的变与不变”呢?
活动一:找归一
1.读一读:阅读信息:“妈妈买3 个碗用了18 元,_______?”学生尝试提出数学问题,如“妈妈买3 个碗用了18元,买5 个同样的碗用了多少元?”。
2.想一想:在这道题目中,什么是相同的?
活动二:画归一
1. 画一画:“妈妈买3 个碗用了18元,买5 个同样的碗用了多少元?”学生尝试用画图的方式来表达题意。
2.说一说:学生展示作品并分享自己的想法。
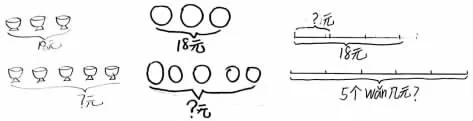
3.议一议:观察这三幅作品,你发现了什么?什么是不变的?
4.算一算:根据图示,列式(分步→综合)解答。
活动三:明归一
1.试一试:根据上面给出的信息,买更多的碗你还会计算吗?
买3 个碗用了18 元,__________?
2.理一理:不同数量碗的价格计算有相同之处吗?你能用一个算式表示出上面的这些碗的价格吗?学生尝试用字母n 表示碗的个数,表达碗的个数与价格的关系,(18÷3)n。
3.明本质:观察以上解决的这些问题,在问题解决过程中,什么没变?什么变了?学生发现,买碗的数量变了,但解决问题的方法不变,都是要先求出一个碗的价格是多少,再求出几个碗的价格是多少。教师明确,像这样,先求出一份量的问题叫作归一问题,这里的“一”就是指一份量或每份数。
活动四:用归一
1.想一想:思考:3 个杯子9 元,90元可以买几个同样的杯子?还有其他方法能解决这个问题吗?
2.比一比:学生交流两种方法。方法一,先算1 个杯子多少钱,再算90 元可以买几个杯子。方法二,先算90 元中有几个9 元,再算有几个杯子。学生发现,虽然先算的部分不同,但都是要先算出一份数,如先算1 个杯子,或者1 组杯子,然后再计算可以买几个。都运用了“归一”的方法。
活动五:创造归一
1.尝试创造:学生尝试自己编“归一”问题,并进行四人小组交流,互相判断是否为归一问题。
2.体悟内化:想一想,今天解决的归一问题有什么特点?如何可以准确找到不变的“一”?
通过以上读、写、画、算、议、理、创造等活动,学生经历了思考、判断、假设、验证、归纳等学习活动,不仅明晰了“归一问题”里的变与不变,更发展了辩证思考的数学思维和能力。

