聚焦真实情境 助推模型建立——以《鸽巢问题》教学为例

文|徐登池

一、问题反思：课堂教学的全方位审视

“鸽巢问题”也叫“狄利克雷原理”或“抽屉原理”，实际上是一种解决特定的数学或生活问题的模型，渗透着一种数学的思想方法，也体现了一种逻辑推理的能力。这其中的很多相关概念对于小学生而言，理解起来比较困难。通过前期对这类课的案例学习、课堂实践、课后分析，发现普遍存在以下一些问题，值得我们进一步深入探究。

1.教材内容有点分散，缺少结构化的设计

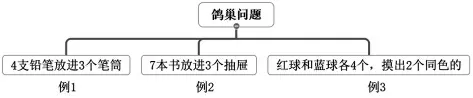
教材中编排了3 个例题，分3课时进行教学。仔细分析发现例1和例2 的内容其实是有关联的，例1 属于最简单的情况，例2 是“鸽巢问题”的一般形式。分两课时教学，知识点有点重复和分散，割裂了知识之间的联系，学生不能完整地经历建模的过程，缺少结构化的设计。

2.情境创设不够聚焦，不能激发学生需求

教材中提供的铅笔放到笔筒、书本放进抽屉的情境，对于小学生而言不会产生足够的学习兴趣，不能有效地激发他们的学习需求。同时，“总有……至少……”的句式本身理解起来就比较抽象，再结合这样的情境也不利于学生更好地理解其本质含义。如将4 支铅笔放到3 个笔筒里，为什么非要说“总有一个笔筒里至少有2 支铅笔”，有些学生总是不太明白，为什么不可以说“总有一个笔筒里至少有1 支铅笔”？

3.教学环节缺少层次，难以实现有序推进

由于教学内容本身的难度，教学设计不太贴近学生的最近发展区，以及教学环节层次缺少一定的梯度，导致学生的学习处于被动，在不断变换的情境中，只关注到“至少数=商+1”这个结论的记忆。虽然学生经历了多次动手操作，但是效果不太明显，尤其是余数不是1 的情况，为什么还要平均分的理解是一个难点。

4.学习效果相对单一，不能做到举一反三

学生学习了鸽巢问题，但是在解决其他相关的实际问题时，难以找到生活中的问题与鸽巢问题之间的联系。即便是找到了，也很难理解哪个是鸽子数，哪个是鸽巢数。

二、重组教材：教学内容的结构化设计

1. 基于学情，聚焦真实性情境，初步感悟模型

教材内容是一个范本，它所提供的例题也只是一个蓝本。我们不能拘泥于教材，可以跳出教材，寻找生活中与学生密切相关的素材作为研究学材，更有利于学生对鸽巢问题本质的理解。于是，我把教材中的情境“在笔筒里放铅笔”“在抽屉里放书”的问题，统一换成了一个大情境——车辆过红绿灯的问题。

片段一：分为三个层次

第一层次：

想一想：3 辆车停在2 个车道上，可以怎样排队停车？

写一写：用简洁的方式记录你的想法。

说一说：哪种情况下，3 辆车能最快通过红绿灯？同桌交流。

呈现学生资源：

方法1：用圆圈图来表示。

方法2：用数字来表示：3，0；2，1。

第二层次：

想一想：如果是4 辆、5 辆车停在2 个车道上，可以怎样排队停车？

写一写：用简洁的方式记录你的想法。

说一说：哪种情况下，4 辆、5辆车能最快通过红绿灯？同桌进行交流。

呈现学生资源：

方法1：画圆圈图。

方法2：用数字表示。

学生在两次操作活动中，很容易感受到用画圆圈图和数字这样的列举法都能简洁地表示出结果，解决了真实情境中的问题。并通过充分的对比、交流，初步得出要想车辆能快速通过红绿灯，就是要把这些车辆尽可能平均分到每个车道上。同时，原教材中的“总有……至少……”中的“总有”学生理解起来有困难，我们利用过红绿灯的情境，把它巧妙地替换成“最多”，如要想5 辆车最快通过红绿灯，车辆最多的车道上至少有3 辆车。这样的改变，学生理解起来更容易，同时也符合鸽巢问题的本质。

第三层次：

想一想：如果是15 辆？91 辆？m 辆车呢？

写一写：用简洁的方式记录你的想法。

说一说：哪种情况下，车辆能最快通过红绿灯？同桌交流。

呈现学生资源。

得出：m÷2=商……1，余下来的一辆任意放到两个车道中，车辆最多的车道至少有（商+余数）辆车。

有了前两个操作活动的铺垫，当车辆数越来越大时，学生发现不管是用画圆圈图，还是写数字的方法都比较麻烦，进而不断完善方法，直接列除法来计算，即均分法，能简洁地表示出结果。在若干次的枚举中，学生最终提炼出用一道式子“m÷2=商……1”来概括上面的所有情况。在这里重点点拨了此处的“1”是余数，于是提出了猜想“车辆最多的车道至少有（商+余数）辆车”。这样的设计，为后面的学习埋下伏笔，就是结论为什么是“至少数=商+1”，而不是“至少数=商+余数”。

2. 紧扣问题，设计进阶式任务，深入理解模型

在第一环节中，研究的车道数是2 个，余数只能是1 这一种情况。到了第二环节，车道数变成3 个，让学生自主经历研究过程，结合猜想进行大量举例验证，尤其是当余数不是1 时，学生容易产生思维定势，这也是本节课的一个教学难点。

片段二：

出示问题：（ ）辆车停在3个车道上，要想它们最快通过红绿灯，车辆最多的车道上至少有几辆车？

呈现学生不同的资源：

①5÷3=1（辆）……2（辆）,2÷2=1（辆），1+1=2（辆）。

②5÷3=1（辆）……2（辆）,1+2=3（辆）。

追问：这两个例子余数都是2，但结果却不一样？你同意谁的做法？

出示课件模拟停车的过程，指名学生在黑板上摆一摆。

学生有了猜想“至少数=商+余数”后，在验证环节中，会自然而然地认为结果就是3 辆。通过两种不同方法的对比，倒逼他们去思考哪种做法是正确的。同时利用多媒体课件演示，以及学生亲自到黑板上摆一摆，在此过程中让他们清楚地看到剩下的2 辆车还要继续再次平均分，这样才能达到“至少”的要求，如果放到同一个车道，就不能最快通过红绿灯了。这个教学难点的突破，紧紧扣住了“如何能最快通过红绿灯”这个问题，其实这也是鸽巢问题的本质。

3. 整合资源，运用结构化设计，逐步建立模型

原来的教材中，笔筒数和铅笔数这两个变量都在发生变化，不利于学生对规律的探究。同时，为了能让学生从整体上对本节课知识形成系统的认识，把教材中例1 和例2 的内容进行了重新调整与整合，整个核心过程始终围绕大情境“车辆过红绿灯的问题”设计了以下三个教学环节。

第一环节：m 辆车停在2 个车道上，哪种情况下车辆能最快通过红绿灯？

第二环节：m 辆车停在3 个车道上，哪种情况下车辆能最快通过红绿灯？

第三环节：m 辆车停在4、5、6个……车道上，哪种情况下车辆能最快通过红绿灯？

追问：像这样，能说得完吗？能用一道算式把上面的所有情况都表示了吗？

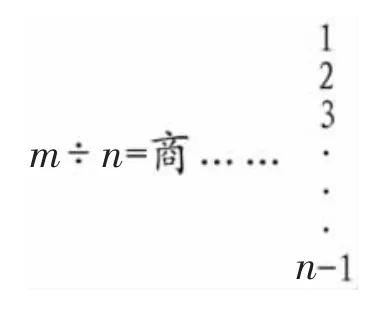
通过控制变量、有序研究的方法，让学生在自主探究中逐步发现规律。第一环节是教学结构，让学生思考、解决怎样停车能最快通过红绿灯，用列举法和均分法都能找到答案，初步感悟只要看车辆最多的车道上的车尽可能少就可以了。同时，得到了一个猜想：要想最快通过红绿灯，车辆最多的车道上至少有（商+余数）辆车。第二环节是在第一环节的基础上把车道数变成3 个，进一步验证是不是还存在这样的现象。最后，通过大量的举例验证，并用一道算式表示出所有情况（至少数=商+1），感受数学语言的简洁性。学生经历了“鸽巢问题”模型建构的过程，思维由外向内聚焦，由直观向推理发展，最终形成“鸽巢问题”的数学模型。

4. 灵活运用，通过变式性练习，不断丰富模型

当模型建好后，就要回到日常生活中，通过快速反应，运用今天的所学内容，主动地去找一找真实问题中谁是鸽子，谁是鸽巢。

片段三：

说一说：（ ）是鸽子，（ ）是鸽巢。并解释下面的说法对吗？

（1）8 个人坐3 把椅子，至少有一把椅子上坐了3 人。

（2）10 块巧克力放入4 个袋子里，至少有一个袋子里有2 块巧克力。

（3）六10 班有46 名同学，至少有4 个人是在同一个月出生的。

通过这样的练习设计，让学生进一步巩固和强化建立的模型，并感受到运用这样的模型来解释生活中的现实问题，进一步体会数学与生活的联系，以及培养学习数学的兴趣。

在整个教学中，真实的问题情境引入和直观的动手操作演示起到了非常重要的作用，是教师“教”和学生“学”的好帮手，是可视化呈现“鸽巢问题”的思维工具。学生在活动中经历了“观察猜想→举例验证→建立模型→丰富模型”的学习过程，把抽象难懂的数学知识变得直观、形象，让学生在愉快的学习过程中享受了成功的喜悦，数学的核心素养也在建模中逐步建立起来。