智慧教室环境下培养初中生数形结合思想的实践

陈国兴

数学是一门研究数量、结构、变化、空间、信息等概念的学科。数形结合思想中的“数”与“形”分别对应数量关系与几何图形，是数学学习中两项重要的内容。“数”“形”在一定条件下可以相互转化，数形结合思想是解决数学问题的重要思想方法之一。在初中阶段，培养学生的数形结合思想是落实核心素养培养任务的重要一环，而建设智慧教室，借助信息技术、互联网络等，打造直观化、具象化的课堂，可以极大增强培养学生数形结合思想的实效性。

一、智慧教室与数形结合思想

（一）智慧教室

智慧教室是以信息化技术与多媒体融合为载体，利用智慧学习设备打造的新型教室。其由两个核心部分组成：一是有形的物理空间，二是无形的数字信息空间。在智慧教室开展教学时，师生通过无线局域网络和多种类型的“智慧屏幕”，可以同时获取资源，随时进行互动，从而打造新型教学环境。

（二）数形结合思想

数形结合是将数量关系与几何图形结合在一起，借助数量的精确性描述，阐释几何图形的某些属性，或借助图形的直观性描述，阐释数量之间的关系，达到“以数解形”“以形助数”。在初中数学学习中，“数”与“形”是两个关键部分，数形结合思想体现了直观与抽象的统一，有助于学生在学习过程中将形象思维与抽象思维有机结合。

二、智慧教室环境下培养初中生数形结合思想的实践

（一）電教设备呈现，直观认识数形结合

有学者曾说：“数形结合百般好，割裂分家万事休。”可见数形结合在数学学科中的重要性。而智慧教室具备了直观呈现数形结合过程的条件，在智慧教室环境下，教师在教学中应从学生的形象思维出发，循序渐进地培养学生的数形结合思想。例如，在教授人教版初中数学七年级下册第九章第三节“一元一次不等式组”相关内容时，教师可以利用电教设备，完整呈现数形结合思想在解决一元一次不等式组中的应用，让学生直观地感受数形结合的思维过程。

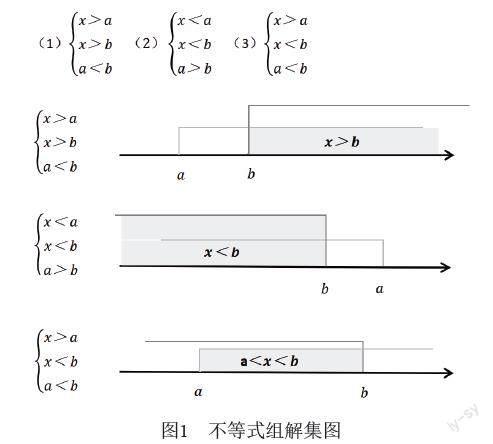
1.呈现主题，具象了解。教师可以向学生展示问题，让学生以数轴形式求出下列不等式组的解集：

在解题过程中，学生结合学过的不等式知识，在数轴上会发现以上不等式组的解集未出现重合，从而从“形”的角度对一元一次不等式组获得一定的认知。随着解题的深入，学生会总结出规律，即数大取大、数小取小、大小与小大时在中间找解、大大小小情况无解，从“数”的角度对一元一次不等式组产生更深的认知。

2.抽象符号，数形结合。教师可以利用电教设备，将上述不等式组用符号表达，并以数轴还原解集（图1）。教师还可以在多媒体屏幕上以动画形式，呈现还原解集过程中的每一个步骤，确保每一个步骤与数量关系对应，使学生充分感受数形结合的思维过程。

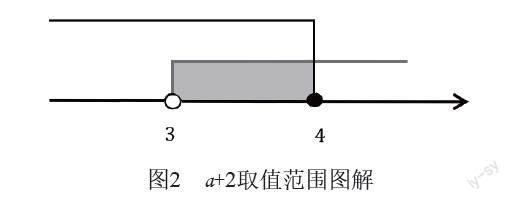
3.基础实践，直观体验。教师可以提出问题：“假设不等式x-2＜a有正整数解，能否借助数轴确定a的取值范围？”问题提出后，学生会通过数轴快速确定a的范围。在此基础上，教师可以逐步深化问题：“若不等式的正整数解有3个，该如何在数轴上确定？”在解答问题的过程中，学生先确定0≤x＜a+2，而解为正整数有3个，通过数轴可以看出在满足条件下a+2应介于3与4之间（图2）。为保证解为3个，a+2不能等于3，若等于3则只能保证有2个正整数解，a+2为4时则能够满足题目条件，因此，可以确定的取值范围为3＜a+2≤4，拆分成不等式组                 ，经过计算得出1＜a≤2。

在以上三个环节的学习中，教师在电教设备的辅助下，引导学生总结在解决数学问题时运用数形结合思想的方法，感受数形结合的优势，有助于学生在完整、直观的感知过程中，客观、全面地认识数形结合思想。

（二）智慧课堂互动，发展数形结合思维

智慧教室环境下的智慧课堂，是通过多媒体融合打造的高端课堂形态，能够为师生互动提供多种渠道。教师在教学实践中要充分利用智慧课堂的优势，与学生开展深度互动，引导学生运用数形结合思想看待问题、解决问题，培养学生的数形结合思维。例如，在人教版初中数学八年级上册第十二章第三节“角的平分线的性质”的学习中，学生需要掌握的知识包括通过三角形的角平分线构造全等三角形、证明三角形全等。在教学过程中，教师可以充分利用智慧教室中的电教设备，引导学生积极参与课堂互动，培养学生的数形结合思维。

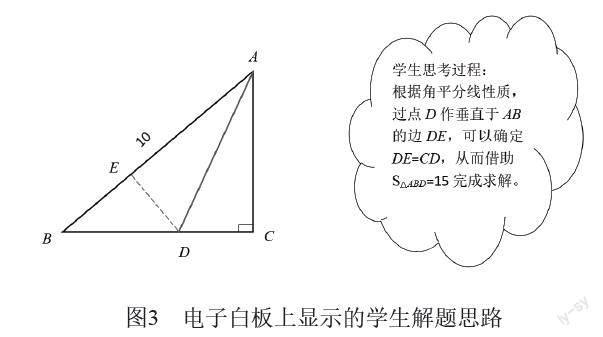
1.电子白板互动。教师可以在电子白板上向全班学生呈现如下例题，引发学生思考。例题1：“在△ABD中，已知∠C为90°，AD是∠BAC的平分线，与BC相交于点D。其中AB=10，S△ABD=15，求CD长。”

2.学生响应系统。教师可以利用手持设备询问学生关于解答例题1的思路。这样，学生可以单独回答教师的问题，避免干扰其他同学的思路。在此过程中，教师可以将知识条件体现在题目的图示中，更深入地挖掘题目的已知信息，帮助学生更直观地理解已知条件与数量关系。

3.互动投影。在确定解题思路后，学生可以利用手势在电子白板显示的课件上通过拖拽、画图等方式完成操作，将自身基于数形结合思想的思考呈现在电子白板上（图3）。其他学生有了新的解题思路时，也可以在电子白板上利用不同颜色的线条或文字进行表达，给予学生充分参与课堂的机会。

4.平板电脑互动。学生可以按照上个环节确定的解题思路，在平板电脑上写出解题过程并上传至学习平台，教师与其他学生均可同步看到答案。基于此，学生之间可以实现共享和交流，并在此过程中学习数学语言的表述，加深对数形结合的理解。

在智慧课堂，多样化的互动途径能够为学生提供体验数形结合的契机，促进学生基于数形结合展开丰富且有深度的交流，从而保证学生充分参与课堂，实现数形结合思维的有效发展。

（三）人机交互练习，强化数形结合意识

在练习中感知数形结合，是学生快速形成数形结合意识，自觉利用数形结合思考与解决问题的重要路径。在智慧教室环境下，人机交互练习方式摆脱了枯燥、机械的传统练习模式，有利于激发学生的练习兴趣。在此过程中，教师要高效分享资源、实时互动，密切关注不同层次学生的练习需求。教师在传递习题资源时，可以设置不同难度的模块，告知学生可以根据需求先从基础模块做起，攻克基础题目后再挑战中级题目，在进阶式的练习中持续增强学生的数形结合意识。

例如，在教授人教版初中数学九年级下册第二十六章“反比例函数”之后，教师可以在线上学习平台上传包含反比例函数基础知识、与一次或二次函数结合、与几何图形结合、与实际生活结合的练习题。其中，基础知识及与一次或二次函数结合的习题为基础题目，与几何图形结合的习题为中级题目，与实际生活结合的习题为高级题目。学生在学习平台上找到习题库后，点击对应标题即可获取习题资源。在学生做题的过程中，教师通过线上平台可以随时掌握学生的答题情况。当观察到全部学生完成了基础习题、绝大多数学生完成了中级习题，且10分鐘时间内高级习题正确率未上升时，教师可以直接在线上平台切换角色，选择一名做对习题的学生当“小老师”，在学习平台上演示高级习题的解题思路、过程，方便学生彼此借鉴数形结合思想方法的运用经验，弥补知识和认识上的不足。

（四）多屏协同共享，发散数形结合思维

智慧教室环境下，教学空间与资源不再受限，教师在课堂上可以基于多屏共享拓宽学生视野，从多方面渗透数形结合思想，培养学生的发散思维，提高学生举一反三、触类旁通的能力。例如，在人教版初中数学九年级上册第二十四章第二节“点和圆、直线和圆的位置关系”的教学中，为了延伸课堂，教师可以基于教师用屏、小组用屏和学生用屏，引导学生探索知识，应用数形结合思维解答问题。

首先，在教师用屏上，呈现核心知识点与数学问题。教师可以将学生自主绘制的思维导图呈现在教师用屏上，并设置如下题目。

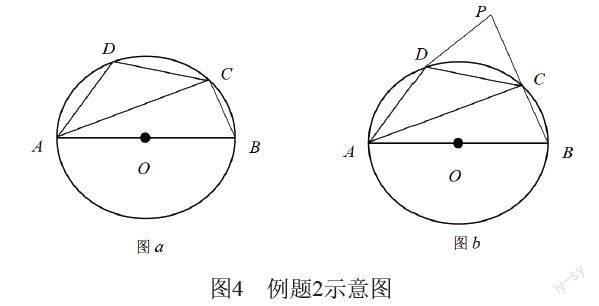
例题2：如图4，四边形ABCD内接于⊙O，AB为⊙O直径，已知AD=CD.

1.根据图a，求证∠ABC=2∠ACD；

2.如图b，过点D作⊙O切线，交BC延长线于点P，假设tan∠CAB=，BC=1，求PD长。

其次，在小组用屏上（教室墙面上安装的可触摸一体机），要求学生以小组探究形式解决题目。学生可以应用小组用屏，将数量与图形之间的关系直观地呈现在屏幕上。例如，有小组在解决例题2时，通过小组用屏直接连接OD与OC，发现了解题突破口。但有小组经过反复尝试未能发现解答∠ABC与∠ACD之间关系的突破口。此时，学生可以点击屏幕上的“提示”功能键，教师在收到消息后，可以及时为该小组传递资源给予提示，如其他组的解题思路等。

最后，在学生用屏上，教师可以通过局域网共享各个小组的探究成果，以视频的方式呈现小组探究中的一系列学习行为，实现深层交互，从而提高学生对数形结合思想的应用能力，促进学生发散思维。如大多数小组在解决例题2时做了辅助线OD，但有个别学生提出“不做辅助线的情况下能否求解”这一问题。针对该问题，各小组重新梳理图形与数量之间的关系，探索新的解题方法，进一步加深了对数形结合思想的理解。

（作者单位：福清市高山育才中学）