淡水河一维-二维耦合水动力学模型构建及应用

钟 华

(广东省水文局惠州水文分局，广东 惠州 516003)

为做好新形势下淡水河流域暴雨洪水的防灾减灾技术支撑，补齐工作技术短板，实现淡水河主城区洪水风险快速分析与评估，以淡水河两岸的惠州市惠阳区主城区为示范区域，建立基于高速计算的惠阳区洪灾实时分析。淡水河及其两岸防洪保护区的溃堤及漫堤洪水演进过程，涉及淡水河及支流与两岸防洪保护区之间的复杂水力关系[1]。与水文学法相比，水力学法能准确模拟溃堤及漫堤洪水的动态演进过程，同时，由于研究区域具有较为翔实的水文、地形等基础数据，为建立区域水力学模型奠定重要的数据基础，因此淡水河洪水演进选择水力学方法构建洪水模拟模型。当前，国内主要采用不同维度的水力学模型进行区域洪水演进[2-15]，其中可通过计算边界的耦合来实现不同维度水力学模型的动态耦合。若堤防规模较大，溃口处洪水的流态与宽顶堰流较为接近，因此因此传统方法采用宽顶堰流公式计算溃口流量。然后对于传统溃口流量的洪水演进算法由于不能对耦合模型之间的动量方程进行相对准确的表达，使得其计算中对于流量系数的选取存在很多不确定性，降低了模型计算的精度。此外由于传统溃口流量计算方法常常对溃口位置进行概化处理，对于溃口位置较为复杂的洪水演进计算其计算适用性不高。此外，当堤防或溃口两侧水位差较大时，基于宽顶堰流公式计算的溃口流量偏大，极易导致河段水位波动大、计算失稳。为解决河段水位波动大的问题，往往需要设置更小的计算时间步长，从而极大降低模型计算效率。为提高淡水河洪水演进的精度，通过侧向联解的方式实现一维河网模型与二维浅水模型的耦合。研究成果对于实现淡水洪水淹没和洪灾评估的快速计算分析具有较强的实践指导意义。

1 耦合模型构建原理

传统方法溃口流量计算方程为：

(1)

式中，Q—断面模拟的流量计算值，m3/s；z1d和z2d—耦合模型边界水位计算值，m；zw—边界耦合处计算断面底部高程，m；Cd—计算参数变量，主要对计算流量影响较大；L—溃口概化形状的宽度，m。

将一维、二维水动力学模型采用侧向联解的方式进行耦合计算，即通过水力因子进行耦合边界的水位、流量变量进行耦合，具体耦合过程如图1所示。耦合边界为不同计算相邻断面之间的河道边界。

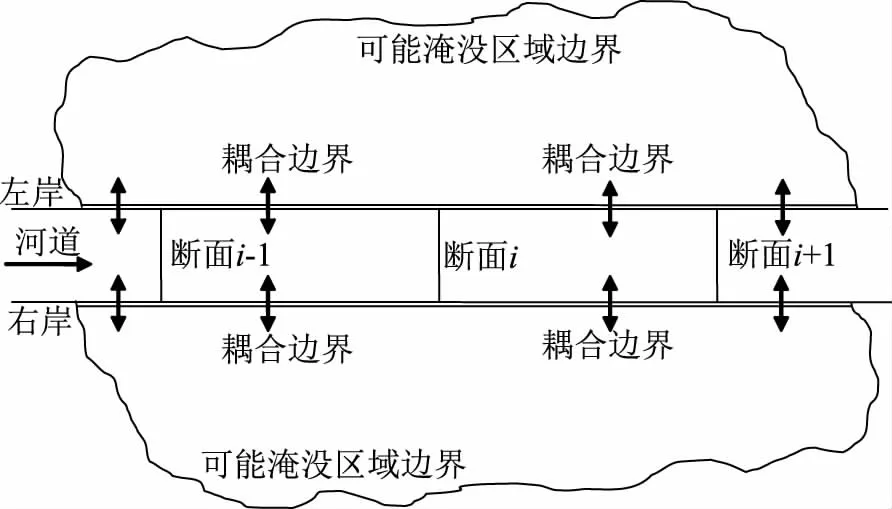
图1 一维-二维模型耦合方式示意图

首先计算一维水动力学模型在进行耦合模型求解时，将不同维度模型计算的变量在耦合边界进行水力因子的传递后再进行二维水动力学的模拟计算，一维模型的上断面输入采用旁侧入流的方式将耦合边界的流量进行传递计算。

由于耦合水力学模型具有差异较大的计算时段间隔，因此采用二维水动力学模型进行计算时需要对时间间隔进行自适应的调整从而提高耦合模型的计算效率。二维模型的计算时间间隔通常要高于一维水动力学模型的计算时间间隔，因此按照相对较为固定的时间间隔来作为一个基准对耦合模型的计算间隔进行调整。当前时刻t更新至下一时刻t+Δt1的断面计算水力学因子首先通过一维水动力学模型进行上断面传递，随后当耦合模型计算步长达到m步后，通过边界约束条件控制上一步计算步长内的时间间隔相应调整为：

(2)

式中，Δt1d—相对较为固定的一维水动力学模型计算时间间隔，h；Δt2d—相对较为固定的二维水动力学模型计算时间间隔，h；m—耦合模型计算步长总数，个。

按照二维水动力学模型对耦合模型计算时间间隔最大值进行条件动态控制。不同维度水力学模型耦合计算步长差异性可通过动态调整计算间隔来进行匹配。

2 模型应用

2.1 模型构建

耦合边界主要为一维、二维水动力学模型各相邻计算断面之间的河道边界。水位边界为耦合模型的主要计算边界，河道上下游相邻断面的水位控制节点输入主要通过距离插值计算得到。旁侧入流为一维水动力学模型的耦合边界。为兼顾模型的计算精度及计算效率，采用不同空间分辨率非结构三角网格嵌套的方式进行项目区的网格剖分，在淡水河沿岸采用较密网格，其他区域采用较疏网格。共剖分网格38833个，网格边长15～80m。网格剖分结果如图2所示。

图2 网格剖分结果

2.2 模型率定

考虑地形及水文资料的实际条件，选取2019年7月10—11日水文测验的实测水位、流量对一维模型进行率定。作为参数率定的比对参考包括：淡水站、永湖桥、三和大桥3个断面，基本覆盖了淡水河惠阳城区、下游三和、永湖镇区的主要断面。模型的初始糙率值参照《惠阳区淡水河干流防洪排涝规划》的糙率成果，综合考虑桥梁阻水作用等因素，对照本次实测流量、水位过程线进行糙率调整，最终率定后代表典型断面的河道综合糙率见表1。

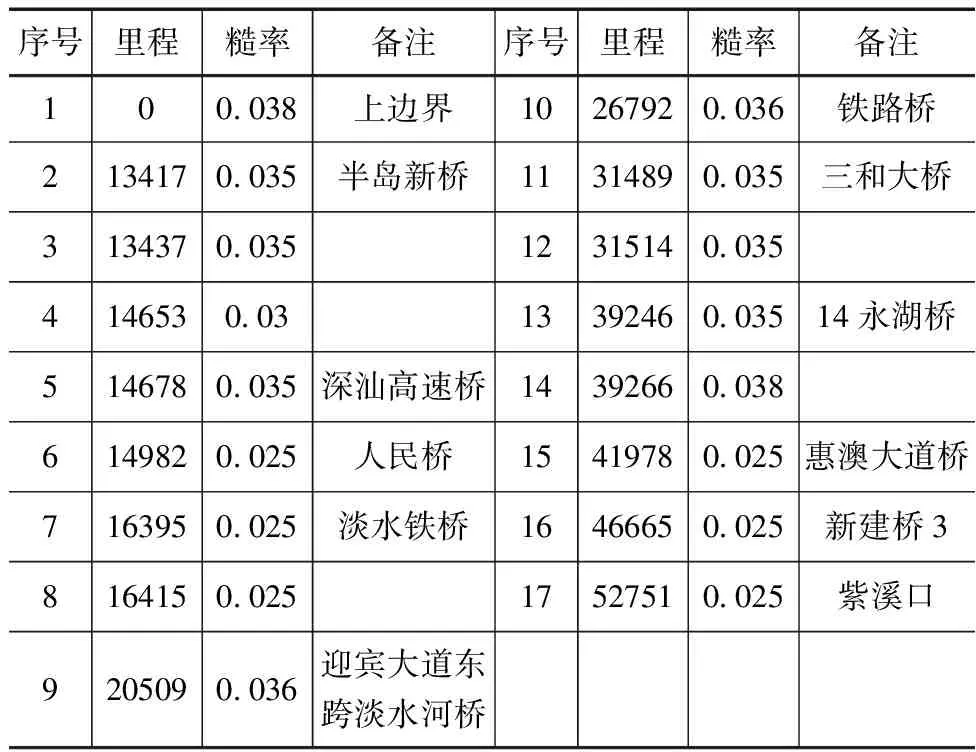
表1 模型率定糙率成果

2.3 模型验证

采用2018年9月17日山竹台风期间的洪水调查洪痕，以及上游白石、樟埔、维布和下游的出口的水贝站实测水位过程，以上游3个站点的水位流量关系将水位过程转化成流量过程，沿程按集雨面积比例加入流量，对模型进行验证。验证结果见表2。

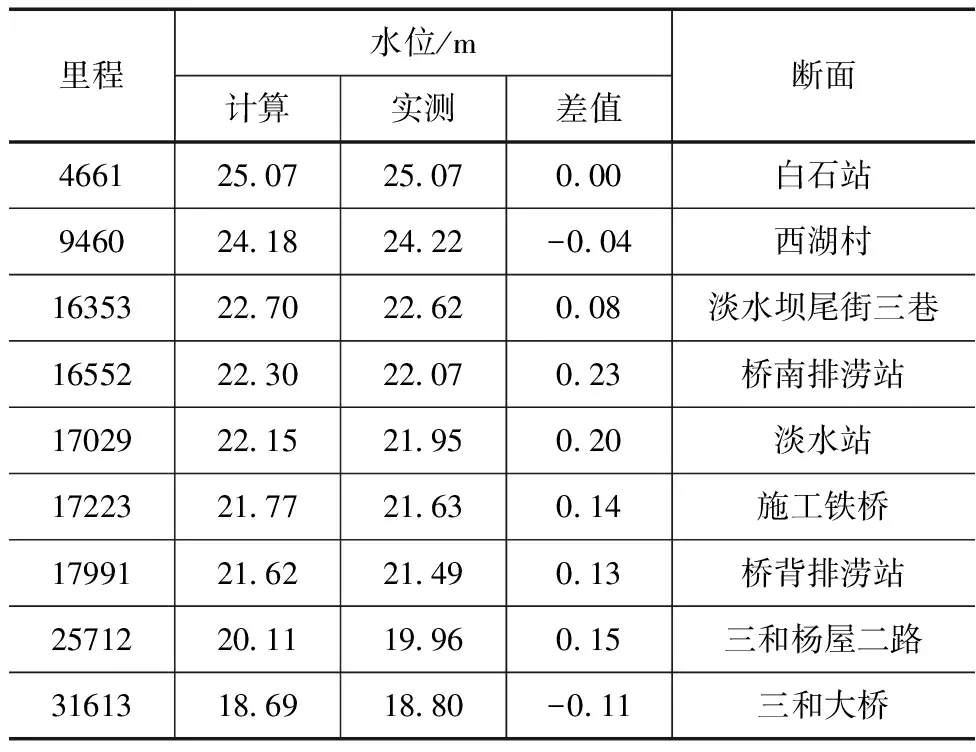
表2 模型验证成果

从验证结果可以看出，桥南排涝站到淡水站河段，水面线误差在20cm以上，这是由于“山竹”期间，铁桥处缺口发生漫溢，导致实际水位相对偏低，其余河段水面线偏差均在20cm以内，说明模型计算结果相对合理。

3 结论

(1)堤防或溃口两侧水位差较大时，基于宽顶堰流公式计算的溃口流量偏大，极易导致河段水位波动大、计算失稳。为解决河段水位波动大的问题，建议设置更小的计算时间步长，从而极大降低模型计算效率。

(2)不同尺度水动力模型的计算时间步长差异较大。为提高计算效率，在进行模型耦合计算时，二维模型应选择基于自适应时间步长模式。考虑到一维模型时间步长往往要远大于二维模型时间步长，故以一维模型的固定时间步长为基准，二维模型时间步长进行自适应匹配。

(3)本文未考虑断面间距对模型计算精度的影响，存在不足，在后续的研究中应重点考虑断面计算步长对耦合模型精度的影响。