平均值法交流共模抑制比测量不确定度评定

梁志国, 冯秀娟

(1. 北京长城计量测试技术研究所 计量与校准技术重点实验室，北京 100095；2. 中国计量科学研究院 力学与声学计量科学研究所，北京 100029)

1 引 言

共模抑制比是表征具有差分输入特征的测量仪器系统对共模干扰抑制能力的指标参数[1～4],在电磁环境极为恶劣的大工业现场,属于主要干扰源之一。通常,用于温度、应变等量值测量的仪器设备,其量程范围为伏特、毫伏量级,分辨力在毫伏甚至微伏水平。而工业现场的工频共模电压,在大型动力设备的启动、停止和运行期间,往往能达到几百伏甚至上千伏的水平。由此导致,一些数据采集系统、瞬态记录仪器等数字化测量仪器设备是否能够适应工业现场的应用,其抗共模电压范围以及共模干扰的抑制能力成为其最主要因素。因此,共模抑制比是最重要的抗干扰指标参数。由于是抗干扰指标,其受重视程度远低于测量误差等参数,加之抗干扰参数本身的测量离散性较大,导致该类特性测量研究较少,不确定度评定文献更加缺乏。

与数据采集系统相比,以技术更加成熟的数字多用表为例,目前,在我国共有3份权威文献[10～12]对其指标参数进行表征,2份是国家标准,1份是计量校准规范。仅仅在标准中对共模抑制比的测量评价进行了阐述,使用共模干扰峰值幅度与其产生的波动量值之比的对数形式进行表征,波动量值及其表现形式如何确定及定量赋值,并未具体给出,而国家计量校准规范则没有进行共模抑制比的计量校准项目。这些情况,均将造成共模抑制比测量评价的困惑。

共模干扰属于何种波形?是交流?直流?或者噪声?是非平稳?平稳?或者毛刺尖峰?并无统一一致的结论。场合不同,面对的干扰源不同,波形也会截然不同。通常认为,它既可能属于交流叠加形式,也可能表现为直流累加形式,进而也体现出噪声叠加多寡的形式。同时,还可能表征为叠加尖刺与杂波等多种非平稳方式。能同时表述这些不同信号的共性特征,具有良好稳定性与复现性的参数,首推干扰有效值,用均方根幅度表述;其次为干扰波形覆盖面积,用幅度绝对值的均值表征。本文后续内容,以数据采集系统交流共模抑制比的平均值方法为对象,进行测量不确定度评定。

2 交流共模抑制比测量原理与方法

共模干扰评价中,核心问题有两个,一为干扰信号量值如何表征;即,是用有效值?峰值?或者平均值?二是如何剔除本底噪声?以便精确量化干扰强度;即,是用功率差方式还是用幅度差方式剔除;幅度差方式用幅度直接相减获得结果,功率差方式用幅度平方和相减获得结果。

针对非常微弱的本底噪声时,不同剔除方式差异不大,而当干扰信号幅度与本底噪声幅度相近时,结果差异非常明显。

本文后续部分使用幅度绝对值的平均值表征干扰强度,用代数差方式剔除本底噪声影响。

如图1所示接线,将数据采集系统被测通道的两个差分输入端用1 kΩ的电阻R端接[1,2],称为不平衡电阻,将共模信号发生器的“高”端连接到电阻R的一端;共模信号发生器的“低”端与被测数据采集系统的外壳“地”相连,并接到“大地”。

图1 数据采集系统共模抑制比校准连线图Fig.1 CMRR calibration diagram of data acquisition system

选取测量通道为最小量程档,通道增益G。

使共模信号源输出为零,获得本底噪声采集数据x0i,(i=0,…,n-1)。

选定共模信号频率f,一般为工频50 Hz(或 60 Hz),将共模信号幅度有效值EA由小到大缓慢增加,直到采集数据与本底噪声相比有较大变化,获得整数个半周波的共模干扰采集数据xAi,(i=0,…,n-1)。

按式(1)～式(8)计算通道的交流共模抑制比CMRR。

本底均值:

(1)

本底噪声幅度绝对值:

(2)

本底噪声幅度绝对值均值:

(3)

有干扰后响应幅度绝对值:

(4)

有干扰后响应幅度绝对值均值:

(5)

(6)

剔除本底影响的干扰响应幅度绝对值标准差:

(7)

(8)

3 测量不确定度模型

由式(8)微分得:

(9)

其灵敏系数[10]:

(10)

(11)

(12)

(13)

则,由式(9)可知共模抑制比CMRR测量不确定度的主要来源为:

(1) 共模信号幅度的不确定度u(ES);

(2) 测量通道增益G的不确定度u(G);

(5) 共模抑制比CMRR测量重复性带来的不确定度uA。

假设各个不确定度分量互不相关,得共模抑制比CMRR测量不确定度模型如式(14)所示[10]:

(14)

4 测量数据及处理

使用FLUKE 9500A型示波器校准仪作为共模激励源,其指标为[11]:

幅度范围:1 mV～100 V

幅度最大允许误差:±0.006%～±0.003%

频率范围:10 Hz～1 MHz

频率最大允许误差:±5.0×10-5

总失真度:≤-60 dB

使用NI USB 6210型数据采集系统作为被测对象进行共模抑制比实验。其指标为[7]:

ADC位数b=16位,差分输入通道8个,最高采样速率250 kSa/s;

四档输入量程范围:±0.2 V、±1 V、±5 V、±10 V;

模拟输入最大电压(信号+共模):±10.4 V;

模拟带宽122.5 kHz,存储深度为n=4096点数据FIFO;

幅度最大允许误差(满度点):±88 μV、±310 μV、±1.41 mV、±2.69 mV;

随机噪声标准差:12 μV、26 μV、118 μV、229 μV;

偏移最大允许误差:±4.0×10-5、±2.5×10-5、±2.0×10-5、±2.0×10-5;

增益最大允许误差:±1.35×10-4、±9.5×10-5、±8.5×10-5、±7.5×10-5;

CMRR(DC至60 Hz):100 dB。

选取NI USB 6210的通道1为共模干扰激励测量通道,加载峰值Es=5 V、频率50 Hz的正弦信号作为共模干扰激励信号。

选取量程范围为±0.2 V,标称增益G=1,采集速率为250 kSa/s,不平衡电阻R=1 kΩ,存储深度为n=10 000点。

共模信号源的高端K分别接A、B端,执行上述CMRR测量,获得共模抑制比测量结果见表1。

表1 交流共模抑制比测量结果Tab.1 AC common mode rejection ratio measurement results

在共模抑制比校准中,规定选取量值较差的结果作为测量结果。不失一般性,仅针对K接A端情况进行不确定度评定,接B时可等同处理。

此时,本底噪声测量序列{x0i}和共模干扰测量序列{xAi}的曲线如图2和图3所示。

图2 本底噪声测量序列{x0i}曲线图Fig.2 Background noise sequence {x0i} curve

图3 共模干扰测量序列{xAi}曲线图Fig.3 Common mode interference sequence {xAi} curve

测量通道增益G不确定度u(G),可使用如下2种方式评定。

当使用说明书的标称增益G计算CMRR时,可用说明书提供的G的不确定度。

当使用自测量增益值G计算CMRR时,应对G测量值进行不确定度评定。具体可参考相应文献[12,13]。

由通道增益G=1.001 2可以计算获得[12,13],c2=8.675 479。由被测NI USB 6210的技术文件(参考文献[14]),知其增益最大允许误差为±1.35×10-4,设其在[-1.35×10-4,1.35×10-4]内服从均匀分布,则有:

其自由度ν(G)=∞。

共模激励信号峰值Es不确定度u(Es),通过激励源技术指标获取,设Es的误差在其最大允许误差区间[-Δ1,Δ1]内服从均匀分布,则u(Es):

(15)

按激励源说明书(参考文献[11]),50 Hz频率时,激励幅度5 V的最大允许误差±Δ1=±0.3 mV,则有:

u(Es)=0.173 2 mV。c1=1.737 178 dB/V。

其自由度ν(Es)=∞。

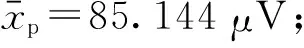
共模干扰测量值幅值xpi不确定度u(xpi)由xpi的实验标准偏差s(xpi)和测量分辨力Δ2不确定度u(Δ2)的最大值给出。

由被测NI USB 6210的A/D位数为b=16 bit,工作量程±0.2 V,可得量化阶梯误差Δ2=2×0.2/2b=6.10 μV,设量化误差在区间[-Δ2,Δ2]内均匀分布,则量化误差带来的不确定度u(Δ2)=Δ2/1.732=3.524 μV,其自由度ν(Δ2)=∞。

u(xpi)=max{s(xpi),u(Δ2)}
u(xpi)=72.500 μV

(16)

(17)

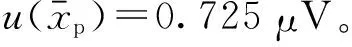
本底噪声测量值幅值xzi不确定度u(xzi),由xzi的实验标准偏差s(xzi)和测量分辨力Δ2不确定度u(Δ2)的最大值给出。

u(xzi)=max{s(xzi),u(Δ2)}
u(xzi)=41.613 μV

(18)

(19)

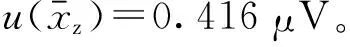
c3=-260.712 dB/mV,c4=260.712 dB/mV。

CMRR的测量重复性带来的不确定度uA。由表1的m次实验按式(20)给出实验标准差。

(20)

则uA=0.547 dB,其自由度νA=m-1=9。

5 合成不确定度计算

上述各不确定度分量列表如表2所示。

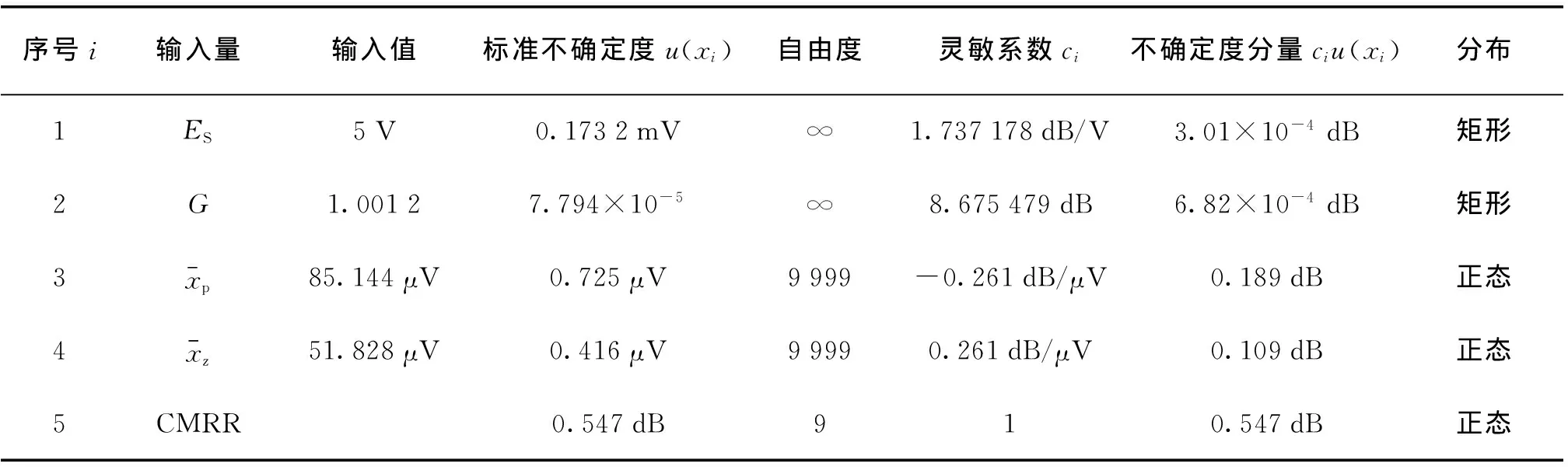
表2 不确定度分量概算表Tab.2 Estimate Table of Uncertainty Components

按式(14)计算CMRR的合成标准不确定度uc=0.59 dB。由表2可见,通道增益G和共模幅度ES带来的不确定度影响较小,可忽略。而其它3项因素均可对测量不确定度带来显著影响,且重复性为主导分量,由此,可以判定uc服从正态分布,按式(21)计算其有效自由度[5]:

(21)

6 扩展不确定度及测量结果的最终表述

选取置信概率p=95%,由有效自由度νeff(CMRR)=12,从t分布表查得包含因子k=2.179,则可得K接A时,CMRR的扩展不确定度:

U(CMRR)=k×uc=1.3 dB

共模抑制比为

CMRR0=99.6±1.3
(k=2.179,p=95%)

其中,±后面是扩展不确定度,它的包含因子为k=2.179,是置信概率p=95%的情况下,由t分布表查得。

7 讨 论

本文上述方法,使用的是平均值响应法进行共模抑制比计算,而数字多用表的国家标准等文件约定的共模抑制比的计算公式均强调的是共模干扰与其响应的峰值幅度比[10,11],从形式上两者是存在差异的。其主要原因有:1) 数字多用表共有3种测量原理,分别是有效值响应原理、峰值响应原理和平均值响应原理,而本文所述方法借鉴了数字多用表平均值响应原理的基本思想,用于给共模响应进行赋值,从技术上是有源头和借鉴出处的。2) 就峰值响应、有效值响应和平均值响应这3种测量原理而言,面对确定信号进行测量时,差异不大;但面向离散性和跳动性比较大的干扰响应波形而言,峰值法获得的结果的重复性要差很多,从上述图2和图3所述的实测曲线也能看到这些现象,而有效值法和均值法的重复性及稳定性要优良得多;因此,在比较看重重复性与复现性的计量校准中,后两者的处理方式更能显示出优越性,更加便于在计量校准中予以应用。

8 结束语

综上所述,数据采集系统的交流共模抑制比测量时,影响结果的不确定度的因素,主要涉及到系统增益、激励幅度的不确定度、测量误差、测量分辨力及测量重复性等要素。

从图2、图3可见,本文所述实验,共模干扰主要是以噪声幅度增加方式体现的交流干扰特性,未见明显的交流分量叠加以及直流分量增加趋势。

本文所述测量过程中,起主要作用的因素有测量量化分辨力和测量重复性,这些分量占绝对优势,而系统增益、共模激励幅度的影响可以忽略。因而,在通常的估计时,可以通过测量重复性和量化分辨力进行不确定度的基本估计。