基于改进白骨顶鸡优化算法的ECT图像重建

张立峰, 陈 达

(华北电力大学 自动化系，河北 保定 071003)

1 引 言

电容层析成像技术(electrical capacitance tomography, ECT)是最早发展起来的一种过程成像技术,具有结构简单、无辐射危害、价格便宜、易实现等优点,具有广泛的应用前景[1,2]。

ECT系统一般由电容传感器阵列、电容测量系统以及图像重建系统3部分组成。其中图像重建系统是ECT中非常关键的部分,图像重建问题的不适定性是获得场域内介质真实空间分布的难点[3]。目前常见的图像重建算法可分为直接算法、迭代算法、智能优化算法。直接算法包括线性反投影算法(linear back projection, LBP)[4]、Tikhonov正则化算法[5]等;迭代算法包括Landweber算法[6]、ART代数重建算法等[7]。其中,LBP算法原理简单、成像速度快,但成像精度低;Tikhonov算法收敛稳定但解过于光滑;Landweber算法和ART代数重建算法的重建精度要高于LBP算法和Tikhonov算法,但伴有明显的伪影。针对直接算法和迭代算法存在的不足,近年来广大学者将智能优化算法应用于图像重建中。张立峰等将极限学习机运用到电容层析成像中,重建图像精度和边缘保真度均优于传统直接算法和迭代算法[8];赵玉磊等运用双粒子群协同优化的方法,消除了ECT重建过程中因忽略“软场”效应而产生的影响,提高了重建图像精度[9];杜宇宁在ECT图像重建中将遗传算法和蚁群算法结合在一起,有效降低了重建图像与原始图像的相对误差[10]。

白骨顶鸡优化算法(coot optimization algorithm, COA)是Iraj Naruei等于2021年根据模拟白骨顶鸡在水中的集体运动提出的一种新研究的群体智能优化算法[11],与粒子群优化算法、鲸鱼优化算法和灰狼优化算法等大部分群体智能优化算法相比,能够更有效地求解高维非线性问题。为提高ECT图像重建精度,本文提出一种基于改进白骨顶鸡优化算法的ECT图像重建方法,该算法在开始阶段有较强的全局寻优能力,在后期能够有效跳出局部最优,并考虑了“软场”效应对图像重建造成的误差。最后,通过对单泡、两泡、三泡、环流和层流5种常见的油/气两相分布模型进行仿真和静态实验来验证本文算法的有效性。实验结果表明,本文算法对所研究分布模型的重建质量均有提高。

2 ECT原理

电容层析成像技术根据被测物质各相具有不同的介电常数,通过检测管道中不同物质所对应的介电常数分布,获得管道横截面的流体状况。从理论上而言,ECT图像重建属于对介电常数分布向量的求解过程[12]。

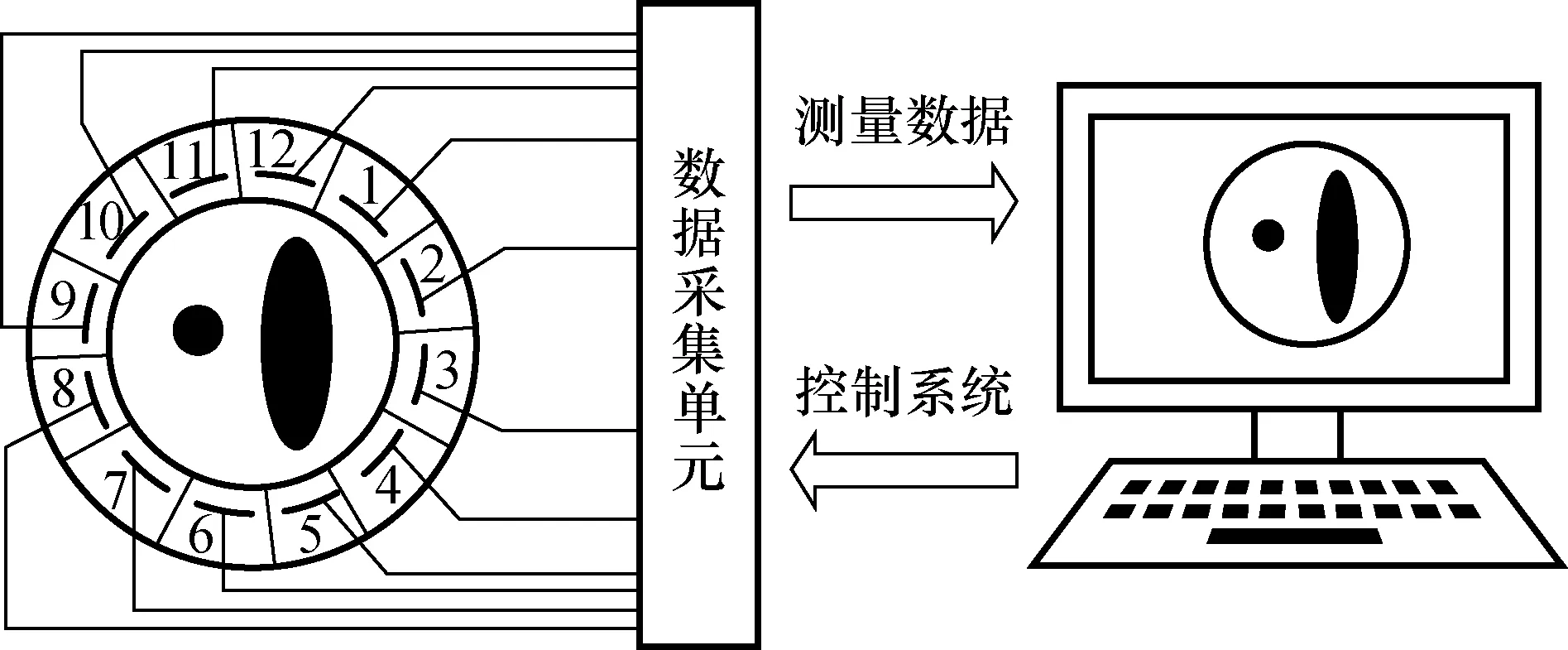
图1 电容层析成像系统示意图Fig.1 Diagram of the electrical capacitance tomography system

由电磁场理论可得施加电压后被测场内静电场满足拉普拉斯方程:

[ε(x,y)φ(x,y)]=0

(1)

式中:(x,y)为被测场内各点的坐标;ε(x,y)为(x,y)点的相对介电常数;φ(x,y)为(x,y)点的电位。式(1)的边界条件为:

(2)

式中:U为边界激励电压;Γi为电极i所在的空间位置;Γs为屏蔽罩的位置;Γg为保护电极位置。

电极间的电容值与相对介电常数的关系为:

C=f(ε)

(3)

对式(3)进行泰勒展开,忽略高阶项并进行归一化处理可得:

Sg=C

(4)

式中:S为n×m的归一化的灵敏度矩阵;g为m×1的归一化介电常数矩阵;C为n×1归一化电容数据矢量矩阵;n为独立测量的电极对数;m为场域剖分单元数。

3 白骨顶鸡优化算法

3.1 标准白骨顶鸡优化算法

白骨顶鸡优化算法是将白骨顶鸡种群分为领导者、跟随者,主要模拟了白骨顶鸡在水中的两种不同运动模式,即无序运动和同步运动,并将这两种运动模拟为算法中的3种行为:个体随机移动、链式运动、最优个体引导。

1)个体随机移动

初始化种群时,给每个个体选定一个随机位置作为参照:

Q=rand(1,d)*(ub-lb)+lb

(5)

式中:ub和lb分别为搜索空间的上、下限;d为求解维度。

个体的新位置更新方式为:

CootPos(i)=CootPos(i)+A×R2×

(Q-CootPos(i))

(6)

式中:i为当前个体的序号;R2为随机数或含有m个元素的随机序列,取值范围为[0,1];A的更新公式为:

(7)

式中:L为当前迭代次数;Iter为最大迭代次数。

2)链式运动

跟随者可根据两个个体的平均位置来执行链式运动:

CootPos(i)=0.5×(CootPos(i-1)+

CootPos(i))

(8)

3)最优个体引导

在有序运动过程中,跟随者的位置也可根据选定某一领导者的位置来进行更新。跟随者以领导者为圆心,在不同半径的的范围内进行搜索,以寻求更好的位置:

CootPos(i)=LeaderPos(k)+2×R1×cos(2Rπ)×

(LeaderPos(k)-CootPos(i))

(9)

式中:LeaderPos(k)为第k个领导者的位置;cos(2Rπ)控制跟随者与领导者间的角度,算法考虑了角度的逆向取值和正向取值,故角度范围为[-2π,2π];R1和R为两个随机数或两个含有m个元素的随机序列,R1的取值范围为[0,1],R的取值范围为[-1,1];k的计算公式为:

k=1+(iMODNL)

(10)

式中:NL为领导者的数量。

领导者的位置根据种群中最优个体的位置进行更新:

(11)

式中:gBest为中群内最有个体的位置;R3和R为两随机数或两个含有m个元素的随机序列,R3取值范围为[0,1],R的取值范围为[-1,1];R4为[0,1]内的一个随机数;B的计算公式为:

(12)

式中:L为当前迭代次数;Iter为最大迭代次数。

标准COA具体流程图如图2所示。

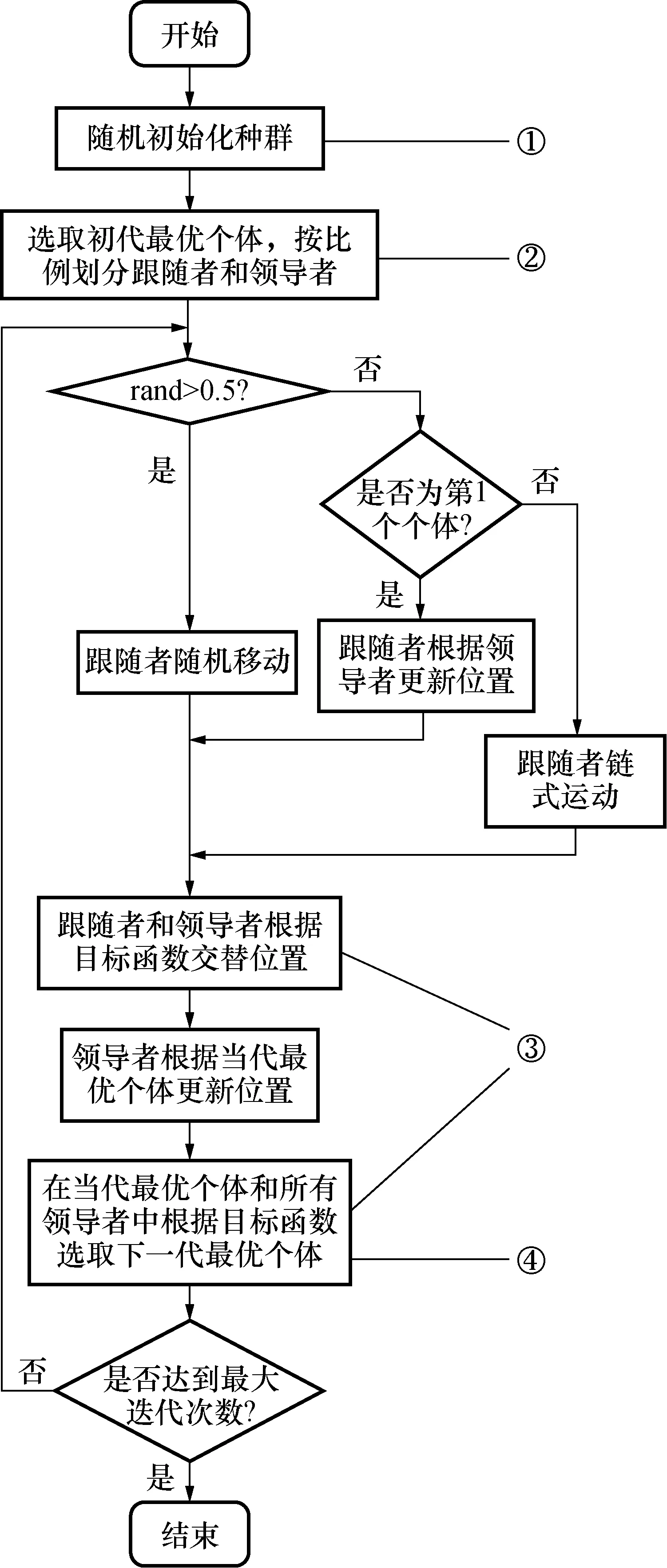
图2 标准COA流程图Fig.2 Standard COA flow chart

3.2 改进白骨顶鸡优化算法

本文在标准白骨顶鸡优化算法基础上做了图2所示的4处改进,提出了一种适用于ECT图像重建的改进白骨顶鸡优化算法。

① 使用佳点集生成种群位置代替随机生成种群位置

设计种群位置的原则是利用尽可能少的种群全面地表征整个空间所有潜在解的分布。倘若随机生成种群位置,则很难遍历解空间中的各种情况。为使种群位置能够在解空间上全面并且均匀地分布,本文采用佳点集方法生成种群位置。

佳点集原理为:设Gs是s维欧氏空间中的单位立方体,如果r∈Gs,形如:

1≤k≤n

(13)

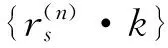
xi(j)=(ubj-lbj)·{rj(i)·k}+lbj

(14)

式中ubj和lbj表示第j维的上下界[13]。

图3(a)为佳点集在[0,1]内的种群个数为500,维度为1时生成的种群分布,图3(b)为Rand函数生成的种群分布。可以看出佳点集生成的种群在解空间上的分布更加均匀,设计出的群体具有更加丰富的多样性。

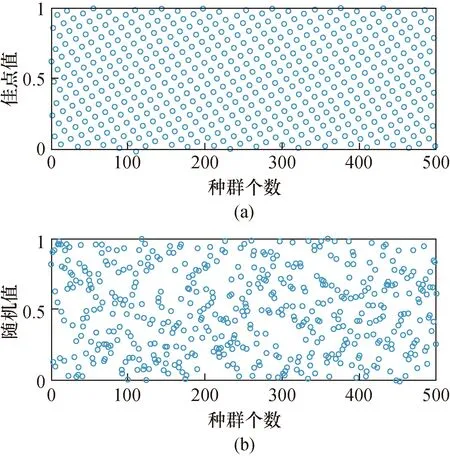
图3 分布图Fig.3 Distribution diagram

② 融合ART算法

标准COA中初代最优个体是在随机初始化的种群中根据优化目标函数选取产生的,但在未掌握相关问题在解空间的先验情况下,很难追踪解空间中的最优解,导致收敛时间增长。

在传统重建算法中,ART算法的重建质量较高。故将ART算法的成像结果作为初代最优个体,可快速稳定地跟踪介电常数的分布,使得重建算法的收敛性与准确性得到有效提高。

③ 目标函数

由式(4)可得,优化目标函数的一般选取原则为:将重建电容值与被测电容值之间的误差小,表达式为:

(15)

因为存在由于灵敏度矩阵S的近似性所带来的重建误差,所以当以式(15)为目标函数时,使算法可以收敛至全局最优,全局最优解与真实介电常数分布之间也会存在较大误差,即上式不对“软场”误差进行修正。

因此,本文提出一种考虑“软场”误差的目标函数。首先,定义式中ΔC1为电容测量值C与真实介电常数g*对应的电容值之差,即实际电容偏差,反映了“软场”效应造成的误差;定义式中ΔC2为电容测量值C与重建介电常数g对应的电容值之差,即重建电容偏差。

ΔC1=S·g*-C

(16)

ΔC2=S·g-C

(17)

将式(16)、式(17)分别取2-范数可得:

(18)

(19)

(20)

由于灵敏度矩阵S的列数远大于行数,求得的解不唯一,因此还需要添加适当的正则化项来指定解的特性[14]。

田鹏等在使用果蝇优化算法进行ECT图像重建时,为使重建图像质量更高,在目标函数中加入了标准Tikhonov正则化惩罚项[15]:

(21)

Tikhonov正则化将式(4)的逆问题转化为式(22)的最小化问题:

(22)

式中:α为正则化参数;L为正则化矩阵;g0为在先验信息中获得的估计解。

标准Tikhonov正则化将零向量作为估计解g0,会导致解过度光滑。本文将ART算法迭代10次的结果经过最优阈值处理后作为估计解g0。

经过改进后的目标函数为:

(23)

式中:L取为单位矩阵;α根据经验取为0.001。

④ 正余弦优化

在群体智能优化算法中,种群往往会陷入局部最优。为解决这个问题,在每次迭代选取最优个体的步骤中加入了正余弦优化算法。正余弦优化算法利用正弦函数和余弦函数的数学性质,是一种全局优化算法[16]。

正余弦算法对个体位置的更新方式为:

(24)

式中:Pos是种群位置;t是当前迭代次数;gBest是上一代最优解;r2是[0,2π]之间的一个随机数;r3是[0,2]之间的一个随机数,用于控制到最优解的距离;r4是[0,1]之间的一个随机数,作为转换概率;r1的计算公式为:

(25)

式中:t是当前迭代次数;tmax是最大迭代次数。

4 实验结果与分析

4.1 仿真实验

仿真实验模型采用12电极ECT系统,管道内径设置为62.5 mm,管道外半径为75 mm,屏蔽层半径85 mm。管内剖分12层,共1728个单元,管内成像区域剖分图如图4所示。

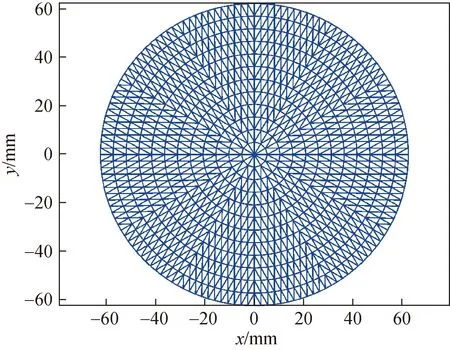
图4 管道剖分图Fig.4 Pipeline Division Drawing

设置单泡、两泡、三泡、环流和层流5种分布模型,模型中两相介质的介电常数分别为1和3。设置Coot种群数为1 000,领导者和跟随者各占20%和80%,迭代800次,重建结果如图5所示。为了验证提出算法的有效性,选择LBP算法、Landweber算法、ART算法的重建结果作为对照组,其中Landweber算法迭代100次,ART算法迭代10次。

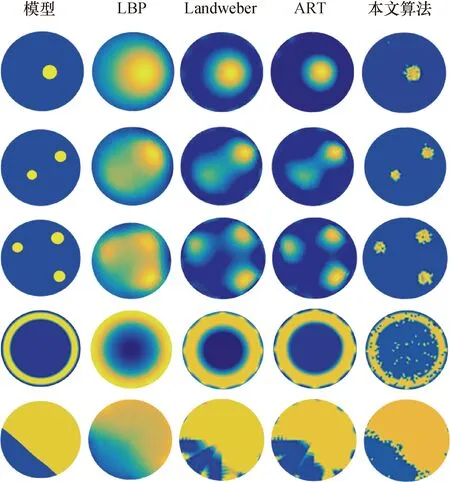
图5 仿真实验重建图像Fig.5 Simulation experiment reconstruction images

采用图像相对误差(ER)及相关系数(CC)作为重建图像定量评价标准,ER及CC的定义式为:

(26)

(27)

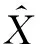
由以上两个公式可知,ER越小,CC越大,说明重建图像质量越好。仿真实验不同算法重建结果的图像相对误差和相关系数见表1。

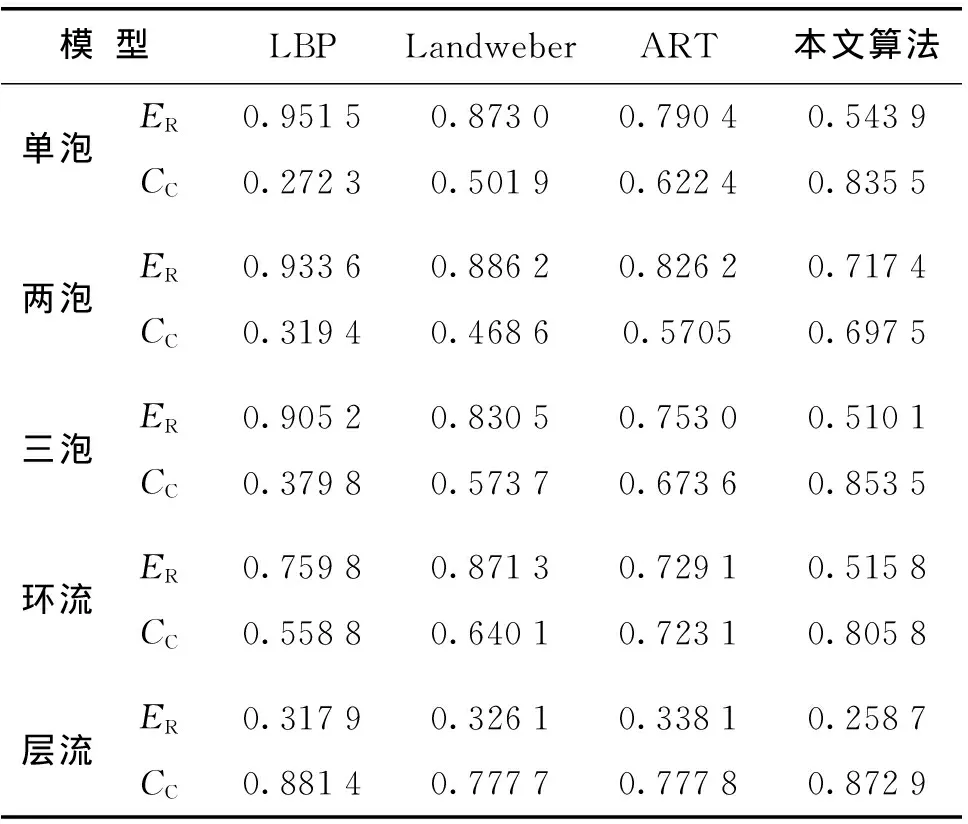
表1 图像相对误差和相关系数Tab.1 Image relative error and correlation coefficient

仿真结果表明,对单泡、两泡、三泡、环流模型而言,经典重建算法中ART算法的重建质量最好,Landeweber算法次之,LBP的重建质量最低,但都带有明显的伪影;但ART算法和Landweber算法对层流模型的重建结果中出现了较明显的形变,在ER和CC数值上可知,LBP算法的重建质量要优于ART算法和Landweber算法。相较于经典重建算法,改进的白骨顶鸡优化算法对5种模型的重建精度最高,重建介质的大小和位置最接近真实分布,重建图像的平均相对误差为0.509 2,平均相关系数为 0.813 1。

4.2 静态实验

采用华北电力大学测量实验室的数字化ECT测量系统进行静态实验,ECT系统如图6所示。

图6 数字化ECT系统Fig.6 Digital ECT system

静态实验采用12电极传感器,圆形有机玻璃管道内径为100 mm,空场和满场的标定分别使用空气和塑料颗粒。使用直径为15 mm的塑料棒模拟泡状模型,使用塑料颗粒模拟环流及层流模型。分别模拟了单泡、两泡、三泡、环流及层流5种气/油流型,并进行了模型图像重建,如图7所示。

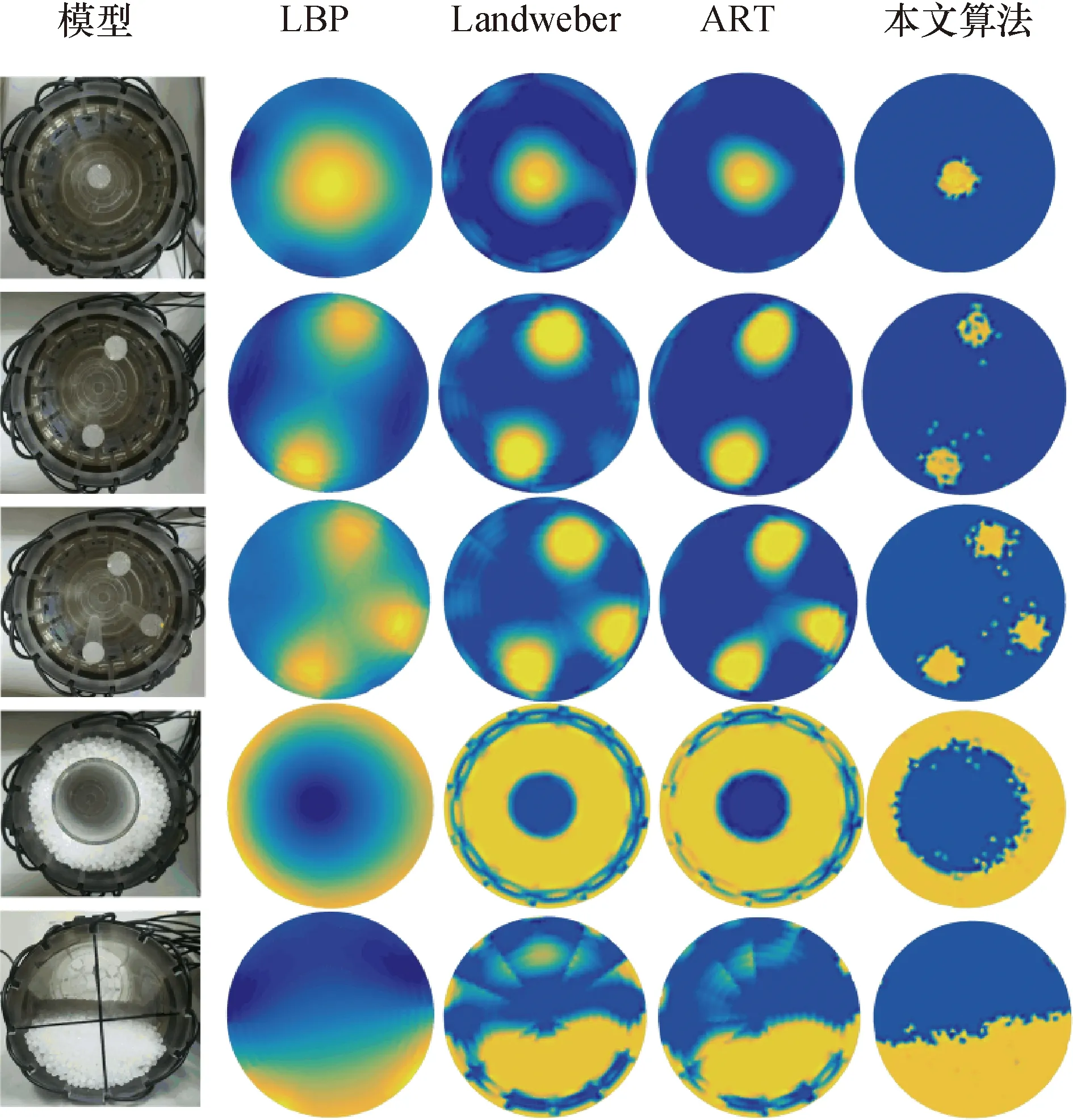
图7 静态实验重建图像Fig.7 Static experiment reconstruction images

由图7可见,改进白骨顶鸡优化算法的重建质量高于LBP算法、Landweber算法及ART算法,泡状模型重建图像伪影少,且能明显区分多泡模型中的每个泡,环流和层流模型的重建图像也更接近于静态实验真实的介质分布。

5 结 论

本文提出一种基于改进白骨顶鸡优化算法的ECT重建算法,使用佳点集方法和正余弦优化算法对标准COA进行优化,融合了传统ART重建算法,并根据ECT重建特点对目标函数进行了改进。在仿真实验和静态实验中与LBP算法、Landweber算法和ART算法进行了比较。结果表明,本文算法所得的重建图像质量有明显的改善。同时,本文算法也存在不足,如重建介质中存在“空点”或周围伴有“毛刺”,而且存在一定的随机性,这都是后续工作要解决的问题。