基于状态方程的Fx-RLS主动噪声控制方法

褚轶景, 赵越喆, 牛 锋, 陈明阳

(1.华南理工大学 亚热带建筑科学国家重点实验室，广东 广州 510641；2.中国计量科学研究院，北京 100029)

1 引 言

生活噪声、工业噪声、交通噪声是干扰人们生产生活、数据测量,乃至语言沟通的重要因素[1～4]。主动噪声控制(active noise control, ANC)是一种噪声控制的重要手段,广泛应用于低频噪声及振动消除[5～7]。一类广泛使用的自适应控制算法是滤波最小均方算法[7](filtered-x least mean squares, FxLMS)及其变体[8,9]。Fx算法存在次级通道(secondary path)建模问题,如跟踪路径变化、测量传声器[10,11]引起的建模误差等。在这种情况下,基于Fx算法的ANC系统由于滤波信号自相关矩阵不对称,将使消噪能力下降,甚至导致算法发散。

为了解决这个问题,通常采用正则化技术。其中一个较为成熟的应用是Leaky FxLMS算法[12]。该算法在自适应更新过程中,加入自相关矩阵对角加载(diagonal loading),从而增加算法鲁棒性。然而此类算法的收敛性分析表明正则化技术不能保证算法一定收敛。

另外,对于时变系统来说,固定的正则化因子往往不能取得最佳效果。文献[13]对FxLMS算法的鲁棒性进行了讨论,得到均值收敛充要条件,并提出一类利用正则化滤波器增加稳定性的FxLMS算法。但是该正则化滤波器的设计较复杂,在实际应用中不易实现。FxLMS算法的另一个问题是收敛缓慢,对于有色噪声等特征值分布不均匀的信号具有很高的灵敏度。虽然递归最小二乘算法(recursive least squares, RLS)[14]可以加快收敛,但跟踪速度及稳定性明显不如LMS类算法。文献[15]中提出的卡尔曼滤波(Kalman filter)克服了以上算法的不足,但复杂度较高。

综上所述,FxLMS算法对次级通道建模误差的鲁棒性较差,而基于卡尔曼滤波的ANC算法很难在计算量与跟踪速度上取得平衡。为了减小次级通道误差引起的降噪量下降,同时不大量增加算法复杂度,本文提出一种基于状态方程(state equation)的FxRLS(S-FxRLS)主动噪声控制算法。不同于传统RLS算法,改进方法创新点及特点如下:

改进方法将状态方程引入ANC系统用以描述控制器的先验统计特性,通过对控制器建模误差的估计确定先验统计特性,从而达到减小建模误差影响的作用。建模误差的估计对改进算法性能影响较大,本文提出一种近似估计方法,可以对建模误差进行有效估计。

另一方面,为了减小算法计算量,通过简化状态方程,使得控制器自适应估计在最小二乘意义上实现最佳递归估计。

由于基于RLS的ANC算法数学模型较复杂,目前对于这类算法理论分析方面的工作较少。为了定性研究提出算法性能,利用Price’s积分等数学工具,对算法在高斯输入加性噪声环境中的均值性能进行理论分析,得到均值意义上的收敛条件。

本文提出S-FxRLS算法后,对算法性能进行分析,最后通过计算机模拟,与传统Fx算法及其采用正则化技术的变体等算法进行比较。模拟结果表明:1) S-FxRLS算法较之传统FxLMS算法收敛速度加快了约60%;2) 次级通道建模误差导致传统FxLMS及正则化FxLMS算法出现发散现象时,本文提出的算法仍然保持较好的收敛特性。

2 ANC系统模型及S-FxRLS算法

基于Fx算法的ANC系统如图1所示。噪声源信号{x(n)}通过初级通道{p(n)}在某一区域产生噪声信号{d(n)}。另一方面,控制器{w(n)}通过自适应滤波生成扬声器(次级源)驱动信号,再经由扬声器到误差麦克风的次级通道{s(n)},产生噪声抵消信号{y(n)}。误差麦克风用于拾取n时刻信号残差{e(n)}。为了抵消误差麦克风接收到的噪声{d(n)},控制器{w(n)}旨在与次级通道{s(n)}级联后近似等于初级通道{-p(n)}。

图1 基于Fx自适应算法的ANC系统简图。Fig.1 Block diagram of an ANC system.

根据图1,待消除的噪声信号及控制器输出可分别表示为d(n)=p(n)*x(n)+η(n),y(n)=x(n)*w(n)*s(n),“*”表示卷积计算。误差信号则可表示为:

e(n)=d(n)+y(n)

(1)

假设声学路径和控制器变化缓慢,根据卷积交换定律可知,滤波信号xs(n)=x(n)*s(n)可以作为控制器的输入信号,从而滤波器输出信号可表示为y(n)=xs(n)*w(n)。下标s表示参考信号x(n)通过次级通道s(n)滤波。

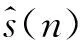
则抵消声信号可表示为:

(2)

为了增强控制算法的稳定性,采用如下状态方程描述控制器先验概率:

w(n+1)=w(n)+v(n)

(3)

式中:v(n)是L×1的高斯白噪声向量,自相关矩阵为Q(n)。由式(3)可知,控制器的先验概率分布满足均值为{w(n)}、方差为{P(n-1)+Q(n)}的正态分布

w(n+1)～N(w(n),P(n-1)+Q(n)),

式中:P(n-1)为先验估计方差,与控制器估计的准确度直接相关。

(4)

由控制器最大后验(MAP)估计:

w(n)=argmax[p(d(n)|w(n))p(w(n))]

(5)

可得S-FxRLS更新公式:

w(n+1)=w(n)-k(n)e(n)

(6)

(7)

后验方差更新由式(1)、式(6)及简单的数学推导可得后验估计方差的更新公式:

(8)

(9)

由算法的更新式(6)-式(9)可知,S-FxRLS算法复杂度在传统FxRLS算法的基础上增加了状态方程估计,增加的乘法数量为L,总计算量仍然与传统FxRLS算法相当,即o(L2)。

3 均值性能分析及收敛条件

算法的均值收敛特性研究是算法设计的重要方面,揭示参数估计与最优值之间的偏离,在保证算法收敛的同时为算法设计提供理论指导。为了使性能分析可行,本文做出以下假设:

假设3P(n)与输入信号相互独立。

3.1 均值分析

基于以上假设,同时假设算法收敛,则稳态更新公式表示为:

E[w(∞)]=E[w(∞)]-E[k(∞)e(∞)]

(10)

由此可知,E[k(∞)e(∞)]=0。将式(7)代入式(10)。由于P(∞)≠0,可得S-FxRLS算法的稳态解:

(11)

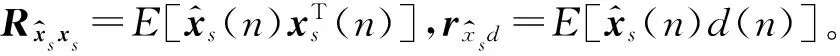
为了进一步分析算法均值特性,定义误差向量v=w∞-w(n)。由式(6)及假设3知:

E[v(n+1)]=E[v(n)]+P(n)L1

(12)

L1=-UΛDΛUTE[v(n)]

(13)

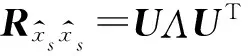
(2αβλi+1)-1dβ

将上述结果代入式(12),可得算法的均值插分方程:

E[v(n+1)]≅(I-P(n)UΛDΛUT)E[v(n)]

(14)

该方程代表算法的均值收敛速度。由式(14)可知,代表输入信号特征值的对角矩阵DΛ以及后验估计方差P(n)共同决定算法的收敛速度。与传统RLS算法类似,P(n)起到白噪化输入信号以及调整算法步长的作用,因此可令RLS类算法具有较快的收敛速度[17]。

3.2 均值收敛条件

将式(14)左右两边同时乘以UT可以得到:

E[V(n+1)]≅(I-Γw(n)ΛDΛ)E[V(n)]

(15)

式中:V(n)=UTv(n),Γw(n)=UTP(n)U。

为了使算法均值意义上收敛,式(15)右边小括号内矩阵的特征值必须小于1,即满足条件:

0<[Γw(n)]i,i<2/(λiIi(Λ))

(16)

另一方面,由式(8)以及广义Abelian积分同样可以得到Γw(n)的更新方程:

[Γw(n+1)]i,i≈[Γw(n)]i,i-λiIi(Λ)

(17)

式中:qi(n)是Q(n)的第i个元素。

(18)

式(18)可为算法设计提供理论依据,从而避免计算量巨大的试错法(try-and-error)选择用户参数。

4 仿真与实验结果

4.1 仿真结果

假设ANC系统置于较小的封闭空间(如车内),因此,初级通道阶数较短,设通道长度为12,次级通道长度为4,且具有估计偏差,估计偏差与次级通道内积的比值分别设为-6 dB和-3 dB。ANC控制器长度为10,噪声源为粉红噪声。FxLMS类算法步长设置为0.002。L2-FxLMS算法的正则化系数经过大量试错法调整,使得收敛曲线最优。FxRLS类算法的遗忘因子设置为0.99,以增加算法稳定性。S-FxRLS算法中,用来估计自相关矩阵方差的遗忘因子λe设为0.9。

各种算法收敛曲线见图2。从剩余均方误差(excess mean squares error, EMSE)曲线可以得到如下结论:

图2 EMSE对应迭代次数的收敛曲线Fig.2 The convergence curves of EMSE vs. iteration number

1) 传统FxLMS及FxRLS算法对次级通路估计非常敏感。当次级通路估计误差由-6 dB增加到-3 dB,FxLMS算法方差增加,而FxRLS算法出现发散的情况。

2) 如果正确选择正则化系数,L2-FxLMS算法可以通过增加diagonal loading有效降低控制器估计方差。

3) 在比较的算法中,S-FxRLS算法无论在低建模误差还是高建模误差,均具有最快的跟踪速度和最佳的鲁棒性,这得益于状态方程对控制器先验概率预测的有效性。

4.2 测量结果

ANC系统降噪量测量实验设置如图3所示。右侧白色扬声器发出频率为500 Hz的单频噪声,噪声信号由白色扬声器前方的参考传声器接收,作为参考信号传给控制器(由笔记本电脑发出指令,控制器实现)。控制器驱动左侧黑色扬声器发出抵消声,抵消声与误差传声器处接收到的噪声源信号相互抵消;同时,误差传声器接收到的残差信号也反馈给控制器。

图3 ANC系统降噪量测量实验设置图Fig.3 The settings of the measuring experiment of an ANC system.

ANC开启前与开启后误差信号功率谱密度(power spectral density, PSD)如图4所示。噪声源信号(蓝色虚线)经ANC控制后,500 Hz的噪声信号由-10 dB降低到-40 dB(红色实线),降噪量达到30 dB。这一过程中,次级通道由系统识别算法得到。得益于提出算法无偏估计的特性(具体见均值分析及式(11))以及对次级通道误差的鲁棒性,算法的降噪性能较稳定。

图4 ANC控制器开启前后,误差信号功率谱密度Fig.4 Power spectral density of the error signal collected by the error microphone when ANC is on and off

5 结 论

本文提出一种鲁棒ANC算法。通过算法性能理论分析证明该算法对于次级通道建模误差引起的算法发散问题有较好的抑制作用。同时,性能分析结果对于提出算法用户参数的选择具有指导作用。仿真及测量实验证明,基于状态方程的FxRLS(S-FxRLS)算法收敛速度比传统滤波最小均方(FxLMS)算法提高了约60%;稳定性方面,当采用正则化技术的鲁棒方法开始发散时,改进算法仍可收敛。最后实验测量证明,提出算法的单频降噪量可达30 dB。