能量天平悬挂线圈姿态调整方法研究

甘 伟, 曾 涛, 白 洋, 李正坤, 王 越

(1.中国计量大学 机电工程学院，浙江 杭州 310018；2.中国计量科学研究院，北京 100029)

1 引 言

2019年5月20日起,质量单位千克实现了基于普朗克常数的量子化定义[1,2]。目前,国际上将质量单位千克溯源至普朗克常数的主要方案有硅球法、功率天平法与能量天平法,其中能量天平法是我国自主提出的千克复现方案[3～6]。该方案基于通电线圈电磁力做功与线圈电磁能变化之间的能量平衡的原理,建立了普朗克常数h和砝码质量m的关系[7～9]。该能量平衡的建立是基于理想准直状态,即悬挂线圈受到的电磁力方向与砝码重力方向平行且电磁力作用线通过砝码质心。但在实际情况下,悬挂线圈总会与水平面之间存在夹角,使得电磁力在水平方向上存在力分量并在线位移上额外做功;此外,通电线圈所产生的电磁力作用点如果与砝码重力的作用点存在偏心距,使得电磁力在悬挂线圈上存在转矩并在角位移上额外做功,由此而引入的一系列误差被称为准直误差[10～12]。准直误差是制约能量天平相对测量不确定度优于2×10-8的主要因素之一,线圈的中心位置可以通过高精度位移平台调整,但姿态控制因存在强耦合作用而难以实现精密控制;并且当电机运动方向向下时,电机与电机提升机构之间接触不紧密,使得线圈上电前后姿态变化较大,影响姿态调整的准确性。抑制准直误差的关键是精密调整悬挂线圈姿态逼近至绝对水平,即在保证线圈中心位置不变的情况下,线圈与水平面间的夹角小于1 μrad。

对于悬挂线圈的姿态调整方法,各个开展功率天平项目的计量机构也进行过相关的研究。加拿大国家研究委员会(NRC)在其功率天平利用手动调整线圈上端3根支架的长度进而改变悬挂线圈姿态,虽然该结构简单可靠,但一次调整周期时间过长,控制精度过度依赖操作人员动作精细度,且无法在真空中对线圈姿态进行实时调整,存在真空-空气环境下的线圈姿态的不一致问题[13]。美国标准技术研究院(NIST)在其NIST-4通过增加三脚架配重从而改变悬挂系统重心来达到改变悬挂线圈姿态的目的,该方法虽然操作简单,但同样无法于真空环境中对线圈姿态进行实时调整,存在线圈准直状态漂移的问题[14]。能量天平是通过调节悬挂系统中3路压电陶瓷电机来改变3路连杆长度,进而带动悬挂线圈姿态发生变化[15],虽然实现了在真空中对线圈姿态的初步可调,但3路连杆的调整之间存在相互耦合,即在实际调整过程中,当调整单路连杆长度时,另外两路连杆长度同样会发生变化;同时为了保证线圈姿态调整的有效性,对于电机运动有着较强的约束,这种耦合及约束情况极大地影响了线圈水平姿态的调整效率。

本文基于能量天平电磁特性及力学特性,通过采集线圈在绝对水平附近的姿态控制实验数据,利用递推最小二乘法(RLS)得到线圈姿态离散状态空间模型[16]。在此基础上,基于能量天平悬挂系统初始位姿与寄生位移之间的数学模型[10],通过基于状态空间的模型预测控制(MPC)[17]将线圈姿态补偿逼近至绝对水平。该研究将提高悬挂线圈姿态调整效果,抑制准直状态不理想引入的测量不确定度,进而对降低能量天平装置的整体测量不确定度起到重要技术支撑。

2 悬挂线圈姿态系统

在能量天平中,悬挂线圈通过3根120°对称的碳素纤维连杆与上端的三角架连接,三角架与连杆之间通过压电陶瓷电机提升机构连接,整个悬挂线圈下端装有3路120°对称的角锥反射镜。3个角锥反射镜的轴线与相应的连杆轴线重合,3路激光干涉仪通过测量这3个角锥反射镜的位置来判断悬挂线圈姿态。通过调节上端3路压电陶瓷电机伸长量来改变连杆末端位置,进而改变悬挂线圈水平姿态,悬挂线圈姿态调整系统装置如图1所示。

图1 悬挂线圈姿态调整装置Fig.1 Suspension coil attitude adjustment device

能量天平的悬挂结构虽然能在真空环境下实现线圈姿态的初步实时调整,但对于悬挂线圈姿态精密调整,目前仍存在以下两方面问题。一方面,水平姿态以及3路连杆之间存在相互耦合,即当调整绕x轴的角度θx时,绕y轴的角度θy同样发生变化。这是因为当调整单路连杆位移时,另外两路连杆由于耦合同样产生位移,如图2所示,在控制1路连杆位移z1运动30 μm时,第2、3路连杆竖向位移z2、z3变化量可达15 μm,影响了线圈姿态调整准确性。另一方面,为了保证线圈姿态调整的有效性,即线圈姿态上电前后的一致性,对电机运动方向及线圈在竖直方向上的中心位置有着较强的约束。首先,3路电机最后一次运动方向须保持向上;其次,为了避免引入电机回程差,在调整过程中3路电机运动方向须保持不变;最后,在线圈中心位置不变的情况下,姿态调整至水平,即线圈绝对水平姿态唯一。

为了实现线圈姿态的精密控制,首先通过系统辨识在线圈姿态绝对水平附近建立离散状态空间模型;然后初步调整线圈至绝对水平位置下方,此时3路连杆位置在目标位置下方;最后,通过状态空间模型预测控制调整线圈姿态逼近至绝对水平,状态空间模型预测控制能够处理输入输出约束的同时实现对线圈姿态的解耦控制,从而达到准直误差补偿的目的。

3 悬挂线圈姿态控制模型

根据悬挂系统姿态调整装置可得悬挂线圈姿态调整坐标系如图3所示。图3中L1、L2、L3分别为3路激光干涉仪的测量位置。

图3 线圈姿态调整坐标示意图Fig.3 The coordinate diagram of coil attitude adjustment

令3路执行机构引入的杆长变化量分别为Δz1、Δz2、Δz3,根据坐标轴与悬挂线圈之间的几何关系,当悬挂线圈水平姿态的调整量为(Δθx, Δθy)时可得[12]:

(1)

(2)

式中r为悬挂线圈半径。

将式(1)、式(2)进一步写成绝对式矩阵形式:

(3)

式中:θx、θy为线圈绕x、y轴的角度,z1、z2、z3为3路连杆位置,由式(3)可知线圈姿态与3路连杆位置之间关系。

3.1 离散状态空间模型

悬挂线圈姿态调整系统输入为3路压电陶瓷电机伸长量,输出为线圈水平姿态,状态变量为3路连杆位置,可以通过3路激光干涉仪测得。将离散状态空间模型作为能量天平悬挂线圈姿态控制系统模型:

X(k+1)=AX(k)+BU(k)

(4)

Y(k)=CX(k)+DU(k)

(5)

式中:A,B∈R3×3,C∈R2×3,R3×3和R2×3分别表示3×3和2×3实数矩阵;Y(k)=[θxθy]T为悬挂线圈当前时刻水平姿态输出,悬挂线圈在竖直方向旋转角度相比于水平方向上旋转角度几乎可以忽略不计;X(k)=[z1(k)z2(k)z3(k)]T为当前3路连杆位置,U(k)为当前3路压电电机输入,U(k)=[u1(k)u2(k)u3(k)]T;X(k+1)为下一时刻3路连杆位置;式(5)中C、D由式(3)可知,此时系统未知参数为系数矩阵A、B。

3.2 模型参数辨识

系统辨识是获得复杂数学模型的主要方法,能量天平整体的复杂性使得对悬挂线圈姿态控制系统进行机理建模十分困难,且实际姿态调整过程中,系统具有强耦合、不确定性等特点,使用系统辨识法建模更为方便。设待辨识参数:

由递阶辨识[18]原理可知多输入多输出系统(MIMO)可以分解成多个子系统来进行单独辨识,将式展开后第j个子系统输出可表示为:

zj(k)=aj1z1(k-1)+aj2z2(k-1)

+aj3z3+bj1u1(k-1)

+bj2u2(k-1)+bj3u3(k-1)

(6)

式中:zj(k)为第j个连杆的当前时刻的绝对位置。

定义观测数据向量φ(k)和待辨识参数θj:

φ(k)=[z1(k-1)z2(k-1)z3(k-1)

u1(k)u2(k)u3(k)]

(7)

θj=[aj1aj2aj3bj1bj2bj3]T

(8)

得到式(6)的最小二乘辨识模型:

zj(k)=φ(k)θj

(9)

定义子系统的极小化误差准则函数:

(10)

式中:t为连杆位置的观测次数。令其导数为零,得其最小二乘估计为:

(11)

定义:

(12)

此时RLS可表示为:

(13)

利用RLS得到子系统的模型参数,然后通过新数据验证模型参数辨识的准确性。其中某个子系统的模型输出与实际输出如图4所示。

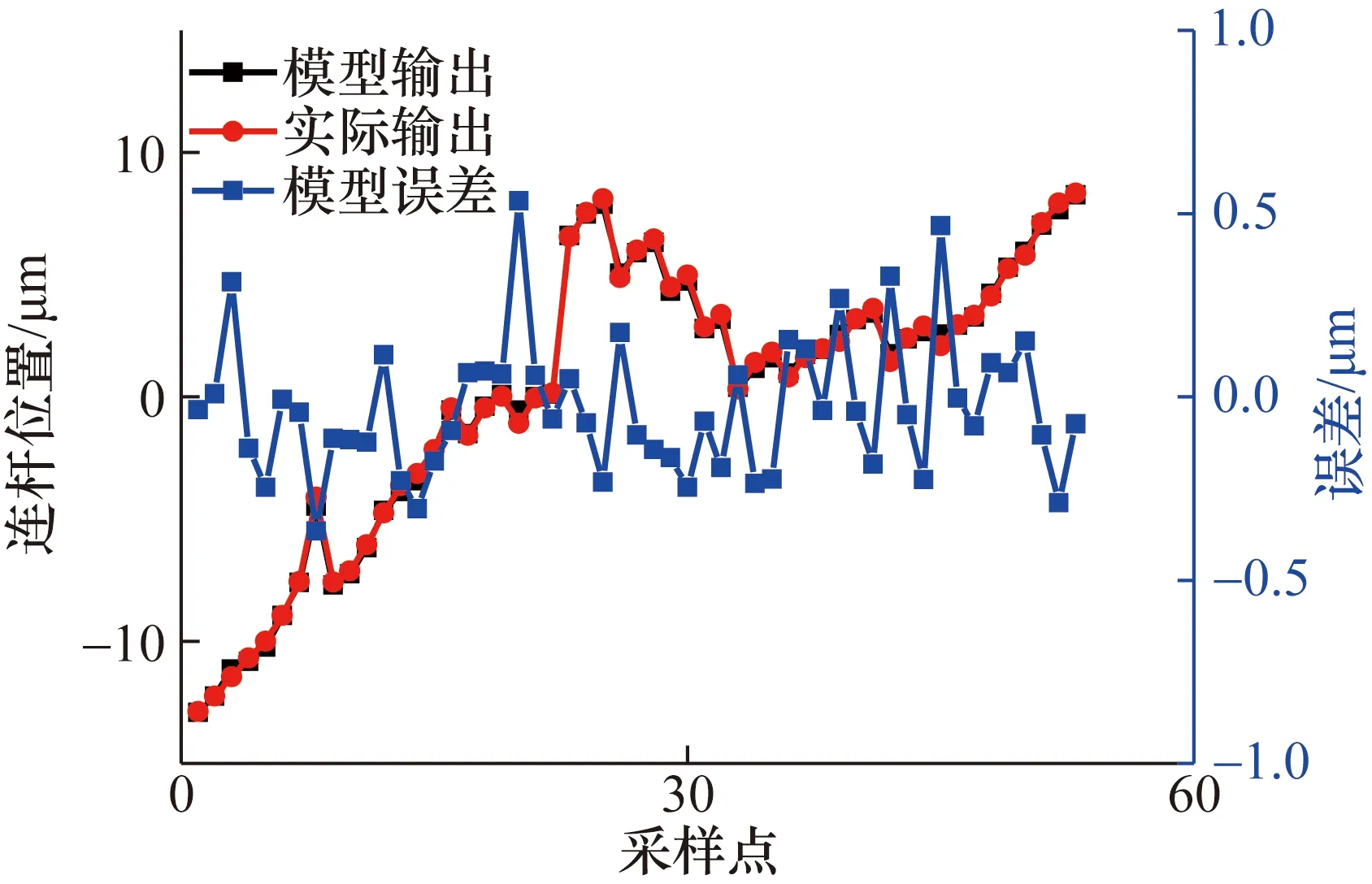
图4 子系统模型拟合图Fig.4 Subsystem model fitting diagram

由图4可知,子系统模型输出曲线与实际输出曲线基本重合,误差在±0.5 μm内,说明利用RLS得到的子系统模型准确。利用RLS将子系统逐个辨识完成后,原系统的未知参数也全部辨识完毕。当系统数学模型已知时,式(4)进一步化简后有

U(k)=B-1X(k+1)-B-1AX(k)

(14)

当已知当前连杆位置及目标连杆位置,控制量由式可知,就可以初步调整线圈至目标位置整体下方,再通过MPC调整姿态逼近至绝对水平。

3.3 状态空间模型预测控制

MPC是基于系统模型预测系统未来一段时间内系统状态,并通过二次规划确定在系统约束下的输入最优解,同时通过预测控制能够实现系统的解耦控制。悬挂线圈在姿态调整时先根据目标姿态求解目标3路连杆位置,再以3路连杆位置为实际输出,此时系统离散状态空间方程为:

Z(k+1)=AZ(k)+BU(k)

(15)

式中:Z(k)=C-1Y(k)为3路连杆当前时刻位置。定义Z(k|k)为k时刻预测的状态值;Z(k+N|k)为k时刻预测的未来第N个时刻的状态值;U(k|k)为k时刻预测的系统输入,U(k+N|k)为k时刻预测的未来第N个时刻的系统的输入值。则在未来N个时刻内有:

(16)

令:

则式(16)可表示为:

Zk=MZ(k)+DUk

(17)

式中:Zk∈R3(N+1)×1为3路连杆未来N个时刻下的输出序列;Uk∈R3N×1为未来N个时刻下的输入序列;M∈R3(N+1)×3,C∈R3(N+1)×3N为系数矩阵。

设最终目标输出参考值:

Zref=[zref1zref2zref3]T

(18)

定义极小化函数:

·Q(Z(k+i|k)-Zref)

+U(k+i|k)TRU(k+i|k)}

+(Z(k+N|k)-Zref)T

·F(Z(k+N|k)-Zref)

(19)

式中:Q=diag[q1q2q3]为误差权重矩阵,Q∈R3×3;R=diag[r1r2r3]为输入权重矩阵,R∈R3×3;F=diag[f1f2f3]为最终误差权重矩阵,F∈R3×3。

进一步化简,可得:

(20)

将式(17)代入式(20),化简可得:

(21)

进一步简化得到MPC的代价函数二次型标准形式为:

(22)

输入约束可表示为:

Umin≤U≤Umax

(23)

结合式与式可求出未来N个时刻下输入的最优值,然后将未来第1个时刻输入的最优值作用于系统,再根据当前时刻位置重新求解输入未来N个时刻的最优值,重复上述过程直至调整至目标姿态。综上可以将悬挂线圈姿态控制问题转化为带约束的优化求解问题。

4 仿真与测试结果分析

4.1 线圈姿态控制仿真实验

设辨识得到的系统模型参数为:

线圈姿态调整过程中,为了使得线圈姿态引入的准直误差最小化,线圈目标姿态为绝对水平即3路连杆的目标位置全为0 μm处。同时为了满足电机最终运动方向向上且控制过程中不存在反向的输入约束条件,在目标位置下方任意设定3路连杆初始位置分别为-4、-8、-15 μm。使用状态空间模型预测控制对系统进行控制,3路连杆位置和水平姿态变化仿真结果如图5所示。

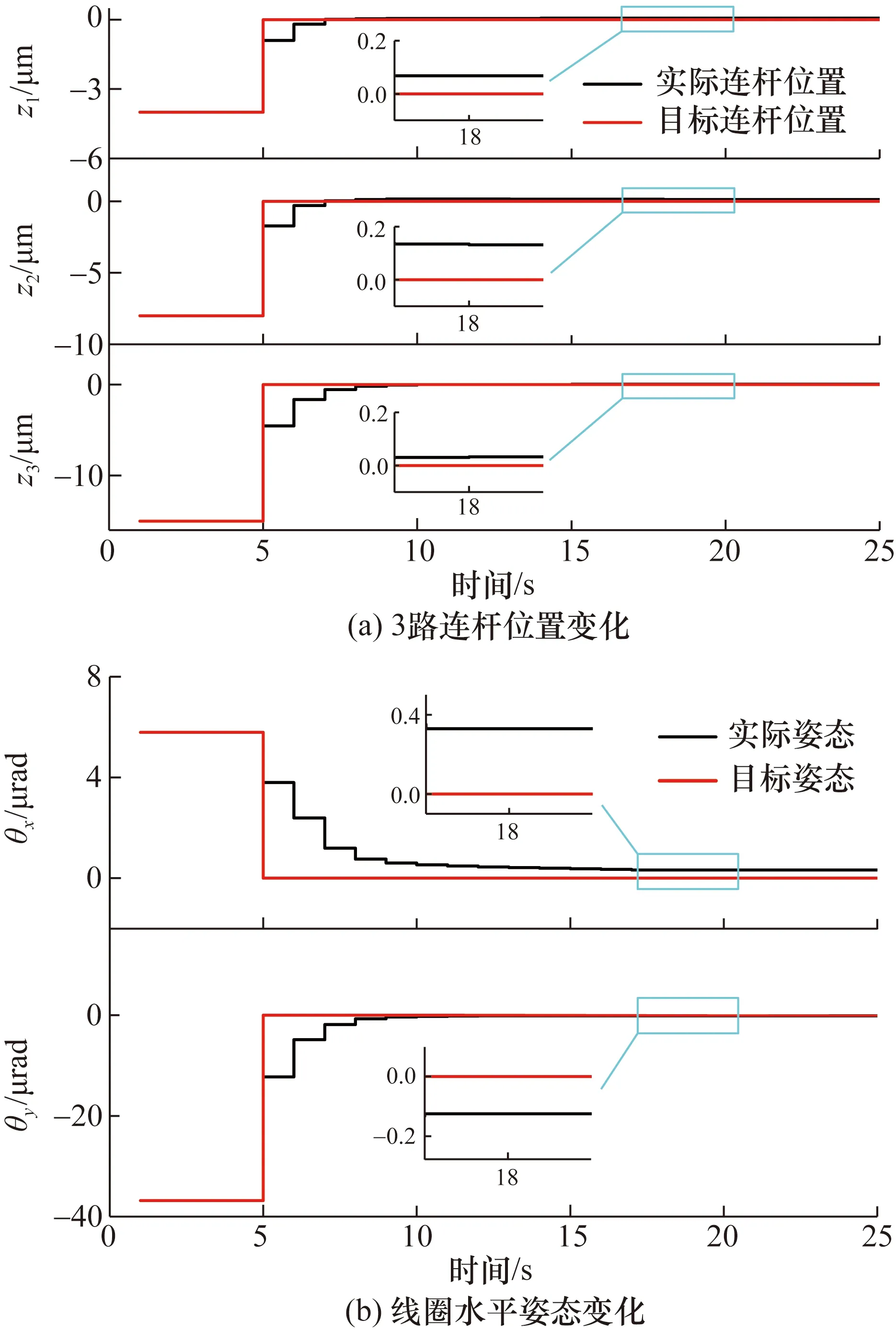
图5 杆位置变化和线圈水平姿态变化Fig.5 Changes in rod position and coil horizontal attitude

由图5可以看出,3路连杆位置z1、z2、z3及线圈水平姿态θx、θy快速变化至稳定,系统的稳定性强,3路连杆位置控制误差小于0.2 μm,水平姿态控制误差小于0.4 μrad。通过MPC可以快速调整线圈姿态逼近至理想状态,从而能够很好地抑制由于线圈姿态产生的准直误差。

4.2 实验结果分析

为了证实状态空间模型预测控制的有效性,将该方法运用到实际线圈姿态控制过程中。在目标位置下方任意选定初始3路连杆位置分别为-3.36、-7.46、-11.57 μm,调整线圈姿态至绝对水平即3路连杆目标位置全为0 μm处。3路连杆位置及线圈水平姿态变化实验数据如图6所示。

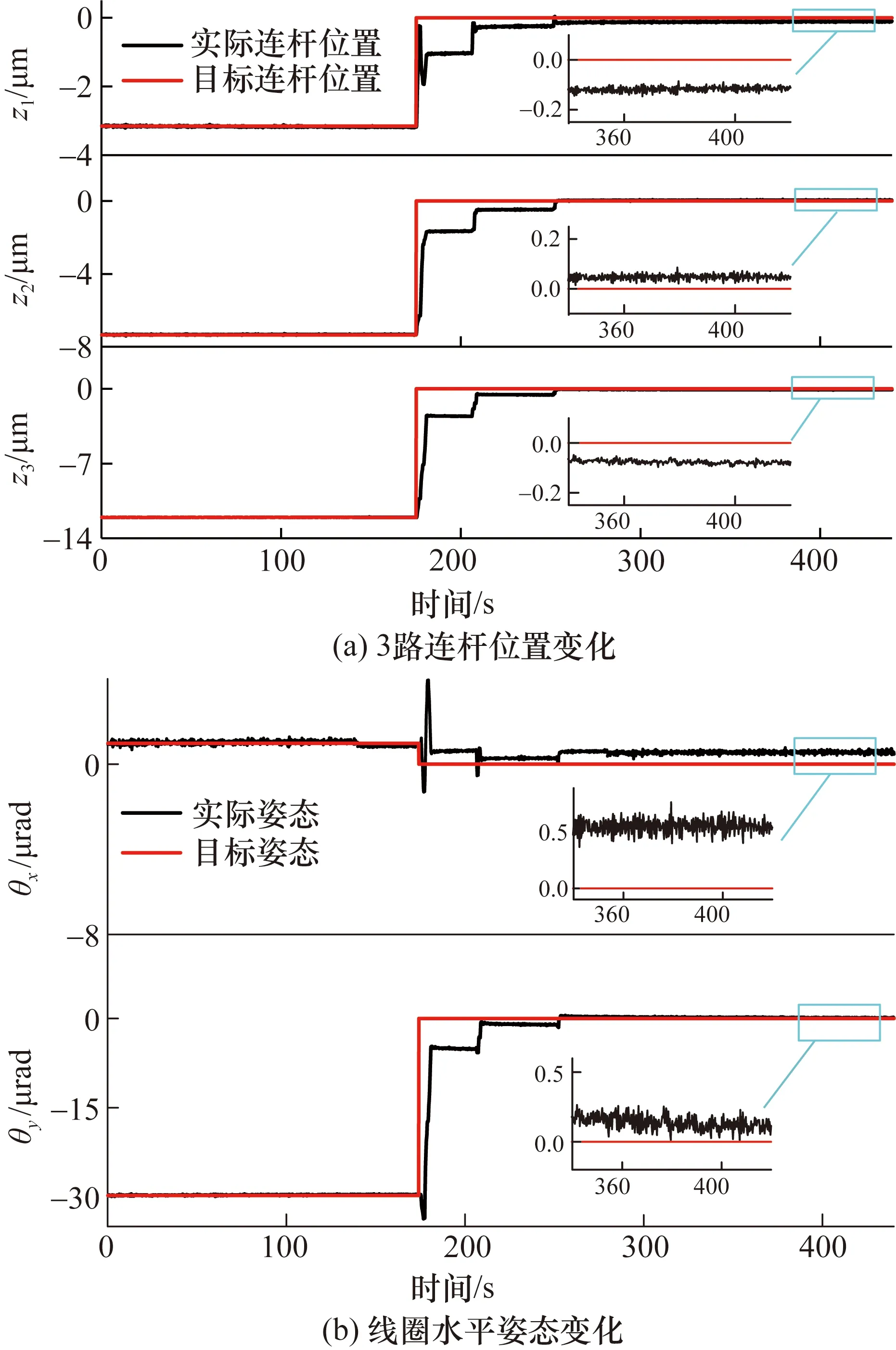
图6 杆位置变化和线圈水平姿态变化Fig.6 Changes in rod position and coil horizontal attitude

由图6可知, MPC能够快速有效调整3路连杆及线圈姿态逼近至目标状态,系统输出中心位置基本稳定,3路连杆位置控制误差小于0.2 μm,水平姿态控制误差小于0.8 μrad,证明了MPC运用在能量天平悬挂线圈姿态调整上的有效性。选定10个不同的线圈初始姿态,重复调整线圈至绝对水平姿态,最终3路连杆位置控制误差e1、e2、e3及水平姿态控制误差ex、ey如表1所示。

表1 连杆位置与线圈姿态控制误差Tab.1 Link positon and coil attitude control errors

由表1的数据可知:3路连杆位置控制误差均小于0.22 μm,线圈水平姿态控制误差均小于0.98 μrad,3路连杆位置在0.25 μm、线圈姿态在1 μrad的误差内能够逼近至绝对水平,满足线圈姿态控制要求。实验表明,MPC能够很好地调整能量天平悬挂线圈姿态逼近至绝对水平,抑制由于线圈姿态引入的准直误差。

5 结 论

能量天平中悬挂线圈姿态的初始姿态不理想是准直误差的主要来源,对线圈姿态进行精密的控制是抑制准直误差的关键。针对线圈姿态控制存在强耦合无法精确调整的问题,本文基于能量天平力学特性,通过系统辨识在线圈姿态绝对水平位置附近建立相关的离散状态空间模型,并利用状态空间模型预测控制调整线圈姿态逼近至绝对水平。最终3路连杆控制准确度优于0.25 μm,姿态控制准确度优于1 μrad,能够满足线圈姿态控制要求,为准直误差地抑制提供了重要的技术支持。