经济政策不确定性与中国股市波动率预测——在GARCH-MIDAS模型下的实证研究

王刚贞,宋大伟

(安徽财经大学 金融学院,安徽 蚌埠 233030)

一、引言

“守住不发生系统性金融风险的底线”是我国建设现代化经济体系和高质量经济发展的必然要求。为防止金融风险的发生,政府部门必然会出台一系列的财政、货币和其他的经济政策,这些经济政策的频繁出台或变动无疑会对我国金融市场产生一定的影响,而股票市场作为金融市场的重要组成部分,频繁的政策出台或变动会加剧股票市场的波动。然而,股票市场价格的波动在资产定价、投资组合选择、套期保值和风险度量中具有至关重要的作用,因此研究经济政策的变化对股票市场的影响有着非常重要的理论和现实意义。

研究经济政策的变化如何对股票市场产生影响的关键是具有不确定性的经济政策如何度量。基于以往大量的研究,学者们往往用不同的经济指标作为经济不确定性的代理变量。然而,Baker等[1]基于新闻报道和相关指标用文本分析法构建了经济政策不确定性指数(EPU),该指数能够及时地、连续地反映经济政策的变化从而克服使用某一类指标来代表不确定性经济政策变化的局限性。EPU 一经出现便受到学者们的关注,有很多学者将其用到不同的领域进行了相关研究并取得丰硕的成果。尽管对经济政策不确定性的研究已在各个领域取得丰硕成果,但目前还鲜有文献同时考虑中国经济政策不确定性(AEPU)、美国经济政策不确定性(GEPU)和全球经济政策不确定指数(GEPU)对上证综合指数波动率的影响,而且以往对EPU 的研究主要集中在与EPU 具有相同频率的数据上,使用同频数据进行实验并不能将数据中包含的重要信息充分反映出来,进而使得实证结果与现实情况有较大偏离。与以往研究不同,本文将研究视角集中在CEPU、AEPU 和GEPU 变化对上证综合指数波动率的影响上,并采用混频数据(5分钟高频数据、日度数据和月度数据)模型进行实证研究。

以往对波动率的研究大多采用GARCH 族和CARR 模型,这两类模型对波动率建模时只是考虑到高频数据或日内价格变化,未考虑混频数据对股票市场的影响,Ghysels等[2]提出混频抽样(MIDAS)回归模型,Engle等[3]将GARCH 模型和MIDAS模型结合,构造了广义自回归条件异方差混频抽样(GARCH-MIDAS)模型来考察长期和短期成分对股票市场波动的预测能力。研究结果发现,将低频成分加入到GARCH-MIDAS模型中能显著提升模型的预测精度。在GARCH-MIDAS研究的领域内,郑挺国和尚玉皇[4]在国内率先基于宏观基本面构建GARCHMIDS模型,并运用该模型对本国股市日内波动率进行估计,研究结果表明多因子GARCH-MIDAS模型可以改进基准GARCH 模型的预测效果,并且充当长期成分的宏观经济变量对股市波动具有正向影响。Yu[10]、雷立坤[11]、余江[12]、Wang[14]等将EPU 作为长期低频成分运用到GARCH-MIDAS模型来研究EPU 对中国股票市场的影响,实验结果均表明加入EPU 的GARCH-MIDAS 模型比没有加入 EPU 的GARCH 族模型在波动率预测精度上表现更好,并且EPU 能够很好地解释我国股市波动的长期成分。

基于对上述过程的理解,本文与以往研究不同之处如下:1)以CEPU、AEPU 和GEPU 为长期低频变量的代理变量,以上证综合指数(SSEC)的5分钟高频数据和日内波动率作为短期高频的代理变量来从不同角度考察各个国家EPU 指数对中国股市波动的影响;2)将多个不同的EPU指数加入到GARCH-MIDAS 模型之中,并与基准GARCH 模型进行对比;3)为增强模型的稳健性,本文采取向前h=1、h=5和h=10预测,同时采用4种损失函数和Diebold和Mariano的检验来考察各类模型预测能力的差异。

二、GARCH-MIDAS模型

(一)基于已实现GARCH-MIDAS 模型的构建

对股票市场波动率建模最常使用的模型之一是GARCH 模型,但GARCH 模型所用数据往往是同频数据,未能将不同频率的数据所包含的丰富信息对波动率的影响反映出来。为研究CEPU、AEPU 和GEPU 对中国股市波动率的影响,本研究采用Engle和Ghysels[8]在2013提出的GARCH-MIDAS 模型来研究EPU 对股票市场的影响。GARCH-MIDAS的描述如式(1):

式(1)中,ri,t是第t个月中的第i天的对数收益率,μ是ri,t的无条件均值,即E(ri-1,t)=μ,εi,t|Φi-1,t～N(0,1),即εi,t在Φi-1,t的条件下服从标准正态分布,而Φi-1,t是第t个月中第i-1天的信息集合。gi,t度量的是短期高频波动成分,它服从GARCH (1,1)过程,具体如式(2):

式(2)中,α和β分别代表ARCH 和GARCH 过程,同时α,β＞0且α+β＜1,保证了gi,t的非负性和平稳性。E(gi,t)=1,保证了Et-1[(ri,t-μ)2]=τtEt-1(gi,t)=τt,τt表示长期低频波动的成分,它被Engle等[8]通过使用MIDAS滤波滑动平滑RV 得到,具体如式(3):

式(3)中,m为常数项,θ是RVt对长期波动τt的影响系数。θ为正,说明RVt和τt之间是正相关的关系;反之,则两者间存在负相关关系。K是MIDAS模型中RVt的最大滞后阶数,而φk(ω1,ω2)是一个Beta型权重函数,其中ω1,ω2是φk(ω1,ω2)方程中的参数,函数的具体形式如式(4):

为保证滞后项权重呈现衰减形式(滞后期越小,对当前影响越大)和模型计算简便,本研究采用Borup和Jakobsen(2019)、Xie和Wu[4,15]等的做法,将ω1=ω2=1。由此得到简化后的Beta权重函数具体形式如式(5)(6):

式中,RVt是已实现波动率,其是由第t天的第i个5分钟交易数据收益率的平方加总得到。通过以上对GARCH-MIDAS 模型的介绍,可以发现ri,t的条件方差被分解成短期成分gi,t 和长期成分τt,gi,t 服从GARCH(1,1)过程,即方程(2)所示,而τt代表的长期成分可以用方程(3)来刻画。与其他多成分波动模型相比,GARCH-MIDAS模型的参数设置很简约。

(二)基于经济政策不确定性构建已实现GARCH-MIDAS模型

接下来用中美经济政策不确定性(低频变量)构建GARCH-MIDAS 模型,该模型的具体形式如式(7):

当θ1=θ2=0时,GARCH-MIDAS就转化为GARCH 模型,Xt-k表示经济政策不确定性指数(CEPU、AEPU 和GEPU),用极大似然估计来对方程(1)至(7)进行参数估计,具体函数形式如式(8):

其中,Θ=(m,α,β,θ1,ω1,θ2,ω2)'是模型中的参数组成的向量,ℓ(R;Θ)部分对数似然回报率,模型中参数的最大似然估计值可以通过计算最大似然函数得到如式(9):

三、实验结果

(一)数据

本文研究的数据样本为上证综合指数(SSEC)和Baker等编制的中国经济不确定指数(CEPU)、美国经济政策不确定性指数(AEPU)和全球经济政策不确定性指数(GEPU)。其中,上证综合指数为5分钟高频数据和日交易数据,样本的时间跨度为2000年1月4日到2020年12月31日,一共5 086个交易日,数据来源于Wind数据库。而CEPU、AEPU 和GEPU 为月度数据,样本区间为2005年1月到2020年12月,共192个月,数据来源于政策不确定网站(www.policyuncertainty.com)。本文将样本分为两部分:第一部分样本区间为2000年1月4日到2019年5月30日,共4 698个样本进行样本内参数估计;第二部分样本区间为2019 年5 月31 日到2020年12 月31 日,共388 个数据进行样本外预测。

(二)描述性统计量

从表1数据中SSEC的对数收益率r和价格极差R 的描述性统计量可以看出,对数收益率r的偏度小于0,而峰度大于3,说明收益率r呈现向左偏的同时存在尖峰厚尾的现象。从图1可以看出,对数收益率表现出波动率聚集现象,从图2可以看到CEPU、AEPU 和GEPU 在2008 年后波动加剧,从2008 年金融危机爆发后,CEPU、AEPU 和GEPU 均呈现出逐渐上升的趋势,在2015年中国股市爆发股灾后,防范金融风险和避免股灾地再次发生,政府部门近年来出台一系列经济政策以防止股票市场过度波动,一系列政策的出台或变动使得CEPU 在近几年的波动变得更加剧烈。

图1 SSEC收益率的图

图2 EPU变化趋势图

图3 GARCH 模型样本内拟合和样本外预测

图4 GARCH-MIDAS(RV)样本内拟合,样本外预测,长期波动和短期波动

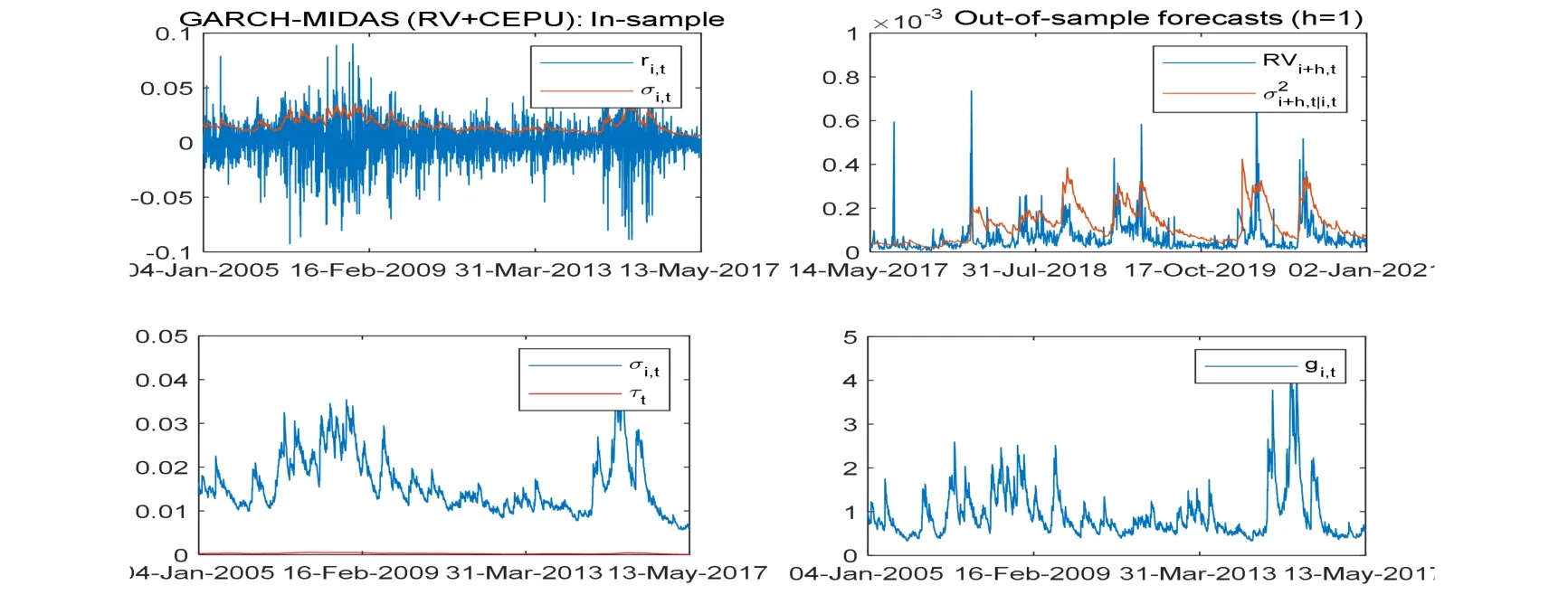
图5 GARCH-MIDAS(RV+CEPU)样本内拟合,样本外预测,长期波动和短期波动

图6 GARCH-MIDAS(RV+AEPU)样本内拟合,样本外预测,长期波动和短期波动

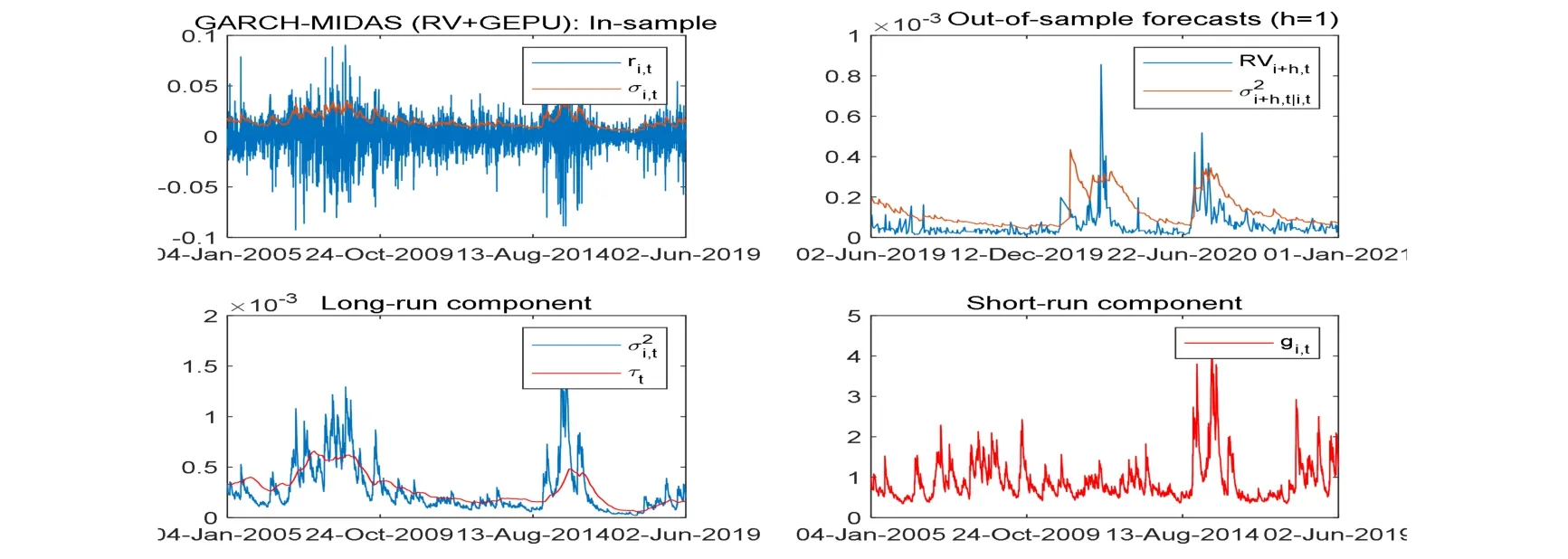
图7 GARCH-MIDAS(RV+GEPU)样本内拟合,样本外预测,长期波动和短期波动

表1 描述性统计量

(三)参数估计

本文使用GARCH 类模型对中国股市进行波动率预测,其中对模型参数估计使用的数据包含两类:一类是股票市场收益率数据,是日度数据,时间区间从2000年1月4日到2019年5月30日,共4 698个日度股票市场收益率数据;另一类是经济政策不确定性指数,是月度数据,时间区间是从2005年1月4日到2019年5月30日,共164个数据。这两类数据用来进行参数估计。模型的样本外预测使用的数据主要是2019年5月31日后的数据,用这些数据对中国股票市场收益率进行预测,并通过检验来证明模型的预测能力,验证构建全新的GARCH-MIDAS模型以及引入经济政策不确定性能够改进模型的波动率预测效果。

从表2中的参数估计结果,能够观察到几个显著的结论:β＞0,同时所有的β接近于1,说明上证综合指数波动率具有高度持续性,值得注意的是 GARCH-MIDAS 类模型的β值都比GARCH 模型的β值小,可能的原因是GARCH模型中的β只能捕获短期波动而GARCHMIDAS类模型能够捕获分量的长期成分。同时发现,α,β＞0且α+β＜1,GARCH 模型是平稳的。MIDAS模型的月度已实现波动率的斜率参数θ1大于0,而EPU 的斜率参数向量θ2在所有模型中明显小于0,说明经济政策的不确定会明显影响股票市场波动。在表2中,我们还可以观察到GARCH 和GARCH-MIDAS模型的Loglik值比加入EPU 指数GARCH-MIDAS模型的Log-lik值要小,说明加入EPU 指数能提升模型样本内的拟合能力。

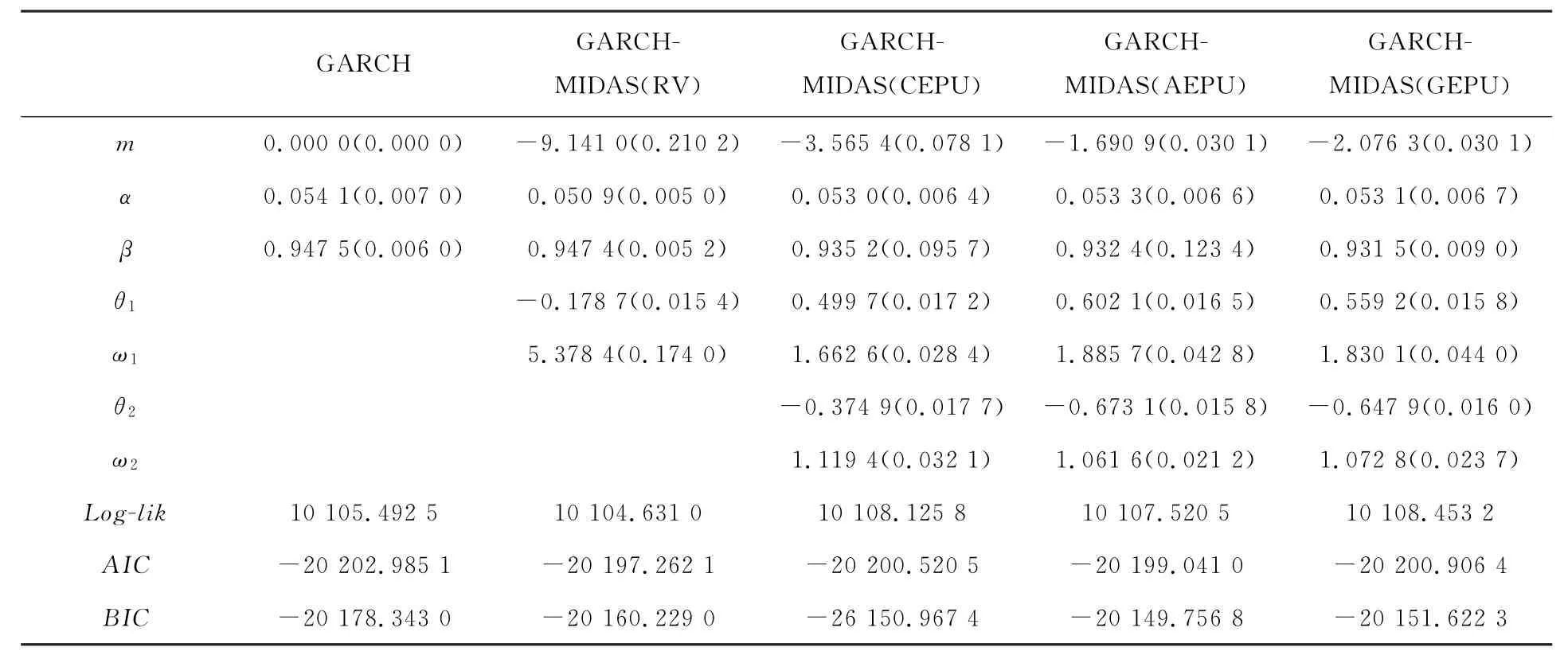
表2 GARCH 类模型参数估计结果

(四)样本外结果

1.模型预测能力的比较

与样本内拟合相比,模型的样本外预测能力对市场参与者更重要,因为投资者更关心模型预测未来的能力,而不是分析过去的能力。本研究将数据样本分为两个部分,即样本内和样本外。样本内的时间跨度为2000年1月4日到2019年5月30日,共4 698个样本来进行样本内参数估计;样本外采用向前h步的滚动时间窗口进行波动率预测,样本外的时间区间为2019年5月31日到2020年12月31日,共388个数据来进行样本外预测。为观察经济政策不确定性对中国股票市场波动的影响,本文采用CEPU、AEPU 和GEPU 纳入GARCH-MIDAS模型来进行样本外预测。Hasen和Lunde[12]指出,用某一个损失函数来进行样本外预测,可能得到的样本外预测结果并不稳健。本文选取4个损失函数来评判模型预测性能的优劣,4 种损失函数分别为MAE(mean absolute error)、MAPE(mean absolute percentage error)、MSE(mean squared error)和QLIKE(Quasi-likelihood)。损失函数的具体表达式如下所示:

方程式(10)～(13)中,MV是对波动率的测度,可以是RV或RNG,h(m)表示模型预测的波动率,T是样本数量,m表示参与预测的模型。损失函数值越小,则反映的模型预测精度越高,预测结果如表3所示。

表3 模型样本外预测评价结果(h =1)

表4 模型样本外预测评价结果(h =5)

表3～表5的结果显示,考虑长期波动率成分的GARCH-MIDAS模型在样本外预测性能要比仅考虑短期波动率成分的GARCH 要好,在GARCH-MIDAS模型中加入经济政策不确定性指数的样本外预测能力比没有考虑的经济政策不确定指数的GARCH-MIDAS模型的预测性能要好。从加入经济政策不确定性指数的GARCHMIDAS 模型中可以发现,加入 CEPU 的GARCH-MIDAS 模型的损失函数最小,加入GEPU 次之,最后,是加入AEPU 的GARCHMIADS模型,结果说明中国股票市场不仅受到本国政策不确定的影响,而且还会受到外国经济政策的影响。

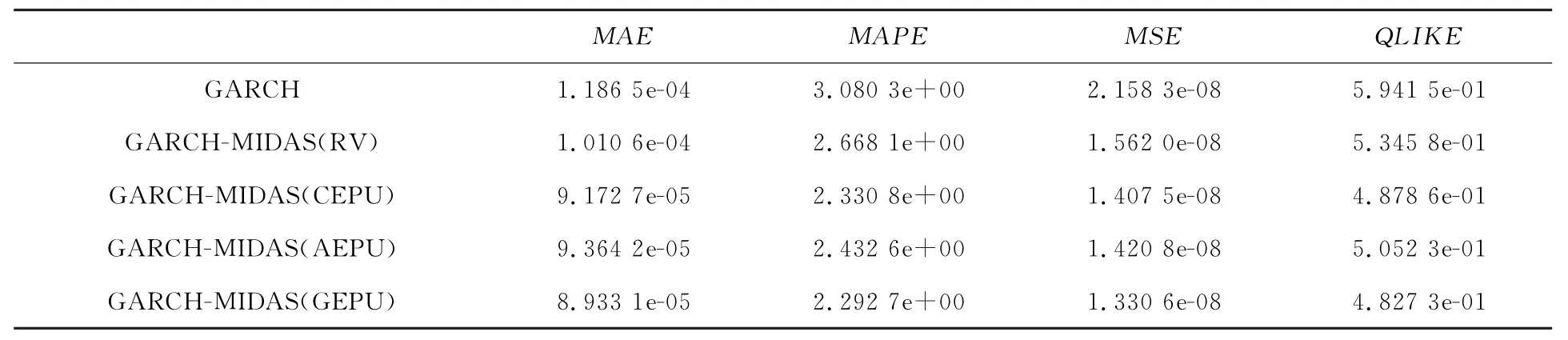
表5 模型样本外预测评价结果(h =10)

2.DM 检验

从损失函数可以了解模型预测性能的优劣,但是无法判别模型在统计意义上是否显著,而DM 检验则可以解决这个问题,DM 适用于两个或多个模型间预测能力的比较。假设模型的真实值为{yt;t=1,…,T},模型中两个预测值分别为和,两个模型的预测误差为{εi,t;i=1,2}。其中εi,t的表达式如下式:

假设与预测i相关的损失是预测误差εi,t的函数,并用{g(εi,t),i=1,2}来表示损失函数。g(εi,t)要满足3个条件,损失函数非负;损失函数在两个不存在误差时,函数的取值为0;损失函数随着误差的增加而变大。

dt是损失函数的一阶差分函数,当且仅当损失函数对所有的t具有的期望值为0时,即E(dt)=和具有相同的预测精度。因此我们构造原假设和备择假设。

原假设H0:E(dt)=0 ∀t

备择假设H1:E(dt)≠0

原假设是两个预测模型具有相同的预测精度,备择假设说明两者不具有相关的预测精度。DM 统计量的构造可以通过以下方式进行:

γd(τ)是dt的第τ阶自协方差,γd(τ)的具体函数方程如下:

构造DM 统计量:

(0)与fd(0)是一致估计量,当H0成立时,DM统计量服从N(0,1),用MAE、MAPE、MSE 和QLIKE作为DM 检验的基准函数,选择GARCH模型作为对照函数进行DM 检验,具体的检验结果如表6～表8所示。

表6 各模型的DM 检验结果(h=1)

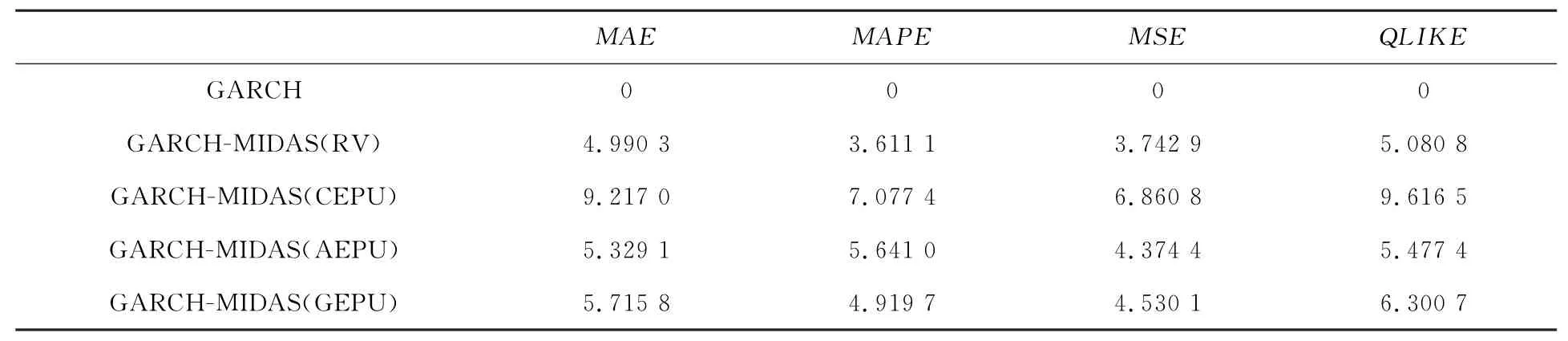
表7 各模型地DM 检验结果(h=5)

表8 各模型地DM 检验结果(h=10)

由方程(19)可知DM 统计量服从标准正太分布,通过查阅标准正太分布的分位数表,可知在1%、5%和10%的显著性水平下,对应统计量的值分别为2.57、1.96和1.64。由表6 ～表8可知,加入经济政策不确定性指数的GARCH-MIDAS 模型和未加入经济政策不确定性指数的GARCH-MIDAS模型,两者都在1%的显著性水平下显著,但加入经济政策不确定性指数与没有加入经济政策不确定性指数模型相比,前者可以提升模型的预测能力。从向前1步预测、向前5步预测以及向前10步预测的DM 检验结果进行比较可以发现,向前预测步骤越长,模型预测能力会变的越弱,即DM 统计量会变得越小。从h=1、h=5和h=10的DM 检验结果发现,CEPU 的DM 统计量最大,GEPU 其次,最小值是AEPU。这说明对中国股票市场波动产生影响的主要来源是本国经济政策的变化,由于我国金融市场在逐步对外开放,中国股票市场的波动可能不会因为某一个国家政策的变化而产生剧烈波动,因此GEPU 对中国股票市场的影响要比AEPU 对中国股票市场的影响大。

四、结 论

准确预测股票市场波动率在资产定价、投资组合选择、套期保值和风险度量中有着至关重要的作用。本文在GARCH 模型的基础上加入MIDAS模型,分别结合CEPU、AEPU 和GEPU 指数的GARCH-MIADS模型与GARCH 进行对比来研究经济政策的变化能否提升对中国股票波动率的预测能力。采用上证综合指数数据,数据时间区间为2000 年1 月4 日到2020 年12 月31日,共5 086 个数据;CPEU、AEPU 和GEPU 为月度数据,样本区间为2005年1月到2020年12月,共192个月。研究结果发现:在样本内参数估计结果表明,GARCH-MIDAS 模型比GARCH模型能更好地拟合我国股市的波动状况,同时加入EPU 指数能提升模型的预测性能,GEPU 对中国股市长期波动的解释作用最强,CEPU 次之,最小的是AEPU;样本外预测DM 检验表明,加入EPU 指数的GARCH-MIDAS 模型比没有加入EPU 指数的GARCH 和GARCH-MIDAS模型能显著提升模型预测能力,从h=1、h=5 和h=10的DM 检验结果发现,CEPU 的DM 统计量最大,GEPU 其次,最小值是AEPU,说明中国股票市场长期波动受到政策变化的冲击主要来自于本国经济政策的变化。

本文的研究结论有利于股票市场监管当局和经济政策制定者正确认识经济政策变化对中国股市的影响。政府部门应避免经济政策的频繁变动,保持经济政策出台的连续性和一致性,为有效避免政策时常变动引发投资者的错误预期从而导致金融市场剧烈波动,在制定政策前广泛听取各界人士的专业性意见,合理引导投资者的预期。金融监管部门一方面要完善对EPU 的检测和调控体系,合理有效的检测体系是防范风险的“警报器”,在风险发生前有效的检测系统能及时警示风险的到来,进而制定合理的应对措施;另一方面要将外国经济政策变化对本国金融市场的影响考虑进来,并将其纳入本国系统性风险监控体系之中,本国金融市场正逐步对外开放,对外开放虽有诸多好处,但也对我国金融市场抗风险能力提出挑战,有关部门要防止外国经济政策变化对本国金融市场产生剧烈震荡。有鉴于此,监管部门需建立更加完善的多元检测系统。