脉冲星时与原子时联合时间尺度建立初步研究

朱幸芝，童明雷，赵成仕

脉冲星时与原子时联合时间尺度建立初步研究

朱幸芝，童明雷，赵成仕

（中国科学院 国家授时中心，西安 710600）

原子时具有较高的短期稳定度，基于毫秒脉冲星自转建立的脉冲星时具有较高的长期稳定度，两者融合可构建长短稳优势兼具的时间尺度。本文通过经典加权平均算法，初步构建一个脉冲星与原子钟融合的联合时间尺度（composite time scale，CT）。基于国际权度局（BIPM）公布的TA(NTSC)-TAI原子时数据，并选取国际脉冲星计时阵（IPTA）公布的计时精度最高的4颗脉冲星，通过并列加权法和分类加权法这两种组合方式得到CT。结果表明并列加权法得到的CT相对于各脉冲星时在10年以内的稳定度改善明显，4～10年内稳定度与稳定度较高的脉冲星J0437-4715接近。分类加权法得到的CT对比并列加权的稳定度结果在采样区间两极优势明显，0.26年达到5.1×10-15，16.8年达到1.0×10-15，其中4颗星相比2颗星得到的CT于5.2年后稳定度有显著提高，且分类加权法得到的CT相对于TAI偏差更小，时间尺度更平稳。综上说明原子钟组的短稳特性可以对脉冲星钟组的短期噪声进行抑制，同时脉冲星时可提高联合时间尺度CT的长期稳定度。

时间尺度；脉冲星时；原子时；稳定度

0 引言

时间基准是科技发展的基础，也是国防建设的战略保障，安全、可靠、自主、可控是基本要求。目前国际上时间计量和服务主要依赖于国际原子时（TAI）[1]，该时间基准是由原子钟导出的原子时，作为一种积分时间尺度，因其具有误差累积的特性而影响长期稳定性。地方原子时TA（）由守时实验室根据钟组数据加权计算得到，TA（）具有优秀的短期稳定度（一般≤×10-15/30 d），但其长期稳定度会随着时间推移而降低。原子钟受制造技术和环境影响，可能因原子钟故障或环境（电源）保障失效，从而造成原子时中断，故原子时的长期稳定性和可靠性不理想。现代原子钟，如美国国家航空航天局（NASA）的深空原子钟（DSAC）的频率稳定度可以达到10-15/d[2]，然而对于独立原子时来说，随机频率噪声（RWFN）最终导致时钟频率偏离，在几年甚至几十年的平均时间内保持高精度守时仍然是一个挑战。

脉冲星是高速自转的中子星，其中毫秒脉冲星自转极其稳定，是自然界最稳定的“天然钟”[3]，基于毫秒脉冲星自转建立的时间尺度称为脉冲星时，其显著特点是其长期稳定度高。2012年，G. Hobbs等[4]利用Parkes天文台脉冲星计时阵（PTTA）中19颗毫秒脉冲星约17年观测资料，以国际原子时TAI为参考建立综合脉冲星时，精度在15年尺度上与TT（BIPM）相当。基于脉冲星自转建立的脉冲星时是与原子时物理机制完全不同的时间尺度，脉冲星计时的长期累积数据证明，脉冲星时比原子时具有更高的长期频率稳定度。利用脉冲星计时数据可改进原子时的长期稳定性，同时结合原子钟的短期稳定性优势和脉冲星的长期可用性、高稳定性，可构建一个新的联合时间尺度。以提高时间尺度的长、短期稳定性为目标，既可以有效利用原子钟组的短稳特性对脉冲星钟组的短期噪声进行抑制，也可以保持脉冲星组本身的优良长期稳定度。

在联合时间尺度建立研究方面，针对全铯钟时间尺度短期波动较大，而长稳性能较好；全氢钟时间尺度短期性能良好，但3个月以上的漂移较大的现实问题，2019年，姜萌等[5]提出了基于Vondrak-Cepek滤波的氢-铯融合原子时间尺度算法，有效利用氢钟的优良短期稳定度对铯原子钟时间尺度进行了平滑，有效地减弱了噪声对时间尺度的影响。同年，Chen Poting等[6]从滤波角度研究利用Hadamard方差评估脉冲星驾驭原子钟的优点和不足，该方法将原子钟和脉冲星信号的噪声统计信息进行融合，由于使用稳态卡尔曼增益，得到经脉冲星驾驭的原子钟短期稳定度降低，但长期稳定度显著提高。2020年，赵书红等[7]将基准频标与守时型频标联合，采用卡尔曼滤波算法计算氢-铯钟、光-铯钟联合时间尺度，其中光钟比铯喷泉钟在精度和稳定性方面高出一个量级以上，产生了一个更加准确、稳定的纸面时间尺度，并设计了基准频标与守时型频标联合的频率驾驭算法。

目前国内在时间尺度方面研究主要以综合脉冲星时[8]和综合原子时及其时频应用为主，关于脉冲星时与原子时联合时间尺度方面研究稀缺，为得到高稳定度性能的纸面时间标准，本文结合脉冲星时和原子时的天然稳定度优势，利用经典加权法并基于实测数据对脉冲星时和原子时进行融合，得到一种比综合原子时具有更高长期稳定度的联合时间尺度，提高时间基准的稳定性和可靠性。

1 经典加权平均算法

为了削弱脉冲星时中各独立噪声源的影响，从而得到一种更加稳定的脉冲星时间尺度，1996年 G. Petit等人[9]提出了利用经典加权平均算法建立综合脉冲星时，设计该算法的出发点是希望获得最好的长期稳定度。毫秒脉冲星长期稳定度高，而原子钟具有较高的短期稳定度，二者结合守时有利于优势互补[10]，D. N. Matsakis[11]曾尝试利用PSR1855+09的计时观测改进美国海军天文台（USNO）原子时TA（A.1），经过TT-PT1855与TA（PTB）-TA（A.1）的简单算术平均得到一种新的时间尺度，结果表明，它比TA（PTB）-TA（A.1）具有更高的频率稳定度。

经典加权算法可以对不同时间尺度的数据进行加权处理，即将多个钟差数据组合成综合钟差，从而得到联合时间尺度。其优势在于：经典加权算法对异常值和噪声有较好的抵抗能力，能够在一定程度上消除由于某个钟出现偏差或故障而导致的错误；可以适用于多个钟的数据组合，并可以根据需要对不同钟的权重进行调整；能够将多个钟差数据组合成一个更加精确和稳定的综合钟差，从而提高综合时间尺度的精度。目前已经被广泛应用于综合时间尺度的计算，经过多年的实践验证，其性能表现良好，是目前应用最为广泛的算法之一。

经典加权算法是所有时间尺度综合算法的基础，其原理即对每一个参与钟的时间尺度在整个观测时间间隔内取单一权重进行加权综合，建立脉冲星时与原子时联合时间尺度，经典加权法的基本公式[12]如下：

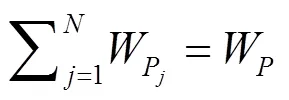
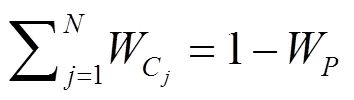
2 联合时间尺度建立过程及结果分析

建立脉冲星与原子时联合的时间尺度，即将脉冲星和原子钟都用于自由时间尺度的计算。首先需要筛选计时精度高、红噪声较小、计时跨度长的毫秒脉冲星，同时获取中国科学院国家授时中心原子钟钟差数据，根据其稳定度性能选取参与综合计算的原子钟。由于脉冲星时和原子时计时方式不同，在综合之前必须根据各自数据特点进行以下处理：① 脉冲星计时数据处理：利用Tempo2软件对脉冲星计时观测数据进行基本参数拟合，得到计时残差数据。② 原子钟比对数据处理：受环境和运行环境影响，原子钟可能出现跳变、数据缺失和数据异常等情况，需要对跳变和异常值进行频率和相位检测并校正，保证其在建立CT之前是连续时间序列，并去除原子时频率漂移。③ 参考时标统一：脉冲星计时观测与原子时测量比对的参考时间不同，为保证参与综合的各时间尺度的时间参考一致，综合前需要将各自的时间参考统一到相同的参考时标，如：TAI或TT（BIPM）。④ 数据等间隔处理：脉冲星计时观测采样区间不均匀，以计时误差为权重，采用30天间隔加权移动平均法对脉冲星计时残差数据的时间间隔进行均匀化，可以充分考虑各时间点对应的计时误差，避免数据失真，并且不影响一年以上稳定度；同时对原子时截取公共时间区间，以插值方式进行等间隔处理，以和脉冲星时对齐时间刻度。具体数据处理流程如图1所示。

图1 脉冲星时和原子时综合前数据处理流程

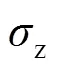
为得到高稳定度性能的联合时间尺度，必须尽量选择高稳定度的脉冲星和原子钟参与综合。对脉冲星时而言，参照综合脉冲星时建立准则，应选择计时精度高、具有长时间跨度、数据点密集并连续、且红噪声较低的脉冲星，更利于建立高稳定度联合时间尺度，并评估长期稳定度性能。本研究选取国际脉冲星定时阵列（International Pulsar Timing Array，IPTA）于2019年最新发布的计时精度最高脉冲星[16]，经脉冲星计时软件Tempo2处理得到相对于TAI的计时残差。TA（NTSC）是基于国家授时中心守时钟组的原子钟数据采用类ALGOS算法加权平均得到，具有很好的稳定度性能，可作为地方原子时的典型代表，本研究获取国家授时中心守时实验室提供、由国际权度局（International Bureau of Metrology，BIPM）公布的TA（NTSC）-TAI作为输入原子时，取公共时间跨度MJD：50 814～56 978，按前述要求对脉冲星时和原子时完成数据预处理。以下为基于经典加权法的几种计算方案及其对应结果分析。

2.1 并列加权法

由于脉冲星短期内受计时观测白噪声影响较大，且目前脉冲星计时观测TOA测量精度远低于原子钟之间的时间比对精度，导致得到的脉冲星时的短期稳定度低，但长期稳定度高是脉冲星时的典型优势。原子时短期稳定度高，但长期稳定度随时间推移而有所下降，故两类时间尺度在同时间跨度对应的稳定度差异较大，必须根据脉冲星时和原子时稳定度特性设置对应权重。本方案选取计时精度最高的两颗脉冲星J1713+0747、J0437-4715与原子时TA（NTSC）-TAI参与综合，共同计时跨度约16.8年，脉冲星时和原子时具体稳定度分布如图2所示。并列加权法即将各时间尺度视为同类型时间尺度进行加权综 合，以各参与时钟的频率稳定度的平方倒数为权重综合得到联合时间尺度。为减少权重本身带来的误差，脉冲星时采用/2（约8.4年）处稳定度，原子时采用最低短稳（约1年）值，以最大限度提高联合时间尺度CT的长期稳定度为宗旨，同时尽量不损失短稳。经J1713+0747、J0437-4715两脉冲星时（PT-TAI，图中简称PT）和原子时TA（NTSC）-TAI（简称AT）联合得到的CT结果如图2所示。结果表明，CT相对于单脉冲星在10年以内的稳定度改善明显，相对原子时而言，CT在4～10年内稳定度与稳定度较高的脉冲星时J0437-4715接近，在跨度为8.4年时达到2.0×10-15，说明并列组合下的经典加权法有效改善了联合时间尺度CT的短稳，且脉冲星组本身的优良长期稳定度可以提高CT的长稳性能，使之保持了脉冲星组本身的优良长期稳定度。

图2 两颗脉冲星时、原子时和并列加权法得到的CT稳定度

2.2 分类加权法

由单颗毫秒脉冲星定义的脉冲星时间PT受多种噪声源影响，如参考原子时误差、行星历表的不确定性、星际介质不稳定性、引力波、以及脉冲星自身的不稳定性等，除原子时本身的噪声外，可认为其他的噪声源对不同的脉冲星是独立的，通过建立综合脉冲星时可削弱各独立噪声源的影响，提高稳定度性能，尤其是长期稳定度。此外，为进一步削弱脉冲星时短稳对CT短稳的影响，考虑到脉冲星的测量结果不受相位和频率漂移的影响，但它们受到非常大的短期噪声影响而导致短稳差，通过傅里叶低通滤波方式可以有效去除白噪声并提高综合脉冲星时的短稳。根据综合脉冲星时的功率谱密度曲线确定最佳低通滤波起始频率值，取低通滤波截止频率为145天分之一，即去除截止频率值以上的高频噪声。由两颗星通过经典加权法构成的综合脉冲星时（EPT）在低通滤波前后的稳定度如图3所示。结果说明，该方法可明显提高EPT在1年内的稳定度。

图3 滤波前后的综合脉冲星时EPT和原子时的稳定度

分类加权法即将各单脉冲星时综合后得到综合脉冲星时，对其低通滤波后再与原子时作为两类时间尺度进行双尺度加权平均得到CT。为保证融合时间尺度的长期稳定度，根据EPT和原子时定度曲线分布，取各自于/2（约8.4年）处稳定度平方倒数为权重进行加权综合，得到的CT稳定度结果如图4所示。结果显示，分类加权比并列加权得到的CT在5.6年以上的稳定度更具有优势，EPT经低通滤波后与原子时综合，可显著提高CT一年以内的稳定度。分类加权法对于需要在计时跨度两端稳定度性能要求更高的应用场景更合适。图5展示了两种组合方法得到的CT钟差随时间分布图，其中分类加权得到的CT时间尺度的标准差比并列加权提高了0.56×10-7s，说明分类加权得到的联合时间尺度CT相对于TAI偏差更小，时间尺度更平稳。

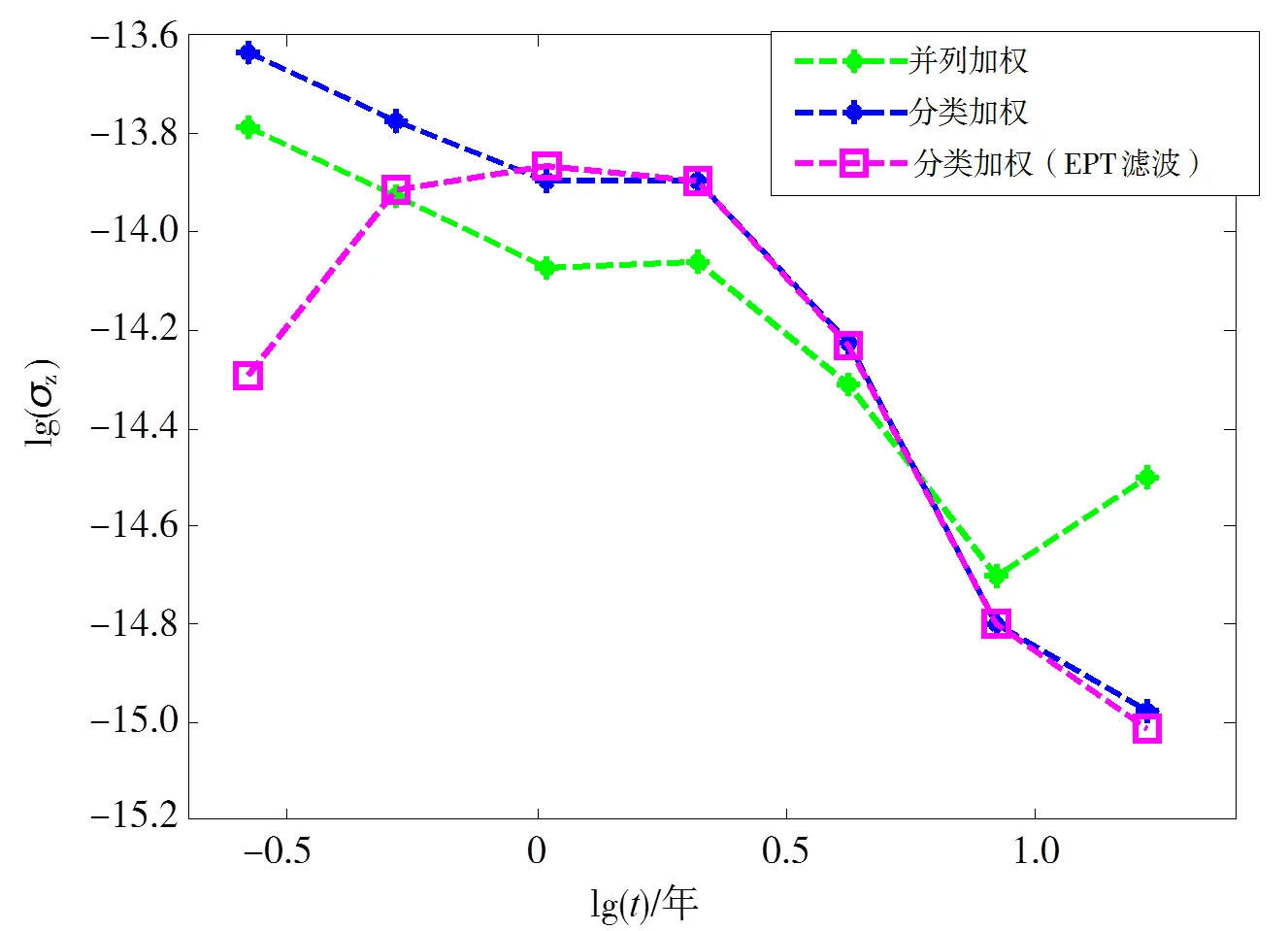
图4 利用2颗星基于分类加权和并列加权两种组合得到的CT稳定度

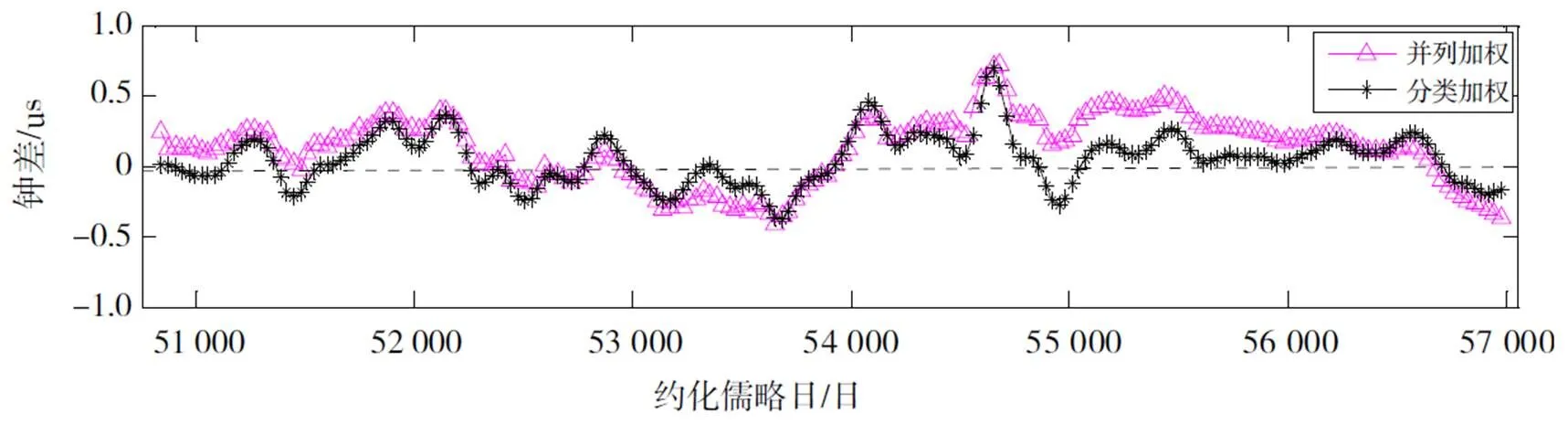
图5 两种组合方式得到的CT时间尺度随时间分布图

2.3 多星与原子时综合

由于参与综合的钟性能直接影响CT的稳定度性能，为进一步提高CT稳定度性能，并体现多颗星综合对CT结果的影响，取IPTA最新发布的J1713+0747，J0437-4715，J1909-3744，J1744-1134四颗脉冲星，均具有计时精度高、计时跨度长和红噪声相对小的特点，原子时只截取TA（NTSC）相对于TAI自主保持的钟差数据段，以显示真实的地方原子时频率偏移，以上所有参与钟的公共跨度约为10.8年。计算综合脉冲星时采用残差RMS（root mean square）的平方倒数作为各星的权重，这对于红噪声小的脉冲星更利于得到高稳定度性能的EPT，同时用上述两种组合方式计算得到CT，取权方式与2颗星情况相同，得到对应的CT稳定度如图6所示。结果显示基于4颗星的分类加权比并列加权在5.4年附近的稳定度略差，其余时间跨度内都要更高，相比2颗星的计算结果，在约5.2年以后的稳定度明显提高。

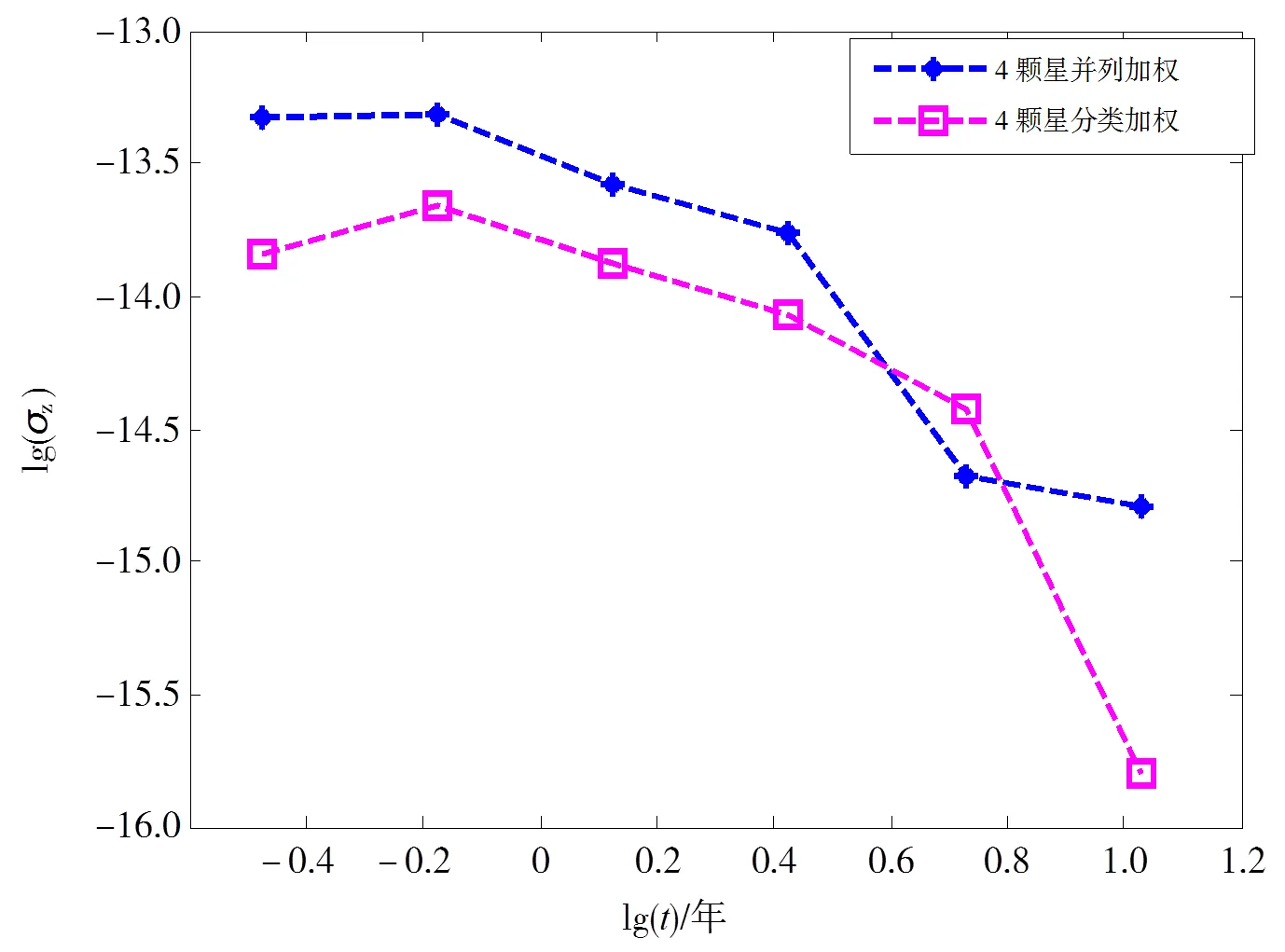
图6 利用4颗脉冲星基于两种组合方式得到的CT稳定度

3 结论

本研究通过经典加权平均算法，基于BIPM公布的TA（NTSC）-TAI最新原子时数据，并选取国际脉冲星计时阵（IPTA）公布的计时精度最高的4颗脉冲星，通过并列加权和分类加权这两种组合方式，初步构建一个脉冲星时与原子时融合的联合时间尺度。通过两种组合方式计算发现，并列加权组合得到的CT相对于单脉冲星在10年以内的稳定度改善明显。分类加权得到的CT比并列加权在采样区间两极的稳定度有明显提高，在多星参与综合后，CT的长稳更具优势。基于脉冲星时和原子时建立复合时间尺度，既可以通过原子钟组的短稳特性对脉冲星钟组的短期噪声进行抑制，也可以利用脉冲星组本身的优良长期稳定度提高综合时间尺度的长期稳定度。

一个时间尺度的长期稳定度是它作为时间标准的基本特性之一，经典加权方法可以更好发挥脉冲星时的长稳优势，但在时间尺度综合时只能对单个钟赋予一个单一权重，选择性地使某一种稳定度达到最好，故该方法有一定的局限性。针对不同类型的时间尺度融合，没有普遍适应的算法，只有根据具体应用目的来衡量方法的有效性。作为所有时间尺度综合方案的基础算法，本研究为后续方法的改进提供了参考和比对基础。

多颗脉冲星时与TA（NTSC）融合得到的CT，可改善我国地方原子时的长期稳定度性能。CT可作为特殊时期原子时的备份，作为一种“纸面时”，无需与国际原子时系统进行溯源或比对，依据CT可建立一种独立于国际标准时间（UTC）的时间保持体系。随着毫秒脉冲星计时观测规模化和规范化发展，以及原子时频率稳定度的飞速发展，两者融合后的综合时间尺度性能会进一步提高，未来有望以CT为频率驾驭参考建立UTC（NTSC），使其准确度和长期稳定度都进一步提高，为我国时间基准实现长时间跨度下独立自主守时迈出重要一步。

[1] 董绍武, 王燕平, 武文俊, 等. 国际原子时及NTSC守时工作进展[J]. 时间频率学报, 2018, 41(2): 73-79.

[2] TJOELKER R L, PRESTAGE J D, BURT E A, et al. Mercury ion clock for a NASA technology demonstration mission[J]. IEEE Transactions Ultrasonic Ferroelectrics Frequency Control, 2016, 63(7): 1034-1043.

[3] GUINOT B, PETIT G. Atomic time and the rotation of pulsars[J]. Astronomy & Astrophysics, 1991, 248: 292-296.

[4] HOBBS G, COLES W, MANCHESTER R N, et al. Development of a pulsar-based time scale[J]. Monthly Notices of the Royal Astronomical Society, 2012, 427(4): 2780-2787.

[5] 姜萌, 董绍武, 武文俊, 等. 基于Vondark-Cepek滤波的氢铯时间尺度融合方法研究[J]. 仪器仪表学报, 2019, 40(8): 158-166.

[6] CHEN P T, SPEYER J L, MAJID W A. Frequency stability analysis of pulsar-aided clocks[J]. Navigation, 2019, 66(3): 1-12.

[7] 赵书红, 董绍武, 白杉杉, 等. 基准频标与守时频标联合的频率驾驭算法研究[J]. 仪器仪表学报, 2020, 41(8): 67-75.

[8] 杨廷高, 高玉平, 童明雷, 等. 综合脉冲星时研究进展[J]. 航空学报, 2023, 44(3): 54-70.

[9] PETIT G, TAVELLA P. Pulsars and time scales[J]. Astronomy & Astrophysics, 1996, 308: 290-298.

[10] MATSAKIS D N, FOSTER R S. Application of millisecond pulsar timing to the long-term stability of clock ensembles[J]. Amazing Light, 1995: 445-462.

[11] MATSAKIS D N, TALOR J H, EUBANKS T M, et al. A statistic for describing pulsar and clock stabilities[J]. Astronomy & Astrophysics, 1997, 326(3): 924-928.

[12] PÍRIZ R, GARBIN E, ROLDAN P, et al. PulChron: a pulsar time scale demonstration for PNT system[C] // Proceedings of the 2019 Precise Time and Time Interval Meeting, ION: Virginia, 2019: 28-31.

[13] EDWARDS R T, HOBBS G B, MANCHESTER R N. Tempo2, a new pulsar timing package-II. The timing model and precision estimates[J]. Monthly Notices of the Royal Astronomical Society, 2006, 372: 1549-1574.

[14] 童明雷, 杨廷高, 赵成仕, 等. 脉冲星计时模型参数的测量精度分析与估计[J]. 中国科学(物理学 力学 天文学), 2017, 47(9): 99-108.

[15] BACKER D C, DEXTER M R, ZEPKA A. A programmable 36 MHz digital filter bank for radio science[J]. Astronomical Society of the Pacific, 1997, 109: 61-68.

[16] PERERA B B P, DECESAR M E, DEMOREST P B, et al. The International Pulsar Timing Array: second data release[J].Monthly Notices of the Royal Astronomical Society, 2019, 490(4): 4666-4687.

Preliminary study on the establishment of composite time scales of pulsar time and atomic time

ZHU Xing-zhi, TONG Ming-lei, ZHAO Cheng-shi

(National Time Service Center, Chinese Academy of Sciences, Xi’an 710600, China)

Atomic time has high short-term stability, and pulsar time based on the rotation of millisecond pulsars has high long-term stability. The integration of the two can construct a time scale that combines both long-term and short-term stability advantages. This article preliminarily constructs a composite time scale (composite timescale, CT) for the combination of pulsars and atomic clocks through the classical weighted average algorithm. Based on the latest atomic time data of TA(NTSC)-TAI published by BIPM, and selecting the four pulsars with the highest timing accuracy published by the International Pulsar Timing Array (IPTA), CT is obtained through a combination of parallel weighting and classification weighting. The results show that the CT’s stability obtained by parallel weighting is significantly improved within 10 years compared with each pulsar, and the stability is close to that of pulsar J0437-4715 with high stability in 4 to 10 years. The stability results of CT weighted by classification and parallel weighting have significant advantages at both ends of the time span, reaching 5.1×10-15in 0.26 years, and 1.0×10-15in 16.8 years, and the stability of CT obtained from 4 stars was significantly improved compared to that by 2 pulsars after 5.2 pulsars.CT obtained by the classification weighting method has a smaller deviation compared to TAI, and the time scale is more stable. In conclusion, the short-term stability of atomic clock group can suppress the short-term noise of pulsar clock group, while pulsar time can improve the long-term stability of comprehensive time scale CT.

time scale; pulsar time; atomic time; frequency stability

朱幸芝，童明雷，赵成仕. 脉冲星时与原子时联合时间尺度建立初步研究[J]. 时间频率学报, 2023, 46(3): 198-205.

10.13875/j.issn.1674-0637.2023-03-0198-08

2023-03-28；

2023-05-26

科技部SKA专项资助项目（2020SKA0120103）；国家自然科学基金资助项目（U1831130、11973046）；中国科学院“西部之光”人才培养计划“西部青年学者”资助项目（XAB2021YN27）