关于脉冲星时定义的初步探讨

何婷，郑勇

关于脉冲星时定义的初步探讨

何婷，郑勇

（中国人民解放军战略支援部队信息工程大学，郑州 450001）

毫秒脉冲星作为新发现的稳定频率源，为新的时间计量标准的产生奠定了物理基础。基于毫秒脉冲星自转周期建立的脉冲星时间计量基准，对人类拓展时间计量及应用的时空维度，提升时间标准精度、安全性等方面具有重要意义。目前学术界对脉冲星时的研究主要集中在如何通过长期的脉冲星计时观测，实现对脉冲星计时模型的持续修正和精化。从严格意义上说，脉冲星时尚未有一个明确、完整的定义。这既不利于对脉冲星时的科学理解和研究，也不利于其时间计量基准的标准化、规范化建立及维持与应用。为此，论文在回顾总结现有时间计量标准定义及其发展的基础上，依据时间计量标准定义的基本惯例，遵循独立性、可测性、稳定性、一致性、可复制性和可用性原则，提出了脉冲星时的初步定义，包括脉冲星时起点、秒长的定义等；探讨了脉冲星钟设计及脉冲星时建立、维持与应用的初步思路。本文内容只是个人观点，希望能为脉冲星时的定义提供参考，为脉冲星钟的研制提供新的角度和思路。

时间计量标准；原子时；脉冲星时；脉冲星时定义

0 引言

时间计量标准的选择和定义，是人类认知时间、应用时间的重要依据。我国西汉古籍《淮南子》中就有：“天设日月，列星辰，调阴阳，张四时”的论述。太阳和月亮的视运动体现为一种恒常的、循环往复的周期现象，古人在对日、月等天象及其运动的长期观察中体悟到了不可见的时间，也由此诞生了最初的计时和纪时行为，包括：公元前2000年古巴比伦的日晷计时、中国的香漏计时，公元前1500年古埃及的水钟计时，公元前700年中国的立表测影，公元900年英国的蜡烛钟计时，15世纪欧洲的沙漏计时等。公元前300年中国制定并颁行了颛顼历，公元前45年古罗马执政官儒略·凯撒施行了儒略历[1]。观象授时标志着古人对时间的认识和实际应用达到一个高峰，同时也是人类进一步探索时间之质和时间之量的发端。以观象授时为起点，人类的计时技术历经了漫长的发展历程，取得了辉煌的成就，从早期的日晷、香漏、水钟（漏刻）、蜡烛钟、沙漏等，到天文钟、机械钟、石英钟、原子钟，再到当前已成为新的发展方向的光钟和脉冲星钟等。计时技术的持续发展，即对于更稳定、更精准的频率标准的持续探索，推动了时间计量标准的产生及变迁。

计时器（钟）由两大核心要素构成：一是频率标准，其产生的周期性物理事件（信号）是构建秒长或其他基本时间尺度的物理基础；二是累加器，它从确定的起点（时刻校准点）开始，对计时器建立的基本时间尺度进行累加，从而确定时刻[2]。计时器的计时精度主要取决于起点的校准偏差，以及基于频率标准构建的基本时间尺度的准确度、稳定度和对于环境扰动（温度变化、磁场变化、干扰及噪声）的敏感程度等。由此，起点和基本时间尺度构建方法的定义就成为时间计量标准定义的核心。

随着科技的飞速发展、生产力的大幅提高、计时技术的日趋成熟，时间计量标准应运而生。在此之前，世界各地普遍采用的是地方时，它由本地天子午圈与太阳所在赤经圈的夹角（时、分、秒表示）确定。任何经度上的微小差异，都会造成地方时的不同，即任何经度不同的地点都有自己的地方时，从而造成了世界范围内时间的混乱。这给世界各国日益频繁的国内和国际交通造成了很大的不便，特别是在铁路交通迅速发展以后，地方时因经度不同而不同的缺点显得更加突出。1878年，加拿大铁路工程师弗莱明提出用分区计时的办法来解决这个问题，统一全世界的时间。1884年在美国华盛顿举行的国际子午线会议采纳了该建议，建立了以格林尼治时间为核心的时间体系，由此诞生了人类历史上第一个全球统一的时间计量标准——世界时。

时间计量标准的定义，需着重考虑依据该标准所建立的时间尺度的准确性、稳定性，所建立的时间计量系统工作的连续性及可复制性，所计量出的时间应满足人类的习惯性等因素。天文学及物理学的发展，计时技术的突破，对精度和稳定性的不懈追求，推动了时间计量标准的持续发展和变迁。继世界时之后，又相继提出了历书时、国际原子时和协调世界时。当前国际上法定的时间计量标准为协调世界时。未来也一定会发展出基于更高性能计时器的新的时间计量标准。

因此，时间计量标准的定义，始终代表着计时技术和频率标准技术发展的最新水平，对人类生产、生活和科学研究等产生基础性的、广泛而深远的影响。

1 现有时间计量标准的定义及发展

秒是计量时间的基本单位，秒长的确定问题是时间计量标准定义的根本问题。确定秒长需要持续、稳定的周期现象作为参照。地球的自转及公转所伴随的昼夜交替、四季轮回的周期现象为人类确定秒长提供了天然的物理参照，这是世界时、历书时定义的基础。第一台实用型铯原子频标研制成功后，人类对于恒常周期物理参照的探索从宏观世界深入到微观世界，原子跃迁所辐射的频率高度准确和稳定的电磁波，成为原子秒及原子时定义的物理基础。

1.1 世界时

1884年美国华盛顿国际子午线会议的决议[3]指出：“会议建议采用世界日（universal day），同时不影响在必要情况下使用地方时。上述世界日为平太阳日，考虑将人类习惯的一日的起始时刻与通过天文观测定义的一日的起始时刻相协调，设计世界日的起始时刻为本初子午线的午夜时刻，并且按照从0至24时的方式计时。”根据上述决议，英国格林尼治天文台观测得到的由平子夜起算的平太阳时称为世界时，记为UT（Universal Time），起点为1858年11月17日零时。1960年以前，世界时是国际上统一采用的时间计量标准。

平太阳时是以平太阳的周日视运动为依据建立的时间系统。它以平太阳在当地连续两次上中天的时间间隔为一个平太阳日，并以平太阳在当地上中天瞬间作为平太阳日开始。由于人们习惯于一天从子夜开始，根据习惯性原则，平太阳时定义改为：平太阳时角+12ʰ。一个平太阳日分为24平太阳时，1平太阳时分为60平太阳分，1平太阳分分为60平太阳秒。

世界时定义后，经历了极移改正和地球自转速率季节性变化改正，分别记为UT1和UT2。即使进行了季节性变化的改正，地球自转速率仍然存在长期变慢的趋势以及不规则的变化。地球自转速率的不均匀性意味着世界时的基本尺度“日”在逐渐变长且存在不规则变化，由此定义的标准秒长，也存在相应的变化。虽然天文学家一直在研究世界时秒长中地球自转不规则变化的修正方法，其均匀性和精度也只能达到10-8量级[4]。尺度的非均匀性使得世界时不再适合作为更高精度时间计量的标准。但是由于人类生活在地球上，其活动与地球自转及太阳周日视运动密不可分，所以世界时仍具有难以替代的作用和地位。目前应用最广泛的世界时是UT1，因为它直接反映了地球表面一点相对于天球参考系的精确角位置，在精密定位与导航、测地等领域具有重要的应用[4]。

1.2 历书时

历书时（Ephemeris Time，ET）是以地球公转运动为依据建立起来的计时系统，起点是世界时1900年1月1日12时，基本时间尺度是一回归年长度。历书时是1960年至1966年国际上采用的，继世界时之后的第二个时间计量标准。

地球的公转速率虽然时快时慢，但公转周期（即一回归年）是非常稳定的。一回归年指地球在公转过程中两次经过轨道上同一点所需要的时间间隔。以历书时1900年1月1日12时起算的回归年长度作为标准，将这一年长度的1/31 556 925.974 7（365.242 2×24×60×60），即这一年的平太阳秒作为1秒的固定长度，称为历书时秒（用于制订天文历书的标准秒）。1960年第十一届国际计量大会[5]决定采纳历书时秒作为秒长的新定义：“秒是1900年1月1日历书时12时起算的回归年的 1/31 556 925.974 7。”

历书时秒在理论上是一种均匀的时间尺度，但实际应用中不太容易得到，且很难保存。由于技术上的原因，一般通过观测月亮来测定历书时。实际测定过程中，月面形状和边缘的不规则性，以及地球—月球潮汐作用引起的月球减速，都会影响测量的准确度，加上天文观测仪器本身的精度所限，综合三年的观测资料得到的历书时秒的精度只能达到10-9量级[1]，仍然满足不了现代科学技术发展的需求。尽管如此，历书时秒仍作为一个天文常数保存下来，在大地测量和天文学的研究上有重要的参考价值。

1.3 原子时

原子时的提出与实用型原子钟的研制及发展密不可分。原子钟的构想是由诺贝尔奖得主拉比（I. I. Rabi）在20世纪40年代早期提出的。1949年，美国国家标准局的哈罗德·莱昂斯（H. Lyons）向世界推出了第一台原子钟，该原子钟基于氨分子的谐波共振，应用了微波光子吸收原理，其稳定度与地球自转速率相当，但不能够像一台实用的工作时钟那样持续运转。尽管如此，氨分子钟的成功研制，使时间计量标准的定义在哲学及科学意义上均迈出了重要的一步。20世纪50年代早期，莱昂斯的团队研究了使用铯束作为原子频率标准的可能性，这项开创性的工作展示了高精度原子频率标准的潜力。1955年6月，英国皇家物理实验室的艾森（L. Essen）和帕里（J. V. L. Parry）研制推出了世界上第一台实用型铯原子钟[2]。

20世纪50年代实用型铯原子钟的成功研制为秒长的重新定义提供了新的方向、思路以及现实可能。1967年第十三届国际计量大会定义了原子时秒长：“秒是铯133原子基态的两个超精细能级之间跃迁所对应的辐射的9 192 631 770个周期的持续时间[6]。”该秒长定义被国际单位制（International System of Units，SI）采纳并沿用至今。同时，大会决定采用新的时间计量标准——原子时（Atomic Time，AT），这是人类历史上定义的第3个时间计量标准。原子时的秒、分、时、日、月、年的换算关系仍与世界时相同，起点是世界时1958年1月1日零时，这一瞬间要求原子时与世界时完全重合，但由于技术上的原因，存在0.003 9 s的差值，该值作为一个历史事实被永久保存下来。

与世界时和历书时不同，原子时的建立不再基于天文观测，而是基于原子钟。将某台原子钟的起点校准后，从该起点开始，对该原子钟复现的秒长进行累加，就得到了原子时。但原子钟作为仪器设备，有自身的寿命，存在发生故障的风险，且受环境因素及自身技术指标影响，输出频率存在偏移、漂移和随机抖动。上述因素使得基于单台原子钟建立的原子时在准确性、稳定性及工作的连续性上均得不到保证，因此，原子时的构建需基于原子钟组。

根据构成钟组的原子钟的来源，可将原子时划分为地方原子时和国际原子时。由一个时间实验室若干台原子钟或一个地区若干时间实验室的原子钟组成的钟组导出的原子时，称为地方原子时，记为TA()。其中表示建立地方原子时的时间实验室的简称。分布在世界范围内的各时间实验室共同协作可显著提高原子时的稳定性。1971年，第十四届国际计量大会指定由国际计量局（International Bureau of Weights and Measure，BIPM）根据SI时间单位秒的定义，以世界各地时间实验室运转的原子钟读数为依据，经相对论修正并归算到平均海平面上所建立的原子时间系统称为国际原子时，命名为TAI（Temps Atomique International or International Atomic Time）：“国际原子时是国际时间局根据国际单位制中时间单位秒的定义，依据世界范围内各守时实验室运行的原子钟的读数而确定的时标[7]。”当前，TAI由参与国际协作的八十多家时间实验室的五百多台自由运行的原子钟经加权平均（优化其时间尺度的长期频率稳定度）和频率驾驭（使其时间尺度符合SI秒长定义）产生，准确度及稳定度均达到10-15～10-16量级，是实际应用中具有权威性、代表性的高性能时间计量系统。TAI是纸面时间，需事后数据处理，滞后一个月以时间公报的形式由BIPM发布，告知相关时间实验室其上个月以5 d为间隔的TA()相对于TAI的差值，相关时间实验室利用该差值得到TAI。

随着原子钟技术、高精度时频传递技术的持续发展以及数据处理算法的优化，目前基于铯喷泉钟和光钟实现的SI秒长的实际复现精度可达10-16～10-18量级，成为国际单位制七个基本单位中，计量精度最高的物理量，并且相对于世界时和历书时的秒长，它更容易测定和应用，不需要进行长时间的天文观测。高度准确、稳定、且应用方便的原子时更符合科学研究和工程应用的需求，而人类活动更习惯于世界时。原子时秒长与世界时秒长存在差异，且由于地球自转速率存在的不规则变化和长期变慢趋势，随着时间的增长，两者秒长差异日益增大，原子时将逐步偏离世界时，从而导致原子时时间尺度（秒长）的精确性与世界时时刻的不均匀性之间的矛盾。

1.4 协调世界时

协调世界时（Coordinated Universal Time，UTC）不是一种独立的时间计量标准，而是由国际原子时（TAI）与世界时（UT1）协调后产生的，起点是世界时1960年1月1日零时。UTC自1972年1月1日起在全世界实施，并正式被确立为国际标准时间，成为世界各国的官方时间。

由于采用了相同的时间尺度（秒长），UTC和TAI的尺度建立方式相同，UTC本质上仍是原子时。在时刻上，两者相差整秒，即从TAI中减去正确的闰秒数就是UTC。

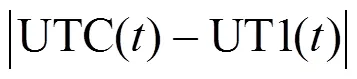
2 建立脉冲星时间基准的意义

2.1 毫秒脉冲星及其基本物理特性

脉冲星诞生于超新星爆发过程中大质量恒星内核的塌缩，是高速旋转的磁化中子星。中子星在旋转过程中会产生极高的能量，这些能量会以高强度的电磁辐射形式（脉冲星辐射跨整个电磁频谱，从无线电波、可见光，到X射线、伽马射线），散射到宇宙空间中[9]。中子星具有非常强的磁场，在磁极冠的开放磁力线区域中，带电粒子在磁场中运动发出曲率辐射，形成以磁轴为中心的方向性很强的束状电磁波束[10]。由于磁轴与自转轴不重合，在中子星自转的同时，其辐射的电磁波束就像灯塔一样扫过不同的方向。部分中子星每自转一周，它的电磁波束就会扫过地球一次或两次，地球上的观测者借助射电望远镜可观测到有规律的电磁脉冲。这些中子星独有的电磁脉冲令它们得名“脉冲星”。从1967年发现射电脉冲星到1974年发现射电脉冲双星，形成了脉冲星研究的一次高潮[10]。1982年毫秒脉冲星PSR B1937+21的发现，引起学术界的高度关注，再次形成脉冲星观测研究的高潮[10]。毫秒脉冲星与之前发现的脉冲星的特性迥然不同，是一种新类型的脉冲星，具有自转周期短（毫秒量级）、年龄老（约1010年）、表面磁场弱（108～1010Gauss量级）等特性[9]。毫秒脉冲星被认为是从X射线双星演化而来的[10]。在X射线双星阶段，中子星接受来自伴星的物质，不仅辐射X射线，而且吸积物质带来的角动量使中子星的自转不断加快，其自转周期可低至毫秒量级[10]。目前，发现的脉冲星数目已接近3 000颗，其中毫秒脉冲星约200颗。发现的毫秒脉冲星中，约80%为双星系统，另外20%为孤立毫秒脉冲星[10]。

脉冲星具有非常稳定的自转周期，在宇宙天体中是绝无仅有的[10]，其自转周期表达式如式（1）所示[11]：

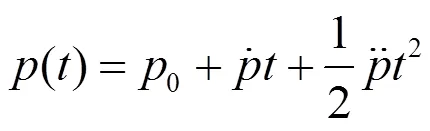
毫秒脉冲星的自转周期稳定性要远高于普通脉冲星。目前周期测量最准确的脉冲星是PSR J0437-4715，其在约化儒略日MJD（51 194）的自转周期为（5.757 451 831 072 007±8×10-15）ms，已精确到10-15ms[10]。毫秒脉冲星也存在自转减速，周期随时间十分缓慢的增加，但比普通脉冲星约低5个数量级，周期变化率在10-19～10-21之间。周期变化最慢的脉冲星是PSR J2322+2057，每秒变长7.1×10-21s[10]。

脉冲星自转周期除了有规律的减速，还存在随机变化，称之为计时噪声。年轻脉冲星的计时噪声比较大，毫秒脉冲星年龄老，计时噪声相比普通脉冲星要小的多。产生计时噪声的物理机制并不十分清楚，很可能与中子星内部的超流及温度变化有关，也可能与发生在磁层中的某些过程有关。老年脉冲星的计时噪声比较小是非常重要的发现，这意味着老年脉冲星的时间测量精度可以很高。毫秒脉冲星的计时噪声普遍很小，周期的长期稳定性非常高。一年以上的观测表明，毫秒脉冲星的周期稳定度普遍优于10-12，有近20颗毫秒脉冲星的周期稳定度约为10-14，有6颗优于10-14 [10]。

2.2 建立脉冲星时的意义

毫秒脉冲星独特的物理特性，即自转周期的精确可测性和高度稳定性，使其具备作为一类独立的、天然的频率标准的条件和优势；基于毫秒脉冲星的自转周期定义脉冲星时，具备理论上、物理上的合理性。虽然当前原子时的应用已经相当的普遍和广泛，但脉冲星时的建立亦具有以下3方面重要的价值和意义：

① 从空间维度来看，人类活动已经拓展至深空。深空探测、深空导航等应用对时间精度的要求很高，而如何在深空获取和维持精密的时间标准，是一个至今仍未解决的难题。在地面上，我们有高性能的原子钟，但受准确度、稳定度、复杂度、体积、重量、寿命、宇宙极端环境（相对论效应、辐射、温度、磁场）等因素限制，深空原子钟的研制异常困难。直至2019年，美国国家航空航天局（National Aeronautics and Space Administration，NASA）发射了一台深空原子钟到近地轨道进行测试。该钟为离子阱频标，由NASA喷气推进实验室开发[12]。NASA希望深空原子钟能在21世纪30年代早期应用于引导宇宙飞船。相比尚处于起步阶段的深空原子钟，利用毫秒脉冲星进行定时和自主导航在技术上更为成熟，并且引力势环境简单，可同时获得精确的时间信号和空间位置坐标，在应用上更加实际，可以认为脉冲星时在深空应用中具有显著的优越性。

② 从时间维度来看，人类需要建立在数百年时间跨度下维持高稳定度的时间基准。深空航天器飞出太阳系、飞出银河系，需要数百年的时间，上述超长稳时间基准必将成为重要支撑。原子时的稳定度是通过参与国际原子时合作的、分布于全球的、大量独立运行的原子钟的钟面时依据综合原子时算法加权平均保证的，准确度是通过基准原子频标及二级原子频标的频率驾驭保证的。然而，当将时间跨度扩展至数十年、数百年，甚至更长久时，即使发展了性能更优良的原子钟以及更优化的算法，原子时的稳定度也很难测量和维持。而基于毫秒脉冲星自转运动构建的脉冲星时在长期稳定性方面具有明显的优势。观测研究表明，一些毫秒脉冲星长期的时间稳定度优于原子钟，如PSR J0437-4715、PSR B1855+09，观测时间越长，周期稳定度越高[10]。作为独立于地球的、完全不同于原子时的、能够在相当长的时间尺度范围内有效运转并保持高稳定性的时间源，脉冲星时具有成为时间计量标准的价值和潜力，可同原子时相互取长补短、互为补充，如利用脉冲星时补偿原子时在长期稳定度方面的缺陷，校正、改进原子时的长期稳定度。

③ 从安全性考虑，时间计量标准的应用依赖于精密、安全、可靠的授时手段。目前，原子时的发播有GNSS卫星授时、长波授时、短波授时、低频时码授时、网络授时、光纤时频传递等多种手段，其中GNSS卫星授时以其覆盖范围大、精度高的优势成为最主流的在各领域应用最广泛的授时方式。但GNSS卫星授时所固有的脆弱性，即易受干扰和欺骗的影响，使其在应用过程中存在较大的安全隐患。当前解决该问题的主要途径是采用多手段冗余授时，但因各授时手段在同步精度、覆盖范围、部署便利性及灵活性等方面存在差异，该途径并不能够真正解决原子时的有效传递问题。而脉冲星时为上述问题的解决提供了新的思路。作为完全独立于原子时的时间系统，脉冲星时具有特有的尺度建立方式及时间传递方式，其在抗打击（脉冲星处于深空）、抗干扰（射电望远镜视野开阔、工作频率宽、灵敏度高、环境适应性好）、抗欺骗（射电望远镜可同时接收、处理多颗脉冲星信号）方面具有显著优势，可为终端侧的授时安全检测提供可信的冗余时间计量标准参照。

以上分析表明，脉冲星时能够极大的拓展原子时间系统及其应用的空间、时间及领域范围，完全有其存在的必要性和合理性。以发展的眼光来看，脉冲星时并不一定要替代原子时，同样原子时也无法替代脉冲星时，考虑到未来时间频率应用的广度、深度和复杂性，多元化的、优势互补的时间计量基准将成为一种必然趋势。

3 定义脉冲星时的初步研究

3.1 研究脉冲星时定义的意义

当前，学术界对于脉冲星时的研究主要集中在通过长期的脉冲星计时观测对脉冲星计时模型进行持续的修正和精化，脉冲星时由脉冲星计时模型表达，借助脉冲星计时观测建立。根据各噪声源特点，对多颗脉冲星定义的脉冲星时进行加权平均，可建立具有更高长期稳定度的综合脉冲星时[13-25]。但是严格意义上来说，脉冲星时尚未有一个明确的、完整的定义，体现为脉冲星时的起点未定义、基本时间尺度的建立方法未定义、脉冲星时秒长未定义等。上述定义的缺失不利于脉冲星时的科学理解及其标准化、规范化应用。

脉冲星时的定义是推动其成为一种独立的时间计量标准的基础和前提。回顾时间计量标准的发展史，每一种标准都有科学、明确的定义，以及起点、基本尺度、秒长等完整的要素。同世界时、历书时及原子时一样，脉冲星时也应拥有自己的频率标准（毫秒脉冲星自转频率）和累加器（到达脉冲计数）等，这是作为一种独立时间标准所应具备的必要条件。目前对脉冲星时概念的描述，基本上都落脚到脉冲星计时模型上，这一方面不够直接，缺少必要的要素定义，与其他时间计量标准的定义非同一语系；另一方面，脉冲星计时模型的建立（观测及数据处理）及表达，均以原子时为参考，而依赖原子时，必受其影响和制约，在原子时基础上定义脉冲星时，从计量标准的角度考虑是矛盾不合理的。因此，要推动脉冲星时成为一种新的、独立的时间计量标准，就必然要从时间计量标准定义的逻辑和原则出发去定义脉冲星时。

研究确定科学、严密、完整的脉冲星时定义，是统一认知、实现其标准化应用的必然要求。当前，无论是基于单颗毫秒脉冲星计时观测建立的单脉冲星时，还是基于脉冲星计时阵观测建立的综合脉冲星时，在实际应用中，都无法对这些脉冲星时系统实现真正意义的统一。根本原因在于脉冲星时间计量标准未定义，脉冲星时相互之间的比对和尺度校准缺失了参考基准，即便是综合脉冲星时，也是建立在原子时参考基准上的综合。从而造成了脉冲星时从属于、服务于原子时的应用现状，限制了脉冲星时精度的进一步提升以及脉冲星时应用的广度和深度的进一步拓展。从统一认知、促进脉冲星时标准化应用及长远发展的角度考虑，有必要进一步完善当前脉冲星时的概念，站在更宏观的层次上研究如何科学的定义脉冲星时。

3.2 定义脉冲星时的原则

脉冲星时的定义，需以现有的脉冲星计时观测资料及计时研究成果为基础，同时遵循以下原则：

① 独立性原则。以毫秒脉冲星自转这一恒常周期现象为参考，定义脉冲星时秒长，使脉冲星时成为独立运行的时间计量系统。

② 可测性原则。突破当前的脉冲星计时观测模式，定义不依赖于原子时的脉冲星时间尺度建立方法，确保脉冲星时建立与维持具备实际可行性。

③ 稳定性原则。脉冲星时的定义需保证其基本时间尺度在长期稳定度方面的显著优势，同时尽可能提高短期稳定度。

④ 一致性原则。借助脉冲星时秒长的定义，统一各脉冲星计时系统（及脉冲星计时阵）的时间，即保证脉冲星时秒长的唯一性，维持各系统实际建立秒长与脉冲星时秒长的一致性。

⑤ 可复制性原则。脉冲星时间尺度建立方法的定义，需保证实际建立的脉冲星计时系统在全球范围内可复制，必要时可拓展至深空，并保证一定的计时精度。

⑥ 可用性原则。脉冲星时的定义需考虑实际建立的脉冲星时的实时性、连续性、安全性以及可传递、可驾驭等应用需求，保证脉冲星时在尽可能广的领域具备可用性。

3.3 脉冲星时的初步定义

根据独立性、可测性和一致性原则，本文建议基于一颗优选的毫秒脉冲星的自转周期定义脉冲星时秒，定义该毫秒脉冲星源为基准毫秒脉冲星。根据稳定性原则，基准毫秒脉冲星的选择可从如下几个方面综合考虑：参数测量精度高；自转周期稳定，计时噪声小；脉冲轮廓窄、无明显轮廓模式变化；接收信号具有较高的信噪比；观测数据时间跨度长；计时残差均方根值低。

基于以上原则，本文建议以PSR J0437-4715作为基准毫秒脉冲星。PSR J0437-4715是一颗距离地球较近的X射线毫秒脉冲星，属于双星系统的一颗，是澳大利亚Parkes天文台的64 m射电望远镜于1992年7月11日在430 MHz的“南天毫秒脉冲星巡天”观测中发现的，其主要参数和特性如下：

① PSR J0437-4715的历表参数在已发现的同类脉冲星中，目前的测量精度是最高的。其自转参数测量精度为：频率误差约6×10-15Hz，频率一阶导数误差约7×10-23s-2；天体测量参数测量精度为：赤经误差约15μas，赤纬误差约100 μas，赤经自行误差约0.5 μas·yr-1，赤纬自行误差约0.5 μas·yr-1，视差误差约30 μas[20]。

② PSR J0437-4715为当前发现的最稳定的毫秒脉冲星。5年观测获得的周期稳定度达到10-15 [10]，计时噪声小。建立的单脉冲星时间稳定度达到3.3×10-14/yr，1.23×10-15/10 yr[26]。

③ PSR J0437-4715辐射的射电脉冲宽度窄，且轮廓形状稳定[27]。

④ PSR J0437-4715是拥有强射电辐射的毫秒脉冲星之一，信噪比高，例如其在1.4 GHz的统计平均流量为150 mJy[28]。

⑤ PSR J0437-4715是澳大利亚PPTA（Parkes Pulsar Timing Array）常规监测的20颗毫秒脉冲星之一，每两到三周进行一次计时观测，每次持续观测1 h，观测数据时间跨度达二十多年。

⑥ PSR J0437-4715是目前计时精度最高的源，计时残差均方根达到108 ns[16]。历史计时观测结果：2008年，J. P. W. Verbiest学者对J0437-4715的10年观测数据进行了处理，得到计时残差为200 ns，预期精度可达100 ns。2009年，G. Hobbs研究员[29]处理J0437-4715的1年3 GHz频段的数据，计时残差结果为60 ns，单次观测计时残差精度最高达30 ns。

⑦ PSR J0437-4715在MJD（51 194）的自转周期为（5.757 451 831 072 007±8×10-15）ms，自转频率为（0.173 687 948 999 098 3±3×10-16）kHz。

基于上述自转参数，本文建议的脉冲星时秒长定义为：毫秒脉冲星J0437-4715在其固有参考架下，连续自转173 687 949周所持续时间的1/1 000 000。

根据PSR J0437-4715自转周期，可计算出上述定义的脉冲星时秒长的理论值为（1.000 000 000 005 191±1.389 503 592×10-15）s，其精度为5.2×10-12量级。

本文建议脉冲星时的起点定义为：某确定台站（可由国际计量大会推选）在某确定时间段内观测PSR J0437-4715，所测站心TOA数据中最接近UTC整秒的时刻点。

3.4 脉冲星钟的初步设计思路

根据可复制性和可用性原则，本文建议上述定义的脉冲星时的建立与维持以脉冲星钟为基础。同时建议脉冲星钟的初步设计思路如下：以观测台站的射电望远镜接收的PSR J0437-4715毫秒脉冲星周期性射电脉冲信号为参考，以原子频标为实用频标，将实用频标输出的1 PPS信号与射电脉冲信号进行连续比对，比对周期为1 000 000脉冲星时秒（即每1 000 000脉冲星时秒进行1次比对），周期的起始时刻及终止时刻由射电脉冲参考点标识。射电脉冲参考点定义为经台站信号处理之后的射电脉冲峰值点。在初始时刻（第1个比对周期的起始时刻），通过技术手段实现实用频标输出的1PPS与射电脉冲参考点之间的严格同步，之后每1 000 000脉冲星时秒所对应时刻点进行一次射电脉冲参考点与实用频标1 PPS之间的比对，记录钟差数据。累积一定数量的钟差数据，建立脉冲星钟钟差模型。依据钟差模型，对实用频标进行开环驾驭，实现脉冲星钟。对脉冲星钟进行校准，从校准时刻开始对产生的1 PPS进行计数，即可实现计时。基于不同的射电望远镜，不同的原子频标，可构建不同的脉冲星钟。脉冲星钟作为实体设备，其输出信号及数据接口建议为标准接口，以便于采用现有技术、设备及系统实现脉冲星钟输出时间频率信号的传递、测量与比对。

脉冲星时的建立与维持可基于UTC系统，即在有射电脉冲接收条件的各时间实验室的主钟基础上建立脉冲星钟，从而建立与维持地方脉冲星时，本文记为PT()。由国际计量局基于各时间实验室的PT()及统一的综合脉冲星时算法，建立国际脉冲星时。基于国际脉冲星时对各时间实验室的脉冲星钟进行二次驾驭，保证PT()与国际脉冲星时的差在规定范围内。上述脉冲星时的建立思路可充分利用当前的UTC系统资源，同时也利于实现UTC与国际脉冲星时两套时间计量基准的长期共存。

在地面及近地空间，用时系统可根据实际需求，选择以UTC为参考，或者以国际脉冲星时为参考。考虑到脉冲星时的秒长精度以及短期稳定度不如原子时，其优势主要在于长期稳定度，本文建议超长期（10年及以上）的时间应用以国际脉冲星时为参考，其他应用以UTC为参考。例如以国际脉冲星时为参考，对时间实验室地方原子时TA()进行精度维持与性能监测。原子时的基本特点是具有良好的短期稳定度，但受频率漂移的影响，其长期稳定度不如脉冲星时。当前，各时间实验室主要依靠铯/氢原子钟进行守时，其频率精度在10-12～10-13Hz量级，据此可推导出，一台铯钟或一台氢钟守时一年，由频率漂移引入的时间不确定度约在几十微秒量级[30]。考虑到脉冲星时的长期自主维持精度优于地方原子时TA()，因此可基于脉冲星时实现TA()的自主精度维持，而无需与TAI或地球时TT（Terrestrial Time）进行比对。将TA()的1PPS信号与经过二次驾驭的PT()（国际脉冲星时的本地实现）的1PPS信号按照预设测量周期进行连续钟差测量，依据实测的钟差数据对TA()实施定期校准。脉冲星时服务建议采用申请、授权模式，各地方脉冲星时的建立与维持单位可通过TWSTFT（two-way satellite time and frequency transfer）、卫星共视、光纤等方式向授权用户定点传递PT()。

在深空应用中，可基于本文建议的脉冲星钟设计思路在航天器上构建脉冲星钟，作为航天器时间基准。航天器载脉冲星钟的校准，可在航天器尚处于近地空间时，通过航天测控系统，将地面时统系统建立与维持的脉冲星时的时标信号传递至航天器。校准后，航天器载脉冲星钟自主独立运行，无需地面测控。以连续接收的PSR J0437-4715射电脉冲信号为参考，通过频率、相位的准实时调整（开环驾驭），维持频率精度及计时精度，实现自主守时。如航天器载脉冲星钟内部的实用频标（原子频标）在深空中的短期稳定度无法满足实际需求，建议采用接收X射线脉冲星信号，借助锁相环路，锁定实用频标的频率和相位的方法[19-31]，实时修正实用频标的偏移和漂移，提升开环驾驭间隔内实用频标的性能。

4 结语

严谨、完整的脉冲星时定义是推动其技术发展，促进其广泛应用的基础和前提。本文系统梳理了时间计量标准定义的历史沿革及发展，进而延伸探讨了脉冲星时的意义，分析了定义脉冲星时的意义及准则，提出了脉冲星时的初步定义。在本文的脉冲星时初步定义中，建议了脉冲星时的起点、秒长、脉冲星钟的初步设计思路以及脉冲星时建立、维持及应用的初步思路，可为未来脉冲星时的定义提供参考。在本文研究的基础上，后续需进一步论证PSR J0437-4715作为基准毫秒脉冲星的合理性，脉冲星时起点、秒长定义的合理性，地面、深空脉冲星钟研制的实际可行性等基本问题，同时需开展脉冲星钟驾驭算法、综合脉冲星时算法、脉冲星时国际合作等相关机制及关键算法研究。

[1] 王月霞. 时间知识篇(上)、(下)[M]. 呼和浩特: 远方出版社, 2006.

[2] ALLAN D W, ASHBY N, HODGE C C. The science of timekeeping[R]. Hewlett-Packard: Application Note No.1289. Allan’s Time Interval Metrology Enterprise: Fountain Green, 1997.

[3] US Government. International Conference Held at Washington for the Purpose of Fixing a Prime Meridian and a Universal Day[R]. Washington D.C: [s.n.], 1884.

[4] 童宝润. 时间统一系统[M]. 北京: 国防工业出版社, 2003.

[5] COMPTES RENDUS DES SÉANCES. ONZIÈME CONFÉRENCE GÉNÉRALE DES POIDS ET MESURES[R]//Paris: [s.n.], 1960.

[6] COMPTES RENDUS DES SÉANCES. TREIZIÈME CONFÉRENCE GÉNÉRALE DES POIDS ET MESURES[R] //Paris: [s.n.], 1968.

[7] COMPTES RENDUS DES SÉANCES. QUATORZIÈME CONFÉRENCE GÉNÉRALE DES POIDS ET MESURES[R] //Paris: [s.n.], 1971.

[8] 蔡娟, 于连超, 史玉成. 第二十七届国际计量大会通过七项重要决议,为计量科学发展指出新战略方向[EB/OL] (2022-11-23) [2023-02-22]. http://www.ce.cn/cysc/zljd/gd/202211/23/t20221123_38246862.shtml.

[9] BECKER W, KRAMER M, SESANA A. Pulsar timing and its application for navigation and gravitational wave detection[J]. Space Science Reviews, 2018(214): 30.

[10] 吴鑫基, 乔国俊, 徐仁新. 脉冲星物理[M]. 北京: 北京大学出版社, 2018.

[11] AVRAMENKO A. The relativistic inertial coordinate reference frames, synchronized the observed radio emission of pulsar[C]//Physical Interpretations of Relativity Theory, 2017.

[12] BURT E, PRESTAGE J, TJOELKER R L, et al. Demonstration of a trapped-ion atomic clock in space[J]. Nature, 2021, 595(7865): 43-47.

[13] LYNE A G. Pulsars as clocks[C] // European Frequency Time Forum, IEEE Xplore, 1996.

[14] BECKER W, KRAMER M, SESANA A. Pulsar timing and its application for navigation and gravitational wave detection[J]. Space Science Review, 2018(214): 30.

[15] JOSEPH H, TAYLOR J R. Millisecond pulsars: Nature’s most stable clocks[J]. Proceedings of the IEEE, 1991, 79(1): 1054-1062.

[16] 朱幸芝. 毫秒脉冲星时间尺度及钟模型的研究[D]. 西安: 中国科学院国家授时中心, 2011.

[17] 金文敬.脉冲星计时技术及其应用[J]. 天文学进展, 2016, 34(2): 196-211.

[18] 尹东山. 脉冲星计时数据处理与应用研究[D]. 西安: 中国科学院国家授时中心, 2016.

[19] 仲崇霞. 综合脉冲星时算法及脉冲星时应用[D]. 西安: 中国科学院国家授时中心, 2007.

[20] 赵成仕, 童明雷, 高玉平, 等.脉冲星钟模型精度分析[J]. 天文学报, 2017, 58(3): 59-67.

[21] HOBBS G, GUO L, CABALLERO R N, et al. A pulsar-based time-scale from the International Pulsar Timing Array[J]. Monthly Notices of the Royal Astronomical Society, 2020, 491(4): 5951-5965.

[22] GONCHAROV B, BORIS G, REARDON D J, et al. Identifying and mitigating noise sources in precision pulsar timing data sets[J]. Monthly Notices of the ROYAL Astronomical Society, 2021, 502(1): 478-493.

[23] LIU X J, KEITH M J, BASSA C G, et al. Correlated timing noise and high-precision pulsar timing: measuring frequency second derivatives as an example[J]. Monthly Notices of the Royal Astronomical Society, 2019, 488(2): 2190-2201.

[24] HOBBS G, DAI S, MANCHESTER R N, et al. The role of FAST in pulsar timing arrays[J]. Research in Astronomy and Astrophysics, 2019, 19(2): 31-54.

[25] 孙鹏飞. 毫秒脉冲星计时分析及时间尺度研究[D]. 西安: 长安大学, 2020.

[26] 周庆勇, 魏子卿, 张华, 等. 基于双谱滤波的综合脉冲星时算法研究[J]. 天文学报, 2021, 62(2): 86-95.

[27] BRITTON M C, STRATEN W V, BAILES M, et al. High precision timing of PSR J0437-4715[DB/OL]. (2022-12-30) [2023-02-23]. https://articles.adsabs.harvard.edu/pdf/2000ASPC..202...73B.

[28] 李志玄. 利用PSR J0437-4715研究引力常数变化率和台站时钟跳变[D]. 昆明: 中国科学院云南天文台, 2019.

[29] 孙鹏飞, 周庆勇, 焦文海, 等. 脉冲星J0437-4715多终端13年射电数据融合处理分析[C]//中国卫星导航与位置服务第八届年会暨中国北斗应用大会, 郑州: 第八届中国北斗应用大会会务组, 2019.

[30] ZHAO C S, TONG M L, GAO Y P, et al. Analysis of the precision of pulsar time clock model[J]. Chinese Astronomy and Astrophysics, 2018, 42(2): 291-302.

[31] HANSON J E. Principles of X ray navigation[D]. Stanford：Stanford University, 1996.

Preliminary study on the definition of pulsar time

HE Ting, ZHENG Yong

(PLA Strategic Support Force Information Engineering University, Zhengzhou 450001, China)

As a newly discovered stable frequency source, millisecond pulsar may become a physical foundation for the definition of new time measurement standard. Pulsar time defined based on the rotation period of the millisecond pulsar is of great significance in expanding the spatial and temporal dimension of time measurement and improving the accuracy of time standard and the security of timing applications. However, current studies on the definition of pulsar time mainly focus on continuous corrections and refinements of pulsar timing models through long-term pulsar timing observations. Strictly speaking, the definition of pulsar time has not yet been clear and complete, which is not conducive to the scientific understanding and research of pulsar time, nor is it conducive to the standardized establishment, maintenance and application of its time measurement standard. Therefore, on the basis of summarizing the definition of the existing time measurement standards and their development, according to the basic convention of the definition of time measurement standard, and following the principles of independence, measurability, stability, consistency, replicability and usability, the preliminary definition of pulsar time is proposed by this paper, including the definition of starting point and second length of pulsar time and so on; The basic ideas of the design of pulsar clock and the establishment, maintenance and application of pulsar time are discussed. The content of this paper is just a personal opinion, hopefully it can provide a reference for the formal definition of pulsar time, and provide new perspectives for the development of pulsar clocks.

time measurement standard; atomic time; pulsar time; definition of pulsar time

何婷，郑勇. 关于脉冲星时定义的初步探讨[J]. 时间频率学报, 2023, 46(3): 249-259.

10.13875/j.issn.1674-0637.2023-03-0249-11

2023-02-25；

2023-05-23

南京大学“银发双创”资助项目（YFSC202003）