多成分脉冲轮廓模版及其在脉冲星测时中的应用
卢吉光,刘雨兰,姜鹏
多成分脉冲轮廓模版及其在脉冲星测时中的应用
卢吉光1,2,刘雨兰1,2,姜鹏1,2
(1. 中国科学院 国家天文台,北京 100101;2. 贵州射电天文台,贵阳 550000)
部分射电脉冲星存在模式变换现象,射电脉冲轮廓的变化给脉冲星测时工作带来了一定的困难。本文介绍了对存在多种稳定成分的脉冲轮廓进行成分分离的方案,并通过模拟数据实验说明了利用多成分脉冲标准轮廓进行测时优于使用单成分标准轮廓进行测时。
脉冲星;脉冲星测时;模式变换;脉冲轮廓模版;主成分分析
0 引言
射电脉冲星的平均脉冲轮廓通常是稳定的[1],因此可以使用多次观测获得的脉冲轮廓进行叠加获得最终收敛的稳定结果。利用获得的稳定结果或提取其形状特征信息作为标准脉冲轮廓模版,可与单次观测的平均脉冲轮廓进行比对来获取脉冲辐射到达观测站的时间,从而进行脉冲星测时。
然而某些脉冲星的射电脉冲轮廓是不稳定的,会在多种模式中切换[2-6]。如果不同模式之间的特征差别较大,且可以根据单脉冲形状划分到不同的模式中,则不同模式的脉冲轮廓可以对不同模式下的单脉冲进行分别平均计算获得,同时也可以按照不同模式下的脉冲星轮廓分别进行测时以获得好的测时结果。但对于绝大部分发生模式变换的脉冲星,要么辐射强度不足以分辨单脉冲形状,要么单脉冲本身变化较大难以区分其属于哪种辐射模式。因此对于存在模式变换的脉冲星,特定模式下的高精度的标准脉冲轮廓与观测脉冲轮廓难以获得,而对于单个模式持续时间较短的脉冲星这一问题尤其明显。这为高精度脉冲星测时工作带来了极大挑战。
本文将介绍一种通过数学方法获得含有多种成分的脉冲轮廓模版,并使用多成分轮廓模版对脉冲星进行测时的手段,从而有望提高具有多种稳定轮廓成分的脉冲星的测时结果的精度。
1 脉冲轮廓成分分离
本节将介绍对含有多种辐射模式的脉冲星观测轮廓进行成分分离的相关方案。
1.1 脉冲轮廓成分介绍



1.2 经典主成分分析方法
经典主成分分析方法[7]常被用在天文数据分析中,比如斯隆望远镜数字巡天项目(Sloan Digital Sky Survey,SDSS)中的类星体光谱分类[8]和弱引力透镜现象中的点扩散函数变化分析[9]等都使用了经典主成分分析方法。
如果单次脉冲星观测中包含了多种辐射模式,且无法将多种辐射模式精确分离,则可用自助抽样法(bootstrap方法)从观测数据中抽选指定数目的单脉冲叠加形成多个脉冲平均轮廓,而每个平均轮廓都可以视为不同模式的轮廓成分的线性组合。一般情况下,利用长期测时获得的脉冲星星历,在用于对单次脉冲星观测数据进行折叠时,不会在不同周期中导致大的相位偏差,因此可以将此时获得的不同脉冲轮廓的脉冲相位视为已对齐的。即公式(1)可简化为

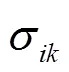
。(5)

1.3 一般情况
经典主成分分析方法对应的求解方式简洁明了,但在很多情况下的数据并不满足其适用条件。比如盖亚探测器(Gaia)的光谱数据中,不同数据的误差不同,因此在进行成分分析时需要考虑不同数据有着不同的权重,即带权重的主成分分析(weighted PCA)[10];在声学领域,很多情况下需要分析的信号不存在确定的起始时间,因此需要采用时移性主成分分析(time-shifted PCA)[11-12]。在实际的成分分析过程中,需要根据实际情况来选取成分分析方法。
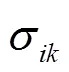
2 数据模拟多成分脉冲轮廓模版在脉冲星测时中的应用
本节将使用数值模拟的方式展示如何在具有模式变换现象的脉冲星数据中提取多成分脉冲轮廓模版,并将它们应用在脉冲星测时中。
本文中所进行的各种数据模拟以及脉冲星测时等操作均为使用python3编程进行,其中绘图部分采用matplotlib模块中的相关函数完成,涉及到函数拟合的部分采用的是scipy.optimize模块中的leastsq函数,以Levenberg-Marquardt算法完成。详细的数据模拟过程如下。
首先,需要模拟存在多种辐射模式的脉冲轮廓。在本文的模拟中,假定脉冲星存在3种不同的辐射模式,生成模拟脉冲轮廓数据的方式如下:① 假定数据中的脉冲星存在3种辐射模式,不同模式下的脉冲轮廓如图1所示;② 考虑不同观测数据中3种辐射的强度在0~1中均匀随机分布,即每次模拟观测数据中的脉冲轮廓为3种模式下脉冲轮廓乘以0~1之间的均匀分布随机浮点数再相加;③ 设定不同位置处的系统噪声强度为0.015,由脉冲星辐射造成的流量起伏为3种辐射模式脉冲轮廓强度之和的0.02倍,利用高斯分布的随机浮点数生成器生成不同相位处的系统噪声与流量起伏;④ 设定不同观测中的相位移动为0~1之间的均匀分布随机浮点数,将模拟数据与系统噪声和流量起伏相加,然后将相位按设定值进行平移,获得模拟脉冲轮廓数据。图2中展示的是模拟数据中的16个脉冲轮廓。可以看到,不同观测中的脉冲轮廓具有不同的形状与脉冲相位。

图1 模拟数据中3种辐射模式下的平均脉冲轮廓

图2 模拟数据中的16个观测脉冲轮廓示例
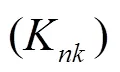
为了检验新的多成分脉冲标准轮廓在脉冲星测时过程中的应用,我们需要比较这一标准轮廓组在测时时生成的结果与使用单成分标准轮廓对脉冲星进行测时的结果。首先,将模拟观测脉冲轮廓数据对齐后叠加生成单成分的脉冲标准轮廓(对照组,如图3中点线所示);接下来,我们利用本节第一段中的方法重新生成了一组模拟脉冲轮廓,然后考察利用单成分脉冲标准轮廓与多成分脉冲轮廓分别对这一组新生成的模拟脉冲轮廓进行比对,获得这一组脉冲轮廓与两组脉冲标准轮廓之间的相位差,并将求得的相位差与生成脉冲轮廓时加入的相位移动进行对比。单成分脉冲标准轮廓测时使用的是经典的相位梯度法计算标准轮廓与模拟脉冲轮廓的相位差;多成分脉冲标准轮廓的测时稍微复杂一些,需要将标准轮廓中的多个成分以不同的线性组合方式进行叠加,并以相位梯度法计算每个叠加后的轮廓与模拟脉冲轮廓的相位差,最终保留计算误差最小的一组结果。图4中绘制的即为两种不同测时方式获得的测时结果。在图4所示的多次试验中,单辐射成分进行测时给出的相位误差的标准差为0.00653,而多辐射成分测时给出的相位误差的标准差为0.00271。显然,当脉冲轮廓中存在多种辐射成分时,使用多成分脉冲标准轮廓进行测时明显优于使用传统的单成分标准轮廓进行测时。

图3 成分分离获得的3种不同脉冲轮廓成分(即多成分脉冲标准轮廓)与单成分脉冲标准轮廓对比图

图4 分别利用单成分与多成分脉冲标准轮廓进行测时的测时残差
3 关于多成分脉冲轮廓模版获取方式的讨论
在上一节中采用了数值模拟的方式展示了多成分脉冲轮廓模版的应用,然而模拟数据与真实数据存在一定的差别,因此需要针对性地进行相应讨论。
在以上多成分脉冲轮廓分离过程的模拟中,由于事先假定了轮廓中存在3个成分,在拟合时同样采用了3成分拟合,这样才得到图3中所示的结果。在使用实际的脉冲星观测轮廓进行以上操作时,由于无法事先判断脉冲轮廓中存在几个辐射成分,需要依次对成分数进行试验,然后考察分离轮廓成分的线性相关性,然后采用分离出的所有脉冲轮廓成分的最小线性无关组作为最终的成分分离结果。
在脉冲星模式变换时,有可能会存在过渡态[14],这一状态的脉冲形状不属于任何一种稳定模式。如果存在过渡态,那么将观测数据直接折叠积分获得的脉冲轮廓可能并非是简单的多种模式的线性组合,而是有可能存在非齐次或非线性效应。此时再使用以上成分分离方法时可能导致结果有较大误差。因此,在实际的成分分离过程中,如果采用不同的脉冲轮廓组进行成分分离实验时获得了相差较大的结果,需要参考核主成分分析(kernel PCA,KPCA)[15]方法考虑成分叠加时的非线性效应后再进行成分分离。
4 结语
通过对存在多种辐射模式的脉冲星的模拟观测轮廓进行成分分离实验,发现对该类脉冲星进行测时时,使用多成分标准轮廓给出的测时结果的精度要高于单成分标准轮廓的测时结果精度。这意味着在进行脉冲星测时时,对存在多种辐射成分的脉冲星采用多成分脉冲标准轮廓是有必要的,且对于无法判断是否存在多种辐射成分的脉冲星,也有必要采用成分分离法对其轮廓是否含有多种线性无关轮廓成分进行判断,以便于获得更高精度的测时结果。
[1] HELFAND D J, MANCHESTER R N, TAYLOR J H. Observations of pulsar radio emission. III-stability of integrated profiles[J]. The Astrophysical Journal, 1975(198): 661-670.
[2] TAYLOR J H, MANCHESTER R N, HUGUENIN G R. Observations of pulsar radio emission. I-total intensity measurements of individual pulses[J]. The Astrophysical Journal, 1975(195): 513-528.
[3] BARTEL N, MORRIS D, SIEBER W, et al. The mode-switching phenomenon in pulsars[J]. The Astrophysical Journal, 1982, 258: 776-789.
[4] RANKIN J M. Toward an empirical theory of pulsar emission. III-mode changing, drifting subpulses, and pulse nulling[J]. The Astrophysical Journal, 1986(301): 901-922.
[5] REDMAN S L, WRIGHT G A E, RANKIN J M. Pulsar PSR B2303+30: a single system of drifting subpulses, moding and nulling[J]. Monthly Notices of the Royal Astronomical Society, 2005, 357(3): 859-872.
[6] WANG N, MANCHESTER R N, JOHNSTON S. Pulsar nulling and mode changing[J]. Monthly Notices of the Royal Astronomical Society, 2007, 377(3): 1383-1392.
[7] TIPPING M E, BISHOP C M. Probabilistic principal component analysis[J]. Journal of the Royal Statistical Society: Series B (Statistical Methodology), 1999, 61(3): 611-622.
[8] YIP C W. Spectral classification of quasars in the sloan digital sky survey: eigen spectra, redshift, and luminosity effects[J]. The Astronomical Journal, 2004, 128(6): 2603-2630.
[9] JARVIS M, JAIN B. Principal component analysis of PSF variation in weak lensing surveys[J/OL]. (2004-12-19)[2023-03-10]. https://arxiv.org/abs/astro-ph/0412234.
[10] DELCHAMBRE L. Weighted principal component analysis: a weighted covariance eigen decomposition approach[J]. Monthly Notices of the Royal Astronomical Society, 2015, 446(4): 3545-3555.
[11] HE J J, TAN E L, GAN W S. Time-shifted principal component analysis based cue extraction for stereo audio signals[C] // IEEE International Conference on Acoustics, Speech and Signal Processing, 2013.
[12] CHEVEIGNÉA D, SIMON JONATHAN Z. Denoising based on time-shift PCA[J]. Journal of Neuroscience Methods, 2013, 165(2): 297-305.
[13] HYVARINEN A, OJA E. Fast independent component analysis, algorithms and applications[J]. Neural Networks, 2000, 13(4-5): 411-430.
[14] SULEYMANOVA S, BILOUS A. The discovery of transitive phenomenon in the radio emission of the mode-switcher PSR B0943+10[J/OL]. (2022-10-9)[2023-03-10].https://arxiv.org/abs/2210.04215.
[15] SCHÖLKOPF B, SMOLA A, MÜLLER K R. Kernel principal component analysis[C]//International conference on artificial neural networks, Berlin, Heidelberg: Springer, 1997.
Multi-component pulse profile template and the application in pulsar timing
LU Ji-guang1,2, LIU Yu-lan1,2, JIANG Peng1,2
(1. National Astronomical Observatory, Chinese Academy of Sciences, Beijing 100101, China;2.Guizhou Radio Astronomical Observatory, Guizhou University, Guiyang 550000, China)
The mode change phenomena exist in the radio observation data of some pulsars, and the change of mean pulse profile introduces difficulties into pulsar timing. This paper introduces a scheme for decomposing the observed pulse profiles with multiple components, and shows that multi-component pulse profile template is better than single-component template in measuring the pulse arrival time.
pulsar; pulsar timing; mode switching; pulse profile template; PCA(principal component analysis)
卢吉光, 刘雨兰, 姜鹏. 多成分脉冲轮廓模版及其在脉冲星测时中的应用[J]. 时间频率学报, 2023, 46(3): 171-177.
10.13875/j.issn.1674-0637.2023-03-0171-07
2023-03-10;
2023-03-29
国家自然科学基金资助项目(12003047)

