面向脉冲星时的原子钟钟差研究
黄玉祥,李柯伽,郝龙飞,李志玄,徐永华,沈发新,汪敏,程向明,6
面向脉冲星时的原子钟钟差研究
黄玉祥1,2,3,李柯伽4,5,郝龙飞1,3,*,李志玄1,3,徐永华1,3,沈发新1,2,3,汪敏1,3,程向明1,2,3,6
(1. 中国科学院 云南天文台,昆明 650216;2. 中国科学院大学,北京 100049;3. 中国科学院 天体结构与演化重点实验室,昆明 650216;4. 北京大学 物理学院天文系,北京 100871;5. 中国科学院 国家天文台,北京 100101;6. 云南省应用天文技术工程实验室,昆明 650216)
毫秒脉冲星是宇宙中稳定的“天然时钟”。毫秒脉冲星这一特性可用于建立新的时间保持基准,通过协同原子钟的短期稳定性,形成长期稳定的脉冲星时。利用40 m射电望远镜,通过观测若干颗毫秒脉冲星,研究人员开展了脉冲星计时和脉冲星钟方面的研究。目前,已经完成了相关实验平台的搭建、原子钟之间的长期比对和钟差外推等实验,成功地将贝叶斯方法应用于钟差谱估计,初步实现了钟差信号的最优估计和外推。
毫秒脉冲星;脉冲星钟;贝叶斯估计
0 引言
脉冲星是20世纪60年代的天文学四大发现之一[1],目前普遍接受的唯象辐射模型是“旋转灯塔”模型[2]。它们最大的特点是辐射周期性脉冲,周期主要分布在几毫秒到几秒之间。其中,有一部分脉冲星的周期变化率在1×10-19到1×10-21之间,且周期小于30 ms,通常被称为毫秒脉冲星,在已发现的 3 000多颗脉冲星中约占11%[3]。它们辐射周期具有超高稳定性,故可以被用作时间信标[4]。
当前我们使用的时间基准是基于国际原子时(International Atomic Time,TAI)的衍生时标。TAI是时间权度局(Bureau International des Poids et Mesures,BIPM)[5]利用全球各地450多台原子钟的历史数据经过加权平均后通过频率基准和次级基准对自由原子时EAI进行频率校准,每月计算一次,准确度约为10-16量级。现代授时体系中,高精度时间是通过BIPM提供的事后纸面时间实现,每月一次。脉冲星时间的物理机制和地面原子钟完全不同,脉冲星时标的系统差完全独立于TAI时标系统,因此它可以提供独立的时间改正。
自从1982年第一颗毫秒脉冲星PSR B1937+21[6]被发现以来,国际上纷纷开展了利用毫秒脉冲星计时来构建脉冲星时间系统的研究。同年,J. Defter和P. Boynton[7]把频域分析方法应用到脉冲星计时噪声功率谱的研究中。1988年,B. Guinot等[8]首次提出利用脉冲星建立时间标准,开辟了该领域的相关探索。1990年,R. S. Foster和D. H. C. Backer等[9]把多颗脉冲星的计时数据应用到原子钟误差的分析中。1991年,B. Guinot及G. Petit等[10]讨论了利用脉冲星计时实现脉冲星时间标准的可行性,用BIPM时间尺度,PSR B1937+21 8年的计时精度约为4×10-15。1994年,V. M. Kaspi等[11]深入分析了脉冲星PSR B1855+09和PSR B1937+21计时结果,指出其在一年以上的相对频率稳定度可以达到10-14,与一般地方原子时的稳定度相当,使脉冲星计时检验原子时误差成为可能。1996年,G. Petit和P. Tavella[12]第一次提出了建立综合脉冲星时的意义并给出了脉冲星时加权的算法。1997年,S. M. Kopeikin应用散射噪声理论研究了计时噪声,将低频噪声进行分类[13]并在1999年建立了脉冲星低频计时噪声的统计模型[14];2004年,他[15]又研究了低频计时噪声对计时残差及其测量参数的影响和它的傅里叶分析与谱敏感性。2001年,A. N. Lommen[16]在分析上述两颗脉冲星长期计时观测数据时,发现毫秒脉冲星PSR B1855+09约15年跨度的观测数据得到脉冲星时间长期频率稳定度可优于美国海军天文台保持的原子时间基准。后来,A. E. Rodin等[17-18]研究了脉冲星时的维纳滤波算法,发现在弱红噪声条件下,该算法优于加权算法。为了更好地研究和应用毫秒脉冲星计时特性,三大独立的脉冲星计时阵从2012年起逐步建立,分别是Parkes脉冲星计时阵(Parkes Pulsar Timing Array,PPTA)[19-20]、欧洲脉冲星计时阵(European Pulsar Timing Array,EPTA)[21]和北美纳赫兹引力波天文台(North American Nanohertz Observatory for Gravitational Wave,NANOGrav)[22]。为了提高计时精度以更好地探测引力波,这三个脉冲星计时阵联合构成了国际脉冲星计时阵(International Pulsar Timing Array,IPTA)[23]。除了探测引力波,这些计时阵的数据也被用于脉冲星时间方面的研究。G. Hobbs、W. Coles和D. J. Reardon等[24-26]利用频率论思想研究了脉冲星计时阵钟差的红噪声,测量了原子时的波动并构建了脉冲星时标。2014年,K. J. Lee等[27]指出最优化脉冲星时间尺度的构建其实就是脉冲星计时噪声的测量及相关波形估计问题,并提出贝叶斯随机波形估计算法。 L. Lentati、K. J. Lee和R. N. Caballero等[28-29]把贝叶斯算法应用到脉冲星时间的问题上来,分析了计时噪声。R. Píriz和G. Hobbs等[30-31]利用贝叶斯算法,基于脉冲星计时阵构建了脉冲星时间。由于脉冲星计时阵发布数据时间间隔较长,R. Píriz和G. Hobbs等给出的事后纸面时间在较长的时间跨度上预报时间的精度会严重下降,而脉冲星钟则需要望远镜在较短的时间跨度(如一周)上定期进行计时观测以实现持续预报高精度时间。EPTA在2018年启动了“PulChron”研究项目[30],针对18颗毫秒脉冲星进行精确的计时观测,目的是为了验证脉冲星时标服务于现有原子钟系统尤其是伽利略导航时间系统的有效性和可行性。这是真正意义上的脉冲星钟项目。然而,他们构建脉冲星钟的具体算法是不公开的,国内需要独立地开展研究。
南山26 m射电望远镜于20世纪90年代开始进行脉冲星计时方面的研究,是国内最早的。通过对300余颗脉冲星的脉冲到达时间(time of arrival,TOA)进行长期监测,初步形成了自主的星历表。从2017年9月起,500 m口径球面射电望远镜(FAST)[32]逐步进行脉冲星高精度计时方面的研究,目前的结果表明,计时精度比国际平均水平高出10倍以上[33]。从21世纪初开始,中国科学院国家授时中心在脉冲星时间尺度领域取得了一些成果[34-42],此外洛南40 m望远镜也从2018年开始在L波段开展单偏振脉冲星计时观测并取得了成果。昆明40 m射电望远镜(KM 40 m)对PSR J0437-4715、PSR J1713+0747 和 PSR J1909-3744等毫秒脉冲星开展了S波段(圆极化)的计时观测,取得了初步的计时结果,PSR J0437-4715的计时精度达到500 ns左右。2019年,李志玄等[43]利用KM 40 m的脉冲星计时数据成功估计了2018年8月份前后由于本地原子钟链路切换而造成的原子钟钟差的跳变,初步验证了KM 40 m的脉冲星计时数据用于脉冲星钟构建的可行性。
本文首先介绍脉冲星钟的概念,然后叙述云南天文台开展的钟比对和钟差外推实验,最后分析和讨论实验结果,初步实现了计时用的原子钟钟差的最优估计和高精度外推。
1 脉冲星钟
脉冲星钟系统需要脉冲星计时阵,本地原子钟和相位微跃计等实现,系统框图如图1所示。图中“天线”接收到的信号经过放大和整形送到数字接收机中进行消色散、周期折叠和数据格式化存储,存储的数据通过标准的脉冲星数据处理流程形成脉冲星的TOA。由于数字接收机锁相到本地原子钟,因此TOA以本地原子钟为参考。针对多颗脉冲星的TOA可以开展本地原子钟时间和频率误差估计,其结果通过伺服器反馈到相位微跃计上,以形成低相位噪声的、融合原子钟与脉冲星数据的新的钟信号(1 PPS和10 MHz)。经过分配器缓冲后输出供外界使用。
图1 脉冲星钟系统框图
具体过程主要分成两步。第一步是构建脉冲星计时阵,获得高精度的TOA。
脉冲星计时是利用望远镜观测获取多颗计时精度较高的毫秒脉冲星发出的脉冲到达望远镜的时间,主要影响因素包括地球自转、太阳系星历表、太阳风、信号传播路径上的星际介质的色散和散射、引力波背景、脉冲星自行和脉冲星的双星效应(对于脉冲双星)等。脉冲星计时是扣除上述效应后通过脉冲到达与脉冲星相对静止的太阳系质心系(binary celestial reference system,BCRS)的相位的预报实现的,相位多项式表示为



第二步是利用计时数据对计时钟信号进行谱估计,实现钟差信号的最优估计和外推。
利用贝叶斯估计,脉冲星计时残差可以用于研究计时噪声的统计特性,如频谱,功率谱以及噪声类型等。贝叶斯参数估计把噪声模型分为3类:TOA的不确定度调制的白噪声,红噪声和色散量(dispersion measure,DM)噪声[31]。钟信号的建模是脉冲星时间溯源原子时间的基础。基于贝叶斯估计,钟信号被构建成平稳的红噪声过程,符合幂律谱,钟信号的幂律谱可表示为[31]

2 钟比对实验与分析
2.1 钟比对实验
为了进行脉冲星钟算法的研究,我们开展了两部原子钟的对比和钟差外推等试验。利用相位微跃计、高精度频率计和云南天文台现有的硬件设备,笔者搭建了测试系统,如图2所示。
试验系统由两台氢原子钟、一台频率计、一台相位微跃计及控制与采集计算机组成。频率计和相位微跃计的基本性能参数分别列于表1和表2。两台氢原子钟分别由上海天文台和俄罗斯生产,下文分别以氢钟S和氢钟R表示。
实验的目的是通过相位微跃计锁相到原子钟信号,监视锁相后信号的时间与另外一台原子钟的差异,从而理解经过相位微跃计后钟差的总噪声。具体来讲,把氢钟R的秒信号和10 MHz正弦信号注入到相位微跃计中,经过相位微跃计锁相之后,比对相位微跃计输出的秒信号和氢钟S输出的秒信号;每隔1 h采集一次二者的比对值,每次连续读取300次秒信号比对数据(10 s孔径),计算机实时记录数据采集的时间信息和秒信号的比对值。

注:氢原子钟S是上海天文台自研的,氢原子钟R是俄罗斯生产的

表1 频率计性能参数

表2 相位微跃计性能参数
2.2 实验结果与分析
在2022年9月上旬至12月下旬期间,笔者采集了100多天的原始钟差数据,如图3所示。

图3 原始钟差数据
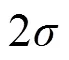

图4 扣除钟频差和钟频率导数后的钟差测量值和利用自主研发的clk_dqc软件清除钟差测量跳变后的数据
3 钟差外推实验与分析
最优波形估计是钟差外推的基础。为了构造最优波形估计器,笔者需要对数据做一次K-L分解,寻找函数的稀疏支撑空间的基。作为第一步尝试,笔者对数据进行了周期图法谱分析,对处理后的钟差数据的直接谱分析见图5(a)。数据显示出典型的红噪声特征。然而由于红噪声谱比较陡,大量的高频信号泄露到低频成分处,即谱指数被周期图法限制在≥-2的区域,因此直接周期图谱估计是有偏的,数值无法直接使用。此外,数据存在一个2.5天左右显著的周期信号和一些1天、半天等较弱的周期信号。由于两个独立运行的原子钟钟差与GPS没有关系,笔者初步分析认为1天和半天的信号是环境变化所导致的,目前尚未找到2.5天周期信号的来源。
鉴于周期图法无法直接从数据中测量红噪声谱,笔者又尝试了白化-黑化处理方法。这种方法虽然会损失信噪比,但是能够处理比-2谱指数更加陡峭的信号。针对上述的时间差数据,笔者利用标准的加窗谱分析方法[47]计算了功率谱密度,计算中使用的是Hamming窗函数。由于频率差等于时间差的时间导数,因此时间差功率谱密度可以直接转换成频率差的功率谱密度[48],计算结果见图5(b),图中展示的频差功率谱进一步验证了这个结果,频差的低频段(10-2~10-1day-1)仍旧展现出很强的红噪声。因此原始钟差的低频功率谱指数应该陡于-2。
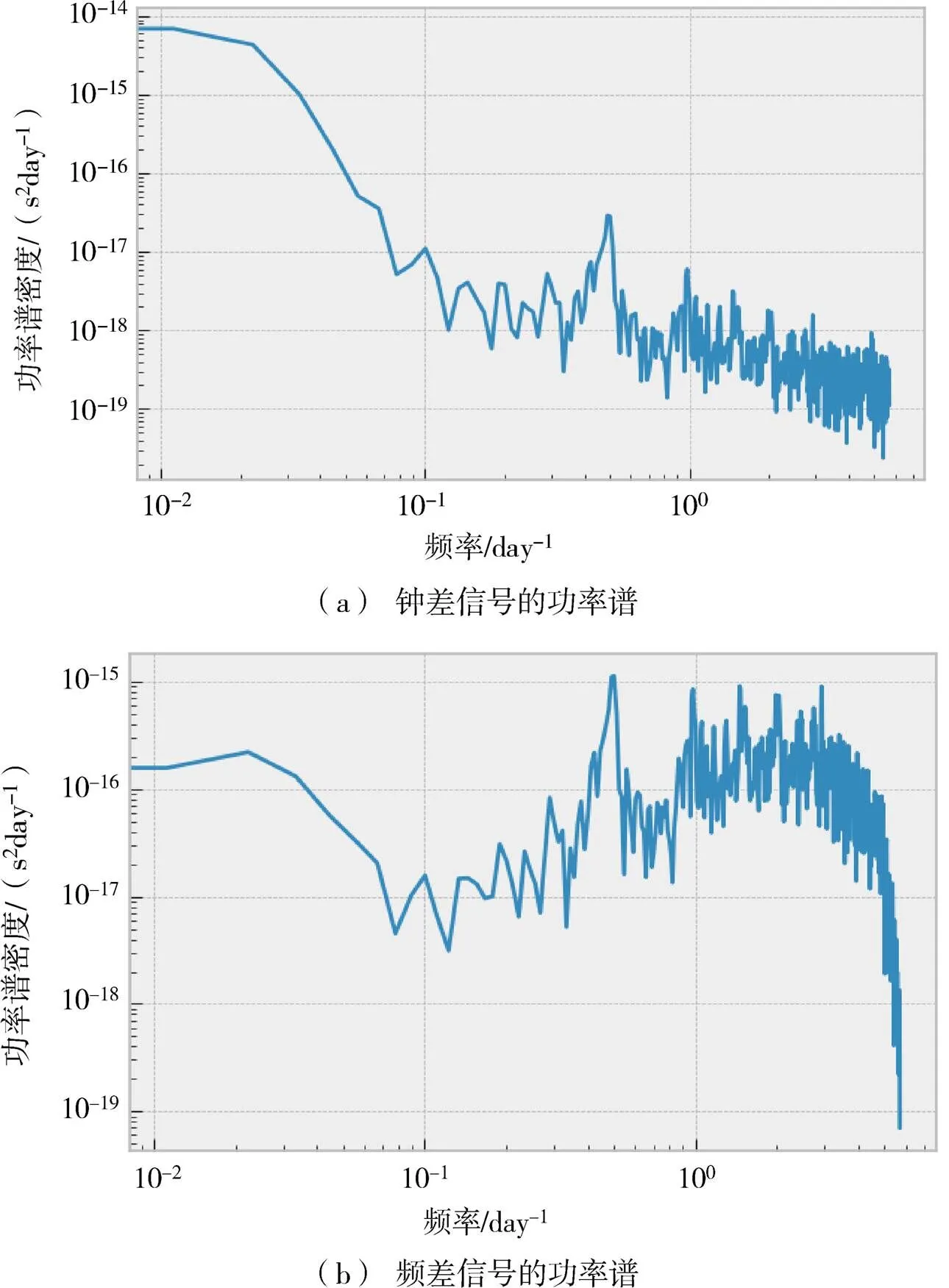
图5 钟差信号的功率谱和频差信号的功率谱
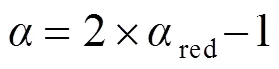

注:Efac是白噪声改正系数,Ared是红噪声的时域RMS值(对数),αred是特征谱指数
获得钟差统计模型后,笔者研究了钟差的最优估计和最优外推。X. P. Deng等[49]研究了最优外推和内插的算法,K. J. Lee等[27]给出了类似算法并得到了完整的估计误差,并证明,可以仅利用时域数据开展最优估计和外推而无需借助频域的结果,并且时域估计和维纳滤波会给出同样形式的结果。在钟差的统计模型基础上,笔者构造了针对40 m望远镜观测数据的最优估计器和外推器。应用到实测数据后的结果如图7所示。为了验证自研软件的外推能力,仅使用前半部分数据来生成最优钟差估计数据。计算结果显示,在输入数据的区间内,最优估计相对于原始测量值,大幅度降低了测量噪声,噪声水平降低了8倍左右;而在输入的数据的区间外,外推的结果和实测的结果符合很好,即在短期(数天量级,长于72 h)即使没有观测数据,仍旧可以利用统计外推器对钟进行足够精度的修正。

注:离散点是图4(b)数据中扣除线性项和二次项的结果,其中黄色部分用于最优估计器的输入数据;蓝色曲线是最优钟差估计和外推数据
4 结语
本文首先介绍了脉冲星钟的实现过程,即利用望远镜进行计时观测,获得足够的计时数据,基于贝叶斯方法研究计时噪声,建立计时钟的钟差噪声模型,最终实现保持原子钟短期稳定性的和脉冲星时间长期稳定性的脉冲星钟。然后,文章叙述了云南天文台有关脉冲星钟的研究进展:① 先导实验平台的搭建及钟差、频差自动化测量平台的搭建;② 钟差的自动测量、记录和坏数据点清除;③ 钟差的谱估计技术的探索,证实了依靠贝叶斯方法能够实现有效谱估计;④ 完成了钟差信号的最优估计和外推,实现了约8倍的噪声削减和长于72 h的数据外推预报能力。
笔者下一步将搭建脉冲星钟平台,利用上文中钟差信号的最优估计和外推算法,建立脉冲星计算时所用原子钟的钟差噪声模型,在相邻两次脉冲星计时观测之间预报未来一段时间原子钟的钟差修正值,编写伺服软件,通过伺服软件调控相位微跃计实时修正原子钟,实现脉冲星钟。
[1] HEWISH A, BELL S, PILKIGTON J, et al. Observation of a rapidly pulsating radio source[J]. Nature, 1968, 217S(130): 709-713.
[2] GOLD T. Rotating neutron stars as the origin of the pulsating radio sources[J]. Nature, 1968, 218: 731-732.
[3] MANCHESTER R N, HOBBS G B, TEOH A, et al. The Australia Telescope National Facility Pulsar Catalogue[J]. Astronomical Journal, 2005, 129(4): 1993-2006.
[4] LORIMER D R. Binary and millisecond pulsars at the new millennium[J]. Living Reviews in Relativity, 2001, 4(1): 1-5.
[5] BIPM. BIPM annual report on time activities[EB/OL]. (2021-08-14)[2023-02-12]. https://webtai.bipm.org/ftp/pub/tai/annual- reports/bipm-annual-report/annual_report_2020.pdf.
[6] BACKER D H C, KULKARNI S R, HEILES C, et al. A millisecond pulsar[J]. Nature, 1982, 300(5893): 615-618.
[7] DEFTER J, BOYNTON P. Techniques for the estimation of red power spectra I. Context and methodology[J]. The Astrophysical Journal, 1982(261): 337-350.
[8] GUINOT B, SEIDELMANN P K. Time scales-their history, definition and interpretation[J]. Astronomy and Astrophysics, 1988, 194: 304-308.
[9] FOSTER R S. Constructing a pulsar-timing array[J]. Astrophysical Journal, 1990, 361(1): 300-308.
[10] GUINOT B, Petit G. Atomic time and the rotation of pulsars[J]. Astronomy & Astrophysics, 1991, 248: 292-296.
[11] KASPI V M, TAYLOR J H, RYBA M F. High-precision timing of millisecond pulsars. III. Long-term monitoring of PSRs B1855+09 and B1937+21[J]. Astrophysical Journal, 1994, 428: 713-728.
[12] PETIT G, TAVELLA P. Pulsars and time scales[J]. Astronomy & Astrophysics, 1996, 308(1): 290-298.
[13] KOPEIKIN S M. Millisecond and binary pulsars as nature’s frequency standards. I. A generalized statistical model of low-frequency timing noise[J]. Monthly Notices of the Royal Astronomical Society, 1997, 288(1): 129-137.
[14] KOPEIKIN S M. Millisecond and binary pulsars as nature’s frequency standards. II. The effects of low-frequency timing noise on residuals and measured parameters[J]. Monthly Notices of the Royal Astronomical Society, 1999, 305(3): 563-590.
[15] KOPEIKIN S M. Millisecond and binary pulsars as nature’s frequency standards. III. Fourier analysis and spectral sensitivity of timing observations to low-frequency noise[J]. Monthly Notices of the Royal Astronomical Society, 2004, 355(2): 395-412.
[16] LOMMEN A N. Precision multi-telescope timing of millisecond pulsars: new limits on the gravitational wave background and other results from the pulsar timing array[D]. Berkeley: University of California, 2001: 20-35.
[17] RODIN A E. Optimal filters for the construction of the ensemble pulsar time[J]. Monthly Notices of the Royal Astronomical Society, 2008, 387(4): 1583-1588.
[18] RODIN A E, CHEN D. Optimal filtration and a pulsar time scale[J]. Astronomy Reports, 2011, 55(7): 622-628.
[19] MANCHESTER R N, HOBBS G, BAILES M, et al.The Parkes Pulsar Timing Array project[J]. Publications of the Astronomical Society of Australia, 2012, 30: 1-31.
[20] HOBBS G.The Parkes Pulsar Timing Array[J]. Classical and Quantum Gravity, 2013, 30(22): 224007.
[21] LENTATI L, TAYLOR S R, MINGARELLI C M, et al.European Pulsar Timing Array limits on an isotropic stochastic gravitational-wave background[J]. Monthly Notices of the Royal Astronomical Society, 2015, 453(3): 2576-2598.
[22] ARZOUMANIAN Z, BRAZIER A, BURKR S S, et al.The nanograv nine-year data set: limits on the isotropic stochastic gravitational wave background[J]. The Astrophysical Journal, 2016, 821(1): 13-23.
[23] MANCHESTER R N.The International Pulsar Timing Array[J]. Classical and Quantum Gravity, 2013, 490(22): 224010.1-12.
[24] HOBBS G, COLES W, Manchester R N, et al.Development of a pulsar-based time-scale[J]. Monthly Notices of the Royal Astronomical Society, 2012, 427(4): 2780-2787.
[25] COLES W, HOBBS G, CHAMPION D J, et al.Pulsar timing analysis in the presence of correlated noise[J]. Monthly Notices of the Royal Astronomical Society, 2011, 418(1): 561-570.
[26] REARDON D J, HOBBS G, COLES W, et al.Timing analysis for 20 millisecond pulsars in the Parkes Pulsar Timing Array[J]. Monthly Notices of the Royal Astronomical Society, 2016, 455(2): 1715-1769.
[27] LEE K J, BASSA C G, JANSSEN G H, et al.Model-based asymptotically optimal dispersion measure correction for pulsar timing[J]. Monthly Notices of the Royal Astronomical Society, 2014, 441(4): 2831-2844.
[28] LENTATI L, SHANNON R M, SOLES W A, et al.From spin noise to systematics: stochastic processes in the first International Pulsar Timing Array data release[J]. Monthly Notices of the Royal Astronomical Society, 2016, 458(2): 2161-2187.
[29] CALALLERO R N, LEE K J, LENTATI L, et al.The noise properties of 42 millisecond pulsars from the European Pulsar Timing Array and their impact on gravitational-wave searches[J]. Monthly Notices of the Royal Astronomical Society, 2016, 457(4): 4421-4440.
[30] PÍRIZ R, GARBIN E R, PEDRO K, et al.PulChron: A pulsar time scale demonstration for PNT systems[J]. Proceedings of the 50th Annual Precise Time and Time Interval Systems and Applications Meeting, Reston, 2019: 191-205.
[31] HOBBS G, GUO L, CALALLERO R N, et al.A pulsar-based time-scale from the International Pulsar Timing Array[J]. Monthly Notices of the Royal Astronomical Society, 2020, 491(4): 5951-5965.
[32] NAN R D.Five hundred meter aperture spherical radio telescope(FAST)[J]. Science in China: Physics, Mechanics and Astronomy, 2006, 49(2): 129-148.
[33] XU H, CHEN S, GUO Y, et al.Searching for the nano-hertz stochastic gravitational wave background with the Chinese Pulsar Timing Array data release I[J]. Research in Astronomy and Astrophysics, 2023, 23(7): 6157-6163.
[34] 仲崇霞, 杨廷高. 小波域中的维纳滤波在综合脉冲星时算法中的应用[J]. 物理学报, 2007, 56(10): 6157-6163.
[35] 仲崇霞, 杨廷高. 四种综合脉冲星时算法比较[J]. 天文学报, 2009, 50(4): 425-437.
[36] 杨廷高, 高玉平. 脉冲星时间尺度及其TOA预报初步分析[J]. 时间频率学报, 2012, 35(1):16-23.
[37] 朱幸芝, 陈鼎, 王娜. 脉冲星时间尺度的相关研究[J]. 宇航计测技术, 2011, 31(1): 35-40.
[38] 尹东山, 高玉平, 赵书红. 综合脉冲星时间尺度[J]. 天文学报, 2016, 57(3): 326-335.
[39] 赵成仕, 高玉平, 童明雷. 天然时钟—脉冲星时间尺度[J]. 科学(上海), 2018, 70(5): 44-47.
[40] 张哲浩, 童明雷, 赵成仕, 等. 脉冲星计时中噪声对稳定度的影响分析[J]. 时间频率学报, 2020, 43(3): 204-213.
[41] 杨廷高, 高玉平, 童明雷, 等. 综合脉冲星时研究进展[J]. 航空学报, 2023, 44(3): 54-70.
[42] 韩孟纳, 童明雷. 基于脉冲星观测的原子时波动检验研究[J]. 物理学报, 2023, 72(7): 417-425.
[43] LI Z X, LEE K J, CABALLERO R N, et al.Measuring clock jumps using pulsar timing[J]. Science in China: Series G Physics, Mechanics and Astronomy, 2020, 63(1):112-117.
[44] MISNER C W, THORNE K S, WHEELER J A.Gravitation[M]. San Francisco: W. H. Freeman and Company, 1973: 163-176.
[45] HELLINGS R W, DOWNS G S.Upper limits on the isotropic gravitational radiation background from pulsar timing analysis[J]. The Astrophysical Journal, 1983(265): L39-L42.
[46] EDWARDS R T, HOBBS G B, MANCHESTER R N.Tempo2, a new pulsar timing package-II. The timing model and precision estimates[J]. Monthly Notices of the Royal Astronomical Society, 2006, 372(4): 1549-1574.
[47] LEBEDEV V L.Random processes in electrical and mechanical systems[M]. 1961: 3-7.
[48] CHILDERS D G.Modern spectrum analysis[M]. New York: Institute of Electrical and Electronics Engineers Press, 1978: 50-61.
[49] DENG X P, COLES W, HOBBS G, et al.Optimal interpolation and prediction in pulsar timing[J]. Monthly Notices of the Royal Astronomical Society, 2012, 424(1): 244-251.
Research on atomic clock comparison for pulsar time
HUANG Yu-xiang1,2,3, LEE Ke-jia4,5, HAO Long-fei1,3,*, LI Zhi-xuan1,3, XU Yong-hua1,3, SHEN Fa-xin1,2,3, WANG Min1,3, CHENG Xiang-ming1,2,3,6
(1. Yunnan Observatories, Chinese Academy of Sciences, Kunming 650216, China;2. University of Chinese Academy of Sciences, Beijing 100049, China;3. Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, Kunming 650216, China;4. Department of Astronomy, School of Physics, Peking University, Beijing 100871, China;5.National Astronomical Observatories, Chinese Academy of Sciences, Beijing 100101, China;6. Engineering Laboratory on Applied Astronomical Technology of Yunnan, Kunming 650216, China)
Millisecond pulsars are the stable “celestial clock”. Based on the properties of millisecond pulsars, a new pulsar-based time scale can be established to maintain a long-term stable timescale. Pulsar timing and pulsar clocks are investigated with several millisecond pulsars, using the Kunming 40-meter radio telescope. We had built the experimental platform of pulsar clock and carried out experiments including comparison of atomic clocks and forecast of clock differences. The validation of the Bayesian approach in clock difference spectrum estimation was verified that is proved as an effective method for clock difference estimation and extrapolation.
millisecond pulsars; pulsar clock; Bayesian estimation
黄玉祥, 李柯伽, 郝龙飞, 等. 面向脉冲星时的原子钟钟差研究[J]. 时间频率学报, 2023, 46(3): 206-216.
10.13875/j.issn.1674-0637.2023-03-0206-11
2023-02-24;
2023-05-25;
haolongfei@ynao.ac.cn
国家SKA计划资助项目(2020SKA0120100);云南省科技厅对外科技合作专项资助项目(02003AD150010);国家重点研发计划资助项目(2022YFC2205203);国家自然科学基金资助项目(12073076;12173087;12041303;12063003)

