小学数学“图形与几何”领域素养的培育策略研究
张晓风
培养小学生初步的空间观念是小学数学教学的一个重要任务,让学生通过自己观察能反映几何知识本质特征的实物,进行操作、想象,在学习过程中形成和积累几何形体的表象,培养和发展空间观念。“图形的周长、面积与体积”板块的学习属于小学数学“图形与几何”领域,通过图形的周长、面积与体积的认识与计算,让学生在学习过程中建立空间观念、模型意识等,达到对学生图形与几何领域的素养培育。
一、基于课标要求,明确素养指向
在课标中,空间观念主要是指对空间物体或图形的形状、大小及位置关系的认识。纵向梳理图形与几何在小学数学教材中所呈现的内容:所属领域、典型模型、解题策略、价值作用。其中典型模型上分为3大部分:图形周长、面积、体积的计算。常考的题型有:基本图形周长、面积、体积计算以及不规则图形面积、体积的计算问题。找到知识间的共通点,厘清异同,建立空间观念,让学生学会建立知识之间的迁移,让教师更清晰地明确知识脉络。在解决问题的过程中,掌握图形的周长、面积和体积计算,并会根据基本的公式多样化地解决变形问题,形成空间观念。小学阶段的几何知识不但是初中阶段学习的必备基础,更在三维空间实际日常生活中有着广泛的应用。
二、基于教材,聚焦核心素养
1.教材分析
小学阶段“图形的周长、面积与体积”板块内容纵向梳理(见表1):
图形的周长、面积与体积的学习贯穿小学阶段三至六年级。小学数学教材四大学习领域之一“图形与几何”,以“认识”“探索并掌握”“解决实际问题”的形式纵向贯穿一至六年级各册教材中。其中“图形的周长、面积与体积”板块每种题型的解决都包含着一定的解题思路:明确信息与问题—找准公式与解答—类型总结。因此,我们打通小学阶段图形的周长、面积与体积相关知识点之间的联系,再进行整合规划,更有助于学生对这部分知识的掌握与运用。
2.确立素养目标
结合课标要求和教材意图,本板块目标确定为:
(1)图形的周长:结合实例认识周长,探索并掌握长方形、正方形、圆形的周长计算公式,知道三角形任意两边之和都大于第三边,能解决简单的实际问题。在探索的过程中,形成量感、几何直观、空间观念和推理意识。
(2)图形的面积:结合实例认识面积,探索并掌握长方形、正方形、平行四边形、三角形、梯形和圆形的面积计算公式,会估计不规则图形的面积,掌握长方体、正方体和圆柱的表面积的计算公式,能解决简单的实际问题。在探索的过程中,形成初步的量感、几何直观、空间观念、推理意识和空间想象能力。
(3)图形的体积:结合实例了解体积,探索并掌握长方体、正方体、圆柱、圆锥的体积计算公式,能用这些公式解决简单的实际问题。在探索的过程中,形成初步的量感、几何直观、空间观念、推理意识和空间想象能力。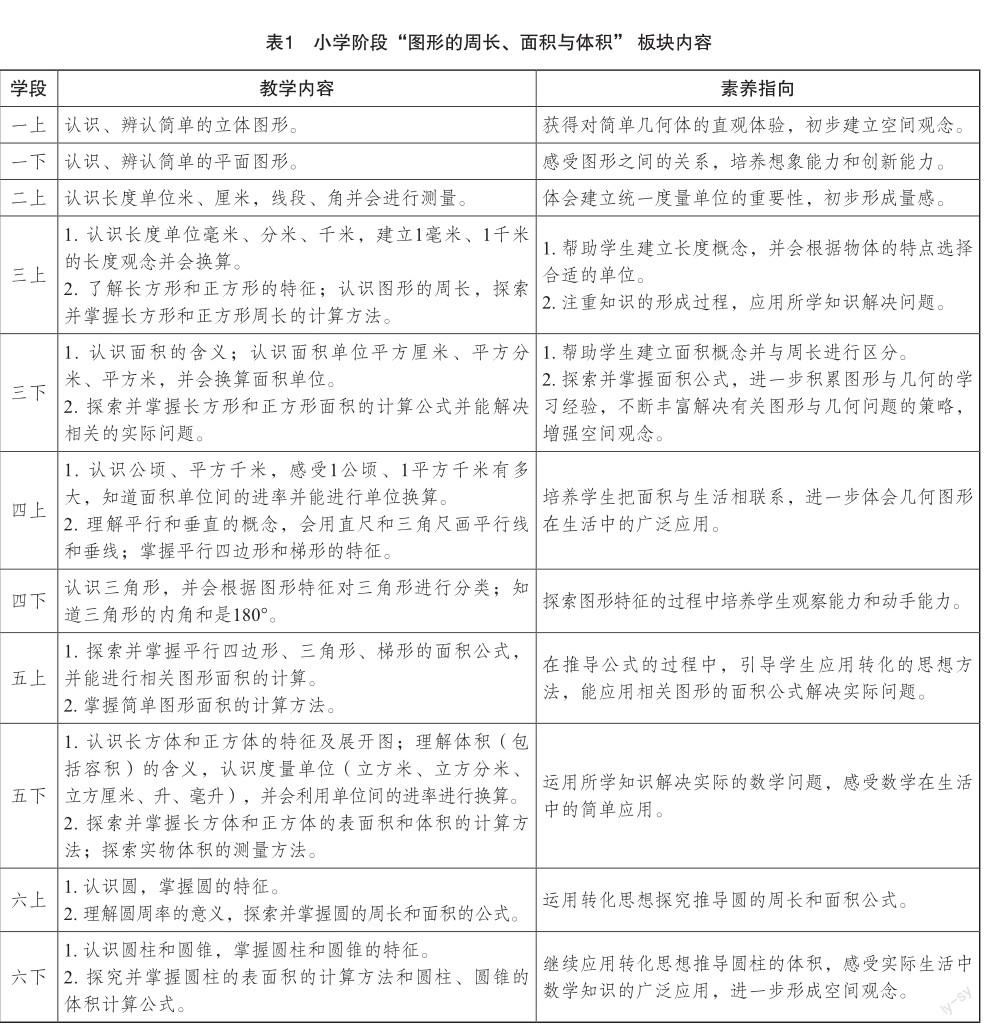
三、基于典型模型,明确解题策略
1.基本图形
(1)基本图形周长的典型例题
① 求出图形的周长:给出长方形、正方形、圆形各要素;
② 已知图形的周长,求出未知的要素(给出长方形、正方形、圆形的周长及部分要素)。注:平行四边形、三角形、梯形、半圆形的周长在教材中没有明确的课时来进行学习,但是在综合应用过程中也会根据各自的特征進行相关的考查。
(2)立体图形棱长之和的典型例题
① 求出立体图形的棱长之和(给出长方体、正方体各要素);
② 已知长方体和正方体的棱长之和,求出未知的要素(给出长方体、正方体棱长及部分要素)。
(3)基本图形面积的典型例题
① 求出图形的面积(给出长方形、正方形、平行四边形、三角形、梯形、圆形各要素);
② 已知图形的面积,求出未知要素(给出长方形、正方形、平行四边形、三角形、梯形、圆形的周长及部分要素)。
(4)立体图形表面积的典型例题
① 求出立体图形的表面积(给出长方体、正方体、圆柱各要素);
② 已知立体图形的表面积,求出未知要素(给出长方体、正方体、圆柱的表面积及部分要素)。
(5)立体图形体积的典型例题
① 求出立体图形的体积(给出长方体、正方体、圆柱、圆锥各要素);
② 已知立体图形的体积,求出未知要素(给出长方体、正方体、圆柱、圆锥的体积及部分要素)。
其中根据已知要素求出周长、面积、体积,是公式的正向应用;根据图形的周长、面积、体积与部分已知要素求未知要素,是公式的逆向应用。考查频率较高,在六年级小升初考试中综合考查情况较多。
2.不规则图形
(1)组合图形周长的典型例题
组合图形周长的典型例题:求出图形的周长(给出组合图形的各要素)。
考查频率较高,学生比较容易出错,推荐小妙招:在读清题意的情况下,再用不同颜色的笔把周长描一遍,确定求周长的线。
(2)组合图形面积的典型例题
① 求出组合图形的面积(给出组合图形的各要素);
② 求出阴影部分的面积(给出组合图形求阴影面积图形各要素)。
考查频率较高,学生比较容易出错,推荐小妙招:在读清题意的情况下,再用不同颜色的笔把面积画阴影,确定需要求面积的部分。
(3)不规则图形面积的典型例题
计算不规则叶子的面积。
这类题型因为答案的不确定性,考查频率较低,在六年级小升初考试多出现在填空题、选择题中。
(4)不规则立体图形体积的典型例题
求出不规则物体的体积(给出不规则物体放入正方体、圆柱容器内相关要素)。
在六年级小升初考试中考查情况较多。
3.图形的周长、面积与体积变形延伸
(1)图形的周长
① 长方形、正方形、圆形的各个要素分别扩大到原来的2倍,周长扩大到原来的几倍?
② 长方体、正方体的各个要素分别扩大到原来的2倍,棱长之和扩大到原来的几倍?
解决这类问题的策略是:明确信息与问题、明确解答与规律、拓展总结。各个要素分别扩大到原来的n倍,周长、棱长都扩大到原来的n倍。
(2)图形的面积
和图形的周长一样,通过数据的证明得到图形的面积的拓展总结。各个要素分别扩大到原来的n倍,面积、表面积都扩大到原来的n2倍。
(3)图形的体积
和图形的周长一样,通过数据的证明得到图形面积的拓展总结。各个要素分别扩大到原来的n倍,体积扩大到原来的n3倍。
这种类型题考查频率较高,在六年级小升初考试多出现在填空题、选择题中,学生比较容易出错,推荐小妙招:在实际计算的基础上掌握规律。
通过以上梳理,我们把图形的周长、面积和体积中的知识点串联起来,一望而知。在学习过程中真正培养了学生的空间感,从而达到图形与几何在课标中的要求。以图形的周长、面积和体积的板块梳理,从整体上把握图形的周长、面积和体积相关教学内容,明确图形的周长、面积和体积的常考题型,打通教材知识点的链接,形成解题策略,知识内容由碎片、混乱,到系统、条理,有总结、有归纳、有方法,最终构建明确的知识框架。通过板块教研教师具有了学科教学的整体观,能够有效地进行教学,学生则在体系式、综合化、深度式的学习中建立了系统的思维方式,让学科素养达成,让“双减”政策落地。
(作者单位:山东省济南市历城区礼轩小学)
责任编辑:庄 源

