狭缝高度对单色仪光谱分辨率的影响

张 靖，张 博，刘 凯，王楷炀，冯树龙，李文昊，姚雪峰

（1.中国科学院长春光学精密机械与物理研究所,吉林 长春 130033；2.中国科学院大学,北京 100049；3.长春光机科技发展有限责任公司,吉林 长春 130033）

1 引言

光栅单色仪属于典型的光栅色散型光学系统。它是精密光谱学和光谱分析中最重要的实验设备，其仪器性能会受到系统中光栅性能的影响。光谱仪器的入射狭缝高度的方向平行于光栅刻槽方向，垂直于光栅的主截面方向，且直狭缝中心高度点主光线的入射面与光栅的主截面重合，但是直狭缝边缘高度点的主光线的入射面会与光栅的主截面产生夹角，从而产生谱线弯曲。光谱系统采用离轴视场，系统谱线弯曲随着视场的增大而增大。此外，聚焦镜和准直镜的偏斜角度不当，也将加剧系统的谱线弯曲[1-2]。光栅单色仪中会设置入射和出射狭缝，从而确保光谱中很窄的一部分光照射到单像元探测器上。对光谱进行扫描，当有较大的谱线弯曲时，会导致仪器的光谱分辨率明显下降，难以满足单色仪高分辨、小型化和紧凑化的发展要求。

光谱仪器的分辨率作为表征仪器性能的重要参数指标，会对实验测试、分析结果产生很大的影响[3]。目前，对于提高光谱仪器光谱分辨率的研究主要集中在光学设计和光谱算法处理两个方向[4-6]。华中科技大学的曾延安团队基于实验室自主开发的光谱仪平台，利用修正岭估计方法建立反演模型，重建光谱立方体以改善光谱分辨率，极限条件下，光谱分辨率可改善40%以上，具有非常好的应用前景和潜力。复旦大学的陈良尧团队利用10 个1 200 线密度的光栅组成复合光栅，产生独立的光谱分区来实现200～1 000 nm 波段内0.07 nm 的光谱分辨率[7]。上述方法都有效地提高了仪器的光谱分辨率，但是耗费成本较高，实现难度较大，无法在工程上广泛应用。

光栅型光谱仪的谱线弯曲方向为长波方向[7]，为了校正由于入射狭缝高度不为零而导致的谱线弯曲，验证狭缝高度对光栅单色仪的光谱分辨率的影响程度，本文通过设置不同的狭缝高度来修正由谱线弯曲导致的光谱分辨率的下降。

2 物理模型及关系推导

由于光栅非主截面色散之间存在差异，所以光栅色散型光谱仪器存在固有的谱线弯曲[8]。基于矢量光栅方程对仪器谱线弯曲公式进行推导。其中，需考虑光栅常数、使用波长、入射狭缝高度、系统焦距等可能影响因素。

图1（a）是波长为 λ的平面波通过入射狭缝S1S2以及焦距为f1的准直物镜倾斜入射到光栅上，平面光栅刻槽平行于z轴方向，xoy坐标面与光栅主截面重合。向量代表入射平面波方向矢量，向量代表衍射平面波方向矢量。图1（b）为入射光束和衍射光束入射到主截面内的示意图。图1（c）为入射光束和衍射光束入射到非主截面内的示意图，可以得到如下形式的矢量光栅方程：

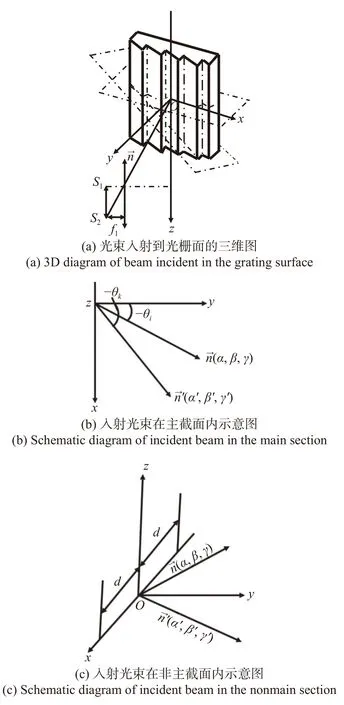
图1 光束入射到光栅的物理模型Fig.1 Physical model of the light beam incident on the grating

式中，d表示光栅槽距，λ表示入射波长，m表示光栅的衍射级次。

一般情况下，相对于主截面倾斜入射的光束在透过狭缝时会形成锥面衍射，造成谱线弯曲[7-8]。如图1（a）所示，表示入射光束和衍射光束的方向矢量，矢量值取为1，二者与主截面的夹角分别为 δ 和 δ′。倾斜入射的光线及其衍射光线在主截面的投影与y轴的夹角分别为 θi和 θk。

当入射光束和衍射光束均位于xoy坐标平面，即光栅主截面内，如图1（b）所示，则有：

沿着光栅的刻槽方向，衍射光线发生镜面反射，即；

也可表示当 δ=-δ′，平行光束倾斜主截面入射时，将入射光束和衍射光束投影在主截面内，此时入射光束与主截面的夹角 δ=0，则 cosδ=1。将其带入光栅方程中有；

化简后得到；

由式（7）可知，相对于主截面倾斜的光线被光栅偏折的角度较大，故会造成较大的谱线弯曲，且波长越长，谱线弯曲越严重[9-13]。最终谱线形成在聚焦镜的焦平面上。光线偏折角 ∆θk会使谱线沿着色散的方向移动。狭缝中心点的光线 δ=0，直入射狭缝上各点的入射角都相等，即 θi=θi0，分别将 θi、θk、θi0和 θk0带入式（7）中，相减可得式（8）；

对于小 δ 值，∆θk=θk-θk0的值很小，而且存在如下近似：

将式（9）带入式（8），可得；

谱线最终经过焦距为f′的准直透镜会聚在狭缝处，狭缝半高为，对应半角光沿着色散方向偏移的距离 ∆σ的表达式如式（12）所示：

同时，光谱线的方程式为抛物线，其曲率可以近似表示为：

将光栅方程微分，可得：

将 ∆θk代入式（14）中，可以得到由光束锥面衍射引起的沿出射狭缝高度的谱线宽度 ∆λ为

式中，∆λ 代表光线沿狭缝高度的谱线弯曲，λ代表入射光束的波长，f代表系统的焦距，h代表狭缝高度。

由式（15）可以知道，谱线弯曲会受到系统焦距、狭缝高度和波长等因素的影响。通过上式还可以知道，谱线弯曲与入射波长和狭缝高度成正比，与系统焦距成反比。增大入射狭缝高度或者缩短系统焦距都会加剧谱线弯曲，降低仪器的光谱分辨率。

3 光学系统设计

3.1 三光栅单色仪光学系统

相比于透射式系统，反射式光学系统不会产生色差，不受光谱范围的限制，可以避免系统因能量衰减而产生的谱线展宽，所以在设计时，优先考虑反射式光学系统。结合上述光学系统指标，采用非对称Czerny-Turner 型光路结构。图2 为单色仪三维和二维光路结构图，高稳定性的氙灯光源发出的复色光线经由入射狭缝，折转反射镜入射到准直物镜，经过某一角度光栅色散，获得对应波长的单色光，入射到会聚物镜。基于光栅方程，当光栅转台的转动角度范围为7.030°～76.336°时，可以覆盖185～900 nm 的光谱范围[14-21]。

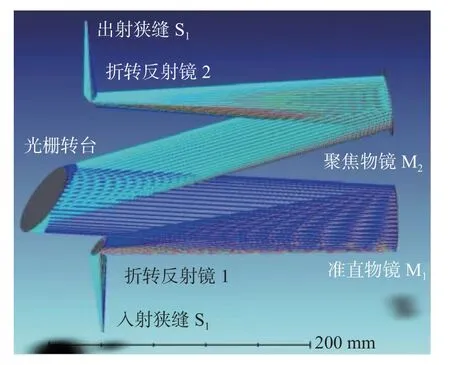
图2 单色仪光路结构图Fig.2 Optical path structure of the monochromator

图3 为单色仪的机械结构图，单色仪采用了高精度光栅转台，其电机的转角精度可以达到0.001°，以保证仪器的波长精度满足指标要求。为抑制仪器内部的杂散光，避免因能量弱造成的谱线展宽，装配时仪器内壁和夹具均做发黑处理，吸收仪器内部的漫反射光和杂散光[22-23]。

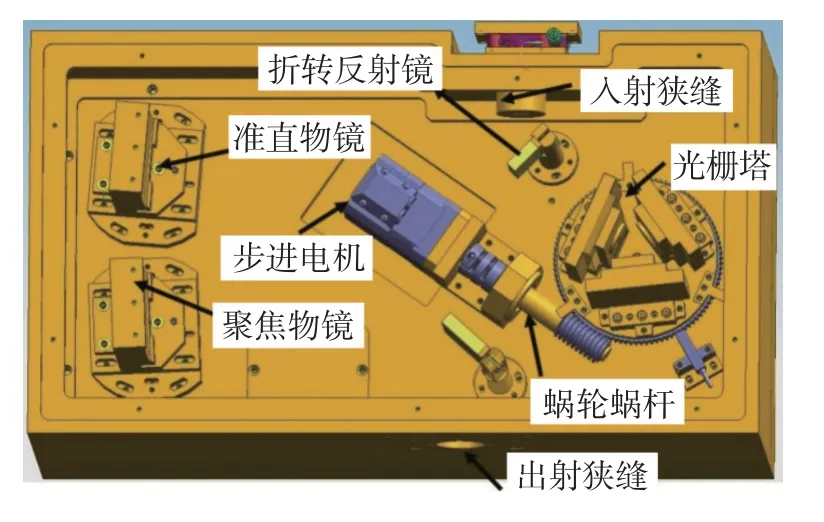
图3 单色仪机械结构图Fig.3 Mechanical structure of the monochromator

从图2～图3 中可以看出，单色仪光路之间无遮拦，视场完整。在设计时，不设置狭缝以获得尽可能大的光通量。点列图可以表征物面某点经过存在像差的光学系统后的弥散分布状态，因此以不同波长点列斑RMS 的分开程度作为标准，评价系统的光谱分辨率。图4（彩图见期刊电子版）为ZEMAX 软件中经过优化后的光路在365 nm、404 nm、435 nm、546 nm、724 nm 等波长处的点列图。箭头方向为狭缝高度方向，垂直狭缝高度为狭缝宽度方向，不同波长的光沿着狭缝宽度的方向色散。

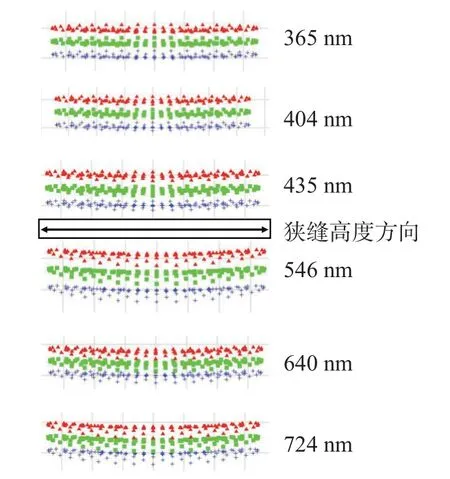
图4 不同波长处的点列图Fig.4 Point diagram at different wavelengths

图4 中不同颜色的点列斑表示不同波长光在像面会聚而成的光斑，365 nm 处的红色点列斑表示波长为364.9 nm 的光束在像面处的光斑，绿色点列斑表示波长为365 nm 的光束在像面处的光斑，蓝色点列斑表示波长为365.1 nm 的光束在像面处的光斑。可见，波长相差0.1 nm 的光在经过单色仪后完全分开，两个点斑之间不存在重叠，即不同波长的光线被完全分离。同理，波长为404 nm、435 nm、546 nm、640 nm 和724 nm 的点列斑之间也不存在重叠的情况。由此可知，单色仪在185～900 nm 波段范围内的分辨率优于0.1 nm，满足系统在全波段全视场的指标要求。同时，由点列图可以看出，随着波长的增大，谱线弯曲程度增大，系统的光谱分辨力降低。

3.2 光阑优化模拟分析

光阑可以对光学系统中的光束进行限制，将光阑片贴近狭缝时，其限制了狭缝高度上的通光量，从而改变了狭缝高度。下文通过对光阑高度进行优化，研究狭缝高度对谱线弯曲和光谱分辨率的影响。

在相同的系统参数设置下，固定狭缝宽度为10 μm，在光路中模拟不同的光阑，研究狭缝高度对谱线弯曲的影响。设置4 mm、6 mm、8 mm 和10 mm 四个不同高度的光阑，对365 nm、404 nm、435 nm、546 nm、640 nm 以及724 nm 波长的光边缘视场进行追迹，以此来表征不同光阑高度下的谱线弯曲程度，结果如表1 所示。由表1 可知，当波长一定时，光阑高度越低，谱线弯曲的程度越小，系统光谱分辨率越高；当光阑高度一定，波长越长，谱线弯曲的程度越大，系统的光谱分辨率越低。

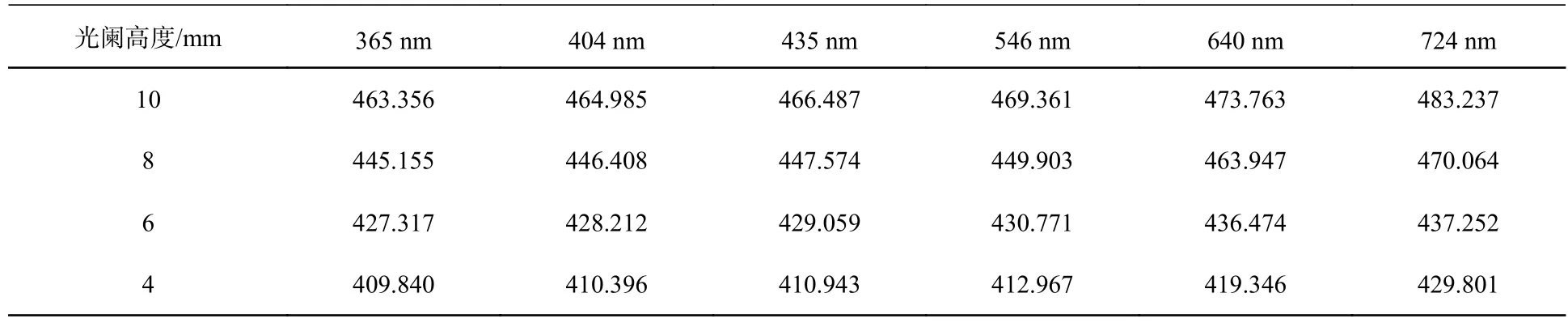
表1 不同光阑高度下边缘视场各个波长的点列斑RMS 半径值Tab.1 RMS radius of the spot array at each wavelength of the edge field-of-view under different aperture heights (μm)

4 实验验证

图5（彩图见期刊电子版）为实际装调光路后光谱分辨率的测试场景，图6 为不同高度的光阑片。

图5 测试场景图Fig.5 Test scenario diagram

图6 不同高度的光阑片Fig.6 Apertures with different heights

在测试时，将实际谱线的半高峰宽定义为仪器的光谱分辨率。选用汞灯特征波长分别为365.016 nm、404.656 nm、435.833 nm、546.075 nm、640.225 nm 以及724.511 nm 对单色仪的光谱分辨率进行测试。将汞灯固定在入射狭缝处，调整狭缝宽度为10 μm，通过在狭缝前设置高度不同的光阑片，来改变狭缝的高度。在狭缝高度分别为10 mm、8 mm、6 mm和4 mm 时，对汞灯谱线 进行扫描，结果见图7～8（彩图见期刊电子版）。

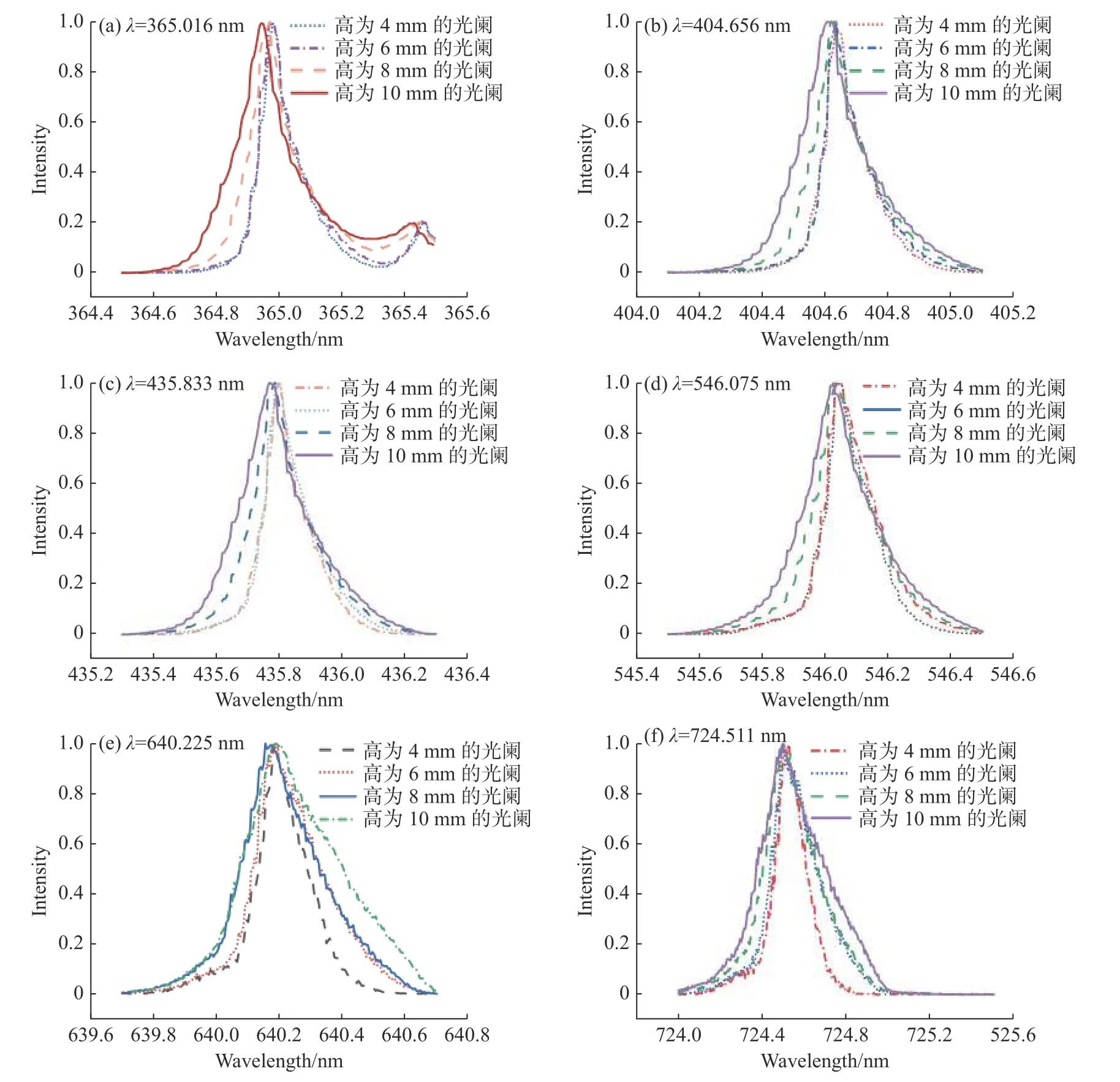
图7 不同光阑高度下，几种波长入射光的测试谱线Fig.7 Test spectral lines of mercury lamp with different wavelengthes at different aperture heights

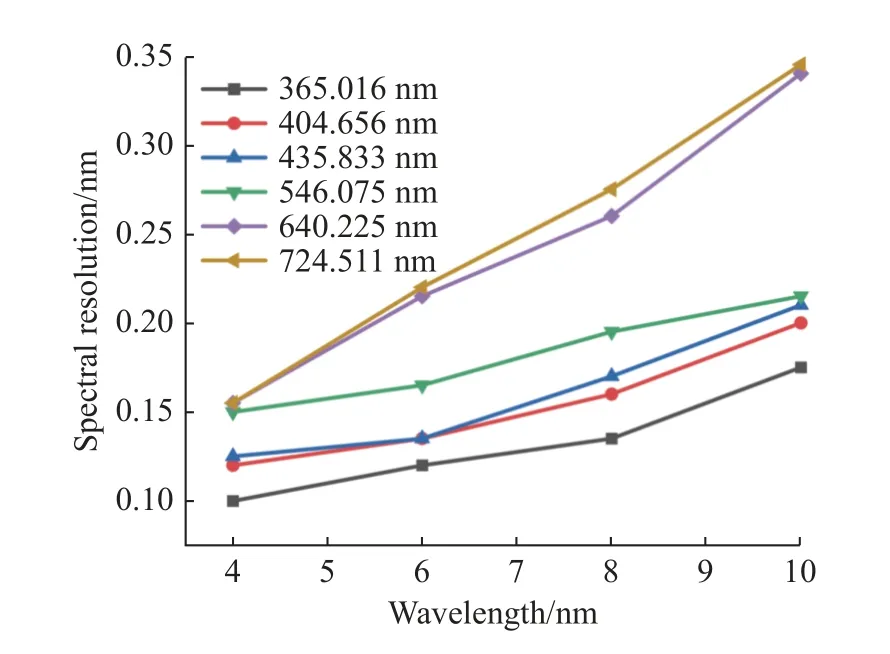
图8 不同波长和光阑高度对应的光学系统光谱分辨率Fig.8 Spectral resolution of the optical system corresponding to different wavelengths and aperture heights

从图7 可知，当入射波长λ一定时，光阑高度越小，仪器测得的汞灯谱线越尖锐，光谱分辨率越高，调整光阑高度，仪器的光谱分辨率可在0.1 nm～0.32 nm 范围内调节。同时，当光阑高度一定时，波长越长，光谱分辨率越差，由狭缝造成的谱线弯曲越严重。通过减少入射狭缝的高度可以修正光学系统的光谱分辨率，有利于提高仪器的实际性能。然而，减小狭缝高度不可避免地会导致光谱仪通光量减少，同理，减少狭缝宽度来提高光谱仪的分辨率也会导致仪器通光量减少。光谱分辨率和通光量是相互矛盾的，在实际应用中，需要针对应用场景的不同参数要求，来对二者进行权衡，以达到最佳的应用效果。

仪器实际光谱分辨率与设计结果中0.1 nm的光谱分辨率并不相符。这是因为在实际情况中，由于光栅缺陷引起的光栅衍射分辨率下降、谱线弯曲以及光学反射面的加工误差都会影响光谱仪器的分辨率，同时也会使得狭缝高度对谱线弯曲的影响不符合公式推导的情况。

5 结论

本文基于矢量光栅方程，研究了入射狭缝高度对光谱仪器谱线弯曲的影响。给出了谱线弯曲同波长、狭缝高度的解析表达式。仿真和实验验证了入射狭缝高度对Czerny-Turner 式单色仪光谱分辨率的影响。实验结果表明：降低狭缝高度，可以抑制谱线弯曲，有效优化单色仪的光谱分辨率。在此基础上，本文还提出了一种通过光阑片优化狭缝高度的方法，可以有效抑制谱线弯曲，对单色仪的光谱分辨率进行优化。发现光阑高度由10 mm 变化至4 mm 时，可以在0.1～0.32 nm范围内调节单色仪的光谱分辨率。本文研究结果对单色仪的研制和装调具有重要的理论指导作用，也为同类型仪器提高性能提供了一种新思路。