Orbital-angular-momentum spectra in coherent optical vortex beam arrays with hybrid states of polarization

YANG Ceng-hao，CHENG Ke,2 ，HUANG Hong-wei，LIAO Sai，LIANG Meng-ting，SHU Ling-yun

（1.College of Optoelectronic Engineering, Chengdu University of Information Technology,Chengdu 610225, China；2.Intelligent Manufacturing Industry Technology Research Institute, Sichuan University of Arts and Science,Dazhou 635000, China）

Abstract: Orbital-Angular-Momentum (OAM) is one of the most important parameters in high-capacity optical communication or super-resolution imaging.Based on the Huygens-Fresnel principle and the theory of coherent combination,we propose hybridly polarized vortex beam arrays in coherent combinations of radial off-axis Gaussian beamlets with vortex and polarization Topological Charges (TC).The effect of vortex,polarization and addition TC and the number of beamlets on OAM spectra of the proposed beam arrays at input and output plane are both stressed.The results show the number of beamlet and hybrid polarization present joint effect on maximal weight of OAM-modes.An increase of maximal weight value at OAM-mode is accompanied by the growing number of the beamlet,while the hybrid polarization can not significantly increase the maximum weight of OAM spectra.As the number of beamlets increases,hybrid polarization can't significantly improve the maximal weight value in OAM spectra.Furthermore,the maximal mode equals the total TC at central Optical Vortex (OV) and it is irrelevant to the number of beamlets.Whereas for other modes for non-zero weight,their locations are jointly determined by vortex,polarization and addition TCs and the number of beamlets.This work may provide potential applications in the OAM-based communication and polarization imaging technologies.

Key words: orbital angular momentum spectrum;polarization;vortex

1 Introduction

Vortex beams with helical wavefronts characterized by an azimuthal phasel(namely,vortex topological charge),e.g.Laguerre-Gaussian modes,can carry Orbital-Angular-Momentum (OAM) equivalent toper photon (being reduced-Plank constant)[1,2],which have stimulated considerable enthusiasm in optical communication,optical micromanipulation and super-resolution imaging[3-8].Vector optical fields with hybrid states of polarization can be described by hybrid morphology with linear,circular and elliptical polarizations,and their propagations in uniaxial crystal were first studied by Milioneetal..in 2010[9].Since then,many different types of hybridly polarized beams have been proposed due to their tunabilities in degree of freedom of optical polarization.For example,Guetal..investigated polarization evolution of three types of hybridly polarized beams in focal region[10],and studied the polarization rotation in a uniaxial crystal from theory to experiment[11].The hybridly polarized beams with polarization topological charges were given by Chenetal..,and used to explore spinto-orbital angular momentum conversion in nearfield zone[12].

On the other hand,high-dimension or high-purity OAM spectra can be produced by the superposition of vortex beams,shape-tailored metasurfaces,a binary array of pinhole and nanosieves[13-18].Especially,Jinetal..have reported multiplexed OAMs produced by a compact phyllotaxis nanosieve.However,the effect of hybrid polarization in coherent combination on OAM-modes has not been dealt with.Can the hybridly polarized vortex beam arrays in coherent combination present pure or multiple OAM modes,and their modes can be located by mathematical method? The motivation of the present work is to explore the relation between the maximal mode of OAM spectra and total Topological Charge (TC) of central Optical Vortex (OV),and find the mathematical equations for locations of non-zero weights for all OAM-modes.The results obtained in this paper stress the effect of polarization TCs on locations of OAM-modes,which may be useful for high-capacity optical communication or super-resolution imaging.

2 OAM spectra of hybridly polarized vortex beam arrays in coherent combination

Taking the direction ofzaxis as the beam propagation direction,the electric field of a single Gaussian beam with vortex and polarization TCs at the input plane ofz=0 in the cylindrical coordinate system is expressed as[12,19]

wherer0=(r0,φ0) is the position vectors withr0andφ0being radial and azimuthal coordinates atz=0,mdenotes polarization TC related to hybrid state of polarization of optical field,θis the angle between polarization and radial direction,δis phase retardation angle between thex0andy0components withx0=r0cosφ0andy0=r0sinφ0,exandeyare the unit vector alongx0andy0axes,respectively.The profiles of the Gaussian beamG(r0) and vortex coreV(r0) in Eq.(1) are described by

withw0andlbeing waist width and vortex TC,respectively.From the Eqs.(1) and (2),one can see that the phase factor of electric field reduces to exp[i(m+l)φ0] for the case ofm=l,which indicates that the total TC is equal to the sum of vortex and polarization TCs,i.e.TC=m+l,at input plane ofz=0.If phase retardation angleδ=0,the polarization state of optical field is linear polarization along different directions,and the optical field ofm=1 can be reduced to radially or azimuthally polarized beams forθ=0 orθ=π/2,respectively.If polarization TCm=0,the polarization of optical field is not hybrid morphology,but uniformly linear,circular or elliptical polarization states.

To elucidate the OAM spectrum of beam arrays in coherent combination,we assume that it is formed withNidentical off-axis beamlets with offaxis distance vectorrj.The optical field of the coherent beam arrays can be written by[20]

where the inputjth off-axis beamletEj(r0,0)=E(r0-rj,0)exp(iϕj) with additional phase ofϕj=2πjη/N(ηis additional topological charge) and the displacement vectorrj=(ρcosθj,ρsinθj) with radiusρ.The propagation of the resulting beam arrays at thezplane is given as

wherer=(r,φ) is the position vectors at the output plane ofzandkis the wave number.

The weightRnrepresents the relative energy ofnth OAM mode for the optical field,and its value can be calculated by

with the power of OAM spectrumPnand the expansion coefficient

Eqs.(1)-(6) provide powerful ways to solve the relative power or weight ofnth OAM mode of the resulting beam arrays,where each beamlet carries vortex and polarization TCs.Although there exist thex-andy-direction polarizations of the resulting beam arrays,their OAM spectra are identical with thexandydirections in the free space.For paraxial beams,the relation among topological chargel,nmode of OAM spectra and the weightRncan be described by[19,21]

On the other hand,the longitudinal OAM density also provide different perspectives in the evolution of OAM,and its expression is described by[22]

whereωis the circular frequency,ε0is the electric permittivity of a vacuum.The longitudinal OAM densities show consistency with the OAM spectra,and the relations is given by

In the following numerical calculationsλ=632.8 nm,w0=1 mm,θ=π/4,δ=7π/8 and Rayleigh lengthze=kw02/2 are fixed unless otherwise stated.

2.1 OAM spectra at input plane

Fig.1 (color online) gives the OAM spectra,phases and polarization states for a single Gaussian beam with vortex and polarization TCs.It is wellknown that the OAM spectrum concentrate atn=lfor non-polarization or uniform polarization[19]in Figs.1 (a),1 (d),1 (g).However,the OAM spectra concentrate atn=l±min equal weight with vortex and polarization TCs atz=0 as shown in Figs.1 (g)-1 (i).The embedded polarization TC results in the split of OAM mode.It is clear that total TCs equall+mdue to spiral phase distributions in Figs.1 (a)-1 (c),and their hybrid states of polarization improve with an increase of polarization TCs in Figs.1 (d)-1 (f).Although the phases,polarization states and OAM spectra in a single vectorial optical fields are induced by polarization TC at the input plane,the relation of Eq.(7) still holds.For example,the power weights are both 0.5 and 0.5 at OAM-modes ofn=0 and 4 for the case of (l,m)=(2,2) in Fig.1(i),respectively,but its spiral phase demonstrates the value of TC=4 as shown in Fig.1(c).

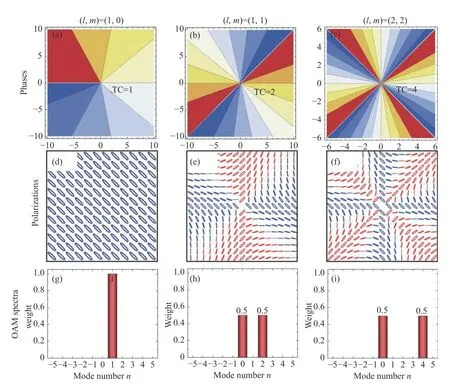
Fig.1 Phases,polarization states and OAM spectra of a single Gaussian beam with different vortex and polarization topological charges.(a),(d),(g): (l,m)=(1,0);(b),(e),(h): (l,m)=(1,1);(c),(f),(i): (l,m)=(2,2).(d),(e),(f): RH (Red) and LH (Blue) elliptical polarizations

Fig.2 (color online) shows the OAM spectra and OAM densities of beam arrays in coherent combinations with radial,rectangular and linear symmetries atz=0,where the off-axis distances of each beamlet are also marked in Figs.2 (a)-(c) and the additional topological charges are set asη=0.Comparing with the OAM-modes centered atn=0 and 2 of a single beam in Fig.1(h),the weight values decrease fromRn=0=0.5 to 0.333 and fromRn=2=0.5 to 0.09 in Fig.2(d).Although the relative power at mode ofn=0 and 2 are suppressed,more modes appear for radial beam arrays.The maximal weigh is also found all atn=0 of OAM-mode for radial,rectangular and linear symmetries,which is due to the fact that the topological charge of central optical vortices (i.e.,optical vortices at original) is zero even though there exist more non-zero vortex in the field cross section.A larger weight value at mode means that it carries more harmonic energy at this mode.The maximal weights of OAM spectra of the proposed beam arrays for different symmetry and beamlet numbers are listed in Tab.1.As one can see,the OAM-spectra in radial symmetry present more concentrated modes than those in rectangular and linear symmetries,which means that the radial symmetry may possess relative high-quality spectra.The possible physical explanation seems to be that radial symmetry is helpful to form the expected vortex or spiral structures.

Tab.1 The maximal weights of OAM spectra of the proposed beam arrays for different symmetry and beamlet numbers,the other parameters are the same as in Fig.2

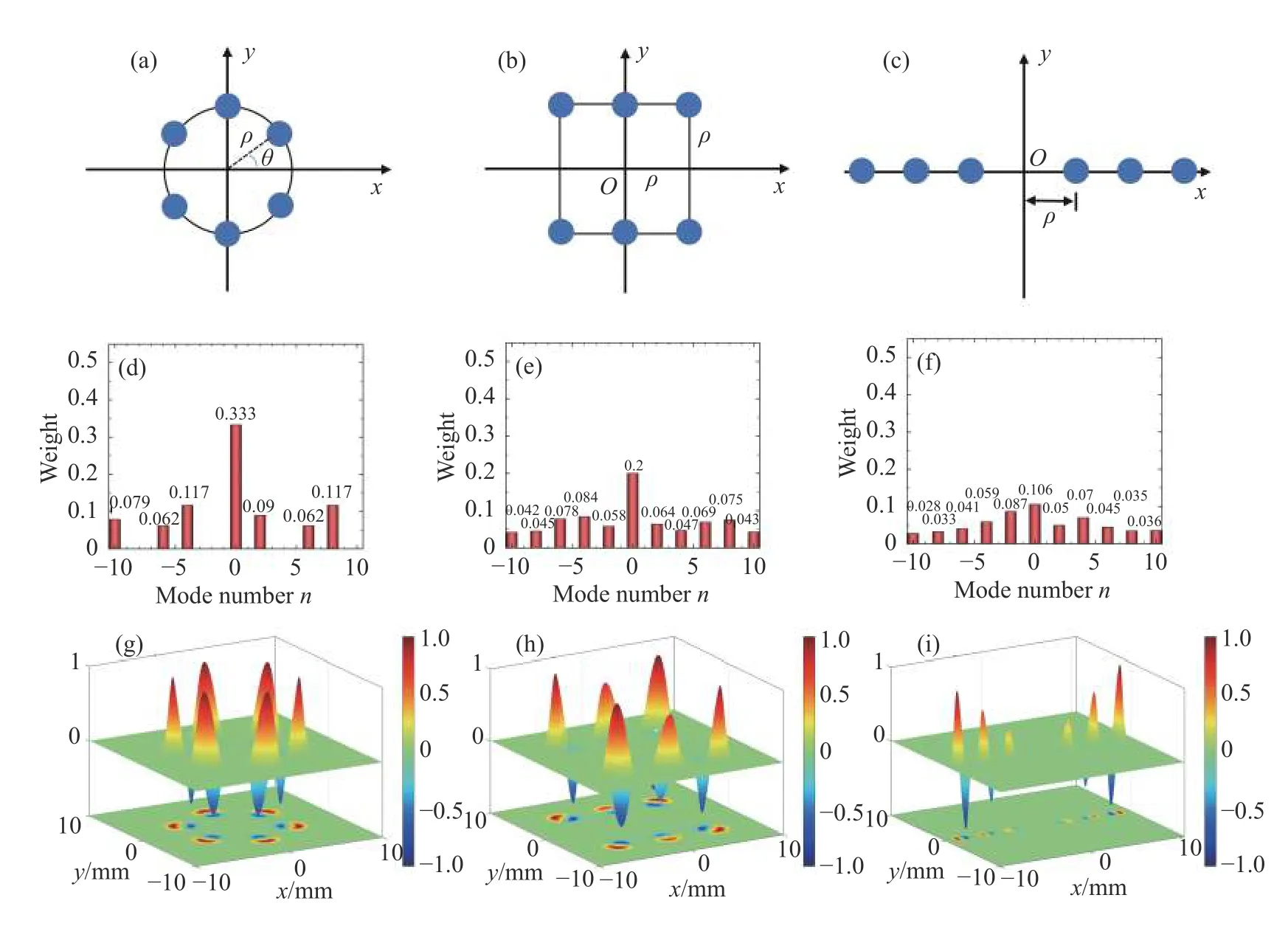
Fig.2 The OAM spectra (d)-(f) and OAM densities (g)-(i) of beam arrays in coherent combinations with radial,rectangular and linear symmetries at z=0.(a),(d),(g): radial symmetry;(b),(e),(h): rectangular symmetry;(c),(f),(i): linear symmetry.The parameters are (l,m)=(1,1),η=0,N=6 and ρ=5w0

2.2 OAM spectra at output plane

Next,our attention is paid to the dependence of OAM-spectra in coherent combination with radial symmetry on vortex and polarization TCs (l,m),additional TCηand the number of beamletNat the output plane.Radial beam arrays formed byNidentical off-axis beamlets are depicted in Fig.3 (a)(color online),where each beamlet at input plane has different initial phase,i.e.,η≠0.There may exist spiral phase of central optical vortex at (0,0,z),e.g.TC=+1,as shown in Fig.3 (b) (color online).The OAM spectra of the corresponding beam arrays are presented in Fig.3 (c) (color online),where the weight valueRn=1=0.92 at the maximal moden=1.It raises the questions of whether there exist a correlation between maximal mode and central OV,and what factors determine the topological charges of central OV.

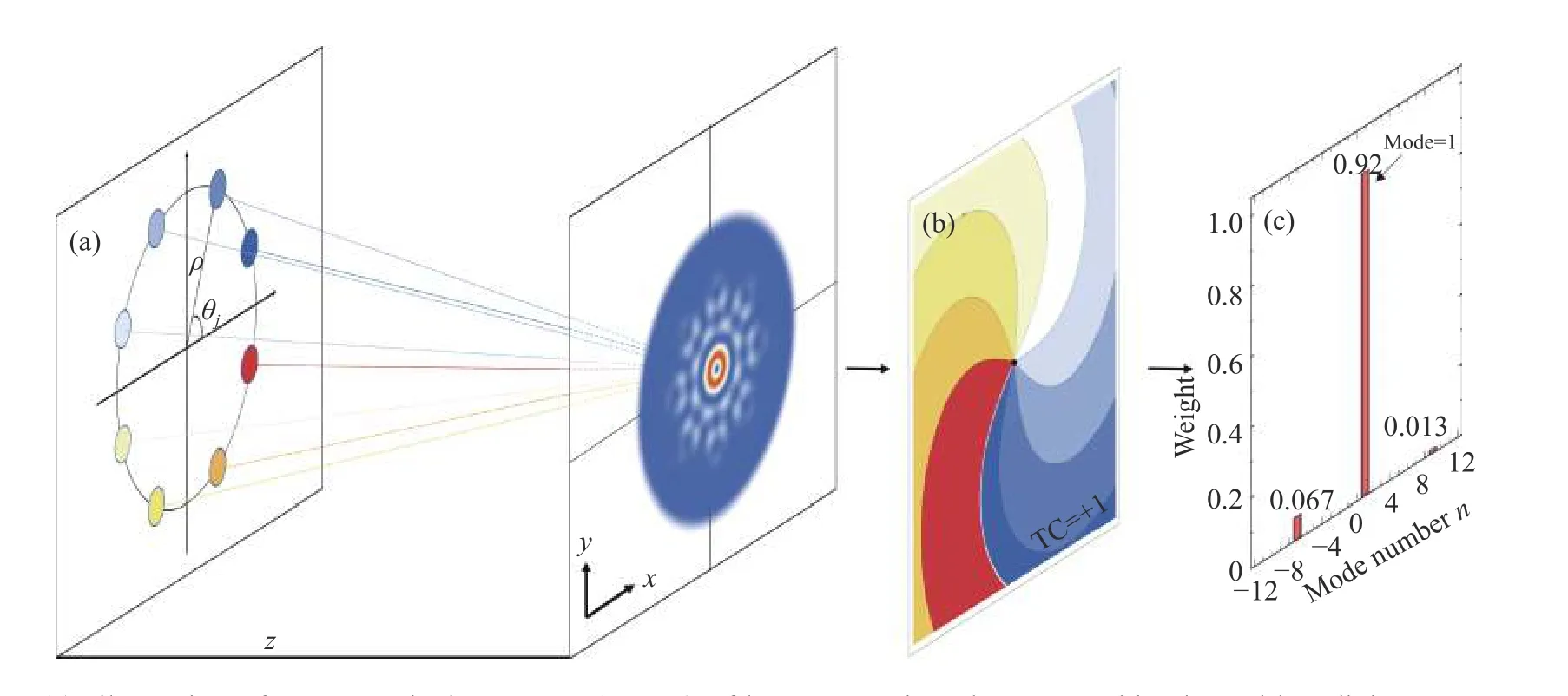
Fig.3 (a) Illustration of center optical vortex at (0,0,z) of beam array in coherent combination with radial symmetry at the output plane.(b) Spiral phase of center optical vortex.(c) OAM-spectra of the corresponding beam arrays.The parameters are (l,m)=(0,0),η=+1,N=8 and ρ=5w0

Fig.4 (color online) further gives the correspondence between the topological charge of central OV and maximal modes of OAM-spectra for differentl,m,ηatz=10ze.It is seen that the maximal mode of OAM-spectra presents a consistent one-toone match with topological charge of central OVs,which also mean that the resulting beam arrays possess a maximal spiral harmonic power at central origin (0,0,z).For example,the spiral phase circulating around origin of coordinates 4π in counterclockwise stand for the topological charge of TC=+2 as shown in Fig.4 (a),then its weight of maximal mode just locating atn=2 isRn=2=0.383.As shown in Fig.4,the values of TC of central OVs arel+η-mforl+η≥0,while forl+η˂0,the values of TC equall+η+m.It indicates that maximal modes of OAMspectra carrying maximal spiral harmonic powers are determined by the joint influence of vortex,polarization and additional topological charges ofl,mandη.Ifl+η≥0,the position of maximal mode isnmax=l+η-m,whereas it isnmax=l+η+mifl+η˂0.For example,for the case ofm=1 andm=2 in Figs.4 (c)and 4 (g),the values of TC are -1 and -2 for (l,η)=(1,-1),and their locations of maximal modes arenmax=-1 and -2,respectively.However,for (l,η)=(0,-2),the locations are -1 and 0 in Figs.4 (d) and 4 (h),respectively.It should be pointed out that there are plenty of optical vortices appearing at other areas,but only central OVs and maximal modes have clear correspondence.

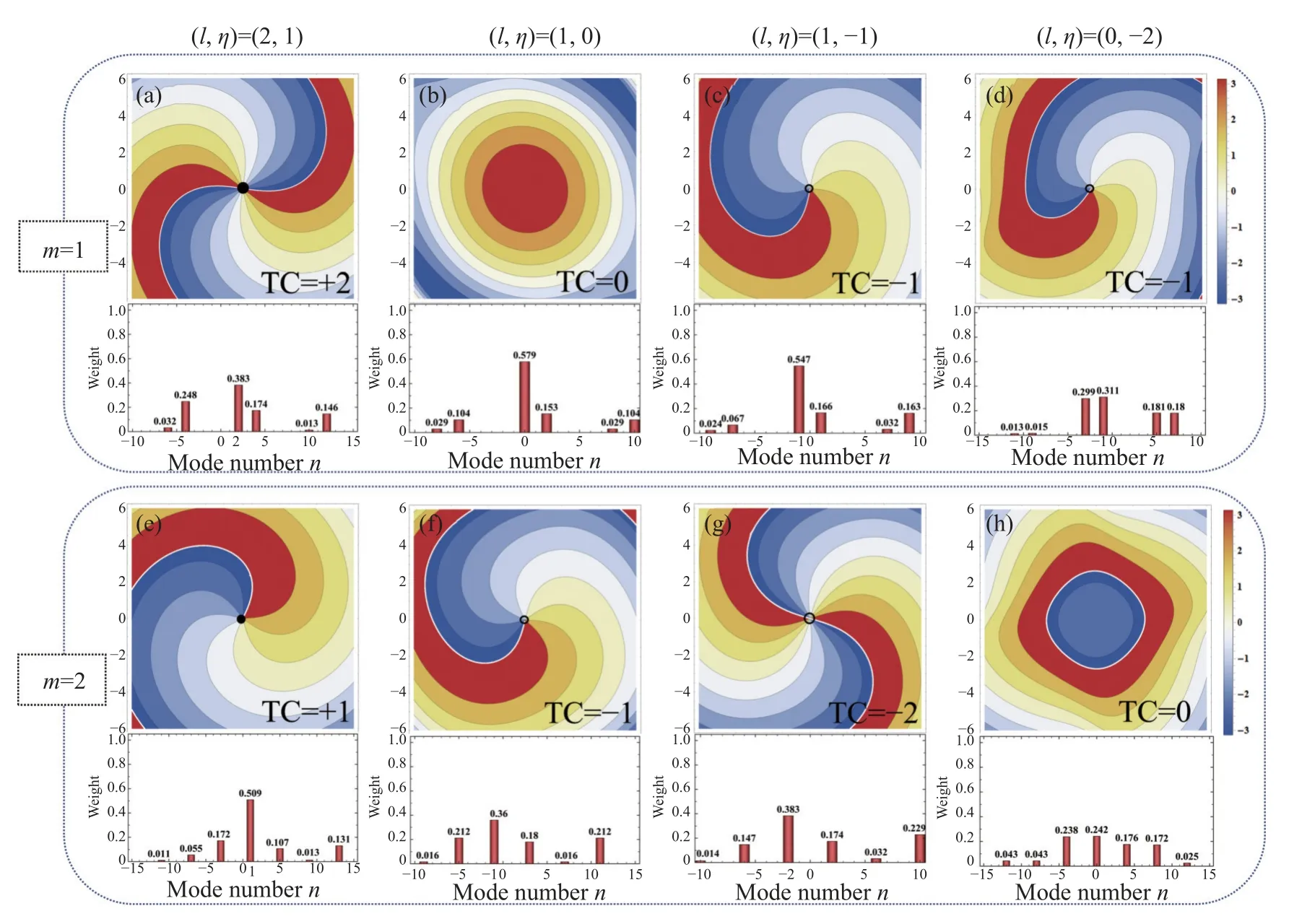
Fig.4 The correspondence between the topological charge of central optical vortex and maximal modes of OAM-spectra for different l,m,η at z=10ze.(a)-(d): m=1;(e)-(h): m=2.The parameters are N=8 and ρ=3w0

Fig.5 (color online) shows OAM-spectra,spiral phases of central optical vortex and OAM densities for differentηatz=10ze,where each beamlet at input plane possesses vortex and polarization TC of(l,m)=(1,1).Similarly,it is found that the maximal weight of OAM spectra are centered atn=-2,-1,1 and 2 because their locations are also determined bynmax=l+η+mforl+η˂0 as shown in Fig.5 (a).The OAM densities of beam arrays also evolve from independent side-lobes at input plane into kaleidoscope structures in far zone ofz=10zedue to optical interference.The positive or negative values of OAM densities at central zones marked by dotted lines in Fig.5 (c) agrees well with the positive or negative sign of central OVs,respectively.

Fig.5 OAM-spectra,spiral phases of central optical vortex and OAM densities for different η.η=-2,η=-1,η=1,and η=2 respectively,from top to bottom.The parameters are (l,m)=(1,1),N=8,ρ=3w0 and z=10ze

Now that the location of maximal mode isnmax=l+η±m,the question to raise is what happens for its maximal weight if the sum ofl+ηis fixed.Fig.6 (color online) shows the effect of polarization TCs and the number of beamlet on weight of maximal mode in OAM-spectra for a fixedl+η=2,wherem=0,1 and 2 are marked by black,red and blue lines,respectively.An increase of weight value at maximal mode is accompanied by the growing number of the beamlet,and a largerηcan make larger weights.In addition,the polarization and the number of beamlet have a combined effect in maximal weight of OAM-modes.The increase of weight value in non-polarization (i.e.m=0) is more rapid than those form=1 andm=2 with the increase ofNas shown in the shaded area in Fig.6 (a).For example,forN=7 and 12 in Fig.6 (b) the weight improves from 0.348 to 0.917 form=0,whereas form=2 it only changes from 0.516 to 0.769,respectively.The results indicate that the high-purity or high-weight OAM may be obtained by increasingNor decreasingmfor a fixedl+η.

Fig.6 (a) Effect of polarization topological charges and the number of beamlets on weight of maximal mode in OAM-spectra for a fixed l+η=2.(b) The corresponding weight in OAM-spectra for (l,η)=(2,0).The other parameters are the same as in Fig.5

Fig.7 (color online) shows the locations of OAM-modes with an increase of the number of beamletNfor differentl,ηandm,where all nonzero modes are given.Their locations of OAMmodes gradually decrease with the growing number of beamlets,which also means that the powers at other modes disappear and transfer to a few modes.More importantly,the locations of all OAM-modes for the hybridly polarized vortex beam arrays satisfy the mode equation ofn=l+η±m-αNwith arbitrary integerα(see Appendix).Ifα=0,the mode reduces ton=l+η±mcorresponding to the case of maximal modes.For example,based on the mode equation,their locations forN=10 and (l,η,m)=(1,0,1)should are -10,-8,0,2,10 and 12 ifα=1,0 and -1,respectively,then their modes are exactly presented as shown in Fig.7 (a).Despite their locations are plentiful,higher modes,e.g.,n=-20,-18,20 and 22 atα=2 and -2,are omitted due to their extremely weak weights.These locations at other cases can be obtained by using the same method.

Fig.7 Locations of non-zero weight for OAM-modes with an increasing of the number of beamlet N for different l,η and m.(a): (l,η,m)=(1,0,1),(b): (l,η,m)=(2,0,1),(c): (l,η,m)=(1,0,2),(d): (l,η,m)=(1,-2,1)

3 Conclusion

Hybridly polarized vortex beam arrays are proposed by the coherent combinations ofNidentical off-axis Gaussian beamlets with vortex and polarization topological charges,and used to explore the effect of vortex,polarization and addition topological charges (l,m,η) and the number of beamletsNon their OAM spectra.Generally,for a single beam its OAM spectrum can be induced by polarization TC,and its mode appears atn=l±min equal weights.However the proposed radial beam arrays present a greater concentration modes than those of rectangular and linear symmetries,which suggests that the radial beam arrays have an advantage in high-purity OAM spectra.The polarization and the number of beamlet have a combined effect on maximal weight of OAM-modes.An increase of the number of beamlets can lead to the increase of weight value at maximal mode.The hybrid polarizations caused by the embedded polarization TC not only damage the symmetry of OAM spectra,but also decrease its weight or purity at maximal modes.The maximal mode for the proposed beam arrays is equal to the total topological charge at center optical vortex,and its location is determined bynmax=l+η±mirrelevant to the number of beamlets.Whereas for other modes their locations appear atn=l+η±m-αNin connection with the number of beamlet.The proposed hybridly polarized vortex beam arrays provide potential applications in the high-capacity OAM-based communication or super-resolution imaging.

Appendix: Theoretical derivation of other non-zero OAM mode locations

According to Ref.[13],in the scalar field one can obtain the expansion coefficient inxory-direction

For simplicity,Eq.(A1) can be rewritten by lettingθ=0 and using Euler function as

with

Due to the fact that each beamlet possesses the same optical fields for the radial array structures,Eq.(A3) can be expanded by using integral substitution method

One can consider this geometric sequence in Eq.(A4),and find it expressed as

Only whenl+η±m-n=αNwith arbitrary integerα,which indicates that the weights of those OAMspectra are not zero,i.e.,a±≠0,only forn=l+η±m-αN.It should be point out that the location equation is only valid for radial array,but not applicable for the cases of rectangular and linear symmetries.